航天器中精密器件布局的保结构优化*

蒋睿嵩，徐萌波，张 帆，胡伟鹏，邓子辰

（1.四川大学 空天科学与工程学院，成都 610065；2.西安理工大学 土木建筑工程学院，西安 710048；3.西北工业大学 力学与土木建筑学院，西安 710129）

（我刊编委邓子辰来稿）

引 言

航天器在穿过（飞离和再入）大气层、受到空间碎片撞击[1]等过程中，航天器结构将呈现复杂的动力学行为，严重影响搭载在航天器上的精密器件的稳定性和工作精度，甚至会导致精密仪器失效，以致航天任务失败.因此，如何确保航天器上搭载的精密仪器在极端环境（包括冲击载荷等）中的工作性能是航天器设计中的重要内容之一.

当前的航天器中搭载的精密器件常被集中封装（如图1所示）.集中封装后，在航天器中选择适当的位置（需要考虑温度环境、湿度环境、动力学环境、人机环境等因素）进行安装固定[2-3].在封装后的安装位置选择过程中，无法再对精密器件的布局进行优化，这一局限性导致封装后的精密仪器安装在航天器某一动力学环境相对安全的位置后，封装薄板（upper/lower bearing plate）上仍然会存在局部共振区，局部共振区的存在对布置在共振区内的精密器件稳定性和精度影响显著.因此，合理的设计过程应当是：首先，选择封装后的精密器件安装位置；然后，以选择的安装位置的最不利载荷组合作为设计载荷依据，分析粘接有精密器件的封装薄板的动力学特性，对精密器件在封装空间中的布局进行优化设计.

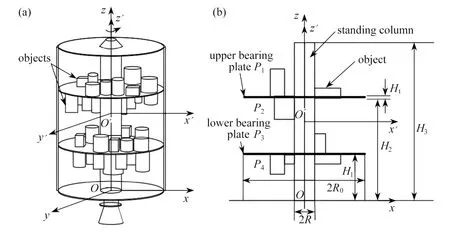
图1 航天器中电子元器件封装示意图[2]：(a) 三维模型；(b) 剖面图Fig.1 The layout sketch of capsuled electron components in a spacecraft[2]:(a) the 3D model;(b) the profile

上述布局优化设计工作最核心的难点是粘接有精密器件的封装薄板的动力学特性分析.与传统的柔性薄板振动分析不同的是，粘接有精密器件的柔性薄板厚度是非均匀的（薄板厚度可以描述成平面位置的非光滑函数），这为动力学模型的求解带来了巨大困难.

厚度非均匀薄板动力学分析也一直是动力学领域的热点问题.其中具有代表性的工作包括：Rumerman[4]给出了带肋薄板强迫振动问题的一个通解；Orrenius 和Finnveden[5]发展了有限元方法分析带肋加劲板中的波传播问题；Ichchou 等[6-7]较为系统地分析了带肋板中波传播规律，得到了一系列有意义的结果.作为影响精密器件稳定性和精度的重要因素，封装薄板局部共振问题属于该系统的局部动力学性质.近年来基于辛几何理论[8-10]发展起来的保结构方法[11-12]已被证实是精确捕捉动力学系统局部性质的有效手段[13-15]，这些成果为解决封装薄板局部共振问题提供了重要参考.因此，本文将首先发展保结构方法分析粘接精密器件的封装薄板局部共振问题；随后，基于共振特性分析结果，考虑精密器件几何尺寸、散热要求等约束条件，对精密器件在封装薄板上的布局进行优化设计，为航天器中精密器件布局设计提供参考.

1 粘接精密器件柔性封装薄板的简化动力学模型

为方便后续动力学建模及优化设计，引入如下假设：① 忽略封装薄板的阻尼耗散效应；② 假定精密器件材料参数与封装薄板相同；③ 假定封装薄板上粘接布置有n个精密器件，第i个器件布置位置用该器件与封装薄板接触面 Ωi描述，如图2所示.

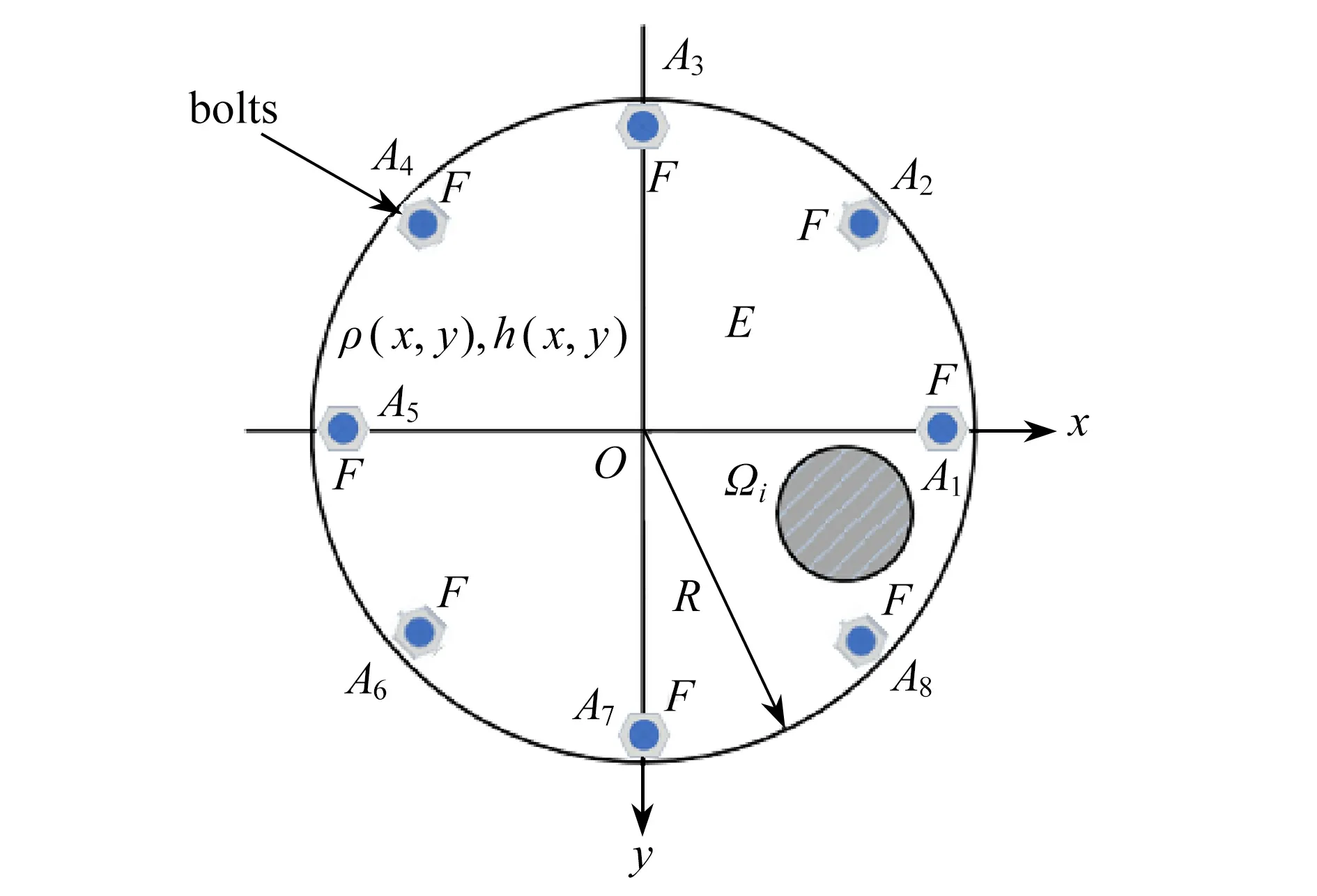
图2 精密器件与柔性封装薄板简化耦合模型Fig.2 The simplified dynamic model of the flexible panel assembled with precision devices

在上述假设前提下，考虑薄板振动变形能和振动动能，Lagrange 函数可表述为

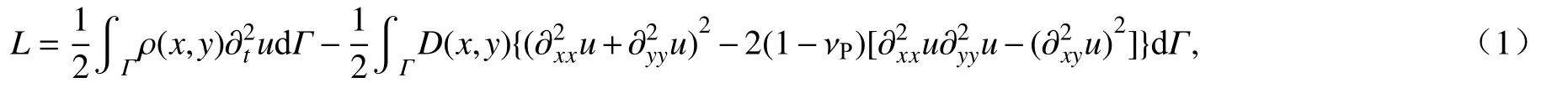
其中,Γ={(x,y)|x2+y2≤R2}为封装薄板平面区域，ρ(x,y)=ρ0h(x,y)为粘接有精密器件柔性薄板的面密度，u=u(t,x,y)为封装薄板面外振动位移，D(x,y)=Eh3(x,y)/(12(1−ν2P))为粘接有精密器件柔性薄板的面外抗弯刚度，ρ0,E和 νP分别为薄板（精密器件）材料的密度、弹性模量和Poisson 比，h(x,y)为粘接有精密器件柔性薄板(x,y)处的薄板厚度，即

式中，hi为第i个精密器件厚度（高度），hp为薄板厚度.

由Hamilton 变分原理，得到粘接精密器件柔性封装薄板振动控制方程为

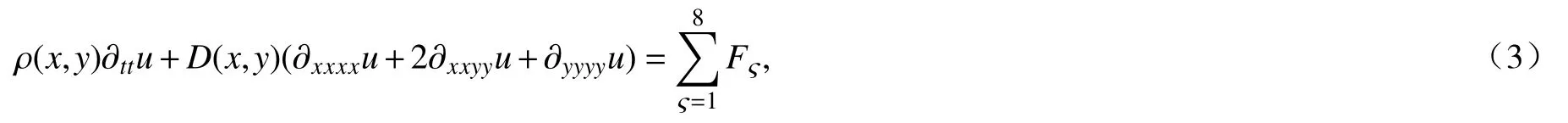
其中，R为封装薄板半径，ε为螺栓至封装薄板边界的最小距离.

初始条件和边界条件分别为

2 简化模型的动力学对称破缺与保结构分析

引入如下正则动量：∂tu=φ,∂xu=w,∂xw=ψ,∂x(ψ+κ)=q,∂yu=v,∂yv=κ,∂y(ψ+κ)=p，并定义状态向量z=(u,φ,w,ψ,q,v,κ,p)T，式(3)即可转化为以下一阶矩阵形式：

其中，S(z)=−ρ(x,y)φ2/2−D(x,y)(wq−ψκ+pv)+D(x,y)(ψ2+κ2)/2+为广义Hamilton 函数，系数矩阵为

值得注意的是，一阶矩阵形式(7)中，广义Hamilton 函数和系数矩阵均显含位置坐标，同时，广义Hamilton 函数含有非光滑的冲激函数.以上两个特点即是系统(7)的对称破缺因素.也正是因为上述对称破缺因素的存在，系统(7)只能称之为广义多辛形式而不能称之为严格的多辛形式[11-12].

由上述对称破缺因素决定的系统局部能量耗散可以表述为[11-12]

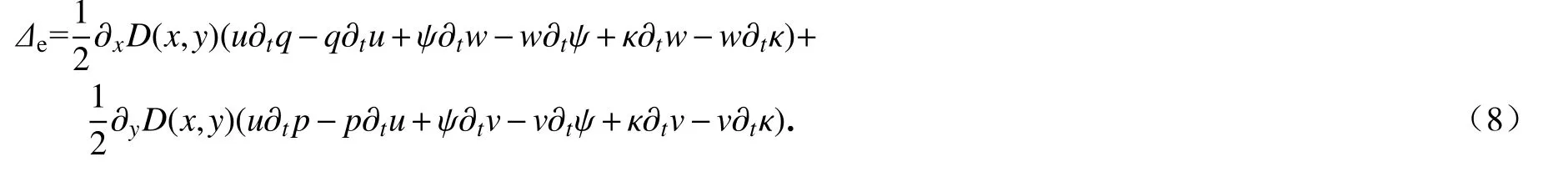
系统的局部能量耗散决定着系统局部动力学行为，因此，在后续数值算法构造及实现过程中，需要关注系统能量在非光滑边界处（冲激函数涉及的切换时间和边界位置）的能量耗散.

在薄板圆域内对求解区域 Γ={(x,y)|x2+y2≤R2}进行均匀剖分，剖分时设定空间步长分别为Δx和 Δy，并设定时间步长为Δt，采用隐式有限差分法对一阶矩阵形式(7)进行离散，得到一阶矩阵形式(7)的Preissmann 差分格式[16-17].消去其中的中间变量，得到与Preissmann 差分格式等价的离散格式：

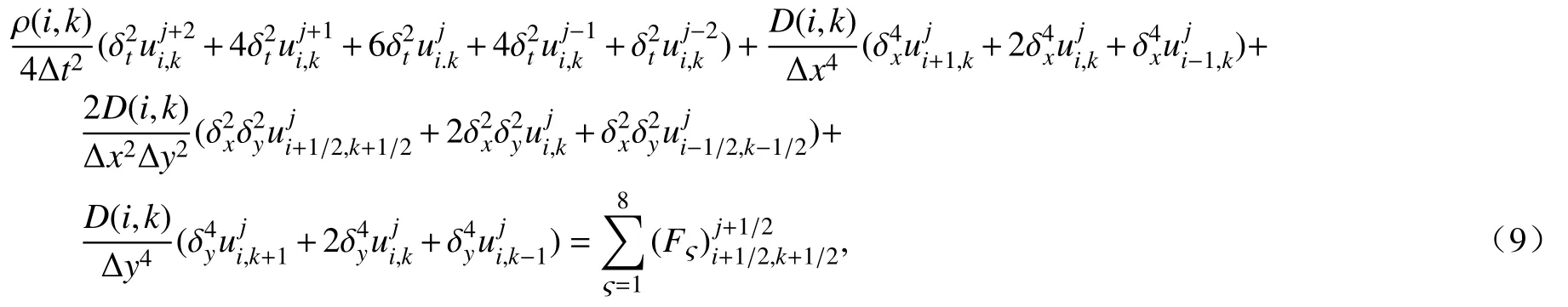
离散格式(9)中，

其中 Ξ={(j,i,k)|jΔt≤tς≤(j+1)Δt,iΔx≤xς≤(i+1)Δx,kΔy≤yς≤(k+1)Δy}.

相应的离散形式的局部能量耗散表述为

其中

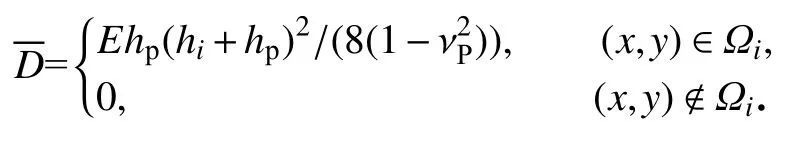
正是由于动力学分析算法(9)在每一步迭代过程中能够较为精确地保持系统的局部几何性质(局部能量耗散(11))，能够精确捕捉薄板上的局部共振区，才使得后续布局优化算法的优化效率得到大幅提高，这是本文布局优化设计相对于已有成果的最大特色和优势.

3 布局优化算法设计及优化算例

本节中，考虑了n个精密器件布置在半径为R的圆形柔性薄板上的情形.第i(i=1,2,···,n)个精密器件的特征尺寸以向量ai表示（本文仅考虑圆柱形状和直六面体形状的器件，圆柱形器件的特征尺寸向量包含底面半径和器件高度两个分量；直六面体器件的特征尺寸向量包含底面长度、底面宽度和器件高度三个分量）.在8 个连接螺栓处同时受到等大的冲击载荷作用下，以n个精密器件与封装薄板接触区域最大振动加速度的加权值作为优化目标，建立如下布局优化问题：

其中,wi为第i(i=1,2,···,n)个精密器件的权重（描述该电子器件对精度和稳定性的要求），(xi,yi)为第i(i=1,2,···,n)个精密器件底面与封装薄板接触面内的网格点坐标，dij为第i个精密器件边界与第j个精密器件边界间的最小距离，di为第i个精密器件边界与薄板边界之间的最小距离，δ1为满足散热要求和安装要求的最小器件间距，δ2为满足散热要求和安装要求的器件与封装薄板边界的最小间距.第i(i=1,2,···,n)个精密器件底面与封装薄板接触面内的网格点处的面外加速度值 ∂ttu(jΔt,xi,yi)由第2 节构造的保结构差分格式模拟得到.

上述布局优化问题的主要求解步骤如下：

1) 精密器件初始位置确定.采用保结构分析方法模拟未布置微电子器件柔性薄板面外振动，找到振动加速度较小的n个网格点作为n个微电子器件布置的初始中心位置共n!种情况，其中si为特征尺寸向量ai的维数，对于圆柱形器件，si=2；对于直六面体器件，si=3，取其中满足约束条件且wimax{∂ttu(jΔt,xi,yi)}最小的情况确定为微电子器件布置的初始中心位置组合.

2) 精密器件布局位置局部优化.以各精密器件底面几何中心坐标(xi0,yi0)为优化变量，为减小优化计算量，将各精密器件底面几何中心坐标(xi0,yi0)在 满足(约束条件的情况下，在δ3i（δ3i为第i个精密器件特征尺寸向量ai中除了器件高度外的较小的分量值）范围内摄动 这种优化方法虽然无法得到全局最优解，但是从后续优化过程中我们发现，这一过程能够有效降低wimax{∂ttu(jΔt,xi,yi)}的值，计算各种情形下wimax{∂ttu(jΔt,xi,yi)}的值，选取其中wimax{∂ttu(jΔt,xi,yi)}达到最小时的值，及对应的各精密器件底面几何中心坐标作为精密器件布局位置局部优化结果.

3) 精密器件布置方位优化.在确定了各精密器件底面几何中心坐标后，针对非中心对称底面的精密器件，以其精密器件底面几何中心坐标为局部坐标系原点，建立局部坐标系，以底面长边方位角 αi（以图2中x轴正向为起始方位）为优化变量，在满足约束条件的前提下，采用前述构造的保结构分析方法优化精密器件的布置方位，使得的值达到最小.

在数值算例中，系统的结构及材料参数假定为：hp=0.002 m,R=0.5 m,E=2.914×109Pa,νP=0.37，ρ0=1 kg·m−2,F¯ς=100 N.网格剖分步长及时间步长分别取为：Δx=Δy=0.002 m,Δt=0.001 s.

作为验证性算例，假定需要布局的精密器件有3 个，其基本参数如下：① 第一个器件为圆柱形器件，a1=[r,h1]T，其中r=h1=0.004 m；② 第二个器件为正四棱柱形器件，a2=[a2,h2]T，其中a2=h2=0.004 m；③ 第三个器件为直平行六面体器件，a3=[a3,b3,h3]T，其中a3=2b3=h3=0.004 m.

图3给出了精密器件布局优化过程中，精密器件加速度最大值的加权平均值a∗=随着迭代次数N的演化过程（在优化程序中，设定当a∗的迭代相对误差小于1 ×10−6时，优化迭代终止）.

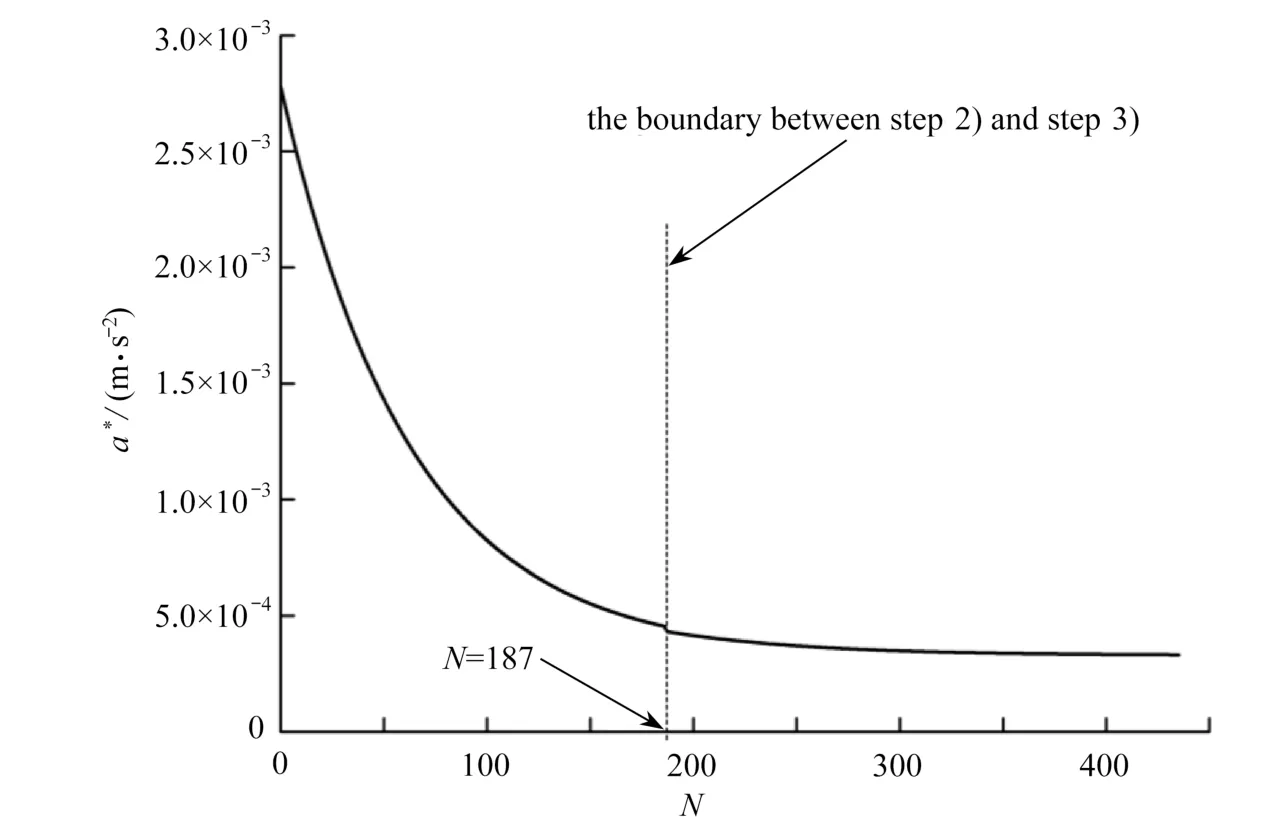
图3 精密器件加速度最大值加权平均值演化过程Fig.3 Evolution of the weighted average of the maximum accelerated speed of the precision device

从优化过程可以看出，精密器件布局位置局部优化过程的迭代步数为N=187，在这个过程中，精密器件加速度最大值的加权平均值从 0.002 78 m·s−2降低至 4.549 41×10−4m·s−2，降低约100%≈83.64%；精密器件布置方位优化过程的迭代步数为N=436−187=249，精密器件加速度最大值的加权平均值从4.549 41×10−4m·s−2降低至 3.322 92×10−4m·s−2，降低约×100%≈26.96%；整个优化过程中，精密器件加速度最大值的加权平均值降低约88.05%，优化效果较好.

4 结 论

确保航天器中精密电子元器件的工作稳定性是保障航天任务实施的重要内容.传统航天器结构设计过程中，先将精密电子元器件集中封装在若干块封装薄板上，然后将布置好电子元器件的封装薄板安装在航天器适当的位置.在这一过程中，航天器结构振动对精密电子元器件的影响有所考虑，但是，精密器件的布局对航天器局部振动特性的影响却被忽略了.实际上，精密器件的布局将改变航天器局部振动特性，甚至有可能在精密器件布置位置出现局部共振现象，因此，航天器设计过程中需要系统考虑精密器件布局优化问题.

本文考虑粘接有若干不同形状和尺寸大小的精密器件的柔性空间薄板振动问题，采用Hamilton 原理建立系统的振动方程；关注薄板振动的局部集合特性，基于广义多辛分析方法发展保结构算法模拟厚度非均匀薄板的振动特性；在采用保结构算法精确捕捉薄板局部共振区的基础上，以各精密器件布置位置薄板面外振动加速最大值的加权平均值作为优化目标，考虑各器件的形状和尺寸以及布置间隙要求等约束条件，对精密器件的布局进行优化设计.优化结果显示：基于保结构算法提出的精密器件布局优化设计方法能够有效降低航天器局部振动加速度，对航天器局部结构设计过程有一定的指导意义.