基于actor-critic算法的分数阶多自主体系统最优主-从一致性控制*

马丽新，刘 晨，刘 磊

（河海大学 理学院，南京211100）

引 言

多自主体系统的分布式协同控制广泛存在于自然界中，如鱼群、蜂群、鸟群等,近年来，在生物系统、传感器网络、无人机编队、机器人团队、水下机器人[1-4]等领域被大范围应用.一致性是多自主体系统分布式协同控制的基本问题之一，即多自主体在某种适当的协议下收敛到一个共同的状态.2002年，系统与控制领域的学者Fax 和Murray 首次运用控制理论的观点证明，通过对每个智能体设计仅仅依赖个体间局部信息交互的分布式控制协议，就能驱动整个多智能体系统完成状态一致的控制目标，并推导出一致性条件[5].后又有众多学者针对多自主体系统的一致性展开了研究[6-9].

由于分数阶微积分是整数阶微积分的推广，而且近年来越来越多的研究表明：众多实际系统运用分数阶模型才能反映出其更好的性质(黏弹性、记忆与遗传特性等）.所以，分数阶系统的相关研究引起国内外学者的广泛关注.随着分数阶系统逐渐被重视,节点带有分数阶动力学网络系统的一致性逐渐成为当下的热点问题之一,可参考文献[10-12].

随着网络技术的发展，考虑到通信带宽、资源利用率等问题，Astrom 等在文献[13]中提出事件触发控制技术以减少信息传递与调整控制器的次数.2009年，Dimarogonas 等[14]将事件触发机制引入到了多智能体系统.2014年，Xu 等[15]提出事件触发控制策略来研究分数阶多自主体系统的一致性问题.2017年，Wang 等[16]研究了基于指数型事件触发策略下的非线性分数阶多自主体系统的主-从一致性.此外，间歇控制策略因具有减少控制器持续运作时间的功能，对于解决实际工程上控制器设备限制等问题上有一定优势，近年来被越来越多的学者应用到分数阶多自主体系统的一致性控制问题上[17-19].为发挥这两种控制策略的优势，部分学者将两者有机整合，提出基于间歇策略的事件触发机制[20-22].

2005年，Ren 等[23]提出了一个开放性问题：如何设计一个分布式协议，在使得多智能体系统达到一致性的前提下，又能够优化某些性能指标.针对整数阶多自主体系统，Zhang 等[24]基于强化学习方法研究了离散时间多自主体系统的最优一致性控制问题.Zhao 等[25]利用自适应动态规划技术，提出了一种具有扰动的未知非线性多智能体系统的事件触发一致性跟踪控制策略.Dong 等[26]研究了带有控制约束的连续时间系统的事件触发自适应动态规划方法.刘晨等[27]研究了基于事件触发策略的多自主体系统的最优主-从一致性.

相对整数阶，分数阶微积分的分析工具不够完善，HJB 方程求解困难，其最优一致性尚未被充分研究.因此，本文的主要目的就是进一步填补空白，采用强化学习中的actor-critic 算法研究分数阶多自主体系统的最优主-从一致性，设计基于周期间歇事件触发策略的强化学习算法结构.

1 预备知识

分数阶微分有多种定义方式，常用的是Riemann-Liouville 型(简称R-L 型)分数阶微分、Caputo 型分数阶微分以及Grünwald-Letnikov 型分数阶微分等.R-L 型分数阶微分在数学上有很好的性质，但相比而言,Caputo 型分数阶微分的初值物理意义明确，很早就得到了广泛的应用[28].本文中分数阶多自主体系统的动力模型均由Caputo 型分数阶微分描述.下面介绍Caputo 型分数阶微分的定义、一阶逼近以及基本性质.

定义1[28]Caputo 型分数阶微分算子定义：

其中 α >0,n=[α]+1.

根据文献[29-31]，当0 <α<1,函数x(t)∈C2[t0,tf]时，可得到Caputo 型微分算子的一阶展开式逼近：

其中

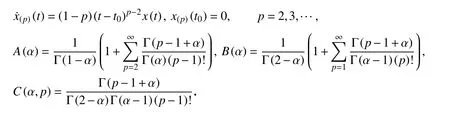
定义2[28]f(t),g(t)∈C1[a,b],α>0,β>0,则

2 问题描述

2.1 模型描述

考虑带有领导者的分数阶多自主体系统：

其中阶数 0 <α<1,x0(t)=(x01(t),x02(t),···,x0n(t))T∈Rn表示领导者的状态，xi(t)=(xi1(t),xi2(t),···,xin(t))T∈Rn表示第i个自主体的状态，ui(t) 表示第i个自主体的控制输入，f:R×Rn→Rn是连续可微的向量函数.

定义3若对任意的初始状态xi(t0)，可找到ui(t)使得 l imt→∞‖xi(t)−x0(t)‖=0，则称该分数阶多自主体系统(2)可达到主-从一致，对∀i=1,2,3,···,N.

定义第i个追随者与领导者之间的状态误差如下：

将领导者和各追随者均看作节点，得到节点集v={0,1,2,···,N}.对称矩阵A=(aij)N×N,aij≥0表示各追随者间的通讯情况，aij>0表示i节点与j节点有通讯，反之，i,j节 点间无信息流通.进而用Ni={j∈v|aij≠0}来表示节点i的相邻节点集合.对角矩阵B=(bi)N×N表示领导者(0 节点)与各追随者间的通讯情况，bi>0代表0节点与i节点有交流，反之没有.

则全局状态误差可表示为

其中 ⊗为Kronecker 乘积符)号，x(t)=(xT1,xT2,···,xTN)T∈RnN表示全局状态向量，x～0(t)=(xT0,xT0,···,xT0)T∈RnN.定义度矩阵则Laplace 矩阵L=D−A.

注1因为H为正定阵，所以δ(t)→0 等价于x(t)→(t)，即xi(t)→x0(t),i=1,2,···,N，代表系统达到主-从一致.

针对分数阶多自主体系统(2)，本文不仅考虑如何让系统达到主-从一致，还考虑在系统达到主-从一致的过程中的能量消耗，因此引入性能指标的概念.

定义第i个自主体的性能指标为

其中P(δi)=δTi(t)Qiδi(t)是过程代价，与一致性性能相关，度量了系统在达到一致性过程中的一致偏差，代表的是“运动能量”；W(ui,uj)=uTi(t)Riui(t)+是控制代价，代表的是“控制能量”，Qi≥0,Ri>0,Rj>0.

本文的目的是对于每个自主体i，找到合适的控制器ui(t),uj(t)，使得系统(2)在达到主-从一致的同时性能指标最小：

由式(6)得自主体i的Lyapunov 方程为

另外，由Caputo 型微分算子一阶逼近式(1)和系统动力模型(2)得

其中

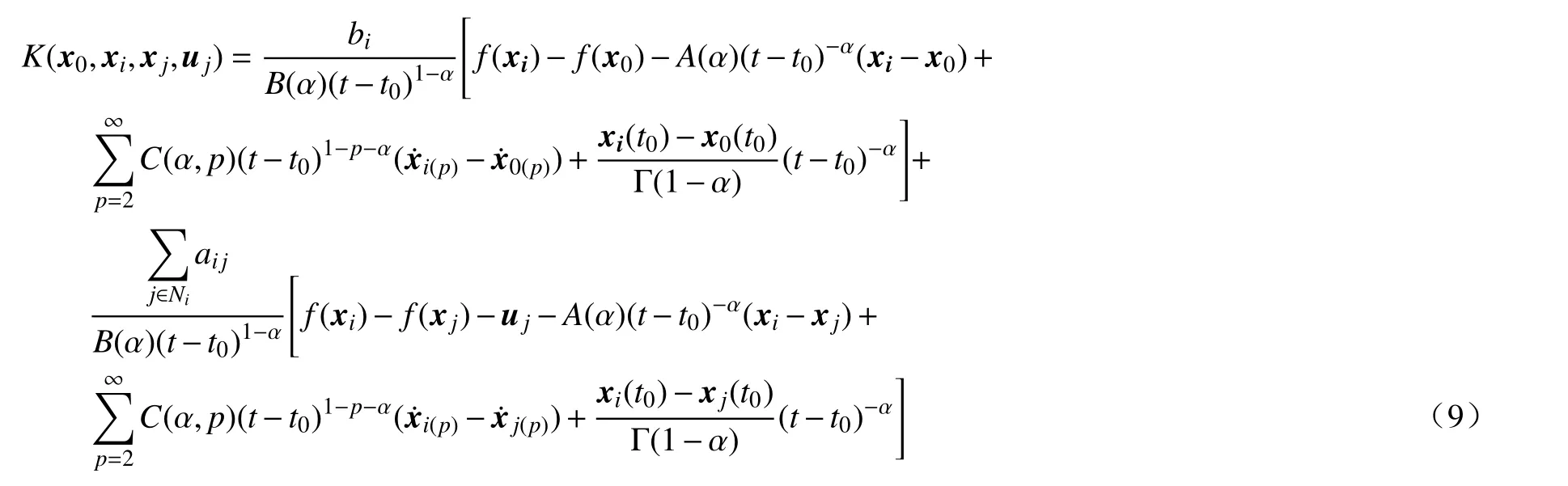
与ui无关.

则方程(7)等价于

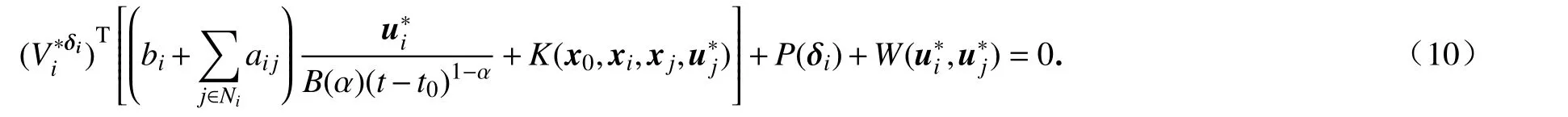
根据Bellman 最优性原理可得第i个自主体的最优控制为

2.2 周期间歇事件触发策略

对于分数阶多自主体系统(2)，设计周期间歇反馈控制器：

其中0 ≤ρ ≤1为休息率，相对地，1−ρ为工作率，T为控制周期，k=0,1,2,3,···.

在周期间歇的基础上考虑集中式事件触发策略.设第k个周期内的触发时刻集合为{tk1,t2k,t3k,···,tkm,···}，则整个过程的事件触发时刻序列可表示为{t10,t20,t30,···,tm0,···,t1k,tk2,t3k,···,tmk,···}.若在第k个周期 [kT,(k+1)T)上已知tmk，则下一触发时刻tmk+1由下式给出：

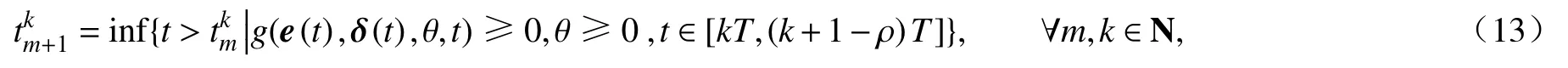
其中e(t)=(eT1(t),eT2(t),···,eTN(t))T为全局状态测量误差,ei(t)=δi(tkm)−δi(t)表示第i个自主体状态测量误差.

考虑到周期间歇事件触发策略，自主体i的误差动力学可写为如下分段形式：

其中ui(tmk)表示(tmk,tmk+1)区间内i自主体的控制输入.

注2式(13)中事件触发条件g(e(t),δ(t),θ,t)可根据具体一致性种类和控制策略来设计.针对分数阶多自主体系统的事件触发条件大致可分为三类：依赖于状态[26]、依赖于指数函数[16]、依赖于状态和指数函数的混合[20].

注3周期间歇事件触发策略仅在工作区间[kT,(k+1−ρ)T],k∈N 内采用事件触发策略，在其他时间段不对系统施加控制.当ρ=0 时，此策略退化为事件触发控制策略；当ρ=1时，此策略退化为事件触发脉冲控制策略.

3 基于actor-critic 算法的近似最优控制

Actor-critic 算法是强化学习中的一种算法，简要原理是actor 来做动作，critic 对actor 做出的动作给予评价.评价分为奖励、惩罚两种.actor 通过得到的评价不断调整自己的动作以得到更多的奖励.下面用critic 网络拟合性能指标函数，actor 网络拟合控制器ui(t).算法整体框架详见文后附录.

3.1 Critic 网络设计

根据式(5)，确定critic 网络的输入Zci(t)必须包含的信息由actor 网络生成）.对于第i个自主体，网络拟合的性能指标为

其中Yci(t)表示输入层到隐含层的权重，Wci(t)表示隐含层到输出层的权重，ψc(·)为激活函数.

由式(7)可得

进而

因为网络拟合存在重构误差，所以定义critic 网络的误差函数：

Critic 网络训练的目的为：选择合适的Yci(t),Wci(t) 使得Eci(t)=尽量小.

当达到周期间歇事件触发阈值时，使用梯度下降法对网络权重进行更新，否则权重不更新，具体更新方式如下：

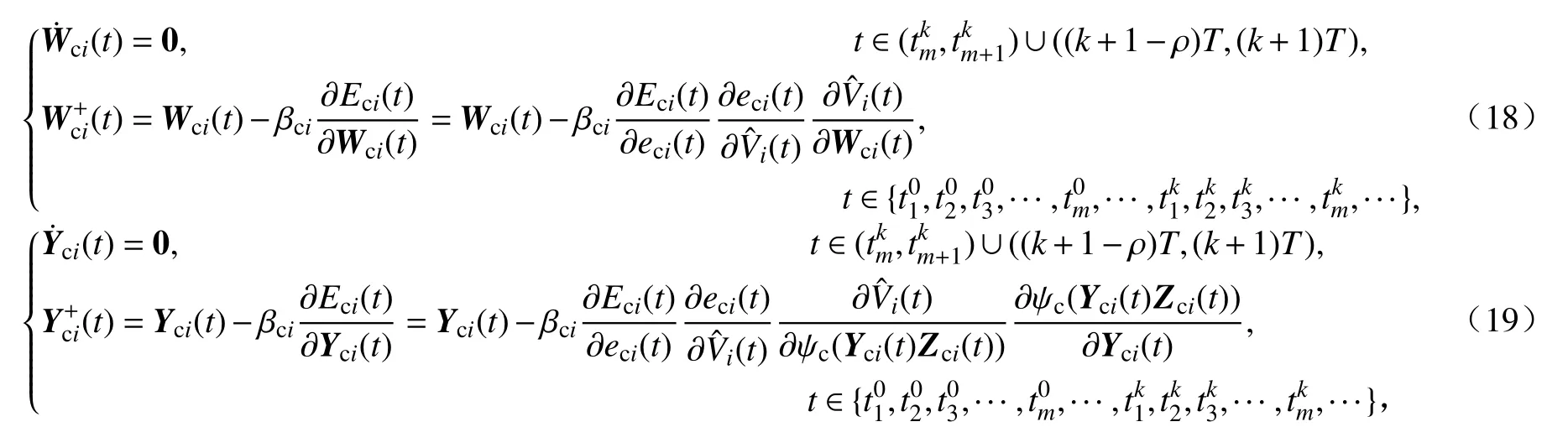
其中 βci为学习率.

3.2 Actor 网络设计

与critic 网络类似，actor 网络同样采用三层的网络结构.对于第i个自主体，以 δi(t)作为actor 网络的输入，得到网络拟合的控制器为

其中Yai(t)表示输入层到隐含层的权重，Wai(t)表示隐含层到输出层的权重，ψa(·)为激活函数.

无论是critic 网络还是actor 网络，最终目标是找到合适的控制器(t)使得系统达到主-从一致时性能指标最 小（理想目标是Uc=0），所以定义actor 网络的误差函数为

Actor 网络训练的目的为：选择合适的Yai(t),Wai(t)使得Eai(t)=(t)尽量小.

Actor 网络的权值更新方法与critic 网络类似，具体公式如下：

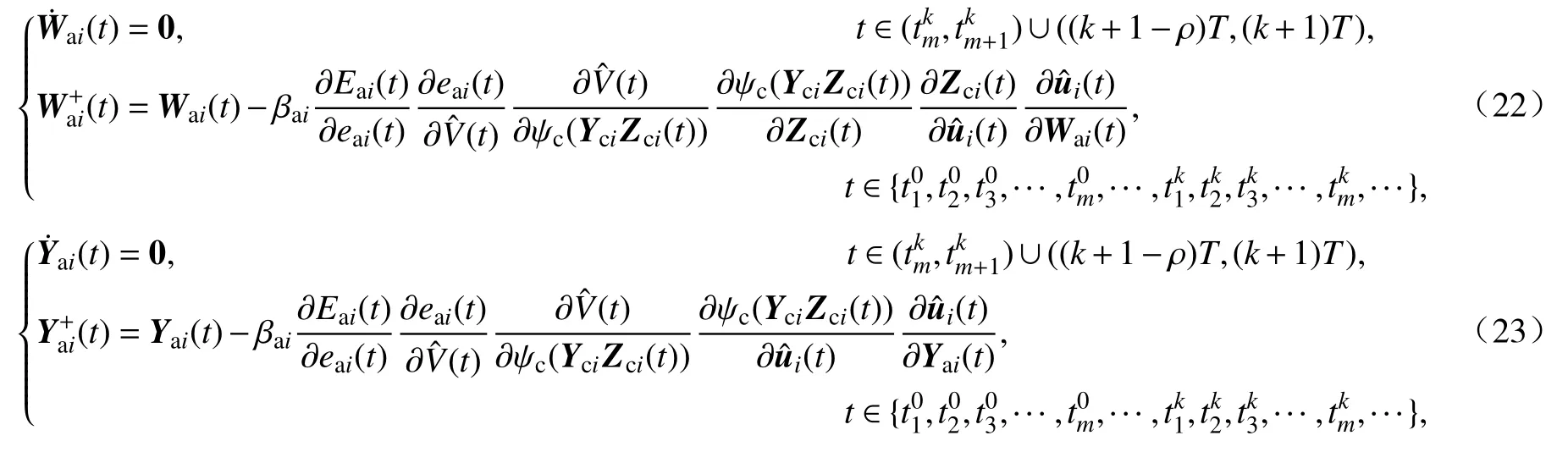
其中 βai为学习率.

注4本文将分数阶微分的一阶导近似展开式(1)和文献[27]中整数阶多自主体系统的事件触发自适应动态规划算法有机整合，进一步考虑了间歇策略，针对分数阶多自主体系统的最优主-从一致性，设计了基于周期间歇事件触发的强化学习算法.

4 数值仿真

例1考虑带有1 个领导者，3 个追随者的分数阶多自主体系统，网络拓扑图如图1.

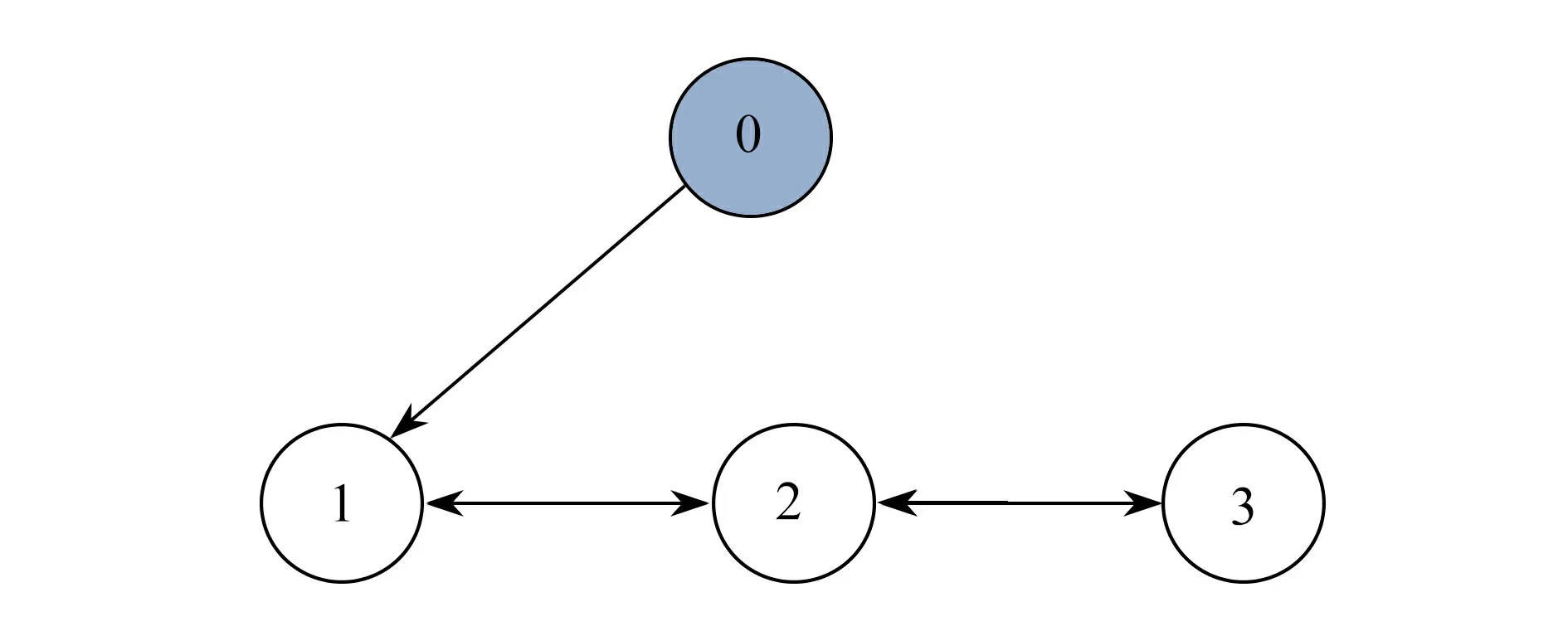
图1 多自主体系统网络拓扑图(1 个领导者，3 个追随者)Fig.1 The net topology of the multi-agent system (1 leader,3 followers)

选取 α=0.95,A=[0 1 0;1 0 1;0 1 0],B=[1 0 0;0 0 0;0 0 0]f(xi)=−2sin(xi)+tanh(xi),i=0,1,2,3，初始状态x0(0)=5,x1(0)=−3,x2(0)=−1,x3(0)=2.8，时间步长h=0.001 s.若无任何控制器作用，各自主体的轨迹如图2.

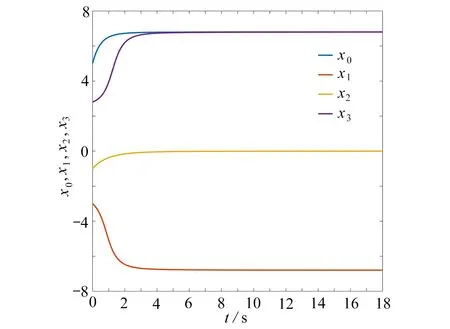
图2 无控制器作用时，各自主体的状态轨迹(1 个领导者，3 个追随者)Fig.2 State trajectories of each agent without controllers (1 leader,3 followers)

设置基于周期间歇的事件触发策略：T=3.5 s,ρ≈0.143,g(t)=e(t)−θδ(t)，取 θ=0.06，权值矩阵的初值在区间[-0.025,0.025]中随机选取，并归一化处理，其他网络参数设置如表1.

表1 网络参数设置Table 1 Values of networks’ parameters

在该策略控制作用下的数值仿真结果如图3～5 所示.图3为各自主体的状态轨迹图，表示系统约在10 s 达到主-从一致的状态.图4为全局状态测量误差 ||e(t)||及事件触发阈值的变化曲线，可看出在接近9 s的时候||e(t)||便趋于0.图5为基于周期间歇的事件触发时刻图，描述了在0～18 s 中事件触发时刻的具体分布：0～3 s，3.5～6.5 s，7～10 s，10.5～13.5 s，14～17 s，17.5～18 s为控制器工作时间;3～3.5 s，6.5～7 s，10～10.5 s，13.5～14 s，17～17.5 s为控制器休息时间.

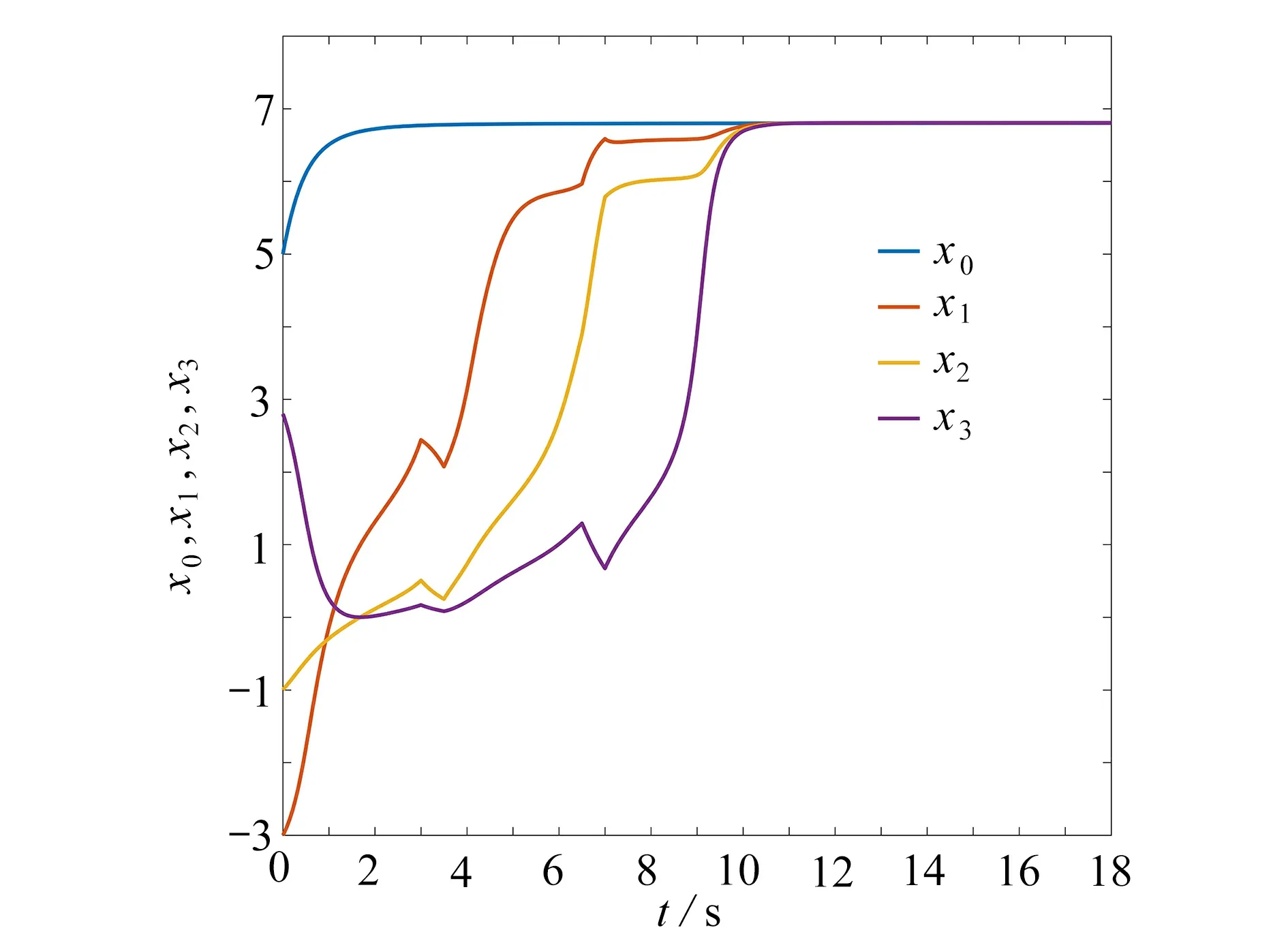
图3 各自主体的状态轨迹(1 个领导者，3 个追随者)Fig.3 State trajectories of each agent (1 leader,3 followers)

图4 ‖e(t)‖及触发阈值变化曲线(1 个领导者，3 个追随者)Fig.4 The error and the trigger threshold (1 leader,3 followers)

图5 周期间歇事件触发时刻分布Fig.5 The event-trigger moment distribution of periodic intermittence

注5本文将间歇的事件触发机制有机整合起来，研究了分数阶多自主体系统的最优主-从一致性.目前该方向仅有少量成果.文献[20]采用了间歇事件触发策略，对分数阶多自主体系统进行了有界性分析，对于一致性的研究尚未有文献涉及.

例2考虑带有1 个领导者，4 个追随者的分数阶多自主体系统，拓扑结构如图6.

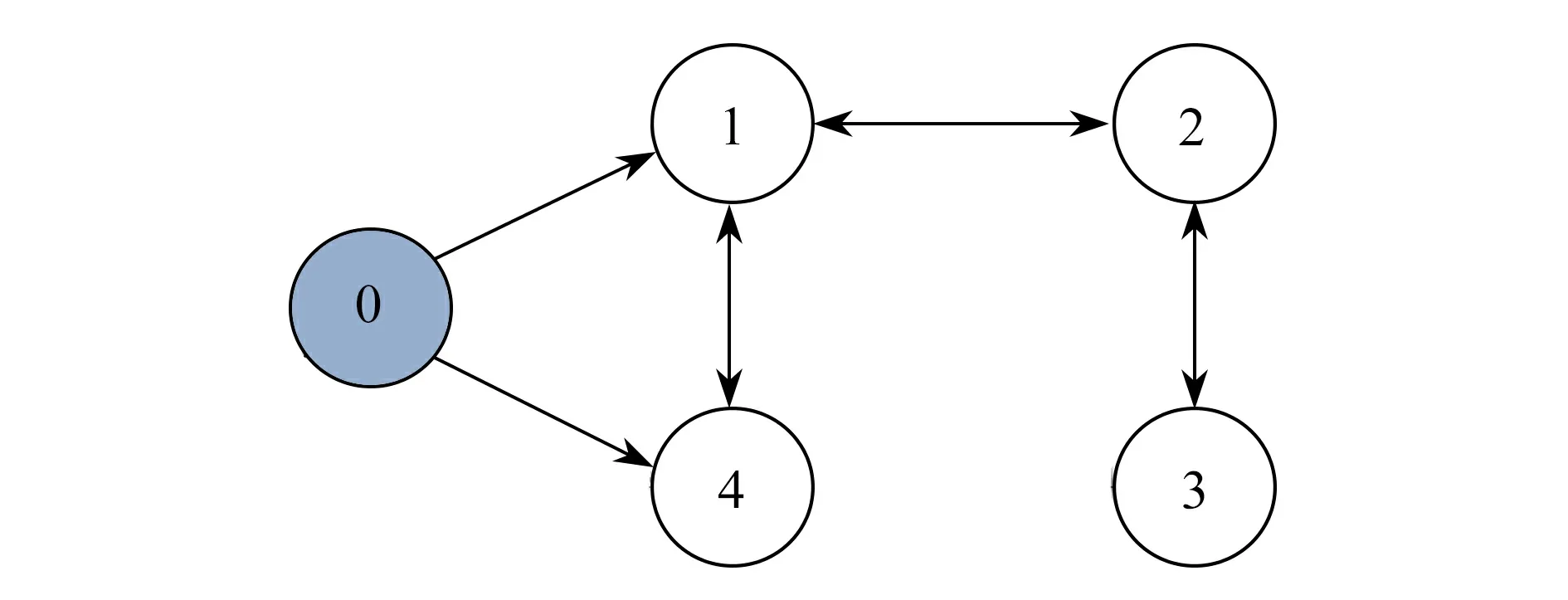
图6 多自主体系统网络拓扑图(1 个领导者，4 个追随者)Fig.6 The net topology of the multi-agent system (1 leader,4 followers)

选取α=0.86,A=[0 1 0 1;1 0 1 0;0 1 0 0;1 0 0 0],B=[1 0 0 0;0 0 0 0;0 0 0 0;0 0 0 1]，f(xi)=tanh(0.01xi)−2cos(xi),i=0,1,2,3,4，初始状态x0(0)=5,x1(0)=4,x2(0)=3,x3(0)=2,x4(0)=6,时间步长h=0.001 s.若无任何控制器作用，各自主体的轨迹如图7所示.

图7 无控制器作用时，各自主体的状态轨迹(1 个领导者，4 个追随者)Fig.7 State trajectories of each agent without controllers (1 leader,4 followers)

设置基于周期间歇的事件触发策略：ρ=0，g(t)=‖e(t)‖−e−0.5θt，即事件触发策略.选取参数θ=1.9，其他网络参数如同例1.数值仿真结果如图8～10 所示.图8为本文所设计控制器作用下各自主体的状态轨迹图.由图8看出，系统在不到3 s的时间内就达到了主-从一致.图9为全局状态测量误差‖e(t)‖及事件触发阈值的变化曲线，其表明系统误差在慢慢变小，并在3 s 后非常接近于0.图10为事件触发时刻图，描述了0～12 s 内事件触发的具体时刻分布，触发40 次.

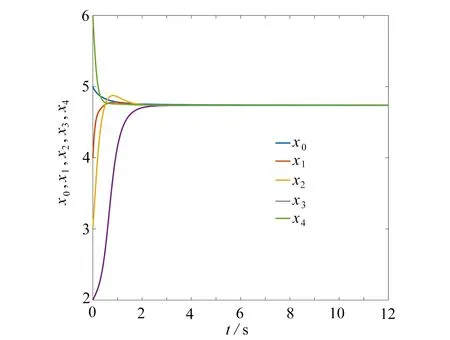
图8 各自主体的状态轨迹(1 个领导者，4 个追随者)Fig.8 State trajectories of each agent (1 leader,4 followers)

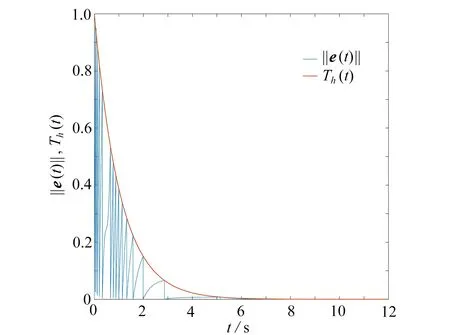
图9 ||e(t)||及触发阈值变化曲线(1 个领导者，4 个追随者)Fig.9 The error and the trigger threshold (1 leader,4 followers)

图10 事件触发时刻分布Fig.10 The event-trigger moment distribution

注6图11展示了文献[16]中控制器作用下各自主体的状态轨迹.对比图8和图11，网络拟合控制器将系统趋于一致的速度提高了不止1 s.图12为文献[16]控制器下系统达到主-从一致过程中的全局状态测量误差变化情况.图13为事件触发时刻图，描述了0～12 s 内事件触发的具体时刻分布，触发104 次.通过图10和图13可明显看出，在系统达到主-从一致的过程中本文所设计控制器作用下的事件触发次数较少，一定程度上减少了通讯成本.

图11 文献[16]控制器下，各自主体的状态轨迹图Fig.11 State trajectories of each agent under ref.[16]

图12 ||e(t)||及触发阈值变化曲线Fig.12 The error ||e(t)|| and the trigger threshold

图13 事件触发时刻分布Fig.13 The event-trigger moment distribution

5 总 结

本文借助分数阶微分的一阶近似逼近和强化学习中的actor-critic 算法，研究了在控制器周期间歇时，分数阶多自主体系统在事件触发策略下的最优主-从一致性问题，最终设计出基于actor-critic 算法的控制策略，并通过仿真验证了其有效性.

附 录

Actor-critic 近似最优控制算法整体框架如下：

输入：actor 模型πWai,Yai(δi)，critic 模型VWci,Yci(xi,ui,uj)，i=1,2,···,N.

1 Fori=1,2,···,N

2 初始化状态xi，得到初始 δi，初始化参数Wai,Yai,Wci,Yci

3 End for

4 Fort∈[kT,(k+1)T)

5 Ift∈[kT,(k+1−ρ)T]，即控制器处于工作时间

6 Fori=1,2,···,N

7 遵循策略πWai,Yai(δi)，得到控制ui

8 在ui的作用下，自主体i得到新状态x′i以 及回报ri=Vi

9 End for

10 计算全局状态误差δ(t)=(δT1(t),δT2(t),···,δTN(t))T

11 全局状态测量误差e(t)=(eT1(t),eT2(t),···,eTN(t))T

12 If 系统达到事件触发条件的阈值：g(e(t),δ(t),θ,β,t)≥0

13 Fori=1,2,···,N

14 If 自主体i的神经网络满足网络误差阈值

15 更新网络权重，得到新的策略πW′ai,Yai(δi)

16Wai←Wai+βai∇aiπWai,Yai(δi)

17Yai←Yai+βai∇aiπWai,Yai(δi)

18Wci←Wci+βci∇ciVWci,Yci(xi,ui,uj)

19Yci←Yci+βci∇ciVWci,Yci(xi,ui,uj)

20 End if

21 End for

22 End if

23 Else，即控制器处于休息时间

24 Fori=1,2,···,N

25 根据ui=0时的状态方程计算得出自主体i的新状态x′i

26 End for

27 End if

28 End for