基于自适应分段云模型的单相用户相别辨识方法

刘 苏，黄 纯，李克明，侯帅帅

（湖南大学电气与信息工程学院，湖南省长沙市 410082）

0 引言

低压配电网中多为单相用户，台区中精准的用户相别关系是进行线损分析、故障诊断、三相平衡等应用功能的基础，对提高供电可靠性和供电服务能力至关重要。但是，台区中用户与台区配电变压器（简称台变）的相别关系变化相对频繁，漏报、误报的情况普遍存在，严重影响了配电网的精细化管理［1-5］。目前，电网公司主要采用人工排查和拓扑识别仪2 种方式进行相别辨识：人工方法主要依靠工作人员现场排查用户的所属台区，并且手动记录，存在人力成本高、效率低的问题［6］；拓扑识别仪需要额外增加设备投资，经济成本高［7］。为提高低压配电台区的管理水平，亟须研究一种用户与台变相别关系的自动判断方法。

近年来，随着智能电表等终端设备在配电网的普及，电网对台变和用户电气量的采集尤为方便，为相别辨识奠定了信息基础。目前，低压配电台区用户相别辨识方法主要有以下几种：

1）传统的相关性分析方法，如皮尔逊相关系数（Pearson correlation coefficient，PCC）［8］、灰 色 关 联分 析（grey relational analysis，GRA）［9］、弗 雷 歇 距离［10-11］、动 态 时 间 弯 曲（dynamic time warping，DTW）算法［12］等，当电压数据接近时这类方法区分度不明显。

2）线性规划方法，如二次规划［13-14］、混合整数线性规划（mixed-integer linear programming，MILP）［15］等，但模型相对复杂，对用电量为0 或极小的用户不敏感。

3）多元线性回归及降维方法，如线性回归（linear regression，LR）分析法［16］、主成分分析法［17］、t分布的随机近邻嵌入（t-distributed stochastic neighbor embedding，t-SNE）［18］等。文献［16］构建了以单相电表电压为因变量，以关口电表电压、电流和单相电表电流为自变量的多元线性回归方程。文献［17］利用主成分分析法对变压器和用户的电压数据进行数据预处理，以达到降维的目的。文献［18］利用t-SNE 降维算法对电压数据进行特征提取，但采用的数据驱动原理相对复杂。

4）聚类方法，如K-means［19］、K-medoids［20-21］、谱聚类［22］、约束多树聚类［23］、基于层次结构的平衡迭代聚类（balanced iterative reducing and clustering using hierarchies，BIRCH）［24］等。这 类 方 法 存 在 聚类数和初始聚类中心选取困难的问题，且对噪声和离群点敏感，聚类中心会受到异常数据的干扰。

本文提出自适应分段云模型的相似度（similarity of adaptive piecewise cloud model，SAPCM）算法评估台变相电压与用户电压的相似性，从而进行相别辨识。与已有研究相比，SAPCM算法利用云模型的数字特征将台变相电压与用户电压的波动趋势这一定性概念转化为定量概念，采用云模型的形状差异反映出不同相中电压波动的趋近性。通过定义指标自适应地对电压序列云模型进行分段，得到的电压相似性结果不受台区拓扑结构和用户负荷变化等的影响，具有通用性。该方法解决了台变三相电压接近时，传统相似性方法相别辨识时误判率高的问题，基本不受分布式电源（distributed generator，DG）及随机误差的影响，相别辨识准确率高。

1 单相用户相别辨识基本原理

1.1 电压波动的相似性

低压配电网接入用户众多且多为单相用户，用户负荷的波动使台变三相电压与各用户电压也处于波动状态。处于同一相的用户由于电气距离相对较近，台变相电压及用户电压波动曲线相似性较高。处在不同相的用户，由于其电气距离相对较远，电压波动曲线相似性较低。

1.2 云模型

云模型是研究定量数据和定性概念之间不确定性转换的理论，云的整体形状反映了用定量数值表示的定性概念：台区内同一相中电压波动的趋近性。基于电压波动特征，本文采用云模型解决相别辨识问题符合云模型的理念：

1）台区中负荷变化的随机性，使得台区中电压变化亦呈现随机性；

2）处于台变同一相的用户电压随着负荷的变化呈现相近的变化趋势，这个变化趋势不可求，是模糊的，但确是真实存在的。

不同电压序列的波动特征通过云模型的整体形状特征定量表示，即云模型的形状差异反映电压序列波动的差异。通过比较不同形状云模型的相似性，得到不同电压序列电压波动的趋近性。2 个云模型的相似性越大，说明这2 个电压序列的电压波动情况越接近，越有可能属于同一相。

设某一电压序列X=[x1，x2，…，xn]，其中n为电压序列中元素的数目。采用由3 个参数即期望Ex、熵En和超熵He组成的向量来表示云的数字特征的模型，称为电压序列X的云模型CX=[Ex，En，He]，云模型的数字特征计算详见附录A。

1.3 自适应分段

在整个采样时间内求取电压序列的云模型，仅仅得到电压波形的全局特征。在实际应用中，台变的三相电压波形非常接近，仅通过全局特征无法准确进行用户相别辨识，需要对采集的电压波形分段，来分析电压波形的局部特征。

本文提出的SAPCM 算法具有以下2 个优点：一是可以自适应地确定电压序列分段总数；二是可以自适应地确定每一个时间段的起始时刻，使得各分段内部数据特征趋于近似，各分段之间数据特征趋于不同。

1.3.1 自适应确定分段总数

本文提出电压序列云模型自适应分段的有效性评价指标τ，包括以下2 个方面：

1）基于云模型期望的段间区分度α。云模型的数字特征期望反映了云滴群的云重心。无论2 个云模型的形状如何，2 个云模型的期望值越接近，这2 个云模型的相交面积就越大，2 个云模型就越相似。该评价指标在云模型自适应分段过程中，保证段与段之间的Ex差距大，使得段间差异大。

2）基于云模型熵的段内趋近度β。在云模型中，熵被用来综合评估定性概念的模糊度和概率，熵值越大，定性概念所接受的数值范围就越大，概念越模糊，数值也越不稳定。反映到相别辨识中，即熵值越小，电压波动的特性越能得以清晰表现。通过不断对分段云模型中熵值最大的时间段进行分段，尽可能使每一段电压序列波动特征更为明显［25］。

对于任意一条电压序列X=[x1，x2，…，xn]，假设将其分成λ段子序列，即Y=[Y1，Y2，…，Yλ]，将每一段子序列Yi用云模型表示，即CY，i=[Ex，i，En，i，He，i]，其 中Ex，i、En，i、He，i分 别为第i段 电压序列云模型的期望值、熵值、超熵值。则分段后的电压序列云模型的段内趋近度β(λ)计算如下：

式中：λ为电压序列分段总数，λ∈[2，n]。

分段后的电压序列云模型的段间区分度α(λ)计算如下：

基于式（1）和式（2），得到电压序列云模型分段的有效性评价指标τ，计算如下：

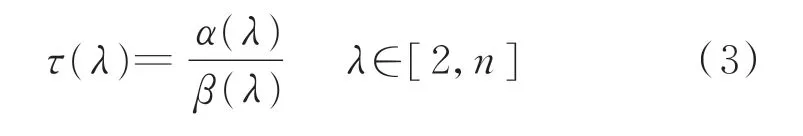
α(λ)值越大，说明某一电压序列分成的各段相似性越低。β(λ)值越小，说明分成的各段内部差异性越小，电压序列波动特征越明显。因此，τ(λ)值越大，说明自适应分成的段数效果越好，即电压序列段内相似性大、段间相似性小。τ(λ)的最大值对应的λ值λbest即为电压序列自适应分段的总数。

1.3.2 自适应确定每段的起始时刻

先根据1.3.1 节确定电压序列自适应分段的总数，再确定每段的起始时刻，具体步骤［26］见附录A表A3。

电压序列云模型的数字特征熵En表示论域中云滴的离散程度，其值越小，在该时间段内电压波动特征就越明显。因此，电压序列自适应分段的过程就是不断对分段云模型中En值最大的时间段进行分段，直至满足分段总数。

综上所述，自适应分段云模型算法可以自适应地确定任意一条电压序列的分段总数以及自适应地确定每一分段的起始时刻，可以从全局和局部角度充分分析电压序列的形态特征，并实现特征表示。

1.4 自适应分段云模型相似度计算方法

根据1.3 节中自适应分段算法将任意电压序列按照一定规则分成若干时间段，通过计算2 个电压序列若干时间段的云模型相似度得到这2 个电压序列的相似度。

为确定2 个电压序列各分段中参与相似度计算的分段，定义云模型匹配对如下：若电压序列A中分段am与B中分段bn时间上有交集，则说明am与bn构成云模型匹配对。

通过云模型的相似度计算方法求取云模型匹配对的相似度，如云模型的余弦相似度法（linkness comparing method based cloud model，LICM），云模型的形状相似度（shape based cloud model，PCM），基于期望曲线的云模型相似度（expectation based cloud model，ECM），基于最大边界曲线的云模型相似度（maximum boundary based cloud model，MCM）和基于期望曲线重叠度的云模型相似度（overlap based expectation curve of cloud model，OECM）等，具体算法介绍见附录B。

电压序列A和B自适应分段云模型的相似度计算公式见附录A 式（A3）至式（A7）。

2 相别辨识的算法流程

基于SAPCM 算法对低压台区内单相用户相别辨识的具体步骤如下：

步骤1：首先从配电变压器终端获得台变低压侧三相电压时间序列数据，从用户智能电表获得相同时间段内台区各用户的电压序列；

步骤2：按照Z-score 标准化原理对台变相电压和用户电压进行标准化处理；

步骤3：根据SAPCM 算法确定获得的台变相电压和用户电压序列自适应分段的总数以及每一分段的起始时刻和结束时刻；

步骤4：根据SAPCM 算法计算步骤3 中已经分段的电压序列的相似性；

步骤5：确定待检测用户的相位连接关系，完成用户相别辨识。

3 相别辨识算例分析

3.1 低压配电台区拓扑结构

采用某地区供电所中一典型台区一天的电压数据作为案例，采样周期为15 min。为方便叙述，选用台区中已经确定相别的13 个用户的电压数据。低压配电台区拓扑结构如图1 所示，用户C1至C5挂接在台变A 相，用户C6至C9挂接在台变B 相，用户C10至C13挂接在台变C 相。图中，UA、UB、UC分别为A相、B 相、C 相的电压。

图1 低压配电台区拓扑结构Fig.1 Topology of low-voltage distribution station area

3.2 电压序列自适应分段

3.2.1 确定每一电压序列分段总数

根据某供电所“台区电压透抄统计表”提供的该典型台区台变A、B、C 三相和13 个用户一天的电压数据，按照1.3.1 节中的原理确定这16 个电压序列自适应分段的总数。

假设电压序列自适应分成的总段数为λ，λ∈[2，11]，探究16 个电压序列自适应分段有效性指标τ随λ的变化。以A、B、C 三相电压序列和用户C1、C6、C10电压序列的τ随λ变化曲线为例，如附录C图C1 所示。由图C1 可得，当分段总数为3 时，台变A、B、C 三相电压序列与用户C1、C6、C10电压序列自适应分段的有效性指标τ达到最大，此时段内相似性相对较高，段间相似性相对较低，电压序列的分段效果最好。其他用户也均是在分段总数为3 时分段效果最好，具体数据见附录C 表C1。

3.2.2 自适应确定电压序列每一分段起始时刻

由3.2.1 节分析可知，16 个电压序列均自适应分成3 段。以台变A、B、C 三相电压序列为例，根据1.3.2 节中自适应分段云模型算法求取电压序列每一分段的起始时刻，如附录C 图C2 所示。

A、B、C 三相以及13 个用户电压序列云模型的自适应分段结果见附录D。

3.3 电压序列云模型相似性计算结果

为验证LICM、PCM、ECM、MCM 和OECM 这5 种云模型相似性量度方法对相别辨识的可行性，首先将本算例中台变三相以及13 个用户归一化的电压序列分别用以上5 种方法计算，得到每个用户与A、B、C 三相的相似度，结果见附录E。从附录E中可以看出，5 种方法计算的结果均超过0.9，并且数值没有区分度，无法对用户所属台变相位关系进行辨识。由于台变三相电压接近，仅仅分析电压序列云模型的整体特征无法区分出用户电压与三相电压的接近程度，需要按照一定规则对电压序列进行分段，剖析电压序列的局部特征。

因此，本文利用SAPCM 算法，通过对电压时间序列整体的有效划分，计算2 个电压序列相匹配的时间段云模型的相似性，再进行整合，从而得到整体电压序列的相似性。融入自适应分段云模型算法，以上5 种云模型相似性计算方法分别记为APLICM、AP-PCM、AP-ECM、AP-MCM 和 APOECM。结合附录B，对3.2 节中的标准化电压序列自适应分段云模型的结果进行相似性计算，结果见附录F。

分别采用加入自适应分段进行云模型相似度计算与不加入自适应分段的这几种算法，对13 个用户的相位连接关系识别结果如附录C 图C3 所示。由图C3 可得，自适应分段算法结合云模型算法，相别辨识准确率更高。

3.4 算法的准确性验证

本文通过定义有效性指标τ，自适应地确定电压序列需要分段的总数。本算例结果为台变相电压序列和用户电压序列分段总数均为3 时结果最优。为验证本文提出的有效性指标τ的准确性，本文先设置不同的分段总数，再对不同分段总数下的电压序列自适应地确定每段的起始时刻和结束时刻，以AP-ECM 算法为例，计算台变与用户电压序列的相似性结果，见附录G 表G1。

附录C 图C4 中以用户C1与C11为例说明不同分段总数下相别辨识结果的差异。图C4（a）中当分段总数为2 时，无法区分出用户C1属于A 相或是C 相；当分段总数为3 时，用户C1不仅与A 相的相似度最大，而且与其他相的相似度数值差异明显。当分段总数为4～11 时，三相的相似度数值相比于分段总数为3 时差异不明显，容易错判。同理可得，图C4（b）中当分段总数为3 时，用户C11的电压与台变A、B、C 三相电压的相似度数值差异最明显，相别辨识结果最准确。

综上所述，本节验证了在不事先指定电压序列的分段总数的前提下，所提出的有效性指标τ可以自适应地确定出最优的电压序列分段的总数，使得用户与A、B、C 三相电压的相似度计算数值差异最为明显，相别辨识结果更加准确。

3.5 SAPCM 算法与其他相似性算法的比较

采用其他相似性算法如PCC［8］、GRA［9］、DTW算法［12］和LR［16］分析计算用户电压与台变三相电压的相似度结果，见附录G 表G2 至表G5。可见，PCC、GRA、LR 和DTW 算法主要考虑电压序列的整体特征，在进行相别辨识时，由于台变三相电压接近，使得用户电压与台变相电压的相似度不具有区分度，相位关系容易误判。而本文所提出的SAPCM 算法将电压序列自适应分段，使得每个分段段内相似度高、段间相似度低。通过计算分段电压序列云模型的相似度得到电压序列间的相似度，克服了其他相似性算法在进行相别辨识时，数据区分度不明显的弊端。

用户相别辨识对实时性要求不高。尽管SAPCM 算法相较于其他相似性算法略显复杂且计算时间稍长，但准确率更高且更具有实用性。

4 SAPCM 算法的通用性分析

4.1 不同拓扑结构对算法的影响

低压配电网结构复杂多样。本算例通过MATLAB/Simulink 搭 建1 个 台 区 内15 个 用 户 的2 种不同拓扑结构的仿真模型，如图2 所示。

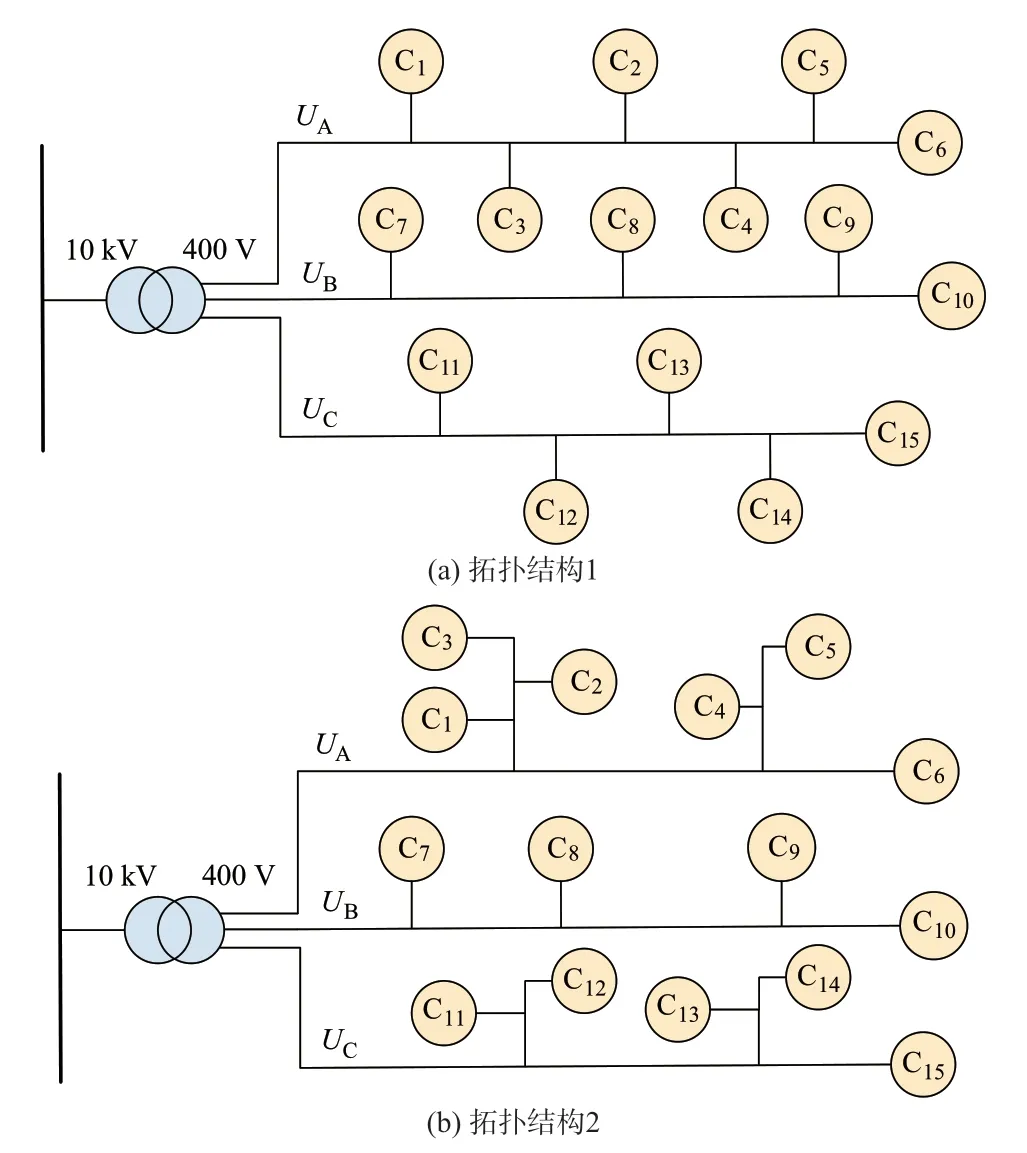
图2 低压配电台区拓扑仿真模型Fig.2 Simulation model for topology of low-voltage distribution station area

假定各用户功率在［2，4］kW 内随机变化，用户功率因数为0.90～0.95，采样周期为15 min，获得一天内台变和用户的电压序列。2 种拓扑结构中不改变15 个用户的负荷以及相别关系，仅改变台区的拓扑结构。

首先，根据获得的台变三相电压序列以及15 个用户的电压序列，采用SAPCM 算法自适应地确定电压序列的分段总数，得到2 种拓扑结构中18 个电压序列自适应分段的有效性指标τ与分段总数λ的关系见附录H 表H1 和表H2。其次，自适应地确定每一电压序列每一分段的起始时刻和结束时刻，见附录H 表H3 和表H4。最后，结合云模型的相似性算法分别计算表H3、表H4 中自适应分段电压序列云模型的相似性，得到的结果见表H5 和表H6。

由附录H 表H1 至表H4 可知，台区中不同拓扑结构下的电压序列自适应分段总数不同，并且每一分段的起始时刻和结束时刻也不同。但由表H5、表H6 可知，在不同拓扑结构下SAPCM 算法计算的结果表明，用户C1至C6的电压UC1至UC6与UA相似性高，故其连接在A 相；用户C7至C10的电压UC7至UC10与UB相 似 性 高，故 其 连 接 在B 相；用 户C11至C15的电压UC11至UC15与UC相似性高，故其连接在C 相，这与所搭建模型中用户相别关系一致。因此，本文算法在进行相别辨识时，不受台区拓扑结构的影响。

4.2 用户负荷对算法的影响

不改变图2（b）中的拓扑结构和用户相位连接关系，仅改变15 个用户的负荷，探究用户负荷变化对算法的影响，结果见附录H 表H7 至表H9。由表H9 可 知，用 户C1至C6连 接 在A 相，用 户C7至C10连接在B 相，用户C11至C15连接在C 相，这与所搭建模型中用户相别关系一致。

综上所述，不同的台区拓扑结构和不同的用户负荷会得到不同的台变相电压曲线和用户电压曲线。但是，SAPCM 算法可以根据设定的规则自适应地确定不同情况下电压序列的分段总数以及每一分段的起始时刻。因此，本文所提SAPCM 算法在进行相别辨识时，不受台区拓扑结构以及用户负荷的影响，具有较好的通用性。

4.3 SAPCM 算法的限制

当台变三相负荷完全平衡时，台变的三相电压完全一样，此时无论何种算法都无法确定用户相别关系。但在实际系统中，台变三相负荷的特性曲线不可能完全一致，这将导致三相的电压曲线存在差异。本文所提SAPCM 算法的优越性在于，当台变电压很接近时，算法仍具有很高的相别辨识准确率。

建立如图3 所示的仿真模型，台变每一相上只连接一个用户，且在开始时设定用户的负荷曲线相同。

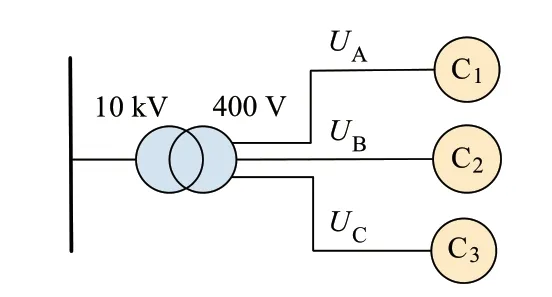
图3 简单拓扑Fig.3 Simple topology

分别在每一相的负荷曲线上加入不同的随机误差以模拟负荷的差异，在每种偏差情况下试验100 次，并在仿真得到的电压上增加[-0.1，0.1]V的随机数以模拟智能电表等计量设备的测量误差，统计出100 次试验中3 个用户相别关系均能被识别的准确率，结果如附录C 图C5 所示。结果表明，SAPCM 算法在电压差异很小时就能进行相别关系辨识，虽然相别辨识准确率不能达到100%，但其准确率明显高于PCC、GRA、DTW 和LR 算法。

4.4 低压配电台区中DG 接入对算法的影响

连接于低压配电台区中的DG 大多为单相发电系统，如光伏发电电源。由于DG 的不确定性与波动性，会对电网电压造成一定的影响。本节从以下2 个方面探究DG 的接入对本文所提算法的影响：一是DG 仅接入台区中某一相；二是DG 分散接入三相。

4.4.1 台区中某一相接入DG

在图2（a）中A 相接入一定数量的单相光伏电源，仿真得到15 个用户的电压和台变低压侧三相电压，再利用SAPCM 算法得到不同数量的光伏电源接入情况下用户电压与台变相电压的相似性结果，见附录I 表I1。由表I1 可得，在不同数量的光伏电源接入A 相的情况下，SAPCM 算法计算得到的相别关系依旧准确，且用户与台变不同相之间的相似度数值区分明显。

4.4.2 台区中三相接入DG

同理，在图2（a）中A、B、C 三相接入一定数量的单相光伏电源，得到用户电压与台变相电压的相似性结果见附录I 表I2。由表I2 可得，在不同数量的光伏电源分散接入台区三相的情况下，SAPCM 算法计算得到的结果仍然具有区分度，但受光伏电源的影响电压波动较大，用户与台变所属相的相关性会降低。

4.4.3 总结

以用户C2、C9和C15为例说明不同数量的光伏电源在不同的接入情况下，相别辨识结果受DG 的影响情况，如附录C 图C6 所示。由图C6 可得，当仅在A 相 接 入DG 时，随 着DG 数 量 的 上 升，UC2与UA、UC9与UB、UC15与UC的相似性结果数值很大，且基本稳定。在单相接入DG 时，会导致单相电压变化明显，使得三相电压的区分度更高。当DG 分散接入三相时，随着DG 数量的上升，UC2与UA、UC9与UB、UC15与UC的相似性结果数值逐步降低。但当配电网规模小、接入DG 少时，从用户电压与3 个相电压的相似性数值大小比较依旧可以得到准确的相别辨识结果。

5 观测误差与观测非同时性的影响分析

观测误差是智能电表电压测量值的误差，一般由系统误差和随机误差2 个部分构成：系统误差是由于智能电表本身的特性决定的，相对稳定不变；随机误差是由于一些不稳定的随机因素造成的，其数值相对系统误差更小。

5.1 系统误差对算法的影响

目前家用智能电表等级为0.5 级或更高，即误差小于0.5%，老式电表误差相对更大，可按1%考虑。

搭建如图2（a）所示的仿真模型，为方便说明，忽略台变相电压系统误差，各用户的系统误差在[-2.2，2.2]V（220 V×1%=2.2 V）范围内变化。采用本文所提SAPCM 算法计算每次系统误差变化后用户电压与台变相电压的相似性结果，最终计算结果均与附录H 表H5 一致。

采用SAPCM 算法对电压数据进行Z-score 标准化处理，可以排除由于智能电表系统误差引起的电压数据变化的影响，因此，电表系统误差对本文算法没有影响。

5.2 随机误差对算法的影响

同理，在图2（a）的仿真模型中，忽略台变相电压随机误差，分别令用户电压的随机误差取±0.1、±0.2、±0.3、±0.4、±0.5、±0.6、±0.7、±0.8、±0.9、±1.0 V 的随机值时，对上述每一种误差情况仿真100 次，得到不同随机误差下基于SAPCM 算法的15 个用户的相别辨识结果准确率，见附录J表J1。

以用户C4、C6、C10和C12为例说明随机误差对算法的影响，如附录C 图C7 所示。可见，随着随机误差的增大，采用本文所提SAPCM 算法进行相别辨识的准确率也会下降。随机误差不可避免，但从随机误差的统计规律可知，绝对值小的误差出现概率很大，占绝大多数。在随机误差绝对值较小时，本文算法依旧可以保持较高的准确率。

5.3 观测非同时性对算法的影响

为仿真分析观测非同时性对算法的影响，每台电表设置一个固定同步时间误差，即偏离标准时间0～5 min，各电表的随机时间误差在微秒级，可忽略不计。

搭建如图2（a）所示的仿真模型，假设台变智能终端无同步时间误差，15 台用户智能电表的固定同步时间误差随机设置为0～5 min，仿真10 次，得到基于SAPCM 算法的15 个用户的相别辨识结果，见附录J 表J2。可见，台区中智能电表设置不同的同步时间误差，进行多次仿真后，15 个用户的相别辨识结果依旧准确。各智能电表同步时间误差设定后，对于同一电表所有采样点均具有相同的时间误差，且这个时间误差较小，电压变化很小。因此，本文所提SAPCM 算法基本不受观测非同时性的影响。

6 结语

针对低压配电台区单相用户相别辨识问题，本文提出了基于自适应分段云模型的相别辨识方法。该方法具有以下特点：

1）采用云模型处理电压时间序列，一方面对电压序列进行降维，另一方面采用云模型的数字特征反映出电压序列的分布特征；

2）自适应分段云模型算法无须事先指定分段的个数，既可以自适应地确定电压序列的分段总数，又可以自适应地确定每个分段的起始时刻和结束时刻，体现出电压序列的分段特征；

3）采用自适应分段云模型算法进行相别辨识时，不受台区拓扑结构以及用户负荷的影响，在大多数情况下，辨识准确率高，具有较好的通用性；

4）自适应分段云模型相似度算法将一个电压序列表示成若干个正态云，通过计算分段云模型的相似度来替代整体电压序列的相似度，充分考虑到电压序列的局部特征，解决了现有相似度算法在处理相别关系时数值区分度不明显且容易误判的问题；

5）利用历史电表电压数据对低压台区拓扑结构进行辨识，无须新增设备，在减少投资的同时减轻了运行人员的劳动强度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。