圆柱曲面单光子量子雷达散射截面的理论研究*

田志富 吴迪 胡涛

(中国人民解放军战略支援部队信息工程大学,数据与目标工程学院,郑州 450000)

为研究圆柱曲面的单光子量子雷达散射截面与经典雷达散射截面相比存在的具体优势,引入光子波函数,将引起量子干涉的距离矢量进行分解,通过圆柱曲面的曲面积分推导得到了单基地单光子下的圆柱曲面量子雷达散射截面的封闭表达式.分析了不同电尺寸的圆柱曲面长度和曲率半径的影响,对比了圆柱曲面量子雷达散射截面与经典雷达散射截面的封闭表达式.封闭表达式的分析和仿真结果都表明,圆柱曲面长度的电尺寸决定量子雷达散射截面的旁瓣数,曲率半径的电尺寸决定了量子雷达散射截面曲线的包络,量子雷达散射截面的整体强度与曲率半径的电尺寸呈线性关系.圆柱曲面的量子雷达散射截面与经典雷达散射截面相比具有旁瓣增强的优势,有利于隐身目标的探测.

1 引言

量子雷达可以实现极高的探测灵敏度和超越标准量子极限的分辨率[1,2],拥有稳定地探测隐身飞行器的可能性.这种可能性从根本上取决于发射光子和目标的相互作用.量子雷达散射截面(QRCS)是衡量在量子雷达照射下目标散射特性的基本参数,与目标结构和材料、入射光子数、入射光子频率和光子入射方向等密切相关.

研究人员分析了矩形、三角形和圆形等平板物体的QRCS[3-10],通过解析表达式证明了量子雷达探测这些目标可能存在旁瓣优势和多光子优势.这些优势被证明在单基地和双基地量子雷达中都是存在的[8,9].研究人员也通过数值模拟得到了球体、长方体、圆柱体、圆锥体和四棱锥等三维目标的QRCS 曲线[11-16],但是没有给出更多的信息.QRCS计算中的数值模拟指的是在仿真中设置目标表面原子间距,对目标表面原子进行采样,利用光子与采样位置处的原子的相互作用得到光子波函数,干涉得到QRCS 图样的方法.因此数值模拟适用于任何形状目标的QRCS 计算仿真,但是存在计算量大和随原子采样间隔增大而增大的计算误差的问题.QRCS 的封闭表达式是对QRCS 计算式中目标表面原子位置进行连续化积分处理后得到的解析解,能够有效解决计算量和计算精度之间的矛盾问题,同时解析解中物理量的数量关系清晰明确,但是复杂形状结构目标的QRCS 中的积分很难计算出来.目前还不了解三维物体是否也存在旁瓣优势以及更加具体的数量关系等情况,需要进一步的研究.

选取圆柱曲面作为研究对象,因为目标物体中圆柱曲面的常用性,特别是在飞行器和导弹中圆柱曲面更是作为结构主体存在.同时圆柱曲面不同于棱柱和棱锥等可视为平板复合的三维物体,圆柱曲面是典型的光滑曲面物体.所以以圆柱曲面为研究对象,研究圆柱曲面单光子QRCS 的封闭表达式具有重要的意义.

在圆柱曲面QRCS 数值模拟[11-13]的基础上,推导了圆柱曲面QRCS 的封闭表达式,并与数值模拟结果[11,13]对比验证了其有效性.将封闭表达式拆分为周期变化项和曲线包络项,详细分析了圆柱曲面不同电尺寸长度和曲率半径对QRCS 的影响.并与利用物理光学法推导的经典雷达散射截面(CRCS)封闭表达式进行了比较分析.

2 圆柱曲面单光子QRCS 封闭表达式原理

类比于CRCS,QRCS 被定义为[3]

图1 圆柱曲面的几何结构Fig.1.Geometry of cylindrical surface.

式中,A⊥(θ,φ)为物体垂直于入射场方向的投影面积,N为圆柱曲面表面被照亮原子数,ΔRn表示物体表面原子与雷达之间的距离,k为波数.

从(2)式可知,单光子QRCS 的结果由散射的概率波在空间上干涉决定.不同物体结构散射的概率波的干涉距离不同,这是导致干涉图样不同的关键.在图2 的圆柱曲面表面原子到雷达矢量的分解示意图中,x′为圆柱曲面散射点的位置矢量,x为圆柱曲面散射点到雷达的矢量,d为雷达到物体中心的矢量.则被雷达照亮曲面的原子散射波的干涉距离有以下分解:

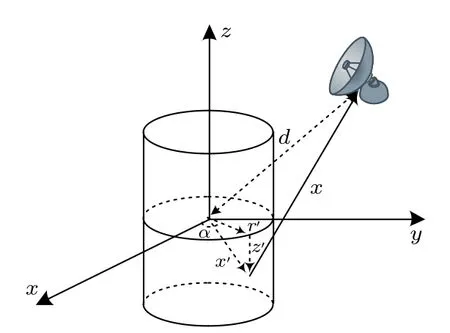
图2 在圆柱曲面表面原子到雷达矢量的分解示意图Fig.2.Schematic diagram of atom-to-radar vector decomposition on cylindrical surface.

从(3)式可以知道,同一物体的各面元表面散射单元有相同的常数项 exp(jKd),所以造成量子干涉差异性的主要原因在于曲面散射点的位置矢量的不同.将(2)式中的求和转化为积分,消去相同的常数项,得到

式中K为散射波矢量与入射波矢量之差.根据圆柱体的对称结构,设θ ∈(0,90°),φ=0°.(4)式中的曲面积分为

式中,对于单基地量子雷达,Kr=2kcos(θ),Kz=2ksin(θ).进一步有

进而(4)式的分母可以写为

式中,

其中,λ为入射波波长,χ(k,r,l)是l/λ和r/λ的函数.当r/λ一定时,(9)式的积分收敛为常数[4,8].因此,(9)式可以进一步化简为

另外,远场条件下,有

将(7)式、(8)式、(10)式和(11)式代入(4)式,圆柱曲面QRCS 的封闭表达式为

3 结果与讨论

3.1 验证

目前还没有性能足够的量子器件进行相应的探测实验.我们通过仿真实验呈现封闭表达式的结果.仿真实验中,入射光子波长为0.03 m,圆柱面的长度l=6λ,曲率半径r=λ,圆柱面表面原子间距δ=0.04λ.图3 表明我们推导的解析式的结果与文献数值模拟的结果[11,13]基本吻合,大角度处微小的差异是数值模拟中原子采样的缘故[4].

图3 封闭表达式计算和数值模拟的圆柱曲面QRCSFig.3.The QRCS of closed-form expression and numerical calculation for cylindrical surface.

3.2 不同电尺寸长度的QRCS

不同电尺寸的圆柱曲面将呈现出不同的QRCS特性.在3.1 节仿真的基础上,设置圆柱曲面长度l分别为 2λ,3λ,4λ,结果如图4.

图4 不同电尺寸圆柱曲面长度的QRCSFig.4.The QRCS of cylindrical surfaces with the lengths of different electrical sizes.

分析(12)式,当θ=0°时,主瓣峰值与曲面长度l的平方成正比.旁瓣数量为 4l/λ-2 .图4 印证了与曲面长度相关的这些特性.这些特性使得量子探测有了具体数量的指标.

特别地,发现图4 中QRCS 的旁瓣包络随曲面长度l的增加几乎没有变化.分析圆柱曲面QRCS的解析式,将(12)式分为和σ2=sin2(klsin(θ)),其中σ1为QRCS 的包络曲线项,σ2为QRCS 的周期变化项,如图5 所示.从解析式看包络σ1与曲面长度l无关.所以曲面长度只会影响θ=0°时的峰值高度和旁瓣数,对于旁瓣的强度没有影响.这意味着圆柱目标的长度变长,即被照亮的区域变大,对于量子探测也不会产生增益,这为隐身目标的结构设计提供参考.

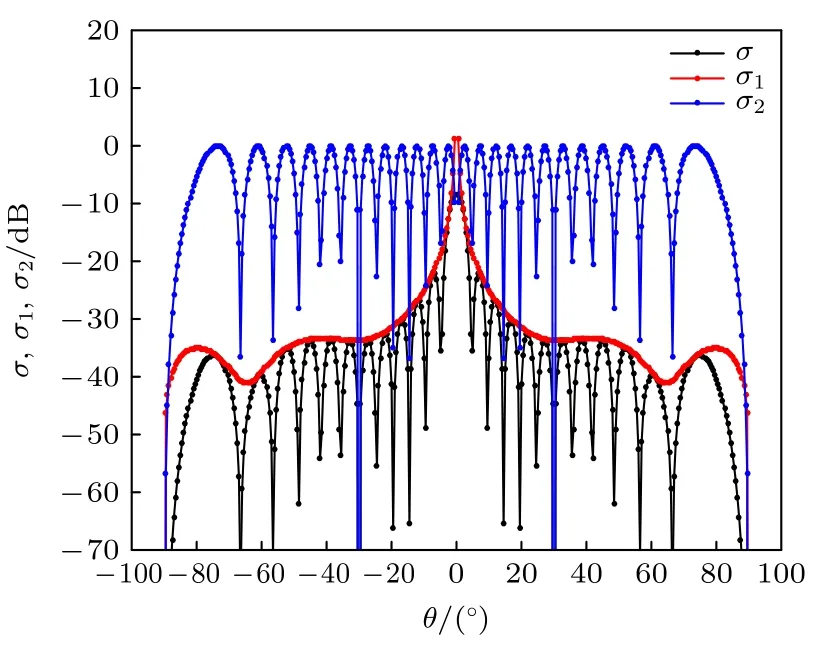
图5 圆柱曲面QRCS 曲线及其包络曲线和周期变化曲线Fig.5.The QRCS of cylindrical surface and its envelope curve and periodic change curve.

3.3 不同电尺寸曲面半径的QRCS

为了直观地了解曲面曲率对QRCS 的影响.在3.1 节仿真的基础上,设置圆柱曲面半径r分别为λ,10λ,50λ,结果如图6 所示.

图6 不同电尺寸圆柱曲面曲率半径的QRCSFig.6.The QRCS of cylindrical surfaces with the curvature radii of different electrical sizes.

解析式(12)和图6 表明QRCS 整体与曲率半径基本呈线性关系.将σ1中的线性r项去掉,分析曲率半径对于包络的影响,如图7 所示.可以看出曲率半径对于QRCS 的影响,除了线性关系之外,还会使得QRCS 曲线增加更多细微的波动,这是电大尺寸目标QRCS 的特性.可见,与曲率半径电尺寸相关的η(θ,r/λ)项对QRCS 包络影响较小且对整体强度几乎没有影响.比较曲面长度和曲率半径对QRCS 的影响,曲面长度变长不会对单光子量子雷达的探测产生较大影响,而曲率半径变大则会使得QRCS 整体变大.这为量子探测圆柱曲面提供了重要的依据.

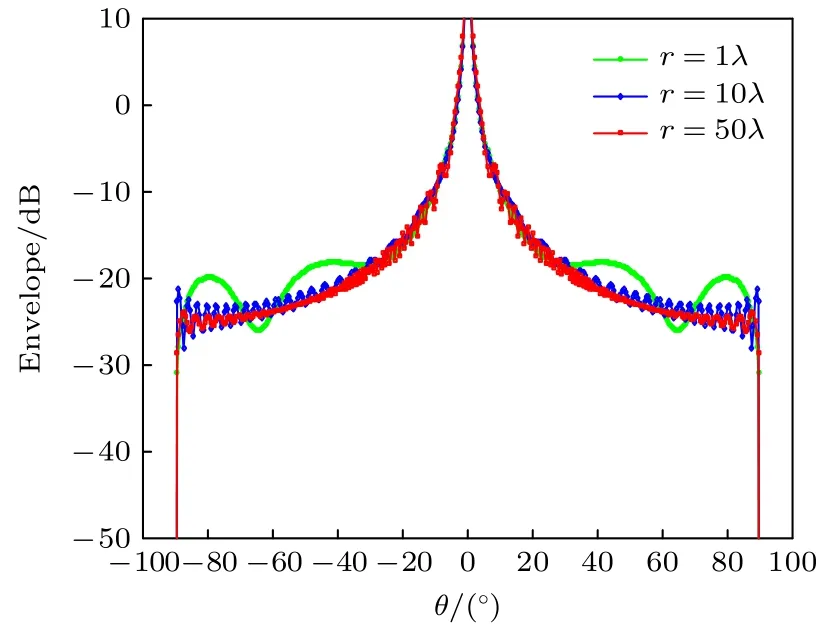
图7 不同电尺寸圆柱曲面曲率半径的QRCS 包络曲线Fig.7.Envelope curves of the QRCS of cylindrical surfaces with the curvature radii of different electrical sizes.

3.4 与CRCS 比较

根据物理光学法,圆柱曲面的CRCS 为

在3.1 节仿真的基础上,利用(12)式和(13)式得到圆柱曲面的QRCS 和CRCS 如图8 所示.从图8 可以看出,二维平板类目标可能存在的旁瓣优势在圆柱曲面目标中也存在.且对比(12)式和(13)式,这种旁瓣优势的数量关系同样源于 cos(θ)对cos2(θ)的优势[4].这种单光子探测下的旁瓣优势有利于隐身目标的探测.QRCS 和CRCS 的本质不同,QRCS 源于光量子概率波函数带来的不确定性形成的干涉.量子雷达利用光子与原子相互作用,可对目标的不同的原子结构产生不同的响应.而CRCS 源于目标表面感生电流的响应.当光量子数增大到一定的数量,QRCS 与CRCS 趋于一致.因此,目前针对经典探测的隐身技术大多对量子探测并不会产生影响,量子探测技术具有探测隐身目标的潜力.

图8 圆柱曲面QRCS 与CRCS 的对比Fig.8.Comparison between the QRCS and the CRCS of cylindrical surfaces.

4 结论

利用矢量分解,推导了单基地下的圆柱曲面单光子QRCS 的封闭表达式,为单光子探测提供具体的数量参考.对不同电尺寸的圆柱曲面长度和曲率半径进行分析,发现圆柱曲面长度的改变只对入射角度为0°时的QRCS 产生影响,对其他角度的QRCS 没有影响,而曲率半径的改变会使得QRCS整体强度改变.这对隐身目标的设计提供思路.对比圆柱曲面的QRCS 与CRCS,证实单量子探测圆柱曲面也存在旁瓣优势.量子雷达可以实现高灵敏度和超越标准量子极限的探测,具有探测隐身目标的潜力.所有的分析都忽略了衍射和吸收作用的影响,这方面研究有待进一步开展,同时实际自由空间的探测实验还有很长的路需要走.