旋翼翼型高维多目标气动优化设计

宋超，周铸，李伟斌，罗骁

（中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000）

旋翼是直升机的核心气动部件，旋翼气动设计技术为直升机平台性能提供坚实的支撑［1］。旋翼翼型是旋翼气动设计的基础，直接影响直升机的飞行包线、载荷、噪声等关键指标，其复杂的工作状态决定了翼型设计是一项十分复杂的工作。旋翼桨叶之间存在强烈的气动干扰，且展向剖面翼型相对气流速度受高速旋转而差别巨大。在直升机飞行的不同工况下，前飞速度与旋转速度叠加，使得旋翼在不同方位角的工况也剧烈变化。例如，在前飞时，前行桨叶桨尖区域上存在跨声速流动，伴随激波的产生；在机动飞行时，旋翼后行桨叶上存在分离或动态失速现象。因此，先进的旋翼翼型要求兼顾高速低阻、低速高升力、低零升力矩等特性［2］，其设计是典型的多设计点、多目标和强约束优化问题。

基于数值优化方法的翼型设计技术已经取得了很大进步，但如何满足多设计点、多目标、多约束的设计要求，仍是亟需突破的难点。对于多目标优化问题，常见的做法是采用目标加权方法将多目标统一为单目标。例如，杨慧等［3］在开展旋翼翼型多目标、多约束设计时，将悬停状态阻力、机动状态升力、阻力发散马赫数特性等多设计目标加权统一为单目标问题。王清和招启军［4］提出了适用于中型运输直升机旋翼翼型设计的目标及约束条件，利用遗传算法对SC1095翼型进行了优化，也将多个设计目标组合为单一目标。

目标加权方法的优化结果依赖于权因子的选取，当优化目标较多时，选取合适的权因子是十分困难的。采用基于Pareto非支配关系的多目标进化算法，如NSGA-Ⅱ，可以得到整个Pareto最优前沿，以供设计者决策。Wang和Zhao［5］采用NSGA-Ⅱ算法进行了考虑2个设计点的旋翼翼型设计，旨在提高翼型升阻特性。Massaro和Benini［6］以SC1095翼型为基准，利用进化算法与代理模型进行了旋翼翼型两目标的设计，得到了最优Pareto前沿。然而，进化多目标算法解决高维多目标设计问题（目标数大于3）时面临难以收敛的挑战。具体而言，随着目标数的增多，Pareto占优关系难以区分进化个体，进化动力不足，描述Pareto前沿的解集数目也呈指数级增长，算法收敛缓慢，甚至难以收敛。为了避免高维多目标优化问题面临的收敛困难问题，Zhao等［7］利用主成分分析（principal component analysis，PCA）降维方法，将6个目标的旋翼设计问题转化为2个目标设计问题。然而，多目标自身相关的严苛要求和降维对结果的不确定影响，使得降维方法的应用受到了一定限制。

在进化算法研究领域，解决高维多目标优化算法难以收敛的问题也是热点之一。Deb和Jain［8］利用聚类算子替换了NSGA-Ⅱ中的拥挤距离算子，提出了NSGA-Ⅲ算法，能够有效应用于高维多目标优化问题。Zhang和Li［9］提出了一种基于分解的多目标优化算法（multi-objective evolutionary algorithm based on decomposition，MOEA/D），其优越的性能受到了学者们的广泛关注。利用高维多目标优化算法，能够充分考虑复杂气动优化所涉及的多个目标，有助于提高综合气动性能。然而，该类算法对复杂气动优化设计问题的适应性还未得到验证。

高维多目标优化设计面临的另一个挑战是目标空间的可视化问题。由于目标空间维数的增加，Pareto前沿难以在二维或三维坐标系中直观展现。高维目标空间的可视化也是亟待解决的问题与研究的热点。高维目标空间可视化技术可分为2类：①在平行坐标系中表示目标的解，如热图［10］和平行坐标系［11］；②构建高维到二维的映射关系，并保留解之间的距离信息，如自组织图映射（self-organizing mapping，SOM）［12］、径向坐标可视化［13］、雷达图［14］等。SOM方法凭借其直观的解集性质表达形式，成为了目前流行的可视化方法。Kumano等［15］采用多目标遗传算法进行了涉及4个目标的公务机机翼气动/结构多学科优化，并利用SOM 对最优Pareto前沿进行了可视化分析。王超［16］利用SOM对旋翼翼型与战斗机翼型最优Pareto前沿进行了聚类分析，为设计决策提供了全局视角。

为实现旋翼高维多目标气动优化设计，提高旋翼翼型综合气动特性，基于MOEA/D算法建立了考虑高低速升阻特性、力矩特性、阻力发散特性等的旋翼翼型高维多目标优化设计方法，并采用高精度kriging模型以提高优化设计效率。采用SOM方法对最优解集进行了聚类分析，并对典型最优翼型进行了验证与分析。

1 高维多目标优化设计框架

针对旋翼翼型的高维多目标优化设计问题，本文采用MOEA/D算法进行问题求解。算法在优化过程中需要计算大量的种群，对利用高精度CFD分析的优化问题，需要耗费巨大的计算资源。本文利用kriging模型，建立设计变量与气动特性之间较为精确的模型，以代替耗时的高精度CFD分析。本节简略介绍MOEA/D算法与kriging代理模型。

1.1 MOEA/D算法

MOEA/D算法并不直接近似Pareto前沿，而是将多目标优化问题分解成一定数量的单目标优化子问题，然后利用进化算法同时求解这些单目标子问题。这些单目标最优解集的集合是真实Pareto前沿面的一个良好近似。每个单目标子问题通过初始权向量之间的距离组成邻域，子问题在对应的邻域内与其他子问题进行协同优化。一般可以采用加权函数、Tchebycheff函数、基于惩罚的边界交叉（penalty-based boundary intersection，PBI）等方法将多目标转换为单目标求解。本文采用Tchebycheff函数聚合方法，其数学表达式为

式中：x为决策变量；z*=为参考点；为权重向量，共有N组权重向量。

采用Das-Dennis方法［17］生成指定数量的相对均匀的权重向量，它们同时满足如下条件：

式中：H为用户定义的正整数；权重向量个数（种群个数）满足。

下面简单描述MOEA/D算法步骤：

步骤1算法初始化。

构造权重向量λ1，λ2，…，λN，并计算任意2个权重向量之间的欧氏距离，为每个权重向量选出最近的T个向量作为它的邻域B（i）=｛i1，i2，…，iT｝。

初始化种群x1，x2，…，xN，设FVi=F（xi），i=1，2，…，N。

初始化z=（z1，z2，…，zk），zj=），其中j=1，2，…，k。

步骤2更新。

繁殖：从B（i）中选择2个个体r1、r2，利用xr1、xr2交叉生成新的个体¯y，再以一定的变异概率生成y。

修正：在y的基础上应用特定的修正或启发式改进策略，得到新的个体y′；若fj（y′）＜zj，则zj=fj（y′），j=1，2，…，k。

步骤3停止判断。若满足停止条件，算法停止，输出Pareto前沿，否则执行步骤2。

1.2 kriging模型

kriging模型是一种基于随机过程的估计方差最小无偏估计模型，适用于拟合具有高度非线性、多峰值问题，在气动优化设计领域中有广泛的应用。随机函数Y（x）定义为

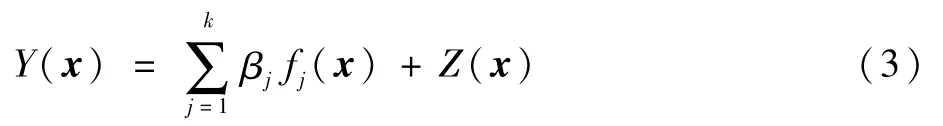
式中：fj（x）为基函数，一般可选为简单的多项式；βj为基函数对应的系数；代表Y（x）的数学期望值；Z（x）为均值为0、方差为的静态随机过程。对于设计空间中的任意2个位置x与x′，随机量的协方差可表述为

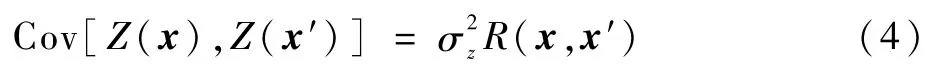
式中：相关函数R（x，x′）只与空间距离有关，代表了不同位置随机变量之间的相关性，相关函数在两位置距离无穷大时R=0，距离为零时R=1；R随距离的增大而减小。

本文选用常用的高斯函数：

式中：θ为kriging超参数，本文采用最大似然估计方法训练得到θ。

采用交叉验证（leave-one-out）方法来验证kriging模型精度，定义为

式中：y（xi）为第i个样本点的响应值；y-（i）（xi）为xi的预测值，特殊之处在于该预测值是由利用排除第i个样本点之后的样本集所建立模型的预测值。

2 求解器精度验证

进行旋翼翼型气动优化设计研究前，先验证求解器的精度。气动特性求解采用PMB3D［18］。求解RANS方程所采用的时间推进方法为LU-SGS，空间离散采用JST格式。湍流模型为Spalart-Allmaras模型。计算网格为C型结构网格，网格示意图如图1所示。

图1 OA309翼型计算网格Fig.1 Computational grids for OA309 airfoil

为排除计算网格对结果的影响，开展网格无关性检验，选取3套网格作为检验对象。表1为不同网格量对应的升力系数Cl和阻力系数Cd。计算状态为Ma=0.6，Re=2.5×106，Cl=0.50。从表中可以看出，3组不同网格量计算得到的升力系数几乎一致，阻力系数随网格量的增大而减小，其中网格2与网格3的阻力系数仅相差0.67%。因此，兼顾网格规模和计算精度考虑，选用网格2进行流场分析。

表1 OA309翼型气动特性随网格量的变化Table 1 Aerodynamic performance of OA309 airfoil with different amounts of computational grids

为验证求解器的可靠性，进行了OA309翼型不同状态下计算值与实验值的对比。实验值来自西北工业大学翼型叶栅空气动力学国防科技重点实验室NF-6风洞，实验雷诺数表示为Re=Ma×4.2×106。图2为OA309翼型表面压力分布计算值与实验值对比（Ma=0.6，Re=2.5×106，Cl=0.6），计算值在压力峰值处略小于实验值，两者总体吻合良好（Cp为表面压力系数）。图3为相同状态下OA309翼型极曲线的计算值和实验值对比，可以看出两者的阻力值吻合良好。在Cl=0.5时，阻力计算值相比实验值的计算误差约为6.4%。由此可以看出，PMB3D计算结果能够很好反映翼型的气动特性。

图2 OA309翼型表面压力系数分布计算值与实验值对比（Ma=0.6，Re=2.5×106，Cl=0.6）Fig.2 Comparison of pressure coefficient at surface between numerical results and experimental data for OA309 airfoil（Ma=0.6，Re=2.5×106，Cl=0.6）

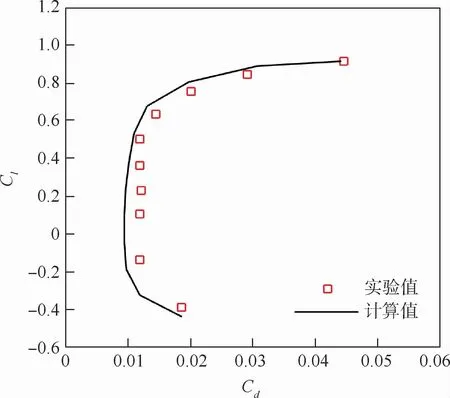
图3 OA309翼型极曲线计算值与实验值对比（Ma=0.6，Re=2.5×106）Fig.3 Comparison of polars between numerical results and experimental data for OA309 airfoil（Ma=0.6，Re=2.5×106）

3 旋翼翼型高维多目标算例

旋翼不同站位的翼型流场环境随旋翼工作状态和旋翼方位角的变化而剧烈变化，因此，旋翼翼型的设计需要充分考虑其站位的不同。一般将旋翼翼型划分为外段翼型（90%R～100%R，R为旋翼半径）、中段翼型（80%R～90%R）和内段翼型（75%R～80%R）。外段翼型强调高速性能；内段翼型强调高升力性能；中段翼型则兼顾两方面性能。然而，旋翼翼型设计指标之间往往相互矛盾、相互制约，需要根据直升机性能需求确定设计目标，通过仔细地权衡和折中，在上述要求中取得一个较好的平衡。

本文充分考虑旋翼翼型的各项性能指标，提炼出高维多目标设计优化问题，避免了设计目标难以权衡的问题。下面分别以布置在中段的9%厚度翼型和内段的12%厚度翼型为例，进行旋翼翼型高维多目标优化。

3.1 9%厚度旋翼翼型高维多目标算例

以OA309翼型为初始翼型，翼型参数化采用CST（class function/shape function transformation）方法［19］，翼型上下表面型函数阶数均为6，设计变量数目为14。以OA309翼型的CST参数为基准，设计变量变化范围为±20%。

旋翼设计同时考虑高升力能力、悬停效率和阻力发散特性，具体的设计目标和约束条件如表2所示。Ma=0.4时的最大升力系数是衡量旋翼翼型性能的重要参数，同时需要考虑Ma=0.4时的力矩特性，对应于表中的前2个设计目标。Ma=0.6时，机动状态需要较大的最大升力系数，对应表2中设计目标3；在Ma=0.6时，为悬停状态，为了提高悬停效率，需要减小翼型阻力，对应设计目标4。最后，考虑阻力发散特性，同时约束力矩系数的绝对值。本设计问题的设计目标个数为5，几何约束与力矩约束共5个，涉及的计算状态共7个。定义多目标设计问题为

表2 9%厚度旋翼翼型设计目标与约束Table 2 Design objectives and constraints for a r otor airfoil with 9% thickness

式中：对5个设计目标进行了归一化处理，参考值为OA309翼型的性能；下标数字对应设计状态；设计状态5、6、7对应的马赫数分别为0.80、0.81、0.82，Re=Ma×8×106；上标0表示基准翼型；A为翼型面积；t为翼型最大相对厚度；Cm为力矩系数。

根据设计问题，采用进化算法开展优化设计，需要大量评估翼型的气动性能，而高精度CFD流场分析耗时耗力。为提高优化效率，采用kriging模型建立气动特性的响应模型，替代优化过程中的流场计算。首先，采用拉丁超立方试验设计方法（latin hypercube sampling，LHS）［20］生成700个样本点，在7个给定的设计状态下进行翼型气动特性分析。进而采用交叉验证方法检验模型精度。以设计状态1为例，在700个样本点中随机抽取1个样本点进行交叉验证，重复进行10次，得到的最大预测误差与平均预测误差如表3所示。从表中可以看出力矩系数的预测误差相对较大，但最大预测误差仅为2.596%，阻力系数预测误差保持在0.2%以下，升力系数预测更为准确。交叉验证结果表明，kriging模型具有较高的预测精度，可以替代高精度的CFD流场分析。

表3 设计状态1的kriging模型交叉验证结果Table 3 Results of cross validation for kriging model under design condition 1

在建立了高精度kriging模型之后，利用kriging模型进行5目标的全局优化设计。首先，采用MOEA/D算法，参数设置采用Das-Dennis方法：H=9，得到权重向量个数为715，邻居子问题规模为20，交叉概率为0.5，最大迭代步数为200步。

图4给出了优化迭代200步后的Pareto前沿。从图中可以看出，f1与f4、f1与f5存在较为明显的非支配关系，然而f1与f2、f3的支配关系不明显。类似图4的二维图像不能很好表达设计目标之间的关系，很难从中选择出综合性能良好的设计结果。

图4 旋翼翼型优化最优Pareto前沿Fig.4 Optimal Pareto front for optimization of rotor airfoil

本文采用SOM处理最优Pareto前沿，选取的SOM单元个数为6×6。SOM 聚类分析将每组目标视为一个个体，根据个体之间的距离将715组5维目标映射在36个单元上，处理后的结果如图5所示。比较图5（a）与图5（d），图5（a）中深色区域基本对应图5（b）中浅色区域，反映出目标1与目标4是相互矛盾的，这也与图4中反映的趋势一致，说明了SOM 聚类分析的正确性。图5（f）为每个SOM 单元包含的个体数，综合图5（a）～（e），折中选取图5（f）亮黄色单元中的个体进行分析。表4中给出了亮黄色单元中的8组目标，可以看出8组最优目标具有高度相似性，其中目标1和目标4与基本翼型基本保持一致，目标3略有下降，目标2和目标5提升明显。下面选取其中第1个个体，并利用CFD进行气动特性分析。

图5 最优Pareto前沿SOM可视化结果（9%厚度翼型）Fig.5 Visualization results of optimal Pareto front using SOM（airfoil with 9% thickness）

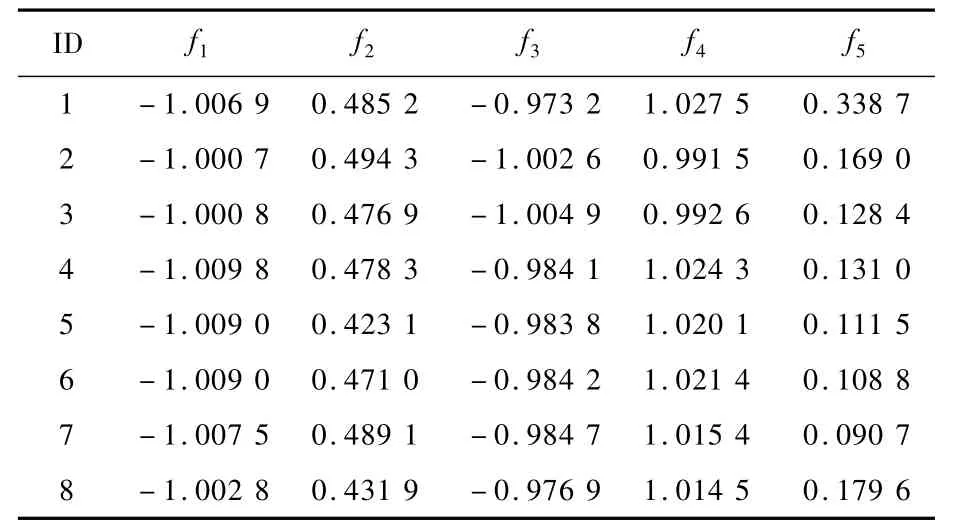
表4 Pareto前沿中选取的8组最优目标Table 4 Eight groups of optimal objectives selected from Pareto front

图6为选取的优化翼型形状，表5为优化翼型与OA309翼型的几何信息，包括最大相对厚度与翼型面积，从表中可以看出，优化翼型的相对厚度与无量纲面积均满足约束条件。

表5 OA309翼型与优化翼型几何信息Table 5 Geometry information of OA309 and optimized airfoils

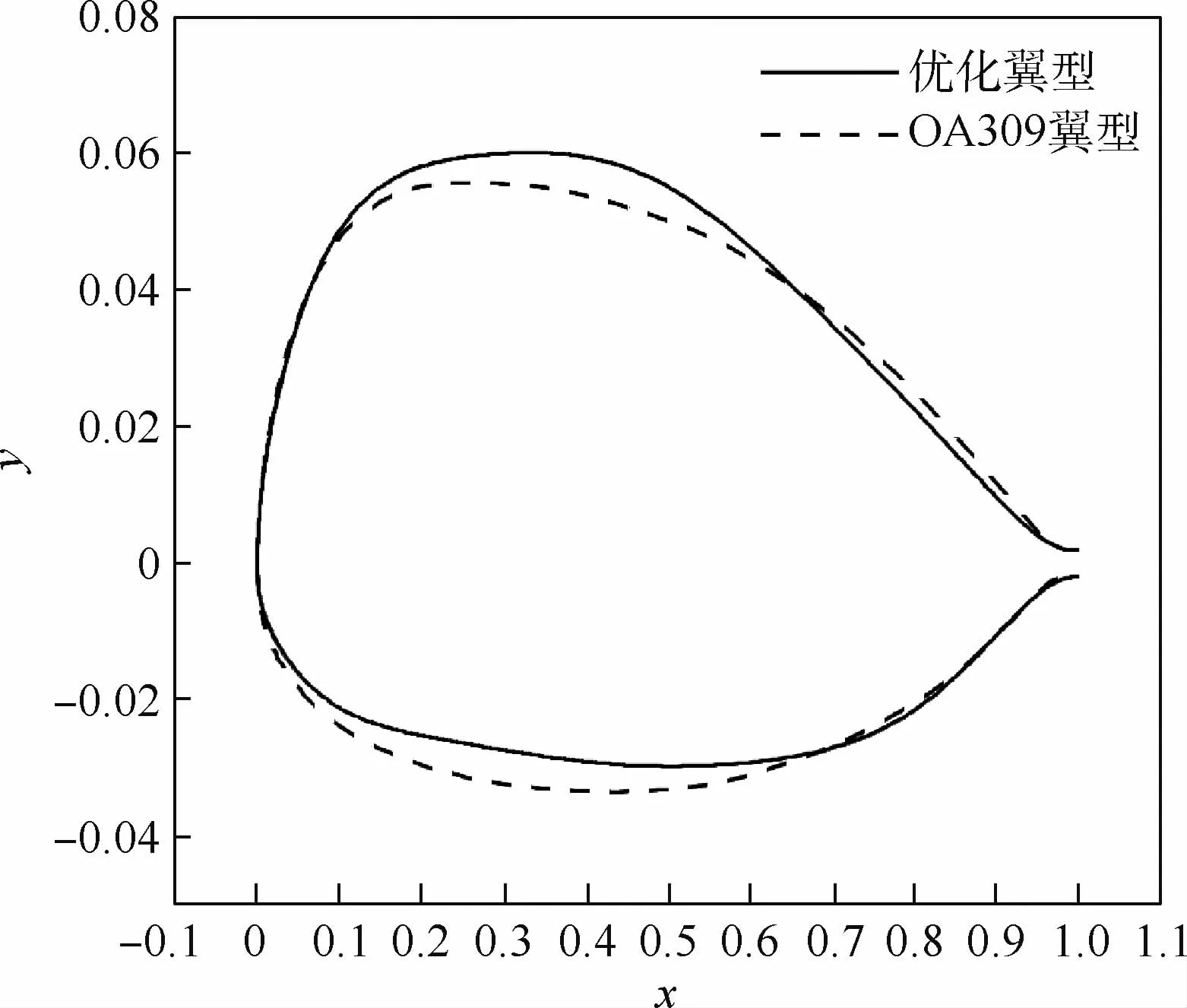
图6 OA309翼型与优化翼型形状Fig.6 Geometry shape of OA309 and optimized airfoils

优化翼型与OA309翼型的升阻特性对比如图7所示，可以看出，优化翼型与OA309翼型在Ma=0.4时的升阻特性基本一致。图8给出了Ma=0.4时的力矩特性。可以看出，优化翼型的零升力矩绝对值相比OA309翼型基本不变，在更大的升力系数范围内，优化翼型相比OA309翼型的力矩系数更接近0，力矩系数幅值（Cl≈0.8）减小约50.7%，力矩特性得到改善。在高马赫数Ma=0.6时，气动特性可以由图9、图10中看出，高马赫数下的最大升力系数和最大升阻比均有明显提高，其中最大升力系数提高约6.5%，最大升阻比提高约7.7%。对于力矩特性，优化翼型在较大范围具有更小的力矩幅值，力矩特性得到提升。

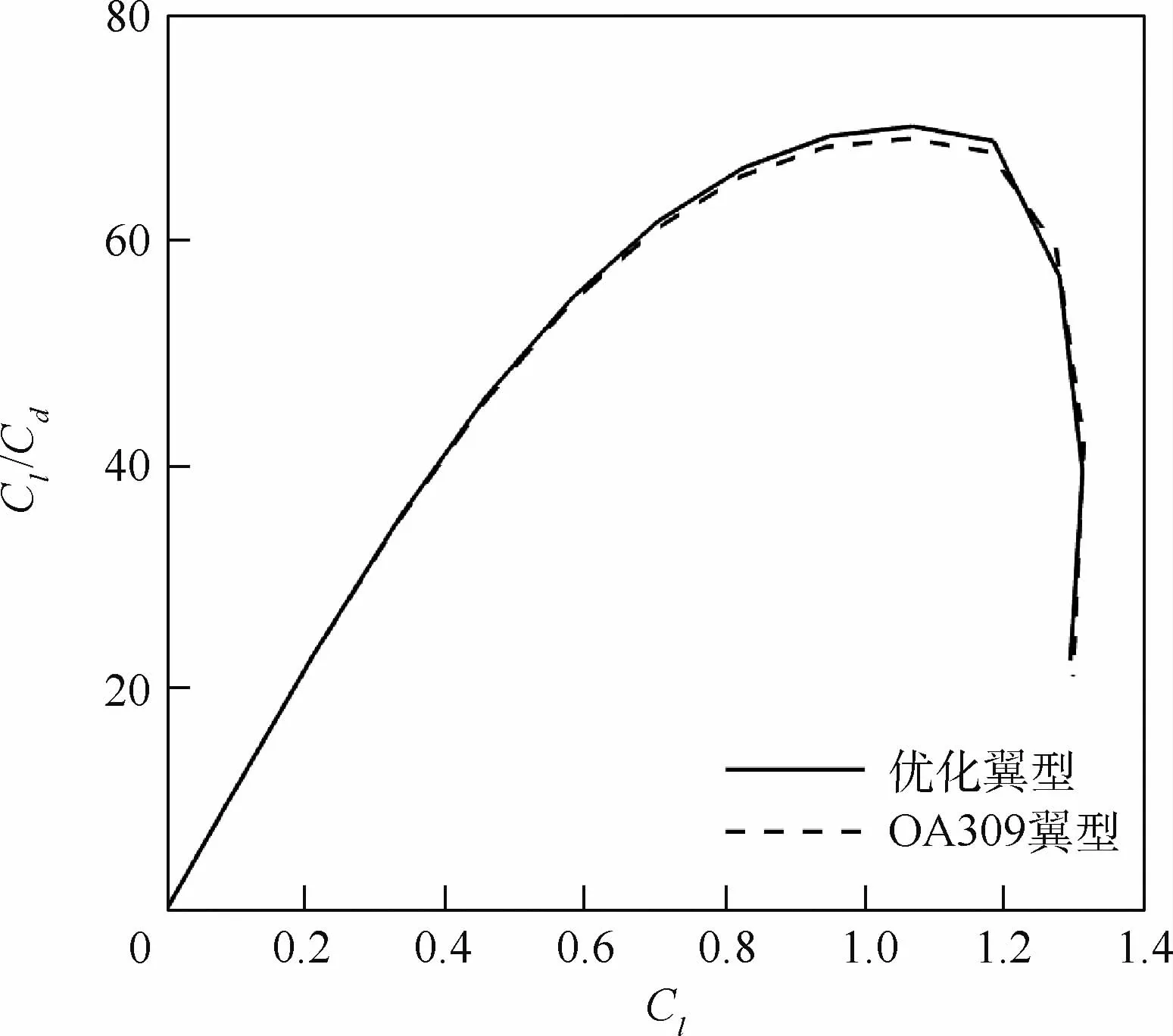
图7 OA309翼型与优化翼型升阻特性对比（Ma=0.4，Re=3.2×106）Fig.7 Comparison of lift drag ratio curves between OA309 and optimized airfoils（Ma=0.4，Re=3.2×106）

图8 OA309翼型与优化翼型力矩特性对比（Ma=0.4，Re=3.2×106）Fig.8 Comparison of moment coefficient curves between OA309 and optimized airfoils（Ma=0.4，Re=3.2×106）

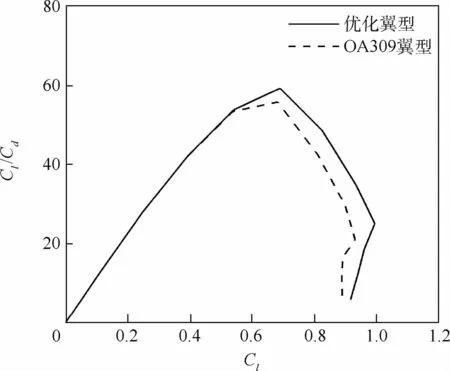
图9 OA309翼型与优化翼型升阻特性对比（Ma=0.6，Re=4.8×106）Fig.9 Comparison of lift drag ratio curves between OA309 and optimized airfoils（Ma=0.6，Re=4.8×106）

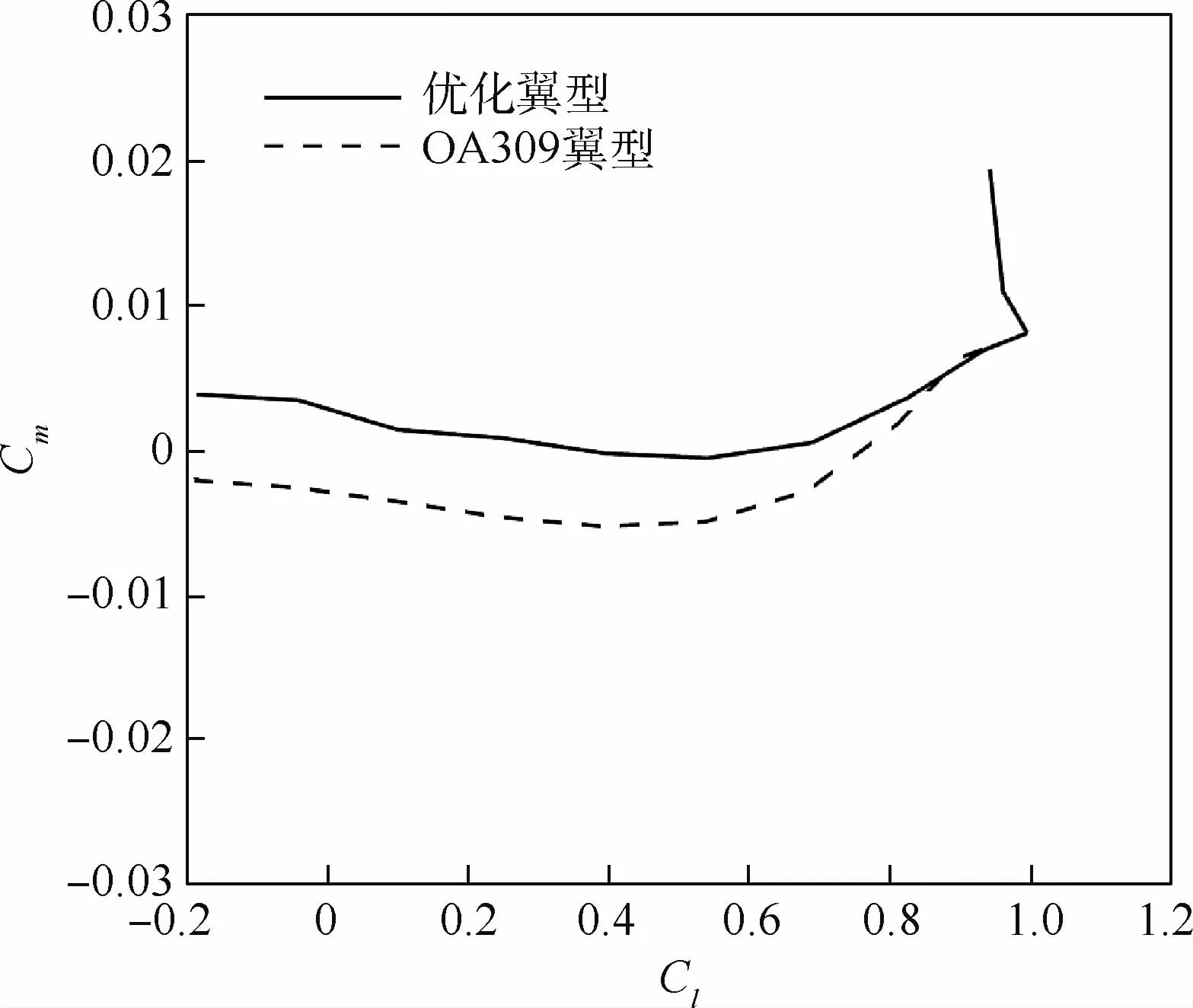
图10 OA309翼型与优化翼型力矩特性对比（Ma=0.6，Re=4.8×106）Fig.10 Comparison of moment coefficient curves between OA309 and optimized airfoil（Ma=0.6，Re=4.8×106）

图11给出了优化翼型与OA309翼型的阻力发散特性。从图中可以看出，在一定速度范围内，优化翼型具有更低的阻力水平，在Ma=0.83之前，阻力系数增长更加缓慢。尽管之后阻力系数增长较快，但翼型很少工作在更高的马赫数下。因此，优化翼型具有更好的阻力发散特性。综上所述，优化翼型保持了低速的高升力特性，提高了高速时的阻力性能，同时提升了力矩特性。

图11 OA309翼型与优化翼型阻力系数随马赫数变化特性对比（Cl=0，Re=Ma×8×106）Fig.11 Comparison of drag coefficient varying with Mach number between OA309 and optimized airfoils（Cl=0，Re=Ma×8×106）

3.2 12%厚度旋翼翼型高维多目标算例

以OA312翼型为初始翼型，进行旋翼内段翼型优化，设计状态如表6所示。设计考虑低速时的最大升力特性、高速时的翼型阻力及阻力发散马赫数。定义设计问题如下：

表6 12%厚度旋翼翼型设计目标与约束Table 6 Design objectives and constraints for a rotor airfoil with 12% thickness

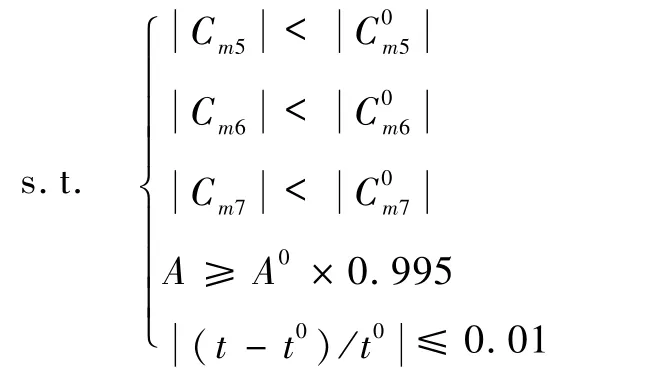
式中：下标数字对应设计状态；设计状态5、6、7对应的马赫数分别为0.74、0.75、0.76；Re=Ma×8×106；其余符号含义同3.1节。

翼型参数化方法、设计变量选取和优化算法参数设置与3.1节相同。采用SOM方法进行优化结果后的处理。SOM 可视化结果如图12所示。从图中明显看出，目标1与目标3、4是相互矛盾的，而目标1与目标5则有较好的正相关关系。OA312翼型具有较高的低速最大升力系数，因此，在确保升力系数不损失的情况下，尽可能降低高速工况阻力。最终，选取的一组解在图12（f）中标记出来，相应的目标值如表7所示。选取表中第2个最优解，利用CFD进行详细性能分析。

图12 最优Pareto前沿SOM可视化结果（12%厚度翼型）Fig.12 Visualization results of optimal Pareto front using SOM（airfoil with 12% thickness）

表7 Pareto前沿中选取的5组最优目标Table 7 Five gr oups of optimal objectives selected from Pareto front

图13为优化翼型与OA312翼型的几何形状对比，表8中为翼型的几何信息，包括最大相对厚度与翼型面积，从表中看出，优化翼型的相对厚度与无量纲面积均满足约束条件。

表8 OA312翼型与优化翼型几何信息Table 8 Geometr y information of OA312 and optimized airfoils

图13 OA312翼型与优化翼型形状Fig.13 Geometry shape of OA312 and optimized airfoils

图14给出了翼型在Ma=0.4时的升阻特性。从图中看出，在升力线性段，两者无明显差别，优化翼型的最大升力系数略有下降。图15给出了Ma=0.4时的翼型力矩特性，优化翼型相比OA312翼型的力矩特性有明显改善。在Ma=0.6时，优化翼型的升阻特性略优于OA312翼型（见图16）。同时力矩特性改善明显，如图17所示，的最大值减小约11%。

图14 OA312翼型与优化翼型升阻比对比（Ma=0.4，Re=3.2×106）Fig.14 Comparison of lift-to-drag ratio curves between OA312 and optimized airfoils（Ma=0.4，Re=3.2×106）

图15 OA312翼型与优化翼型力矩特性对比（Ma=0.4，Re=3.2×106）Fig.15 Comparison of moment coefficient curves between OA312 and optimized airfoils（Ma=0.4，Re=3.2×106）

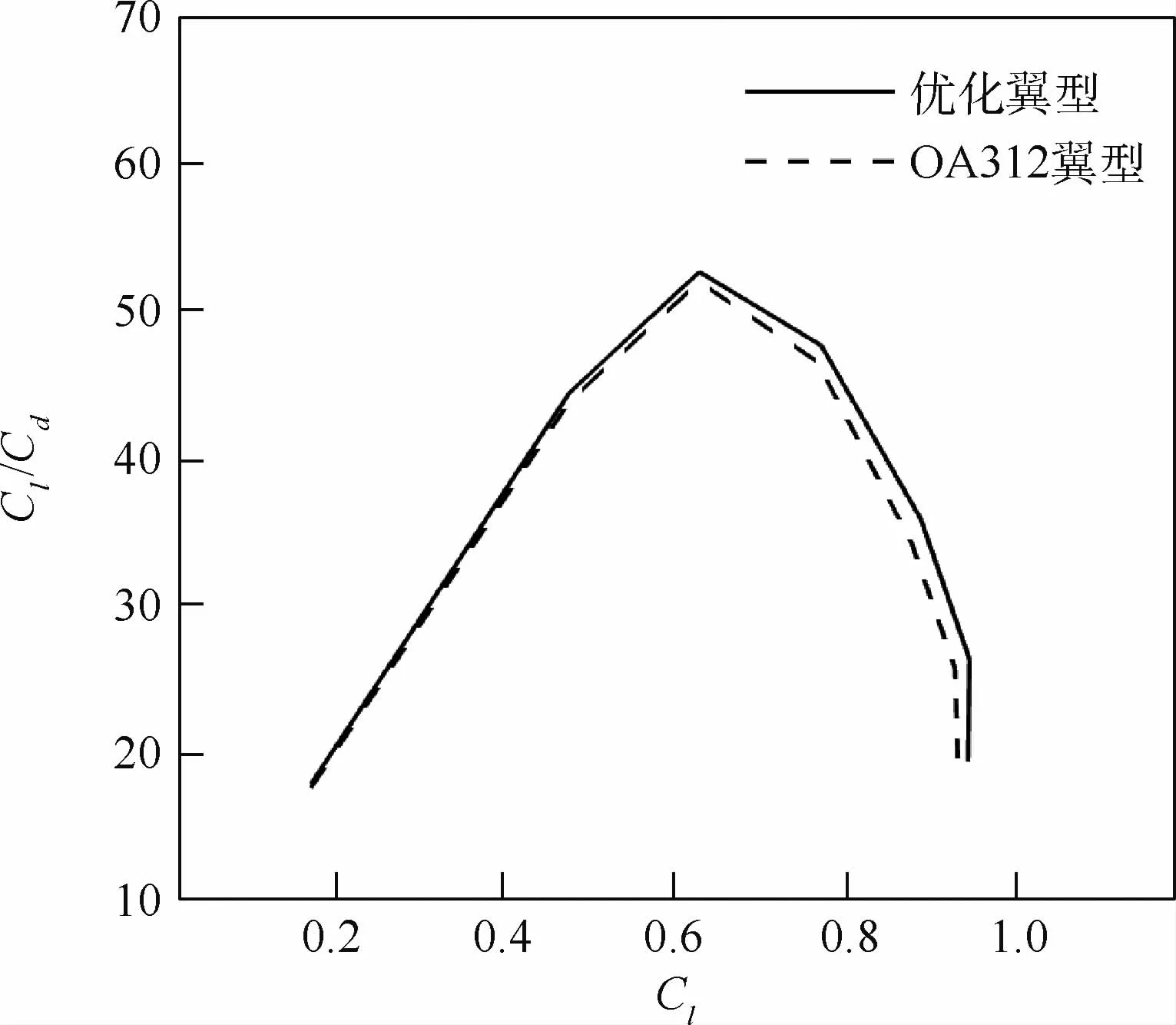
图16 OA312翼型与优化翼型升阻特性对比（Ma=0.6，Re=4.8×106）Fig.16 Comparison of lift-to-drag ratio curves between OA312 and optimized airfoils（Ma=0.6，Re=4.8×106）

图17 OA312翼型与优化翼型力矩特性对比（Ma=0.6，Re=4.8×106）Fig.17 Comparison of moment coefficient curves between OA312 and optimized airfoils（Ma=0.6，Re=4.8×106）

图18给出了优化翼型与OA312翼型的阻力发散特性。从图中可以明显看出，优化翼型在较宽的马赫数范围内保持着更低的阻力系数，其中在Ma=0.76处减阻效果为6.1%。

图18 OA312翼型与优化翼型阻力系数随马赫数变化特性对比（Cl=0，Re=Ma×8×106）Fig.18 Comparison of drag coefficient varying with Mach number between OA312 and optimized airfoils（Cl=0，Re=Ma×8×106）

综上，旋翼内段翼型的优化取得了良好效果，在保持低速高升力特性的同时，明显提高了高速时的阻力性能，同时提升了力矩特性。

4 结论

基于MOEA/D算法，本文提出了旋翼翼型高维多目标优化设计方法，采用kriging代理模型提高了求解效率，并应用SOM方法对最优Pareto解集进行了可视化分析。旋翼翼型5目标优化设计的结果表明：

1）MOEA/D算法能够有效求解高维多目标气动优化设计问题；结合高精度代理模型，能够高效解决旋翼翼型复杂气动优化设计问题。

2）高维多目标优化设计结果难以通过二维图表直观地展示最优Pareto前沿。SOM 聚类分析能够为设计者的决策提供较好的全局可视化结果，有助于从Pareto前沿中选取综合性能良好的设计结果。

3）旋翼翼型高维多目标设计避免了设计目标的加权或折中处理，利用高维多目标进化算法实现了翼型阻力特性、力矩特性和阻力发散特性的综合提升，能够提高旋翼悬停、机动性能和操纵特性。