基于智能优化箱粒子滤波的移动机器人FastSLAM

罗景文，秦世引

（1.云南师范大学 信息学院，昆明 650500；2.北京航空航天大学 自动化科学与电气工程学院，北京 100083）

随着人工智能和机器人技术的高速发展及其在各行各业的推广应用，人们对于拥有自主作业能力的智能机器人的需求日益增加，而同步定位与地图构建（simultaneous localization and mapping，SLAM）是实现机器人真正智能化的关键支撑技术。目前，针对SLAM 的求解途径大致可归纳为基于最优滤波的方法和基于图优化的方法［1］。其中，基于最优滤波的方法主要依据递归贝叶斯状态估计理论，主要包括基于扩展卡尔曼滤波（extended Kalman filter，EKF）的方法和基于粒子滤波（particle filter，PF）的方法。对于在EKF架构下解算的SLAM 算法，环境特征的感知信息会随着机器人的运动持续地加入到联合状态特征向量及其协方差矩阵中，其主要问题在于对特征点深度和协方差矩阵的初始值依赖较大，如果设置欠妥，则会使得估计结果不一致，甚至导致算法 不 收 敛［2-3］。为 此，Doucet等［4］根 据Rao-Blackwellized粒子滤波（Rao-Blackwellized particle filter，RBPF）的分解思想提出了RBPF-SLAM，该方法可以有效解决地图构建过程中的数据关联问题，并且可以根据实际应用需要构建出不同类型的 地 图。随 后，Montemerlo 等［5］又 提 出 了FastSLAM算法，并通过进一步改进和优化提出了更加完善的版本FastSLAM 2.0［6］，但该算法需要采样足够数量的粒子才能正确完成地图构建，由于每个粒子都存储了一张周围环境的完整地图，同时又包含了机器人轨迹估计的结果，需要占用大量的计算资源和存储空间。因此，FastSLAM 类算法面临的主要挑战是如何尽可能减少采样所需的粒子数。为了解决算法存储量过大的问题，Eliazar和Parr［7］研究并提出了一种基于分布式粒子的SLAM算法，大幅度降低了算法占据的存储空间。为了减少地图构建过程中需要采样的粒子数，通常采取将当前时刻的观测与已构建的地图进行扫描匹配，再将匹配结果替代误差较大的里程计读数，进而改善粒子采样的提议分布［8-10］。

然而，这类基于概率的SLAM 算法中都存在一个共同的缺陷，即滤波一致性问题。Bailey等［11］研究发现，RBPF-SLAM 在足够数量粒子条件下可以构建出较为准确的地图，但其滤波结果的一致性仅在较短时间内满足要求。而此问题如果采用区间分析（interval analysis，IA）技术则可以得到有效地解决［12］。这是由于区间分析所针对的运算对象是区间量，当浮点数受到四舍五入运算的影响产生误差时，利用区间运算却能得到包含精确解的严格区间界限，因此可以提供有界的结果，保证了滤波的一致性。Gning等［13］将区间运算的特点与传统PF不受系统模型约束的性能优势相结合，提出了一种新颖的非线性滤波算法，称为箱粒子滤波（box particle filter，BPF），其核心思想是：将传统的点粒子和系统误差统计模型分别取代为区间箱粒子和系统误差界限模型，再进行贝叶斯滤波。相比于传统PF，其最大的性能优势在于所需采样的箱粒子数少且运行速度快，因而算法的运算复杂度低、实时性好。在目标跟踪领域的一些应用中［14-15］，BPF只需采样数十个箱粒子就可以达到与传统PF采样数千粒子所获得的滤波精度和可靠性。

基于以上分析，本文在FastSLAM 算法架构基础上，充分利用BPF所需粒子数少、运行速度快的性能优势，针对BPF中的箱粒子退化现象，综合运用萤火虫算法（firefly algorithm，FA）［16］的寻优机制和IA技术，创立高性能的智能优化BPF算法，使得箱粒子集朝着机器人真实轨迹靠近，进而提高移动机器人位姿估计和同步定位的精度。结合扩展区间卡尔曼滤波（extended interval Kalman filter，EIKF）［17］完成环境地图的构建和更新，进而增加路标协方差矩阵预测和更新的精度和鲁棒性。

1 区间分析

在区间分析［18］中，一维闭合区间定义了实数域中一个连续、封闭的子集：

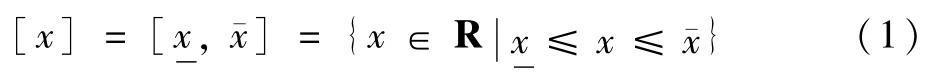
如果将上述区间的定义推广至Rn维实数空间，则n维区间向量，或称n维箱粒子［X］定义了n个一维闭合区间的笛卡儿积。

图1展示了一个二维实数域中的箱粒子，其基本数学定义如表1所示。

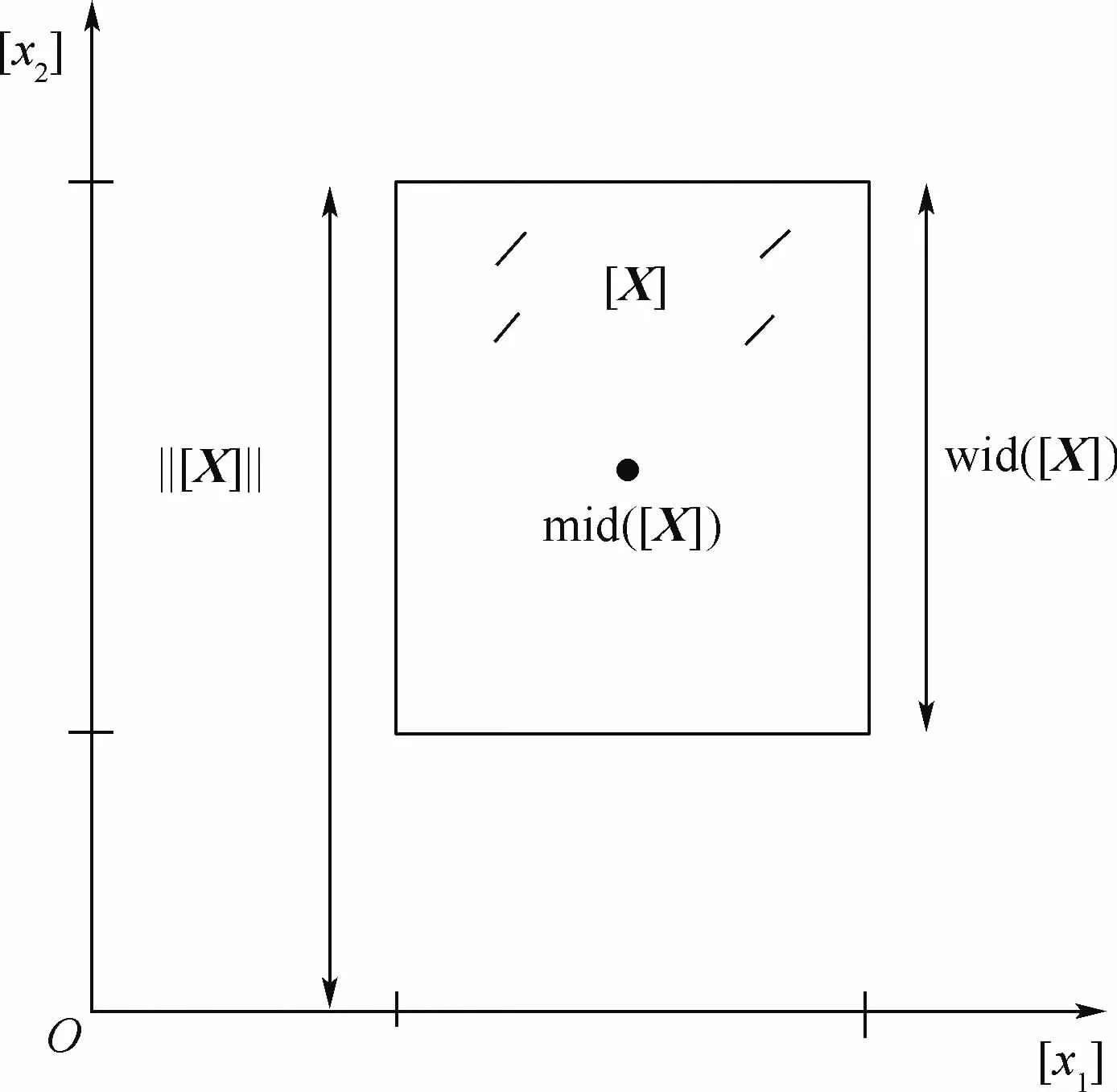
图1 二维空间中的箱粒子及其数学定义Fig.1 Box particle and its mathematical definition in two-dimensional space

表1 二维箱粒子的基本数学定义Table 1 Basic mathematical definition of two-dimensional box particle

一般情况下，Rn空间中的箱粒子［X］经过非线性函数f映射后所得到的f（［X］）为非规则的箱体形状。为了便于计算和分析，使得［X］在非线性函数的映射作用后得到规则的箱体形状，区间分析定义了包含函数（inclusion functions），即已知函数f：Rn→Rm，则其对应的区间函数［f］：IRn→IRm是包含函数，如果满足：

式中：IRn为n维实区间的集合。

对于各种类型的函数f，区间分析的一个主要目的就是提供合理有效的包含函数［f］，使得［f］（［X］）在包含所有可能解的同时其区间所含范围不太大，这样就可以很大程度上减少算法的计算量，提高收敛速度。为此，区间分析引入了区间约束（interval constraint）的概念，即利用某种特定算法对原区间进行约束，也就是解决约束满足问题（constraint satisfaction problem，CSP），其定义为：在n维实数域上，实值约束函数g（x）=g（x1，…，xn）=0的约束集为

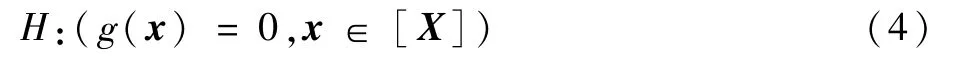
式中：g（x）=（g1（x），g2（x），…，gm（x））T，x=（x1，x2，…，xn）。则CSP的解集为

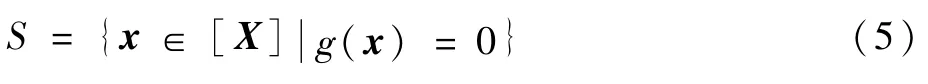
在式（4）中，H的本质就是求解出一个包含［X］中所有x，并满足约束函数g（x）的具有最小冗余的箱粒子［X］′，进而利用［X］′代替［X］，即S⊆［X］′⊆［X］。在BPF中，箱粒子的区间收缩一般采用前向后向传播算法，也称约束传播（constraints propagation，CP）算法或CP收缩子，该算法的特点是实现起来简单，而且在高冗余数据和约束情况下，具有较高的执行效率［13］。

2 智能优化箱粒子滤波

2.1 箱粒子滤波算法

BPF充分结合了序列蒙特卡罗（sequential Monte Carlo，SMC）方法和IA技术，其核心思想是：利用在状态空间中随机采样的具有一定体积的箱粒子代替常规的点粒子，再利用系统误差界限模型代替系统误差统计模型对加权箱粒子集进行序贯迭代。在区间分析的框架中，k时刻系统状态向量xk和观测向量zk分别表示为区间状态向量［Xk］∈IRnx和区间观测向量［Zk］∈IRny。同理，状态转移函数f和观测函数h分别表示为包含函数［f］和［h］，则系统状态方程为

式中：［Vk］和［Wk+1］分别为状态转移噪声和观测噪声箱粒子；［Uk］为控制输入箱粒子。

Gning等［19］在贝叶斯滤波框架下将BPF视为采用混合均匀概率密度函数（probability density function，PDF）的滤波算法，即将每个箱粒子内部都拟合为一个以该箱粒子为支撑集的均匀PDF，每个PDF很好地描述了对应箱粒子的状态特性。因此，若令U［X］表示以箱粒子［X］为支撑集的PDF，则随机变量x可表示为一组均匀PDF的加权和。

式中：N为混合均匀PDF的数目；［Xi］为第i个箱粒子；=1，∀i，ωi≥0。

基于上述分析，根据贝叶斯滤波估计原理，BPF的迭代步骤如下：

1）预测。在k时刻，假设状态xk的PDF可表示为

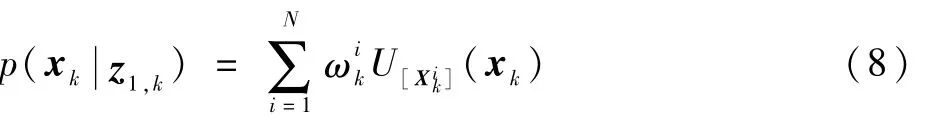
则时间更新步骤如下：

3）重采样。针对BPF中的箱粒子退化现象，通常采取计算有效样本Neff=的大小，并选择一个阈值Nth，如果Neff＜Nth，则执行随机子划分重采样，即根据需要重采样的次数，将当前时刻得到的箱粒子随机地选取其某一维状态子区间进行均匀的划分，使得箱粒子能够保持一个合适的尺寸。该方法不但保证了当前时刻的箱粒子集能够顺利进入下一时刻的迭代，而且也有效去除了箱粒子内部的冗余区域。然而，该方法对箱粒子的子区间进行选取是随机的，这会导致每次实验的结果都不同，因此反复执行随机子划分重采样对滤波精度影响较大。

2.2 萤火虫算法智能优化箱粒子滤波

尽管BPF在许多实际的应用中被证明是有效的，但对于高非线性系统和观测误差较大的情况下，其滤波精度不高［20］。作为一种新的非线性滤波算法，BPF的发展时间较短，理论体系还需进一步完善，算法的性能还有进一步提高的空间，其应用方面则主要集中在目标跟踪领域。针对箱粒子的退化现象，考虑结合FA的寻优机制对箱粒子集的空间分布进行智能优化，以改善BPF的滤波性能。

FA［16］是受自然界中的萤火虫通过荧光进行信息交流的群体行为启发而演变得来的。萤火虫的荧光亮度和萤火虫间的吸引度是FA的2个主要因素。其中，荧光亮度用于表示萤火虫所处当前位置的优劣程度，并决定了其下一时刻的运动方向；吸引度表示萤火虫之间的相互作用，并决定了萤火虫移动的距离。FA就是通过对荧光亮度和吸引度的不断迭代，使得萤火虫群体智能地向状态空间内更好的区域运动，进而实现目标的优化。

FA作为一种新型仿生群智能优化算法，其最大的优势在于在工程上容易实现，需要调整的参数少，具有较好的收敛速度和收敛精度。文献［21］将FA的优化机制应用于PF，提高了PF的估计精度，降低了状态估计所需的粒子数。因此，本文考虑结合BPF的运行机制和FA的寻优机制，根据最新观测利用区间分析定义箱粒子的荧光亮度计算公式及空间位置更新公式，进而模拟萤火虫进行觅食或交流的个体行为，使得箱粒子智能地向全局范围内更优的位置移动，这样就可以提高箱粒子集的整体质量，克服箱粒子的退化问题，避免了反复执行随机子划分重采样。

1）箱粒子的荧光亮度更新公式。在标准FA中，当前时刻的每个萤火虫都需要和其他位置的萤火虫对比荧光亮度值大小，萤光亮度值低的萤火虫会被萤光亮度值高的萤火虫吸引，并朝着萤光亮度值高的萤火虫所处的空间位置移动。因此，萤火虫的相对荧光亮度更新公式定义为

式中：Im和γ分别为萤火虫的最大萤光亮度和光强吸收系数；dij为萤火虫i与j的空间欧氏距离。

如果直接将式（20）的更新机制应用于BPF，则将会进一步增加算法的运算复杂度。为了确保滤波精度，萤火虫在自适应迭代寻优过程中需要考虑最新的观测。而在区间分析的框架下，其关键思想就是求出当前时刻的预测观测和实际观测在多维状态空间中的“交”。因此，构造箱粒子荧光亮度的计算公式为

根据式（21），由于每个时刻的实际观测值仅有一个，利用实际观测值和每个箱粒子的预测观测值进行对比，代替每个箱粒子之间荧光亮度值的对比，就可有效减小算法的运算复杂度。

2）箱粒子的吸引度计算公式。在标准FA中，萤火虫的吸引度公式为

式中：βm为最大吸引度，一般设置为［0.8，1］内的常数。

如果萤火虫的吸引度越大，则其越容易吸引附近的萤火虫向自身所处的位置运动，这样一来，就会使得所有箱粒子都集中在状态的真实值附近，造成箱粒子的多样性丧失。基于上述分析，根据区间分析中2个中心区间距离的定义，给出k+1时刻箱粒子与全局最优箱粒子［gk+1］之间的空间欧氏距离为

式中：·2为2-范数。

在箱粒子荧光亮度更新公式基础上，进一步考虑在吸引度公式中加入一个随机权值项，这样就能改变箱粒子的移动信息，既能让箱粒子集在高似然区域合理的分布，又可以在一定程度上增强箱粒子的多样性，确保了滤波过程的持续运行。因此，构造箱粒子间的吸引度为

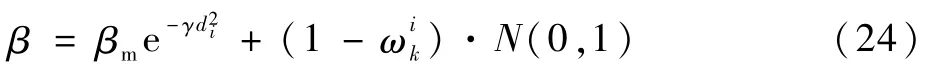
式中：N（0，1）为均值为0、方差为1的高斯分布随机向量；（1-）·N（0，1）为随机权值项。

当完成位置更新之后，需要计算并对比箱粒子的荧光亮度值，更新全局最优箱粒子：

3）箱粒子的位置更新公式。在标准FA中，萤火虫i被萤火虫j吸引后移动的位置更新公式为

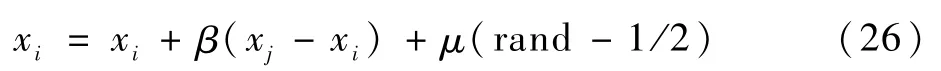
式中：xi和xj分别为萤火虫i和j的空间位置；rand表示某个随机数，且服从均匀分布U（0，1）；μ∈［0，1］为步长因子。

如果将式（26）的更新策略直接应用于BPF，则需要用箱粒子i和其余的箱粒子j进行交互运算，这将对算法的实时性带来不利影响。为此，考虑利用每个箱粒子与全局最优箱粒子间的对比来替代箱粒子间的相互对比，利用每个箱粒子中心位置的更新使每个箱粒子的位置更新，这会提高FA的全局寻优能力，且该阶段的运算复杂度将由O（N2）减少至O（N）。基于上述分析，构造箱粒子的位置更新公式为

由式（27）可知，箱粒子的随机步长随di变化，且2di（rand-1/2）∈［-di，di］。采用上述位置更新策略后，当箱粒子间的空间位置相距较远时，箱粒子位置更新过程中吸引度所发挥的引导作用相对较弱，而箱粒子自身可以在区间［-di，di］内随机自主的运动，这样就使得算法能够搜索较大的状态空间；当箱粒子之间的空间欧氏距离较近时，箱粒子在状态空间中的自主探索能力和移动范围随着空间欧氏距离di的减小而减弱，而此时箱粒子在位置更新过程中，吸引度起到的主导作用将逐渐增大，进而智能地引导箱粒子朝着全局最优的箱粒子所在位置移动。

通过以上优化策略，利用FA智能优化引导箱粒子集朝着高似然区域移动，可以有效克服箱粒子的退化现象，并且没有增加额外的操作和参数，保持了算法的简单性。另外，考虑到FA本身具有较强的收敛能力，如果迭代次数过多，则会造成算法的计算复杂度增高，而且利用FA智能优化的目的是为了使得箱粒子集朝着似然度高的区域移动，不需要收敛到最优值，否则会造成箱粒子的多样性丧失。因此，通过设定最大迭代次数，保证算法的实时性和箱粒子多样性，即当荧光亮度函数值大于设置的迭代终止阈值时，算法停止迭代，否则继续执行迭代，直至到达最大迭代次数。当算法迭代至设定阈值时，表明箱粒子已经较好地分布在状态的真实值周围。

3 移动机器人FastSLAM 方案设计

FastSLAM 算法的核心在于运用RBPF思想对SLAM问题后验概率进行分解，其实现了地图规模和状态估计之间的有效解耦。具体说来，就是将SLAM问题分解成为机器人路径x1：k估计和基于该路径估计的地图M 创建2个子问题，即

式中：z1：k=｛z1，z2，…，zk｝和u1：k=｛u1，u2，…，uk｝分别为观测序列和控制输入序列；mi为第i个环境路标的位置估计；n1：k=｛n1，n2，…，nk｝为数据关联的相关一致性。

根据SLAM 的动态贝叶斯图模型，当已知机器人的运动轨迹x1：k时，对其周围环境地图M 中存在的N个特征进行估计是相互独立的。因此，FastSLAM采用PF估算机器人所有可能的轨迹后验，其中的每个粒子都包含一份机器人完整的潜在地图。然而，为了提高估计精度，就需要增加描述后验概率分布所需的粒子数，这对于FastSLAM算法来说代价巨大，会增加算法的复杂度。此外，反复的重采样会造成粒子有效性和多样性的损失，导致出现粒子退化现象，使得算法的性能下降，甚至失效；另一方面，在所得路径估计基础上，利用常规EKF对地图特征估计存在计算量过大、精度不高甚至发散等问题。

因此，考虑将改进的智能优化箱粒子滤波（IOBPF）用于实现移动机器人位姿估计，并在此基础上利用EIKF完成地图构建与更新，为了表示方便，简记为IOBPF-SLAM 算法。其中，k时刻第i个箱粒子的结构形式如下：

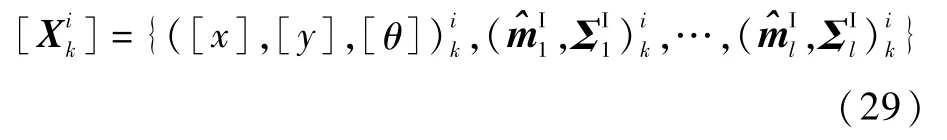
3.1 移动机器人同步定位

在区间分析框架下，移动机器人系统的运动模型表示为

式中：k时刻的输入区间向量［Uk］由机器人的基本位移［Δdk］和基本旋转角［Δθk］组成，即［Uk］=（［Δdk］，［Δθk］）T，（［x］×［y］）T为机器人在全局坐标系下的位置，［θ］为机器人运动方向。

机器人系统的距离-角度观测模型为

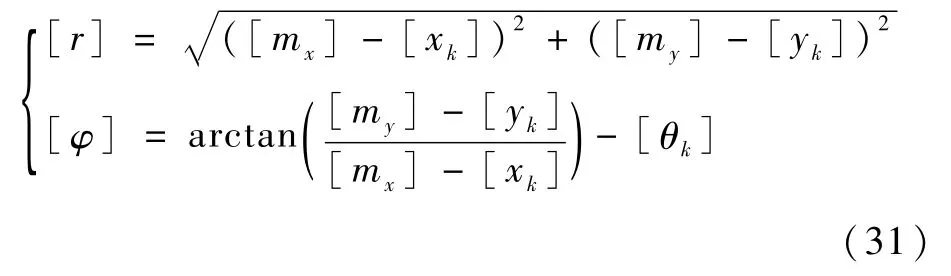
式中：观测区间向量［Zk］由距离观测区间量［rk］和角度观测区间量［φk］组成，即［Zk］=（［rk］，［φk］）T。

因此，k+1时刻的状态估计值为

在具体应用中，可将权值最大的箱粒子的中心近似为状态估计值。另外，针对估计值，其对应的状态估计协方差为

3.2 环境地图构建

Chen等［17］将区间分析引入卡尔曼滤波，将噪声模型和系统模型的误差用区间范围来表示，提出了一种新的区间卡尔曼滤波（interval Kalman filter，IKF）算法，其迭代公式与标准卡尔曼滤波的结构形式完全相同，只是运算变量为区间向量或区间矩阵，估计结果为2条边界曲线，最终结果将2个边界值取平均或加权处理获得。由于区间运算保证了结果的完备性，在一些实际应用中［22-23］，IKF相比于卡尔曼滤波展示出了更好的鲁棒性和精度。

对于区间非线性系统，结合IKF和EKF便可进一步得到EIKF的迭代公式。为了下文表示方便，利用上标“I”表示区间量，即［Xk］表示为，状态转移包含函数［f］和观测包含函数［h］分别表示为fI和hI，为状态估计的区间协方差矩阵，和分别为系统噪声区间协方差矩阵和观测噪声区间协方差矩阵，则EIKF算法的递归过程如下。

1）状态初始值。

2）计算区间雅可比矩阵。

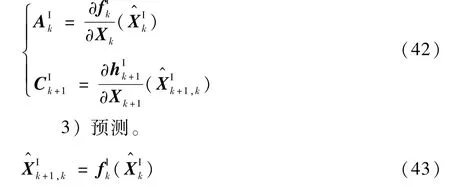
4）计算新息和区间卡尔曼增益。

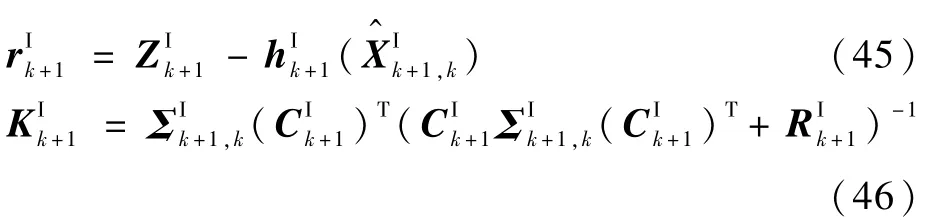
5）更新。

常规FastSLAM 算法利用EKF更新地图，但需要对非线性的模型进行线性化。由于机器人系统具有强非线性，线性化只能精确到泰勒级数的一阶，造成估计精度下降甚至导致滤波发散。因此，本文利用EIKF取代EKF完成环境特征估计。根据FastSLAM 的解算过程，如果机器人的运动轨迹已知，则对各个特征进行估计彼此是相互独立的，而k+1时刻是否对第j个环境特征进行更新取决于k时刻第j个特征是否被传感器观测到。从而，根据传感器获得的最新观测完成数据关联后，需考虑以下情况：

3）如果机器人最新的观测没有包含环境地图中的第j个路标，则其均值和协方差不变。

4）如果机器人再也没有观测到周围环境的任何特征，则将前一时刻的地图信息作为当前时刻的地图信息。

在上述EIKF的递推式中，增益矩阵的计算涉及区间矩阵的求逆，而这类求逆问题往往采用迭代的方式求解，算法比较复杂，且耗时长，不利于实时性。因此，为了减少计算量，进一步提高算法的实时性，本文采用结合Hansen算法［25］和上边界矩阵的区间矩阵求逆方法，具体见算法1。

算法1区间矩阵的求逆算法。

综合上述，IOBPF-SLAM 算法的整体结构如图2所示。

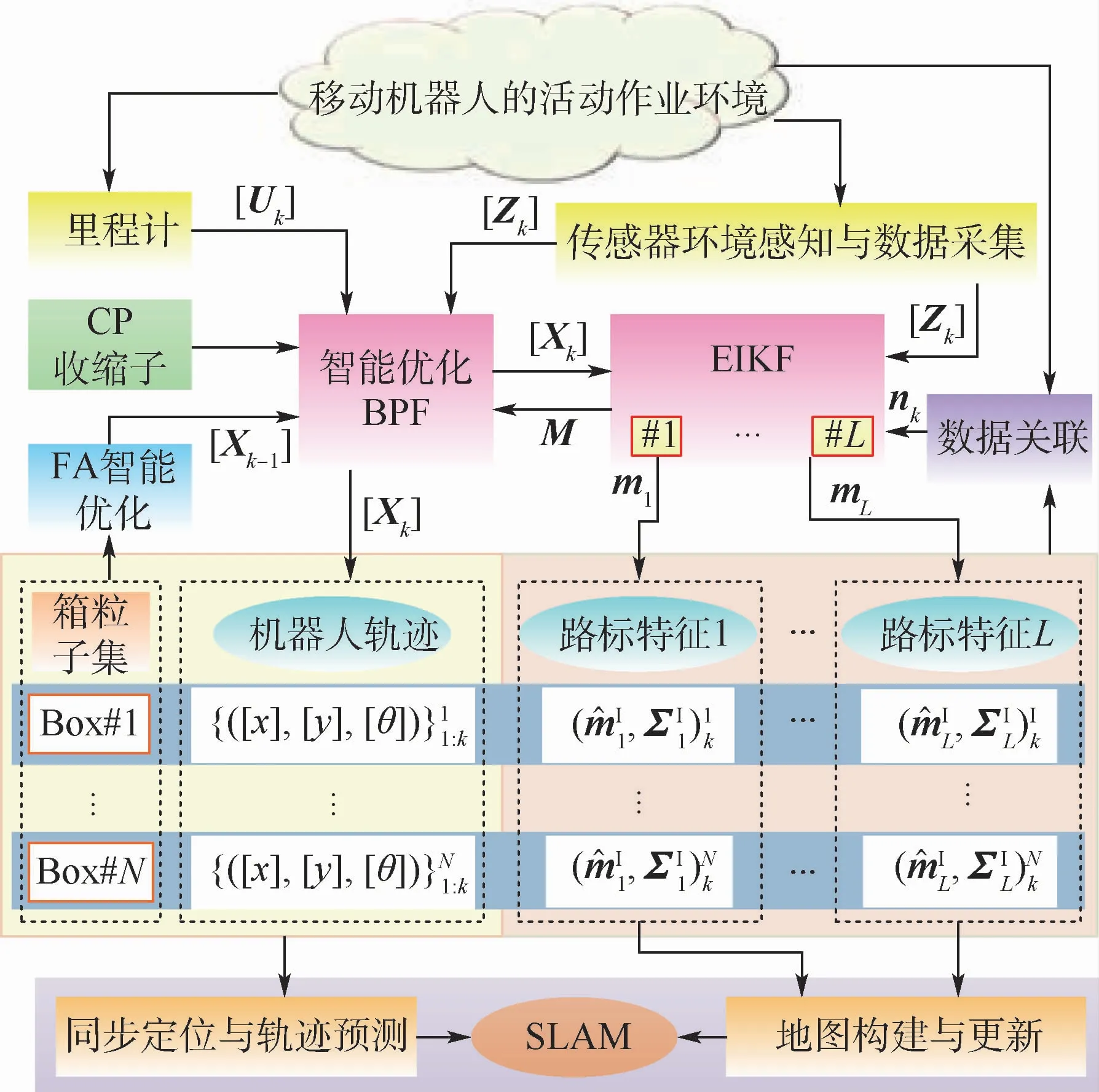
图2 IOBPF-SLAM算法的整体结构Fig.2 Overall structure of IOBPF-SLAM algorithm

4 仿真实验与结果分析

4.1 仿真实验对比分析

为了验证本文算法的性能，根据Bailey［26］开发的SLAM算法通用模拟器设计了尺寸为180 m×80 m，并具有60个路标特征的环境地图及机器人运行参考 轨 迹，分 别 对 FastSLAM 2.0、UFastSLAM［27］、STSRCDKF-SLAM［28］、基于标准BPF算法的BPFSLAM及IOBPF-SLAM开展一系列仿真实验并对相关性能进行对比分析。仿真实验在MATLAB 2014a环境下运行，区间运算利用INTLAB 9.0工具箱。计算机的配置型号为：CPU Intel® CoreTMi5-5200U，主频2.20 GHz，内存8 GB。

仿真中，Np和Nb分别表示粒子数和箱粒子数。对于FA群智能优化步骤，光强吸收系数γ=1，最大吸引度βm=0.85，迭代终止阈值设置为0.02。采用独立兼容最近邻（individual compatibility nearest neighbor，ICNN）算法完成地图构建过程中的数据关联。机器人的初始位置设定为全局坐标系的（0，0）点，并以1.5 m/s的速度运行，其余仿真参数设置如表2所示。根据区间观测的不确定性，传感器观测表示为

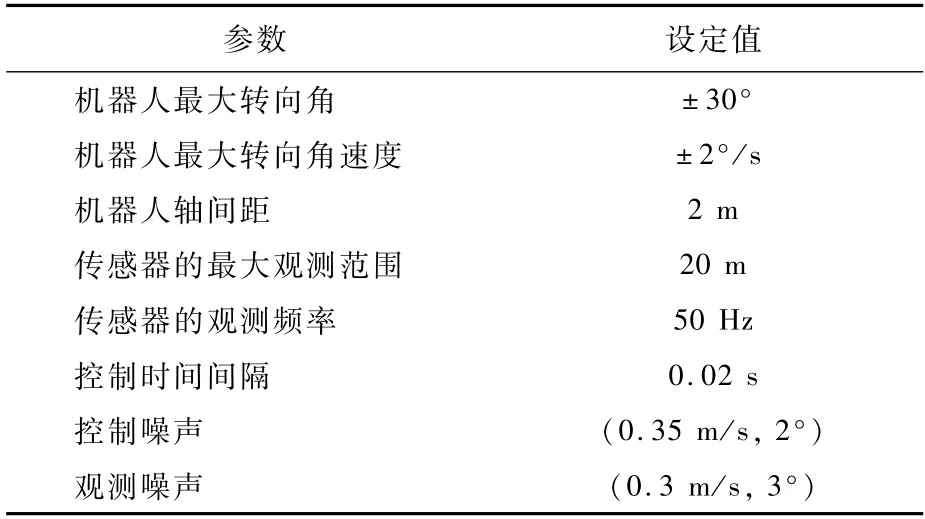
表2 仿真参数设置Table 2 Simulation parameter setting

式中：区间长度Δ=［2.5，2.5］T。

图3展示了5种SLAM算法在模拟环境中的估计结果。可以看出，UFastSLAM 利用无迹粒子滤波（unscented particle filter，UPF）计算机器人状态的不确定性，获得了更加精确的方差，从而改善了估计精度。但随着机器人的持续运动，新的环境特征将不断加入状态向量中，由此引起尺度无迹变换（scaled unscented transformation，SUT）的维数逐渐增加，导致机器人在运动一段距离后，其轨迹估计便开始出现了明显的误差。而STSRCDKF-SLAM利用强跟踪平方根容积卡尔曼滤波，一方面融合了平方根策略，使得其协方差矩阵具备对称性，有效减小了由于系统发生突变导致滤波发散而带来的误差；另一方面，在滤波增益矩阵中加入渐消因子对其进行实时调整，动态自适应地调节数据的权值，进而改善了滤波精度。BPF-SLAM 由于采用IA技术，相比于FastSLAM 2.0在一定程度上提高了估计精度，但由于常规BPF面对箱粒子退化现象需要执行反复地进行随机子划分重采样，也出现了一定的误差，而IOBPF-SLAM估计路径与参考轨迹吻合度更高，相对应的路标估计也更为准确。

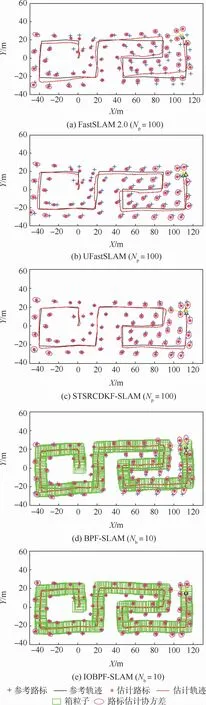
图3 模拟环境下的不同SLAM算法运行结果比较Fig.3 Comparison of running results among different SLAM algorithms in simulation environment

为了验证算法在增长观测噪声条件下的误差性能，设置环境特征的角度观测噪声为2°，距离观测噪声分别为0.1，0.3，0.4，0.55，0.7，0.8，1.0，1.2，1.35，1.5 m进行仿真实验。图4展示了上述5种SLAM 算法在开展了30次仿真实验后的均方根误差（RMSE）均值及标准差的比较情况。可以看出，5种SLAM 算法的轨迹估计误差及标准差随着观测噪声的增长逐渐增加。然而，IOBPF-SLAM算法由于采用FA智能优化，提高了箱粒子集的整体估计效能，并提供了全局一致的结果，因此其RMSE均值和标准差增长速度要低于其他算法。这意味着IOBPF-SLAM 的估计精度相较于其他几种算法更好，并具有较好的运行稳定性。

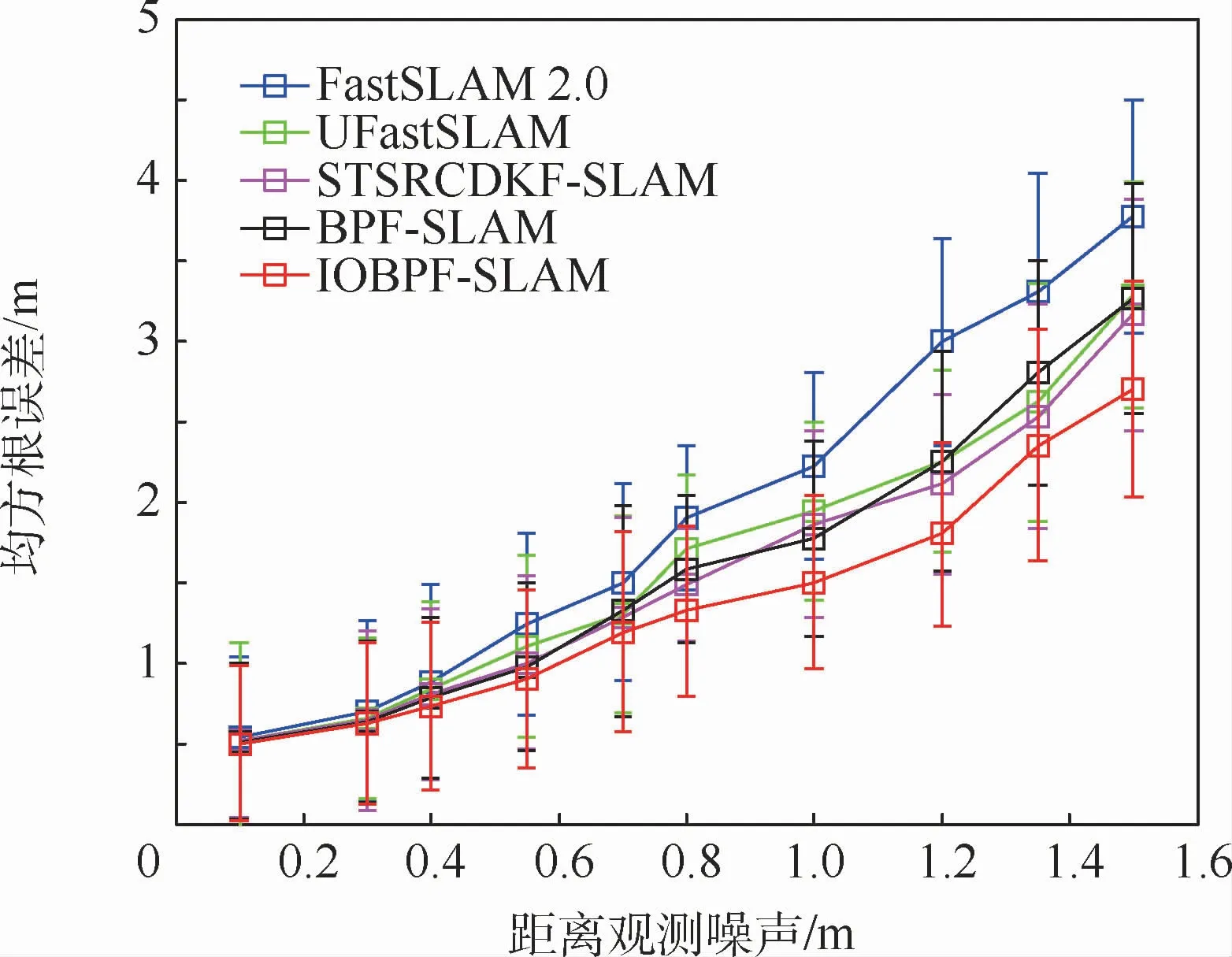
图4 不同SLAM算法的RMSE比较Fig.4 Comparison of RMSE among different SLAM algorithms

为了在上述增长观测噪声条件下验证IOBPF-SLAM能有效避免粒子退化，对于N次仿真实验，利用有效粒子百分比进行评估。

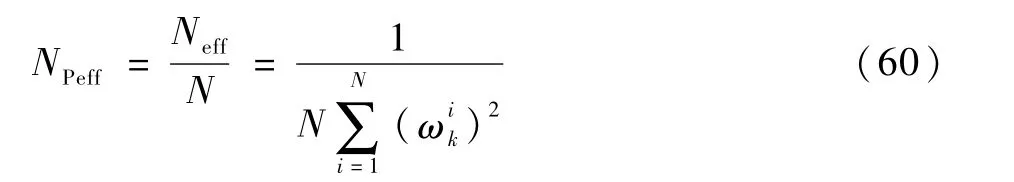
在开展了30次仿真实验后，从图5可以看出，IOBPF-SLAM的有效箱粒子百分比均高于82%，这意味着在算法执行过程中，最多仅有18%的箱粒子没有发挥作用，然而这部分箱粒子主要是为了保持箱粒子的多样性，这说明了FA智能优化的有效性。

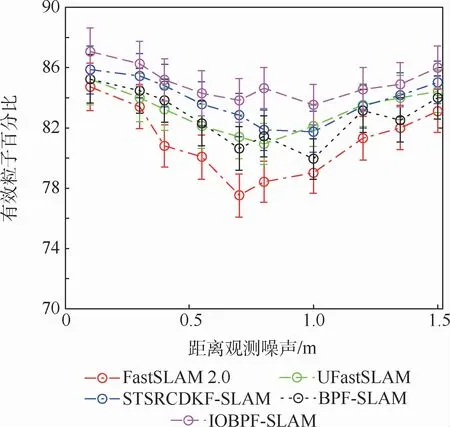
图5 不同SLAM算法的有效粒子数百分比Fig.5 Percentage of effective particle number for different SLAM algorithms

Gning等［19］指出，如果BPF的滤波结果为状态的最优估计，则需要满足：①真实状态向量x必须包含于后验PDF的所有支撑集区域内；②状态后验PDF的支撑集区域体积应该为最小。针对条件①，Gning等［15］进一步指出了包含准则ρk，并说明了当不满足此条件时，该滤波器不收敛。为了解释ρk，需要利用置信集的概念。在BPF中，一般采用所有支撑集箱粒子的“并集”来表示置信集Ck（1），即

因此，包含准则ρk可由如下计算得到：

如果满足ρk=1，则表明在所有以［］为支撑集的后验PDF内已经包含了状态的真实值。从图6可以看出，相比于标准的BPF，IOBPF运用FA优化机制引导箱粒子集智能地向高似然区域移动，使该箱粒子集更好地满足了ρk=1，因此提高了滤波性能。

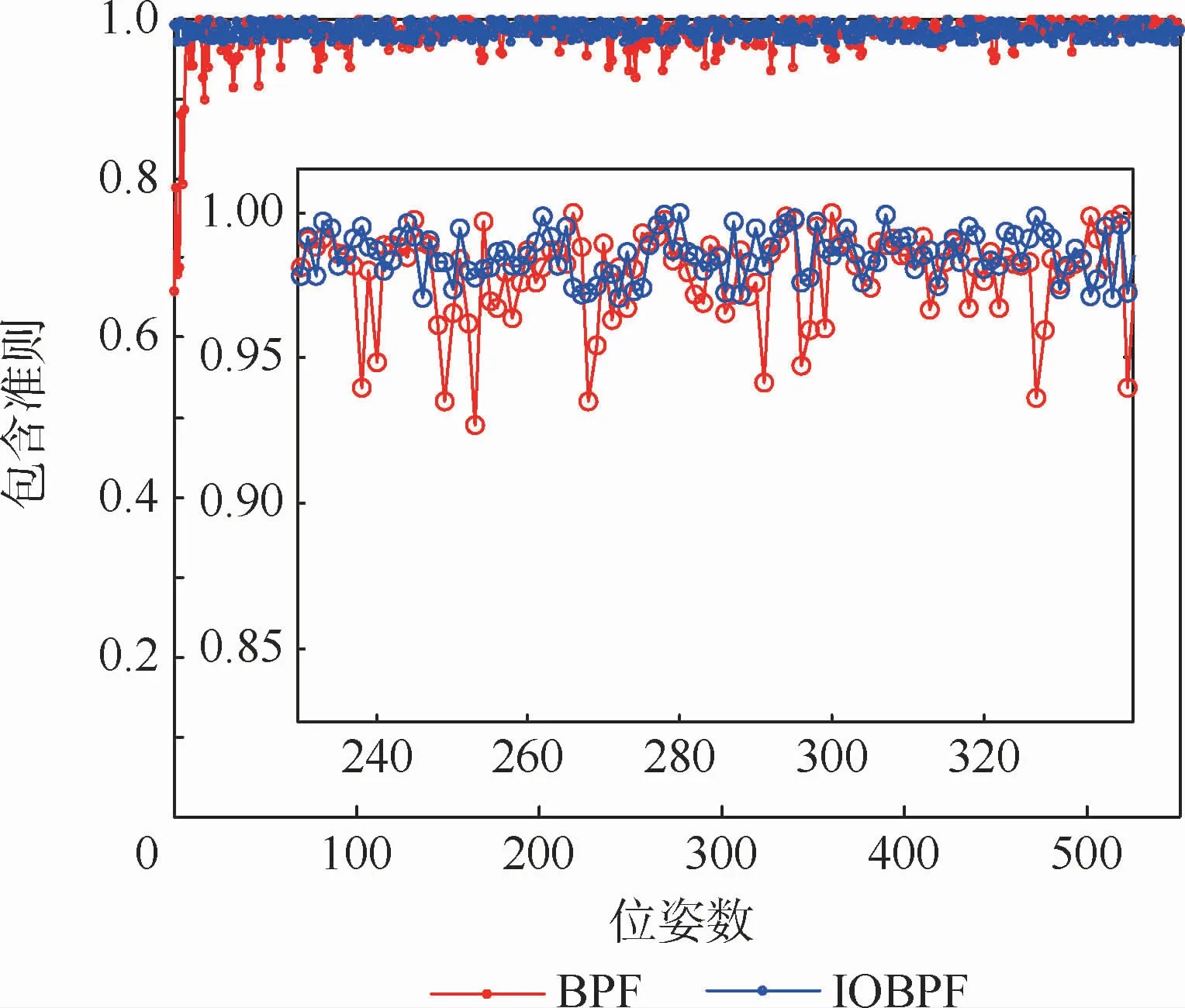
图6 不同箱粒子的包含值Fig.6 Inclusion values of different box particles

对于一个滤波算法而言，如果其估计误差满足：①均值等于零；②小于或等于其计算所得的协方差，则称该滤波算法是一致的。如果一个滤波算法不一致，则其滤波精度就具有不确定性，这会导致算法估计结果不可靠。Bailey等［11］分析并阐述了粒子退化现象是造成FastSLAM 算法不一致的主要原因，并进一步提出了利用归一化估计方差（normalized estimation error squared，NEES）准则来验证算法是否满足一致性。具体而言，假设为k时刻机器人的真实状态，且该状态的维数为d，并假设为其估计值和方差，则NEES计算如下：

NEES本质上描述的是一种加权距离，一般需要开展N 次蒙特卡罗实验，然后采用平均NEES进行检验，即

式中：给定显著性水平α=0.05，并将双边概率为95%的区域作为一致性区域时的界定区间为［2.19，3.93］。

因此，为了评估上述5种SLAM 算法的一致性，分别开展30次仿真实验，结果如图7所示，其中红色的实线和红色的虚线分别表示一致性测试的下限和上限。可以看出，UFastSLAM 采用无迹变换，避免了由于线性化带来的误差，其一致性优于FastSLAM 2.0；而STSRCDKF-SLAM 改进了提议分布，并采用自适应重采样有效保持了粒子的多样性，因此其一致性保持更为持久。相比起来，IOBPF-SLAM在区间分析基础上结合FA的寻优机制，构造了箱粒子集的智能优化策略，因此提供了有界的、更为一致性的结果。

图7 不同SLAM算法的一致性比较Fig.7 Comparison of consistency among different SLAM algorithms

通过对不同SLAM 算法的计算机CPU 运行时间来对比不同粒子数条件下的SLAM算法计算复杂度。对于每组设定的粒子数，分别开展30次仿真实验，其平均计算复杂度如图8所示。可以看出，上述5种SLAM 算法的时间复杂度随着粒子数的增长逐步增加，FastSLAM 2.0的运算复杂度与粒子数呈近似线性关系。在使用相同粒子数的条件下，由于涉及区间运算和群智能优化过程，提出算法的复杂度要高于其他算法，但由上述图3的运行结果可知，IOBPF-SLAM 利用10个箱粒子所获得的估计精度就已经超过前3种基于PF的SLAM 算法。因此，为获得较高的估计精度，IOBPF-SLAM的计算代价相对最低，算法执行所需时间更短。

4.2 移动机器人测试结果与性能评价

为测试IOBPF-SLAM 的实际应用效果，利用装备Raspberrypi-3b控制主板和SLAMTEC激光雷达的差分驱动轮式移动机器人（RPLIDAR-A1）分别针对Grid SLAM［8］、GMapping［9］、BPF-SLAM和IOBPF-SLAM开展对比实验。实验利用一台上位机笔记本电脑在Ubuntu14.04下安装机器人操作系统（ROS），利用teleop_twist_keyboard软件包控制机器人运动，并结合占用概率地图构建方法［29］，采用栅格地图来建立环境模型，通过加载图形可视化工具Rviz显示地图的构建过程。实验场景如图9所示。

图9 差分驱动轮式移动机器人及其实验场景Fig.9 Differential drive wheeled mobile robot and experimental scene

实验中，移动机器人运动速度为0.4 m/s，最大转向速度为0.3 rad/s，控制频率为40 Hz，激光雷达最大测距范围为6 m，并具有360°全方位扫描能力。环境中设置了30个路标点及2个纸箱作为障碍物，生成栅格地图分辨率为25 cm2/cell，粒子数目设置为Np=10，Nb=10。由图10的地图构建过程可以看出，当采用10个粒子时，Grid-SLAM无法正常完成地图构建，而其余3种算法均能完成二维栅格地图构建。

图10 地图构建过程Fig.10 Map building process

为了定量分析实验结果，表3比较了在正确构建出环境地图条件下4种算法的性能参数。可以看出，Grid SLAM需要100个粒子才能正确完成地图构建，而GMapping在RBPF的基础上改进了采样提议分布并采用选择性重采样策略，有效减少了所需粒子数，同时防止了粒子退化现象，是目前最有效的栅格地图构建方法，但仍然需要30个粒子才能完成地图构建。相比起来，BPF-SLAM和IOBPF-SLAM使用更少的粒子数就能完成地图构建，从而提高了SLAM系统的实时性。

表3 不同SLAM 算法的性能比较Table 3 Comparison of per formance among different SLAM algorithms

另外，2种基于区间箱粒子的SLAM 算法主要的时间消耗在于区间运算，且每个箱粒子都存储并保持自己的栅格地图，对每个箱粒子进行FA智能优化就意味着涉及整个地图的处理，因此，IOBPF-SLAM的运行时间相对于BPF-SLAM 要长一些，但其所需粒子数更少，精度更好。图11进一步展示了IOBPF-SLAM的轨迹估计结果和设定路标的估计结果。移动机器人从“起点”位置（0，0）开始沿着黑色参考路径以蓝色箭头方向顺时针运动一个回环，基于改进的FA智能优化箱粒子所估计得到的运动轨迹能正确跟随由参考点定义的轨迹，并且所有的参考点都包含在定位箱粒子中，因此提供了一致的结果。

图12比较了实验中不同SLAM 算法对于设定路标的位置估计误差。可以看出，移动机器人的整个运动过程中，在改进的智能优化BPFSLAM估计所得的潜在路径基础上，IOBPF-SLAM采用EIKF对环境特征进行估计，虽然有少数几个路标点的位置估计误差大于GMapping，但IOBPFSLAM对整个环境中设定路标的估计精度更高。

图12 不同SLAM算法的路标位置估计误差比较Fig.12 Comparison of estimation errors of landmark position among different SLAM algorithms

图13的地图构建结果进一步展示了IOBPFSLAM生成的二维栅格地图与真实环境一致，其边缘清晰，没有重叠或扭曲，并且在整个过程中程序运行平稳，因此是可行有效的，可为工程应用提供参考依据。

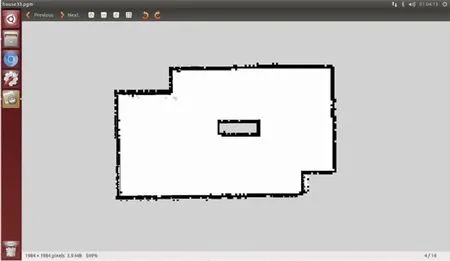
图13 IOBPF-SLAM生成的二维栅格地图Fig.13 Two-dimensional grid map generated by IOBPF-SLAM

5 结论

1）本文算法将区间分析引入移动机器人FastSLAM算法架构中，利用BPF取代传统PF，并通过利用FA的动态寻优机制智能地引导箱粒子集朝着移动机器人的真实轨迹靠近，该策略没有增加额外的操作和参数，保持了算法的简单性。

2）IOBPF-SLAM 可有效解决传统FastSLAM算法需要大量粒子构建地图的问题，同时克服了箱粒子的退化，避免了反复执行随机子划分重采样，因此在粒子数较少的情况下，能够获得良好的定位精度和地图构建精度，且计算量适中，满足实时性的要求。

3）仿真和实验结果表明，IOBPF-SLAM 相较于其他几种SLAM 算法，为移动机器人的同步定位与位姿估计提供了更为精确、可靠的结果。此外，通过对设定路标的位置估计发现，EIKF在计算量方面与传统EKF算法相当，但其滤波效果和鲁棒性相对于EKF有明显的优势。

考虑到BPF具有的性能优势，在后续工作中，将在区间分析基础上进一步结合其他智能优化与学习进化方法改善BPF的性能，并将其应用于复杂环境或其他类型传感器的移动机器人SLAM问题。