基于区间估计与透射率自适应约束的去雾算法

杨燕，张金龙，张浩文

（兰州交通大学 电子与信息工程学院，兰州 730070）

在雾霾等恶劣天气下，由于大气中悬浮粒子等因素的影响，经常导致成像设备采集到的图像产生对比度下降、色调失真等问题，从而给计算机视觉系统的下一步研究造成了严重的影响。因此，对雾天天气下质量受损图像复原问题的研究，具有很大的研究价值和现实意义。

目前，大多数图像去雾算法主要是从大气散射模型出发，通过一些假设条件或者先验信息反演得到去雾结果。例如，He等［1］提出了暗通道先验理论去雾算法，通过多大量户外无雾图像的统计观察，发现无雾图像的暗通道像素值强度至少在一个颜色通道中非常低甚至趋于0，并利用这一先验信息估计出透射率，进而得到复原结果，实验表明，该算法去雾较为彻底，但去雾后图像整体偏暗，且天空等高亮区域出现颜色失真等现象。Tan［2］利用清晰图像与有雾图像对比度之间的差异，结合马尔可夫随机场建立数学模型进行优化处理，虽然该算法去雾较为彻底，但复原结果局部区域存在失真现象。Meng等［3］提出了一种边界约束透射率的去雾算法，并使用正则化来优化透射率，复原结果存在较为严重的偏色现象。Xu等［4］提出了一种结合暗通道和亮通道先验理论的去雾算法，虽然取得了不错的复原结果，但由于透射率估计不准，复原结果局部区域存在失真现象。Yang和Wang［5］提出了一种基于边缘保持函数代替最小滤波拟合暗通道的去雾算法，该算法利用幂律压缩和线性衰减克服了最小滤波的局限性，进而得到了较为准确的透射率，并取得了不错的复原效果。Zhu等［6］以机器学习的方式训练了景深模型的参数，进而获得了透射率和去雾图像，但其结果存在去雾不彻底现象。

近年来，基于深度学习的去雾算法快速兴起。Cai等［7］提出了一种基于端到端的网络模型去雾算法（Dehaze-Net），通过结合复原算法中的假设和先验信息，进而得到复原结果。Ren等［8］提出了一种多尺度卷积神经网络（MSCNN）用以训练透射率，并利用细尺度网络对透射率进行优化，进而得到最终去雾结果。Li等［9］提出了一种多合一网络模型（AOD-Net），将透射率与大气光改写为一个新的函数，利用多层卷积网络来训练得到该新函数，达到了同时训练大气光与透射率的目的，最终得到去雾结果。Liu等［10］构造了一种残差网络结构，并结合有雾图像及其假设或者先验信息，用以估计透射率。Qian等［11］设计了一种颜色提取和深度去雾网络（CIASM-Net），尽管该网络考虑了图像颜色特征，但由于透射率的单独训练，导致其去雾结果仍具不稳定性。虽然基于深度学习［7-16］的图像去雾算法在测试集图像中取得了理想的效果，但是该类算法没有考虑到图像退化的本质，并且由于数据集由合成图像构成，导致其在真实场景下的复原实验中效果较差；另外，大规模的卷积具有非常高的计算复杂度，对实验环境及软硬件要求较高。

为了可以快速且高效地达到真实退化场景的复原处理，本文提出了一种无雾图像最小通道区间估计和透射率自适应约束的去雾算法。根据有雾图像在不同的景深处退化速度不同的特性提出一种衰减模型，并利用有雾图像为约束条件，映射出无雾图像最小通道上边界；根据大气散射模型空间分布关系，建立了一种平面三角形模型，以一种简洁的几何关系获得无雾图像最小通道下边界，进而获得无雾图像最小通道，并得到透射率初始估计。对透射率进行自适应优化，并结合大气散射模型得到去雾图像。实验结果表明，本文算法不仅在真实有雾图像的复原中表现优异，在测试集图像上同样具有理想的复原效果，且算法具有较低的复杂度，在运行时间和其他客观评价指标中均取得了优异的表现。

1 大气散射模型

在计算机视觉系统中，通常以大气散射模型来表现雾天条件下的成像过程，其表达式为

式中：I（x）表示有雾图像；J（x）表示无雾图像；A为大气光值；t（x）为透射率；J（x）t（x）表示入射光衰减模型，反映了反射光在介质中衰减的结果；A（1-t（x））表示大气光成像模型，反映了大气光散射导致成像的现象，从而导致颜色偏移。

在大气散射模型中，只有有雾图像一个已知量，因此必须要借助一些假设条件或者先验信息来辅助无雾图像的求解。根据大气成像理论可知，有雾图像和无雾图像之间存在一定的衰减关系。研究人员利用这一特性，结合各种衰减函数，从有雾图像最小通道出发，去拟合出无雾图像的最小通道，进而估计出透射率，最终根据大气散射模型得到复原结果。

2 本文算法

大气散射模型中，估计透射率的关键是获得较为准确的无雾图像最小通道。通常，研究者倾向于利用有雾图像最小通道的衰减去拟合无雾图像最小通道，但衰减函数及其参数的选择是比较困难的，不同特征的雾图其参数往往不同。根据大气成像理论，雾天图像退化在远近景区域具有不同的程度，本文提出了一种基于有雾图像最小通道约束模型，以估计无雾图像最小通道，从而得到透射率。大气光的准确性往往影响着复原结果的亮度信息，本文借助有雾图像不同尺度的亮通道获得大气光，最终根据大气散射模型得到复原结果。本文算法原理框图如图1所示。

图1 本文算法原理框图Fig.1 Block diagram of principle of proposed algorithm

2.1 大气光

根据大气成像理论，大气光的准确度往往对复原结果的明度信息具有较大的影响。文献［17］指出，大气光的估计往往影响到复原结果的明暗度；若大气光估计过高，会造成复原结果远景较暗，近景较亮；若大气光估计过低，会造成远景较亮，近景较暗。局部大气光对最大通道进行单一尺度的处理，可能导致大气光定位不准。受到局部大气光探索方法［18］的启发，本文对大气光作如下改进：在RGB通道提取其不同尺度的亮通道Ibright1（x）和Ibright2（x），最大滤波尺寸分别为3×3和10×10，并对不同尺度亮通道做如下处理：

大气光应该准确地反映大气光照信息，为了消除局部过亮现象，利用形态学模糊处理有雾图像亮通道。形态学处理中先膨胀后腐蚀可以突出比原图轮廓区域更暗的区域，并将2个区域连接起来，形成连通域。为了操作方便，数字图像处理中一般用闭操作代替膨胀腐蚀处理，则

式中：se为形态学处理参数；本文选取闭操作滤波核为min（W，H）/15，W和H为原图尺寸。

形态学处理虽然在一定程度上消除了局部过亮现象，但是经过形态学处理后可能引入噪声和细纹理等信息，导致复原结果局部细节丢失。因此，本文引入高斯滤波对A0（x）进行消噪处理。二维高斯滤波传递函数为

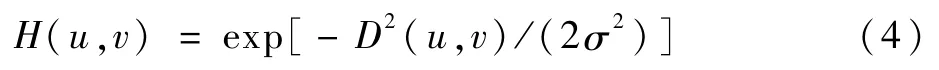
式中：D表示距频率矩形中心的距离；u、v为坐标，决定着滤波器形状的方差σ2，标准差σ决定着滤波后图像的平滑程度，其越大，平滑程度越好。

经过消噪处理后大气光为

通过实验发现，引入高斯滤波后大气光信噪比大幅提升。最终利用交叉双边滤波处理消除纹理，从而得到本文大气光。本文大气光与局部大气光对比示意图如图2所示。可以发现，局部大气光局部估计过高，导致复原结果亮度不准确，本文大气光复原结果亮度自然。

图2 大气光对比Fig.2 Comparison of atmospheric light

2.2 最小通道估计

2.2.1 最小通道下边界估计

文献［14］指出，大气散射模型的空间分布如图3（a）所示，在RGB空间中，大气光、有雾图像、无雾图像共平面且模长依次递减，为了便于分析各量之间的关系，将该分布图映射到二维平面中，如图3（b）所示，由大气成像理论可知，有雾图像I（x）和无雾图像J（x）之间存在某种衰减，进一步，将二者关系简化为图3（c）所示。

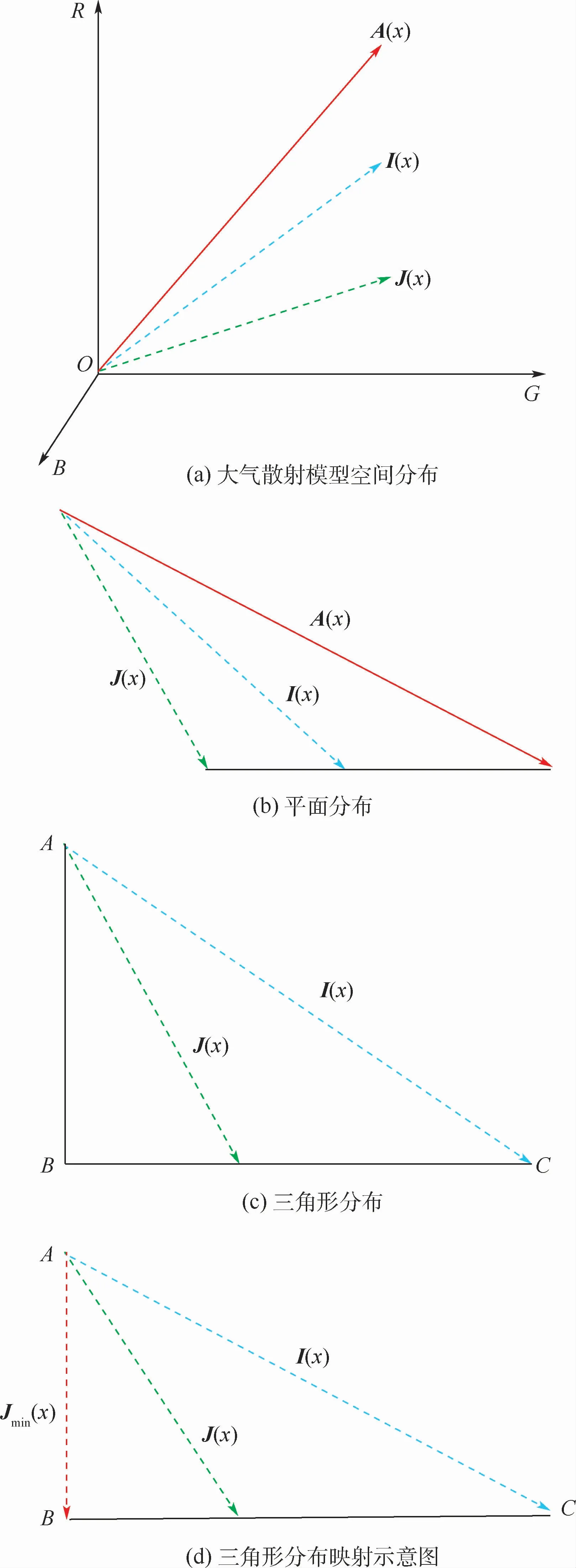
图3 大气散射模型空间分布与简化分布Fig.3 Spatial distribution and simplified distribution of atmospheric scattering model

在△ABC中，根据几何知识可知，当无雾图像J（x）的最小通道达到最小值即下边界时，△ABC为直角三角形，且此时最小通道下边界正好为AB的模长；而三角形中存在如下关系：任意两边之和大于第三边，任意两边之差小于第三边，即

代入各矢量，有

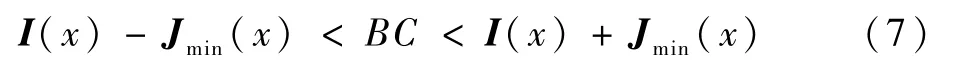
对于有雾图像和无雾图像最小通道，则有

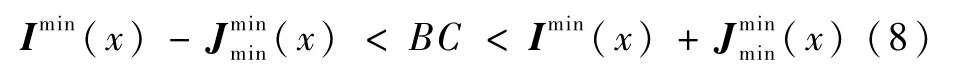
式中：Imin（x）为有雾图像最小通道；为无雾图像最小通道下边界。

在式（8）中，若要准确得到BC，则不等号右边应尽可能得小，而左边应尽可能得大，因此，将式（8）进一步推广可得

式中：Idark（x）为有雾图像暗通道。

为简化计算，现构造关于BC的等式约束为

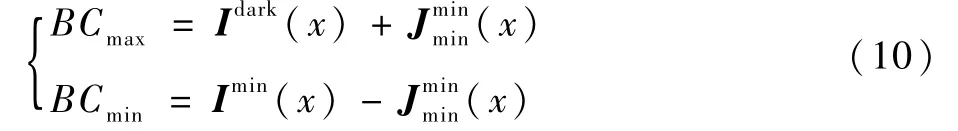
取BC最大值和最小值的调和均值作为BC的最终估计值，即

则在△ABC中，根据勾股定理，无雾图像最小通道的下边界值为

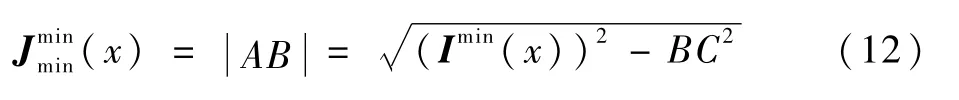
将大气散射模型的空间分布转至平面三角形分布，利用三角形三边关系和勾股定理可以非常简洁地获得无雾图像最小通道的下边界。

2.2.2 最小通道上边界估计

在均匀介质中，透射率被定义为

式中：β为散射系数；d为景深。

由于在大气中，影响能见度的主要因素来自于粒子的散射作用，而吸收造成的影响很小，通常认为散射系数与波长无关，则影响透射率的主要因素就是景深d。可以看出，在雾天场景下，透射率随景深减小，此时成像设备采集到的图像模糊程度增大，即景深越深处，从有雾图像到无雾图像之间的衰减越快；相反，在景深较小处，透射率大，受损图像的模糊程度越小，此时从有雾图像到无雾图像具有较慢的衰减速度。

综上分析可得，景深对退化图像的影响极大。根据式（13）可得，随着景深增加，图像退化的速度增大。即在天空等景深处具有较快的衰减速度，近景区域衰减较慢。本文根据这一特性，将有雾图像最小通道作为约束条件，建立一种满足上述特性的映射函数，并求取无雾图像最小通道的上边界。从数学角度分析，该映射模型在近景区域应该满足变化率平缓，在远景区域变化率稍微剧烈，即该模型应该满足以下条件：①从有雾图像最小通道到无雾图像最小通道的映射为一一映射，不能发生像素值溢出现象，将图像归一化处理后，映射模型的值域和定义域都应该为［0，1］；②在近景区域应该缓慢映射，在远景区域稍剧烈映射，且考虑到归一化图像的特性，这种映射应该是相同区间的映射，则将映射模型定义为

为了验证该模型在近景和远景处具有不同的变化率，对其进行一阶导数分析，其导数表达式为

映射模型与其导数图像如图4所示，导数反映了映射模型在不同取值处的变化速率。可以看出，当自变量较小时，映射模型具有较为平缓的映射速度；当自变量逐渐增大，映射速度也增大。

大气散射模型中，存在如下关系：则根据映射模型可得，无雾图像最小通道上边界估计值为

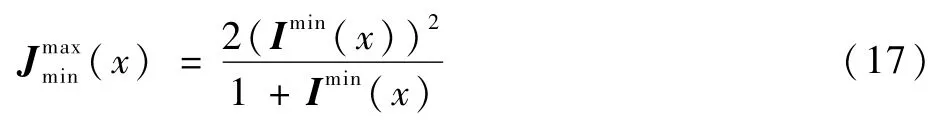
综上，通过平面三角形模型获得无雾图像最小通道下边界，利用自适应映射模型获得无雾图像最小通道上边界，即无雾图像最小通道区间如下：

平面模型获得无雾图像最小通道下边界主要是针对一般场景，而映射模型获得上边界在景深图像表现出了更优的性能，为了最小通道信息不丢失，将上下边界估计值均匀地应用到去雾场景。本文利用几何均值对最小通道的上下边界进行处理，进而获得本文无雾图像最小通道，即

如图5所示，为了验证所提模型的准确性，选取RESIDE数据集中的5幅图像进行验证，包括2幅纵深图像（图像1～图像2）、2幅近景图像（图像3～图像4）、1幅远近景交替图像（图像5）。验证算法如下：

算法1模型准确性验证。

输入：数据集标签，数据集合成有雾图像。

输出：标签对应最小通道Jmin（x），所提模型拟合结果。

步骤1求取有雾图像I（x）的RGB三通道最小通道Imin（x），并代入本文所提约束模型获得无雾图像最小通道估计量。

步骤2求取数据集标签RGB三通道标准最小通道Jmin（x）。

步骤3求取拟合结果与标准最小通道Jmin（x）的差值，令ω=。

步骤4分析像素差值ω，ω越小，表明所提模型越准确。

随机选取的5幅图像中，利用算法1分别验证近景、中景和远景区域。所选图像真实最小通道与本文所提模型最小通道对比如图5所示，分别求取远景、近景和中景区域的误差均值，结果如表1所示。实验表明，本文所提衰减模型具有较为理想的处理效果，拟合结果与真实值误差整体较小，进一步表明了无雾图像最小通道上边界估计的准确性。

表1 远近景区域误差ωTable 1 Near-and far-field regional errorω

图5 最小通道真实值与本文拟合结果对比Fig.5 Comparison of true value of minimum channel with fitting results of this paper

为了进一步说明本文最小通道估计的准确性，将与DCP算法所得无雾图像暗通道进行均方误差（MSE）对比。真实环境下的有雾图像缺少标准的无雾图像，因此选择合成图像集作为实验对象，任意选取Middlebury数据集中的5幅图像进行MSE对比，MSE表达式如式（20）所示。本文模型与DCP算法在数据集中的评分如表2所示。可以看出，本文所提模型更加准确，而DCP算法将无雾图像暗通道在所有区域均设为0，导致对于天空等区域产生较大的误差。

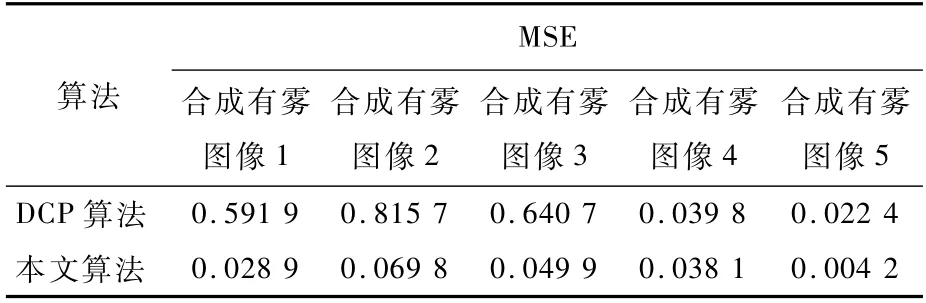
表2 MSE指标对比Table 2 Comparison of MSE indicators

式中：Jdark（x）为标准无雾图像暗通道为无雾图像暗通道估计量；N为总像素个数。

2.3 透射率

根据大气散射模型可得，透射率表达式为

联立式（19）、式（21）可得本文初始透射率。透射率作为复原模型中的重要参数，对复原结果影响极大。He等［19］为了细化透射率，使用了导向滤波并取得了不错的效果，但这种方法在消除光晕的同时，保留了残雾。为了防止透射率局部区域发生下溢出的现象，研究者对透射率都做了下边界定值约束的处理，但这种处理太过局限，是导致天空区域发生颜色失真的原因之一。

透射率表示光线在雾气影响下的穿透能力，天空等远景区域雾浓度较高，透射率则较小，但根据先验信息估计的透射率往往对天空区域偏小，甚至会发生天空区域透射率为0的现象，将造成复原结果在天空区域的像素溢出，表现为颜色失真等。而定值约束会将大片天空区域设为同一透射率，这种方法同样导致复原结果天空局部失真。

为了解决此问题，本文进行透射率优化处理时，对其先进行自适应边界约束，后采用双边滤波进行平滑处理。为此，本文对初始透射率进行最小值操作，得到透射率的下边界通道图，即

式中：Ω为局部窗口，为了保证下边界通道T（x）更加模糊，本文选择20×20的滤波窗口。

求取T（x）的灰度均值k作为下边界约束值，即

透射率图的灰度值往往较小，即k值很小，但当有雾图像中包含较多天空等高亮区域时，k值自适应增大，对于天空等透射率估计偏小的区域，k值将自适应地增大天空等区域透射率，进而克服天空颜色失真的现象。则透射率为

相较于导向滤波，交叉双边滤波在消除纹理的同时还可以保持更丰富的边缘信息，因此，对式（24）所得透射率进行交叉双边滤波处理，从而得到本文透射率。为了说明本文算法透射率估计的准确性和普适性，选取2组真实环境下的有雾图像进行透射率分析，选择经典复原算法DCP算法进行比较说明。含有天空区域对比如图6所示。可以看出，DCP算法由于在天空区域的失效性和最小滤波求取暗通道的原因，导致其复原结果在天空区域发生了严重的偏色现象，在天空和山的交界处出现了明显的光晕和伪影，且由于其透射率局部估计过小，导致DCP算法的复原结果存在局部区域的过饱和现象，如图6所示的3幅图像均出现了这种情况。本文算法以映射模型获得无雾图像的最小通道估计，克服了DCP算法无雾图像为0的局限性，获得了更加准确的透射率，复原结果去雾彻底、亮度适宜，颜色自然，且克服了光晕现象。对于不含天空区域的有雾图像，由于暗通道出现的伪影和光晕，导致DCP算法的复原结果同样出现了光晕等问题，如图7中第3幅图像的树叶周围。尽管不含天空的无雾图像暗通道趋于0，但事实上近景明亮区域的暗通道依然不为0，而是一个相较于0较大的值，因此DCP算法对近景区域透射率估计仍然不够准确，导致其复原结果在近景明亮处失真较严重，且丢失了图像局部细节信息，如图7中第1幅图像的人脸和衣服。本文算法从图像全局出发估计无雾图像最小通道，无论是近景明亮区域还是正常亮度区域，都得到了较为准确的透射率，因此本文复原结果细节更加清晰，颜色更加自然。

图6 含天空区域图像透射率与复原结果对比Fig.6 Comparison of transmittance and restoration results in sky-images

图7 不含天空区域图像透射率与复原结果对比Fig.7 Comparison of transmittance and restoration results in no-sky-images

为了进一步验证本文透射率估计的准确性，随机选取公开数据集RESIDE中的1幅室内图和1幅室外图进行验证，根据大气散射模型，在已知无雾图像、大气光、有雾图像的条件下可以反推出透射率，本文透射率和标准透射率对比如图8所示。可以看出，本文透射率估计非常接近标准透射率，且取得了理想的复原效果。

图8 本文透射率与标准透射率对比Fig.8 Comparison of transmittance in this paper and standard transmittance

3 实验结果

根据大气散射模型可得复原模型为

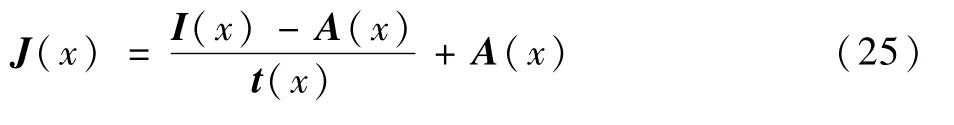
代入本文所求大气光与透射率可得复原结果。

为了验证本文算法的有效性和可行性，从主客观2个角度和经典去雾算法进行对比分析。所选算法为He等［1］的DCP算法、Yang等［5］的Haze Removal算法、Zhu等［6］的CAP算法、Cai等［7］的Dehaze-Net算法、Ren等［8］的多尺度提取算法、Li等［9］的AOD-Net算法。

3.1 主观评价

为了说明本文算法的宽适性，分别从真实雾图和合成雾图2个角度进行主观对比分析，随机选择Middlebury图像集中的5幅图像和RESIDE数据集中的5幅图像进行测试集验证。主观对比可以直观地看出算法的有效性。选择2组含有不同特征的有雾图像进行主观对比，不含天空区域复原和含天空区域复原，对比结果分别如图9和图10所示。测试集复原结果如图11和图12所示。

图9 不含天空区域复原结果对比Fig.9 Comparison of restoration results without sky area

图10 含天空区域复原结果对比Fig.10 Comparison of restoration results with sky area

图11 RESIDE测试集验证结果Fig.11 RESIDE test set verification results

图12 Middlebury测试集验证结果Fig.12 Middlebury test set verification results

通过对比发现，DCP算法［1］对于非天空或非白色区域整体处理效果较好，但复原结果存在一定的光晕效应；对于天空或白色区域由于透射率估计不准，导致复原结果产生了严重的偏色现象。Haze Removal算法［5］以一种新的边缘保持函数代替最小滤波，克服了最小滤波带来的块效应等问题，去雾彻底且颜色保持较好，但对于浓雾区域，存在轻微去雾不彻底现象。多尺度提取算法［8］与AOD-Net算法［9］在一定程度上克服了天空区域的颜色失真问题，但整体偏暗，且无论是近景区域，还是天空区域，都存在去雾不彻底的现象。本文算法从大气散射模型出发，通过所提映射模型进行透射率估计，复原结果整体较为理想，克服了颜色失真和光晕等现象，且去雾彻底，亮度适宜。但对于某些浓雾图像，本文算法产生了轻微的发暗现象。综上所述，本文算法对于真实环境下的有雾图像具有较为理想的处理效果。从图11和图12可以看出，在Middlebury测试集和RESIDE测试集上，本文算法同样表现出了较为优越的性能。可以看出，无论是室外合成图，还是室内合成图，本文算法均取得了理想的去雾效果，去雾图像亮度适宜，颜色自然，且由于测试集无雾图像在获取的时候本身带有一定的雾气影响，本文算法对于测试集图像复原效果更佳。

3.2 客观评价

尽管主观分析可以直观地看出各算法的差异与不足，但仍具片面性。为了进一步说明本文算法的可行性，将从客观指标方面与上述经典算法进行对比分析。本文客观评价指标采用在图像领域应用较为广泛的无参考图质量评价方法［20-23］，选择直方图相似度HCC、图像熵E、图像对比度CG、视觉对比度VCM 和通用质量指数UQI为客观评价指标，HCC主要是衡量图像直方图分布相似性的指标，E是指图像的平均信息量，该指标从信息论的角度衡量图像中信息的多少，图像中的信息熵越大，说明图像包含的信息越多，CG 体现了复原图像的色彩度，VCM体现了视觉可视度。在测试集验证结果中使用全参考图评价方法［21］，选择峰值信噪比（PSNR）与结构相似性（SSIM）进行客观分析，其数学表达式如下：

式中：Pi为图像中某灰度级出现的概率；Cj和Ci分别为无雾图像和有雾图像的平均对比度；Rv为图像局部区域像素值大于一定阈值的数量；Rt为图像局部区域像素总数。上述指标评价原则为HCC、E、CG、VCM 和UQI越大越好。

对真实环境下的有雾图像进行式（26）～式（29）的客观指标分析，客观评价如表3所示。测试集客观指标对比如表4和表5所示。为了体现各算法复杂度，利用运行时间进行对比分析，将输入图像尺寸统一为480×320，再进行时间复杂度对比。表3中：T为运行时间。

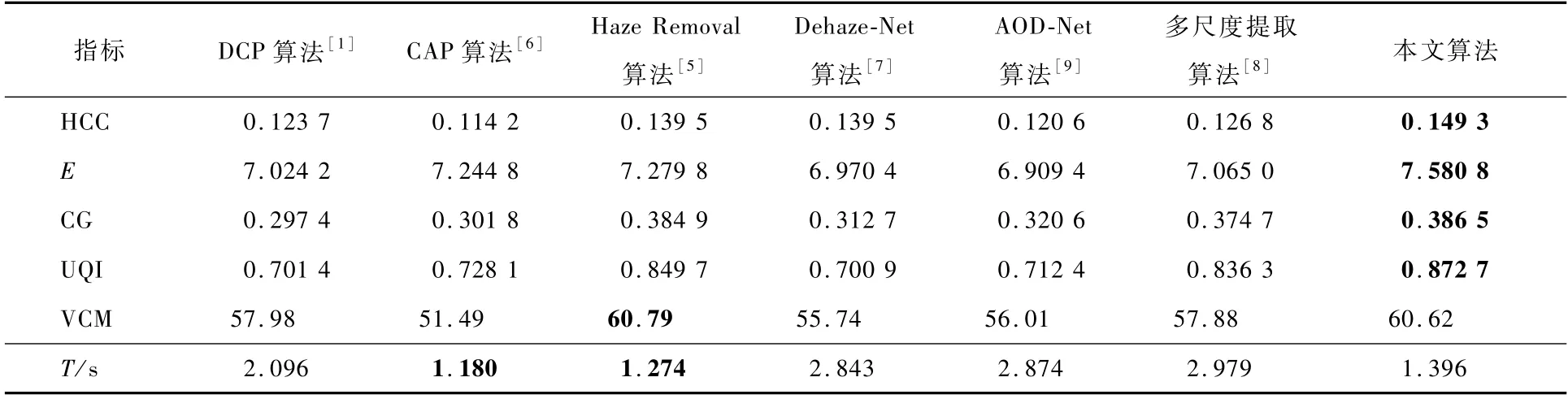
表3 真实有雾图像复原结果客观指标对比Table 3 Comparison of objective indicators of true hazy image restoration results

表4 Middlebury测试集复原结果客观指标对比Table 4 Comparison of objective indicators of Middlebury test set restoration results

表5 RESIDE测试集复原结果客观指标对比Table 5 Compar ison of objective indicator s of RESIDE test set restoration r esults

结合主客观评价可知，相较于DCP算法［1］与CAP算法［6］，本文算法透射率估计更加准确，复原结果克服了光晕和颜色偏移等问题，因此本文算法在客观指标上都领先于DCP算法和CAP算法；Haze Removal算法［5］以一种边缘保持函数代替最小滤波，取得了不错的效果，客观指标与本文算法接近。CAP算法［6］在时间复杂度上取得了优势。Dehaze-Net算法［7］、多尺度提取算法［8］与AOD-Net算法［9］是基于神经网络模型去雾的，其中多尺度提取算法［8］客观指标较为理想，但仍落后于本文算法。从表4和表5可以看出，本文算法在测试集也获得了理想的表现，在SSIM 和PSNR上均取得了较高的评价。综上，本文算法在主客观2个角度，无论是真实有雾图像，还是测试集合成有雾图像，均具有理想的处理效果。

4 结论

针对去雾算法中无雾图像暗通道估计不足与复原结果失真等问题，本文提出了一种基于最小通道与透射率自适应约束的去雾算法，主要贡献如下：

1）对于局部大气光的不足进行了改进，克服了单一尺寸与局部过亮导致的复原结果亮度失真问题，并利用高斯滤波对其进行降噪处理，得到了更加准确的大气光。

2）根据大气散射模型空间关系，获得了简洁的平面三角形模型，并根据几何关系得到无雾图像最小通道下边界估计；从雾天图像退化本质出发，以一种自适应衰减模型获得无雾图像最小通道的上边界，进而获得最终最小通道图，并分别从像素误差、均方误差等方面进行了所提模型准确性的验证。

3）针对传统去雾算法透射率下边界定值约束的不足，提出了一种自适应下边界约束的方法。

实验表明，本文算法对于真实环境下的有雾图像和合成有雾图像都有较好的处理效果；在主观分析上去雾彻底，复原结果图像亮度适宜，颜色自然，消除了光晕和颜色偏移等现象；在客观指标上也取得了优势。