微探究活动中的预设与生成——以一道习题教学为例

广东省广州市第二中学(510040) 邹 芬

数学探究教学一般是指学生围绕某个数学问题,进行自主学习,探究结论,提出数学问题,使用数学解决问题的过程.数学探究对学生学习态度,学习能力有着较高的要求,对于八年级的普通学生来说,完全自主的探究活动往往流于形式,收效甚微[1].基于学生的实际情况在课堂教学中教师往往针对课堂的某个环节开展教师主导下的微探究活动.微探究注重的是组织学生开展数学问题探究,在这个探究过程中,以教师为主导,学生为主体,数学是载体,思维是形式,以此培养学生的主动性、创造性、应用意识和实践意识[2].在教学微探究中,教师的问题设计既是教师主导课堂的体现,也是推动学生进行探究活动的催化剂,但是课堂教学往往不会完全遵循教师预设的问题设计开展,教学过程中教师要善于发现学生闪现的新想法,呈现的新思路,捕捉学习探究活动中的瞬间生成,并及时调整问题设计,才能激发学生的探究欲望,激发学生主动思考数学,内化数学思想方法,提升数学素养[3].

以下通过笔者在两个班先后讲评同一道课本习题的课堂实践为例,谈谈微探究课堂问题设计的预设与生成.

1 课堂实践一与反思

习题如图1 所示,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°.EF交正方形外角的平分线CF于F,求证:AE=EF.

图1

教材和学情分析本题来自于人教版数学八年级下册第69 页“四边形”复习题18 拓广探索第14 题.课程实施对象为数学成绩中等班级,学生基础知识扎实,学习积极性较高.在本章之前学生已学习了“全等三角形”,“轴对称”、“勾股定理”、“四边形”等章节,在“四边形”这一章的学习过程中,大部分学生对条件齐全的全等三角形的证明能熟练掌握,并能利用全等三角形对应边相等,等角对等边及勾股定理等来求证线段相等,但对如何添加辅助线存在一定的困难.

案例实录:

师: 由已知条件“点E是边BC的中点,EF交正方形外角的平分线CF于F”,我们能找到哪些相等的线段和相等的角?

生1:BE=EC,∠DCF=∠FCG.

师: 非常正确,能将题目中的条件转化为具体的边角关系将有助我们进一步探索.

反思: 当题目出现在屏幕上时,教师自己将问题朗读了一遍,优点是加快课堂节奏,明确问题导向,有助于教师顺利实现课堂预设.但是,教师以自己的行为代替了学生对问题的自主理解,教师对问题的理解并不意味着学生已经把握好问题的条件和目标以及问题所涉及的相关概念,而理解问题、明确任务恰恰是解决问题的第一步! 这一步的不足,直接影响学生解题能力的提高.

师: 题目要求证明线段相等,我们证明线段相等最常用的方法是什么?

生2: 利用全等三角形来证明线段相等.

(学生3 在座位上喊出:“等腰三角形也可以”.)

师: 非常好! 我们常常利用全等三角形来证明线段相等,图中以AE、EF为边的三角形全等吗?

反思: 利用全等三角形证明线段相等是学生非常熟悉且比较直观的一种方法.但是,就题讲题,拘泥于把问题讲清楚,是远远不够的.由于在特殊的平行四边形里由对角线分割出等腰三角形,直角三角形也是本章的相关教学内容,教师需要通过讲题加强知识横向联系,有助于学生建构知识体系.以本题为例,还可以通过构造直角三角形、等腰三角形等其它方法予以证明.特别是学生3 说到利用等腰三角形证明线段相等时,教师需要关注到学生不同的思维方向,有效的课堂要有精心的课前预设,更要重视课堂的生成,在教学过程中因势利导,引导学生拟订求解计划,不仅可以加深对知识体系的认识,还可鼓励学生参与课堂探究,提高学习积极性.

师: 嗯,同学们对图形的识别能力很强,ΔABE与ΔECF不全等,那我们尝试构造一对全等三角形从而得到AE=EF吧!

生4: 作FH⊥BC交BC的延长线于H,ΔABE与ΔEFH看上去挺全等的.

师: 很多同学想到作FH⊥BC交BC的延长线于H(如图2 所示),接下来我们看看能否找齐全等所需要的条件?

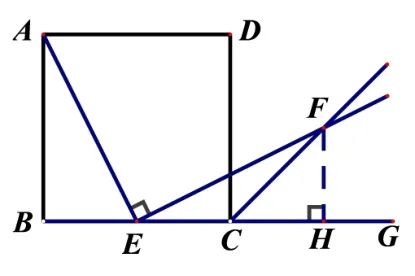
图2

生5: 由题目可知: ∠B=∠EHF=90°,由∠AEF=90°,∴∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF.

师: 很好,我们已经发现证明全等所需的3 个条件中的两个,胜利在望了.

反思: 教师在教学过程中能对学生的思考给予正向的回应,并在解答过程中不断给予肯定,刺激学生继续积极思考,树立学生解决问题的信心,从而自主找出全等所需的两对对应角,这个过程学生经历了自主探索知识的过程,体现了学生的主体地位.

师: 接下来,我们还需要什么条件?

生5: 要是能有AB=EH就好了.

生6:E是BC的中点,如果C是EH中点也可以证的.

师: 但本题中有这个条件吗? 证明AB=EH难度较大,我们需要换一种思路.

反思: 在教学实践中发现,图2 是学生最常想到的作辅助线的方法,但常常没能“此路不同,另辟蹊径”地寻找另外的解题策略,从而导致解题失败.在此处,换种思路是克服实现求解计划中遇到的困难的一种方法.而寻求AB=EH的求解计划则是本题中再一次激发学生拓广思维宽度的契机.因此,教师在课前预设时需要准备更充分,尊重学生的理解和方法,顺应学生的需要,引导学生寻求有效的解题计划的策略与方法.

师: 既然得不到ΔABE与ΔEFH全等,我们再构造一个与ΔECF全等的三角形吧! 如图3 所示,取AB中点M,连ME,得到ΔAME.

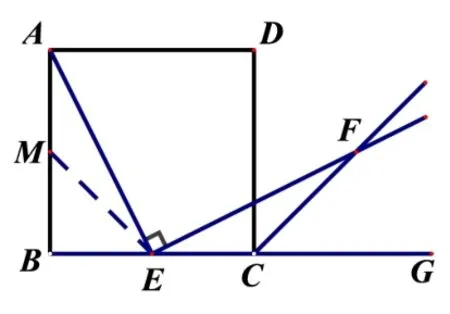
图3

生7: ∵M、E为正方形ABCD边的中点,∴AM=EC,……∴ΔAME∽=ΔECF,∴AE=EF.

师: 太棒了,我们常常通过构造全等三角形来证明线段相等.课后同学们可以继续思考如图4,若将点E变为BC边上的任意一点,其它条件不变,是否仍然有AE=EF成立?

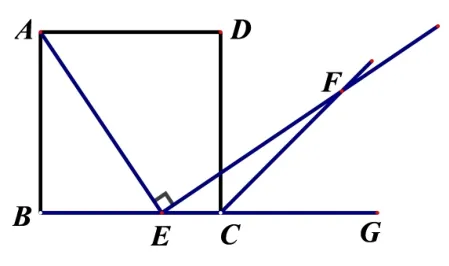
图4

反思: 教师的讲题到此就结束,问题看似完整解决,但是从课后练习发现大部分学生依然选择与图2 类似的辅助线,不能顺利解决问题.课堂探究的效率高低不取决于教师打算教给学生什么,而取决于学生实际学到什么,思维获得什么发展.问题探究是学生经历数学再创造的过程,是数学思维过程的展现.数学微探究评价的重点是课堂的教学效果.教师在问题设计时要总结自己的思维过程,更要站在学生的视角审视学生在解决问题过程中会遇到哪些困难,问题设计要重在帮助学生突破自己思维上的障碍,进行数学思考,使用数学思想方法解决问题.

2 课堂实践二

基于课堂实践一的反思和对微探究课堂问题设计的思考,笔者在第二个班讲评这道习题时,对理解问题与明确任务、提出假设与设计解决方案、检验和回顾等三个环节加以改进.

2.1 理解问题与明确任务

对该环节的改进如表1 所示.

表1 理解问题与明确任务

这一阶段限时5 分钟.通过巡堂发现学生有如下几种表现:

情况1: 找出正方形中四条边相等,四个角是直角.

情况2: 标记线段BE=EC,∠FCG=∠DCF.

情况3: 标记线段BE=EC、∠FCG=∠DCF,且连线段AF,在努力求证∠EAF=∠AFE,试图通过等角对等边从而得到AE=EF.

情况4: 标记线段BE=EC、∠FCG=∠DCF,标记直角∠AEF,作FH⊥BG,试图证明ΔABE∽=ΔEFH.

情况5: 连AF,标记BE=x,AB=2x,并运用勾股定理算出AE=

情况6: 作AB中点M,构造ΔAME,思维流畅清晰.

可见学生从题目获取信息的能力有较大区别,思维方向比较发散,意味着学生在理解问题、理解探究对象这一步骤存在较大差异,提出假设和设计解决方案也具有一定的差异性.

2.2 提出假设与设计解决方案

对该环节的改进如表2 所示.

表2 提出假设与设计解决方案

生1: 设BE=EC=x,则AB=2x,只需证明CH=EC=x即可.

师: 将要证AB=EC+CH,转为证明CH=EC=x,形式更加简洁,更容易入手.如何证明呢? 继续用全等三角形吗?

生2: 不能用全等三角形了,那两个三角形看上去就不全等.

生3: 不用全等三角形还能证线段相等吗?

师: 再想一想,你还用过哪些方法证明线段相等?

生2: 哦! 勾股定理.

生4: 还有等腰三角形呢!

师: 这些都是我们常用的方法,现在你们想尝试用哪种方法证明CH=EC呢?

生2: 等腰三角形肯定不行,CH、EC都构不成三角形.

生1: 那就用勾股定理试试吧!

师: 在哪些图形中可以运用勾股定理呢?

生5: 直角三角形中,有

学生经过小组讨论、交流、合作整理出如下解法(如图5 所示):

图5

解法一设CH=FH=a,在RtΔEFH中,有EF2=(x+a)2+a2=x2+2a2+2xa,在RtΔABE中,有AE2=(2x)2+x2=5x2,在RtΔACF中,有AF2=AC2+CF2=(AB2+BC2)+(CH2+FH2)=8x2+2a2,在RtΔAFE中,有AE2+EF2=AF2,即5x2+x2+2a2+2xa=8x2+2a2,所 以a=x,即CH=FH=x,可得AB=EH,证得ΔABE∽=ΔEFH,即AE=EF.

解法二同解法一证得a=x,代入勾股定理等式中EF2=(x+a)2+a2=x2+2a2+2xa=5x2=AE2,即AE=EF.

如果在问题设计中过于偏重预设,只有教师的表演,学生仅仅被动接受,课堂的生成被压制忽视,学生的主体性没有得到重视,其有效性必然降低.开展微探究活动需要从学生的个体差异、思维特点出发,关注学生的思维动向,从而激发学生继续探究的欲望,自主参与到探究过程.微探究课堂中教师是主导,在捕捉探究活动的瞬间生成的同时,也要在探究中发挥教师的主导作用,促进完善学生的数学认知结构,提高学生问题解决的能力.在课例2 中教师继续通过问题设计引导学生进一步探究构造全等三角形证明AE=EF,学生通过对比两种解法,整理归纳思想方法,为后续的探究活动打下基础.

2.3 检验和回顾

对该环节的改进如表3 所示.

表3 检验和回顾

通过问题设计引导学生思考: (1)如果这个条件不满足,又如何? (2)交换条件和结论得到的命题是真命题吗? (3)你还能得到哪些结论? (4)这个结论你能推广到其它图形中吗?由此,学生的思维不再局限于解决单个题目本身,而是放眼探索解决一类问题的方法,体会数学思想在解题中的运用.

从课后作业中,发现学生通过思考探究提出了很多想法,例如:

(1)若AE=EF,那么AE⊥EF成立吗?

(2)E为直线BC上一点,结论还成立吗?

(3)将正方形ABCD变为正多边形,情况又如何:

①如图6 所示,等边ΔABC,CF为ΔABC外角平分线,E为BC边上一点,∠AEF=60°,结论AE=EF成立吗?

图6

②如图7 所示,正五边形ABCDM,CF为其外角平分线,E为BC边上一点,∠AEF=108°,结论AE=EF成立吗?

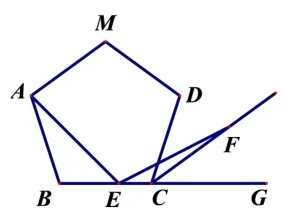
图7

③如图8 所示,E为正n边形边BC上一点,CF为正n边形外角平分线,当∠AEF为多少度时,AE=EF成立?

图8

3 总结

在数学微探究活动中,教师的参与至关重要,教师需要对学生在发现、提出、分析、解决问题等环节进行有效指导.基于课堂生成的问题串的设计更能提高学生对课堂的参与度,激发学生探究的积极性,使学生获得成功感.与此同时,教师也要关注探究活动的主体—学生.问题设计不是指导学生如何探究,而是引导学生参与探究活动.问题既要围绕问题解决进行预设,也要及时捕捉课堂生成,关注学生瞬时的学习状态,顺势而为: 学生当下想到什么? 学生的假设是否成立? 学生在解决问题中遇到什么困难? 如何才能调整学生的思考过程和方向? 引导学生开展自然生成的探究活动,才能达到生态互动,激活课堂.

数学微探究活动根据课堂的实际需要设计启发性的问题,引导探究活动围绕既定目标开展,并关注、尊重学生的思维差异,让学生参与课堂探究,经历数学的产生过程,积累数学活动经验,使不同类型不用层次的学生都能获得发展,提高学生思考和解决问题的能力,数学微探究课堂问题设计中预设与生成的和谐统一既保留了原生态的课堂,也是课堂中“看不见的手”引导学生主动思考,自主探究,从而实现课堂在知识纵横发展的广度和数学思想拓展延申的厚度上的提升.