题目“变式”应谨慎

贵州省遵义市航天中学(563000) 闵 玲

贵州省仁怀市第二中学(564501) 王 俊

1 提出问题

人教版八年级《数学》上册第85 页课题学习“最短路径问题”的问题1 是: 如图1,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地.牧马人到河边的什么地方饮马,可使所走的路径最短?

图1

如图2,课本中的解法是应用轴对称,把河岸看作直线l,找出点B关于l的对称点B′,连结AB′交l于C,连结BC,因为点C到点A,点B距离之和AC+CB最小,则点C是饮马的位置.(证明略).这是初中几何中重要的几何极值问题,数学上一般把它称作“将军饮马”问题.常用来解决生活中的油气管道铺设,输水管道铺设、修路、修水渠等实际问题的最短路径规划设计.同时也成了各地中考及各种考试的一个新宠,常以各种背景加以变式改编,以新面孔出现.一般都是应用对称思想加以解决,如下面的问题.

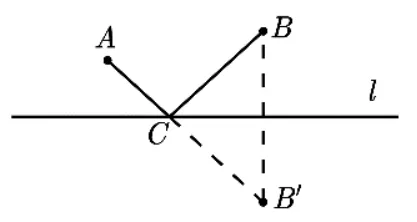
图2

2 质疑问题

问题如图3,在河流l的同侧有A、B两个村庄,AB=16km,它们到河流l的距离分别为4km、10km.供水公司要在河边修建一座供水站,向A、B两个村庄供水,怎样确定供水站E的位置使所铺设的供水管道总长度最短?

解如图3,作点A关于直线l的对称点A′,连接BA′,交直线l于点E,由轴对称性质易知,此时EA+EB=A′B,而根据“两点之间,线段最短”,A′B即为供水管道总长度EA+EB的最小值.

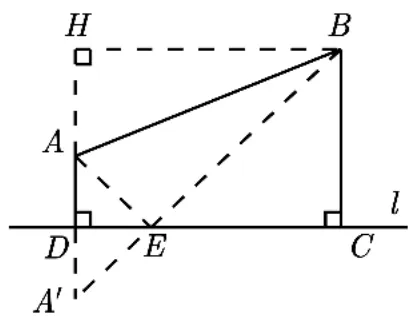
图3

过点B作BH⊥DA交DA的延长线于点H,在RtΔA′BH中,由勾股定理得

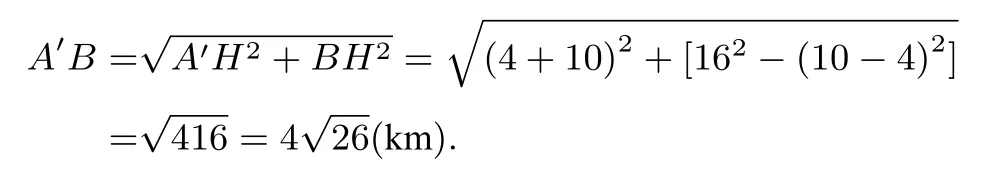
这道题目一般是按照这种作轴对称的方法解决,即认为铺设管道AE+EB是最短的,实际上不一定,这样的反例很好找.如图4,当A、B的连线几乎与l垂直时,显然供水站应建在垂足点C处,管道路线为C →A →B显然比应用轴对称得到的路线短.在实际生活中,水管所采用的实际铺设不一定是这种“V”字形方式,存在不符合实际的情形.从供水(气,油等)源处,向两地A,B供水管道铺设的常用方法是(如图5)或D →A →B(如图6)方式,只要能达到目的,总长最短,都是首选的方式.为方便下文研究,把这三种铺设方式分别称为“V”、“Y”、“厂”字形.实际上,在这个问题中,通过网络画板作图测量、计算,如图7 中的“厂”、和“Y”字形铺设方式都比“V”字形铺设方式短,其中的点F怎么确定,下文将进行说明.

图4

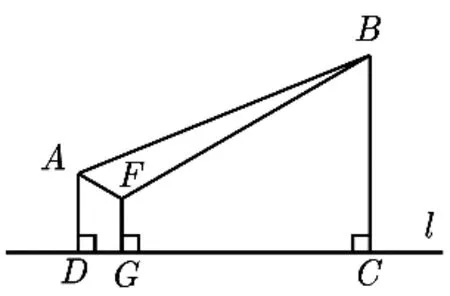
图5

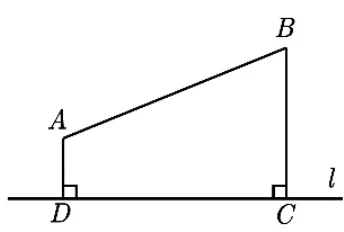
图6

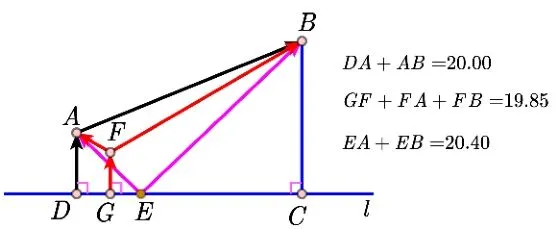
图7

“厂”字形和“V”字形铺设实际是“Y”字形铺设的特殊情况,如图5,当FG+FA+FB取最小值时,有FG⊥l(包括点F在l上的情况).因此问题解决的关键是点F的选择而非点G的选择,当点F选定后,点F在l上的垂足即为点G,因此把这个问题一般化后即为下面的问题.

3 转化问题

在直线l的同侧有A、B两点(设A、B两点的距离是s),A、B两点到直线l的距离分别是p、q(p≤q),在点A、B和直线l所在平面上求一点F,使点F到A、B两点和直线l的距离之和最小.由于点F在点A、B和直线l所在平面上,先说明一下“Y”字形铺设时点F在什么范围内时FG+FA+FB最小?

①如图8,过点A作AE//l交BC于点E,若点F在AE上或AE的正上方,易证FG+FA+FB≥DA+AB(点F与点A重合时取“=”),若点F在AE左上方或右上方时,同理可证.

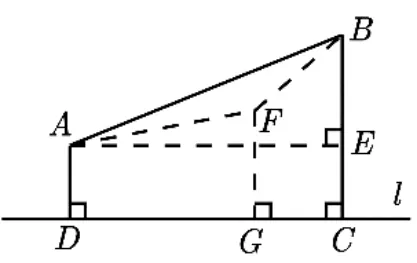
图8

②如图9,若点F在AD左侧过点F作FE//l交AD于点M、BC于点E,易得FA ＞MA,FB ＞MB,MB ＞AB,∴FG+FA+FB ＞DM+MA+MB ＞AD+AB,点F在BC的右侧时,同理可证.

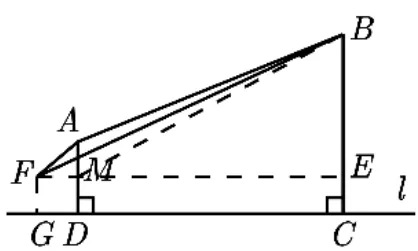
图9

③如图10,当点F在AD或BC上时,易证明FG+FA+FB ＞DA+AB.

图10

综上所述,要使FG+FA+FB最小,点F必在矩形区域ADCE上.

怎样在矩形区域ACDE上确定点F的位置? 如图11,点F是矩形区域ACDE上的一点,过点F作l′//l,FG⊥l于点G,点A′是点A关于直线l′的对称点,连接A′B与l′的交点即为点F,即FG+FA+FB和的值最小时,点A′、F、B三点共线,理由如下:

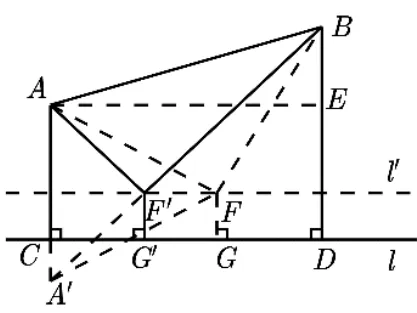
图11

若点F不在直线A′B上时,设A′B交l′于点F′,则FA+FB ＞A′B=F′A+F′B,FG=F′G′,∴FA+FB+FG ＞F′A+F′B+F′G′,这与FA+FB+FG取得最小值矛盾,因此FG+FA+FB最小时,点A′、F、B三点共线.因此只要确定了点F到直线l的距离,就可以利用“轴对称”确定点F的位置.

4 建模解题

如图12,过点F作l′//l,分 别 交AC、BD于点M、N,作FG⊥l于点G,点A′是 点A关 于 直线l′的对称点,过点A′作A′H⊥BD交BD的延长线于点H,取AB的中点P,连 接PM,则PM=A′B,设FG=MC=x,y=FG+FA+FB,易得AM=A′M=p-x,则

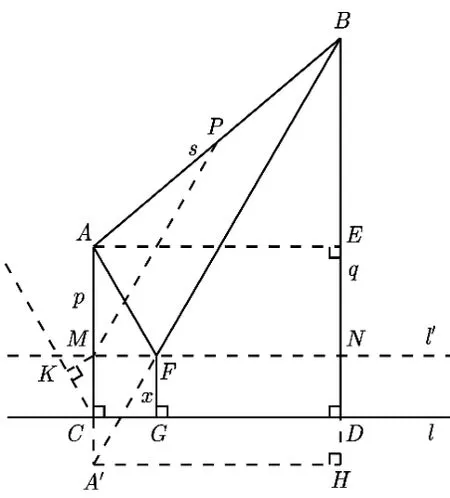
图12

图13

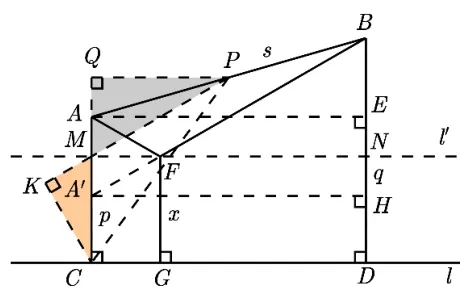
图14

如图15,直线l′与l重合,点G在点A关于l的对称点A′与B点的连线与l的交点处,此时点F与点G重合.

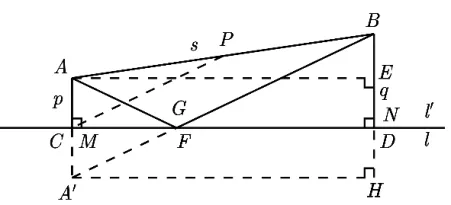
图15

综上所述,可得如下结论.

当∠BAC≥120°,q-p ＜s≤2(q-p)时,点G在直线l上,且与AC的垂足C重合,点F与点A重合,点F到A、B两点和直线l的距离之和最小值是L厂=s+p.

5 一点发现

如图16,当FG+FA+FB最小时,延长PK交直线l于点R.易得∠PMN=∠PRC=∠MFA′=∠FA′H=∠AFM=30°,即直线PR(BA′) 与直线l、l′相交的夹角为30°,∴∠BFN=30°,∴∠AFB=∠AFG=∠BFG=120°,∴点F是ΔAGB的费马点.

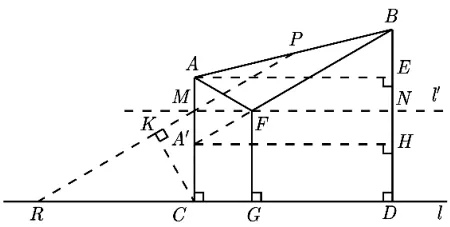
图16

易得,当点F与点A重合或点F在直线l上(点F与点G重合) 时,点F也是ΔAGB的费马点.这是因为费马点可能在三角形内,也可能是三角形的顶点,如果三角形的每个内角都小于120°,在三角形内就存在一点F,使∠GFA=∠GFB=∠AFB=120°,点F就是费马点;如果三角形的某个内角大于或等于120°,这个角的顶点就是费马点.

那么,有没有快速确定点G的简便方法呢? 根据上面的探究容易得到: 分别过A、B两点相对作与直线l的交角为30°的两条直线,设两直线交点为F.若交点F在AB与直线l之间,则过交点F作的直线l垂线,垂足就是点G;若交点F在点A的上方,则过点A作直线l的垂线,垂足就是点G;若交点在直线l的下方,则过点A作直线l的对称点A′,联结A′B与直线l的交点就是点G.如图17 所示.

图17

6 解决问题

现用上面探究的结论解决前面的问题.