错题驱动质疑 立意促进发展
缪晓菊
(南通市如东县茗海中学,江苏 南通)
在初中数学教学过程中,教师如何结合课堂内容、学生的心理状况、教学内容,适时地提出精心设计的问题,培养学生的质疑能力。笔者认为教师如果借助错题的纠错过程,让学生主动发现问题存在的原因,主动地解决问题,对提高课堂教学效率,增强课堂教学活力,培养学生数学核心素养不失为一种好方法。
一、开展错题专项复习,创造质疑环境
如果可以把质疑引入课堂中,教师就需要更新教学观念,让学生因趣生疑,尤其是对错题进行专项复习时,让学生用旧知识解决新问题,使学生因趣生疑、因疑生奇,更好地对错题内容进行深度探究。
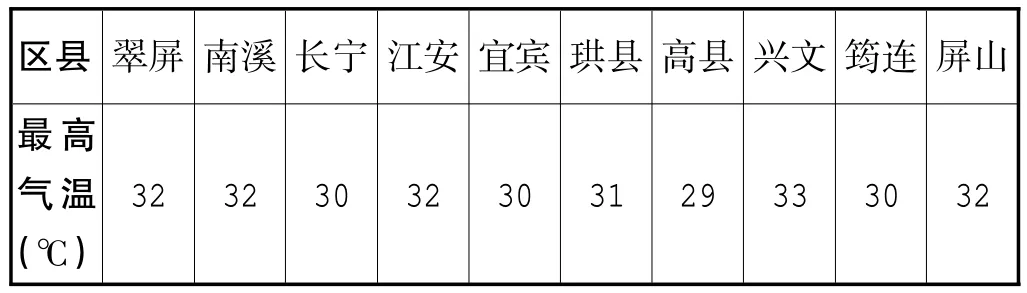
区县 翠屏南溪长宁江安宜宾珙县高县兴文筠连屏山最高气温(℃)32 32 30 32 30 31 29 33 30 32
例如,在对“统计初步”相关知识点的讲解中,首先,针对学生的错误之处,教师需要整理相关的概念,让学生复习与统计初步有关的概念,然后,教师需要出一道例题:宜宾今年5 月某天各区县的最高气温如上表,这道题的中位数是多少?这道题看似简单,但学生屡做屡有错,就需要学生有质疑精神:错因何在?定义理解不深。在这一组数据中32 是出现次数最多的,故众数是32,按大小排列后,处于这组数据中间位置的数是31、32,那么由中位数的定义可知,这组数据的中位数是31.5。
二、总结知识错题内容,探寻错误的疑点处
教师应注重质疑的言传身教性,尤其是对某一知识进行专项总结时,需要让学生明确在哪里找疑点,这个错误是从哪里出发的。有的时候错题的出现,就是因为学生对某一个概念或某一个小知识点不熟悉,只有让学生通过逆向思维,对问题产生质疑,才能更好地开展课堂教学,不断地加强现有的教学活力,丰富学生对知识点的认知能力,更好地开展课堂的学习。
例如,在对“一元二次方程”相关知识点的讲解中,首先,教师出一道例题:分式方程的解为多少?针对这道题,学生就需要运用相关知识点,对方程的两边同乘(x+3)(x-3),得 12-2(x+3)=x-3,解得:x=3。这时,学生要发扬质疑精神,对其进行检验:把x=3代入(x+3)(x-3)=0,即 x=3 不是原分式方程的解,所以原方程无解。然后,教师再总结相关的知识点:一元二次方程对于方程:ax2+bx+c=0:①求根公式 x=是,其中Δ=b2-4ac 叫作根的判别式。当Δ>0 时,方程有两个不相等的实数根;当Δ=0 时,方程有两个相等的实数根;当Δ<0 时,方程没有实数根,注意:当Δ≥0 时,方程有实数根。②若方程有两个实数根x1和 x2,并且二次三项式 ax2+bx+c 可分解为 a(x-x1)(xx2)。
三、发挥错题的主导作用,提高学生的质疑能力
为了更好地让学生对知识点进行探究,教师就需要通过一系列的教学手段,帮助学生养成记错题的好习惯,让学生认识到错题对于复习旧知识的重要程度,让错题占据复习的主导地位,进一步提高学生的质疑能力,更好地对知识点展开探究。
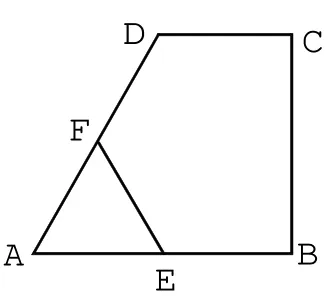
例如,在对“立体几何”相关知识点的讲解中,首先,针对学生的学习情况,教师需要出一道学生易错的题,如图,在四边形 ABCD 中,DC∥AB,分别为AB,AD 的中点,则△AEF 与多边形BCDFE 的面积之比为多少?针对这道题,需要学生过D 作DM⊥AB 于 M,过 F 作 FN⊥AB 于 N,即 FN∥DM,F 为 AD 中点,N 是 AM 中点,DM⊥AB,CB⊥AB,DM∥BC,DC∥AB,四边形 DCBM 是平行四边形,DC=BM,BC=DM,AB=ADAB,点 E,F 分别为 AB,AD 的中点,设 DC=a,AE=BE=b,则 AD=AB=2a,BC=DM=2a,,所以△AEF 的面积是,多边形 BCDFE 的面积是,所以△AEF 与多边形BCDFE 的面积之比为然后,教师让学生继续复习相关的知识点,对几何图形公式进行总结,如三角形的内心与外心,在理解概念的基础上,要让学生比较异同,理解一些常见结论。(1)Rt△ABC的三条边分别为:a、b、c(c 为斜边),则它的内切圆的半径;(2)△ABC 的面积和周长分别为 S、C,则它的内切圆的半径
总体来说,初中数学教师就需要强化学生的质疑能力,努力实现学生知识水平与教材的相融合,让学生带着疑问去听课、去复习错题,对新的知识点产生新的质疑,对错题产生自己的思考方式,才能不断地加强现有的教学效果,学生学习数学和应用数学解决问题的能力才能得以发展。

