三角恒等变换中的“一题多解”
2022-02-13 10:42:38田玉帅
中学生数理化·高一版 2022年1期
■田玉帅

一题多解能开拓思路、发展智力、培养发散思维,能提高分析问题和解决问题的能力,通过对问题进行多角度、多层次分析,达到对问题的全面理解,将有助于提高解题的速度和质量。下面举例分析。

感悟:本题考查三角函数的恒等变换与化简求值。解决三角函数求值问题的关键是把“所求角”用“已知角”表示。当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;当“已知角”有一个时,应着眼于“所求角”与“已知角”的和、差或倍半的关系。万能公式是沟通二倍角的正弦、余弦及正切的桥梁。
例2(2021 年全国新高考卷改编)若tanθ=-2,则=____。
解法1:先利用二倍角公式和平方关系配方化简,然后增添分母(1=sin2θ+cos2θ)化为正切的表达式可得结果。
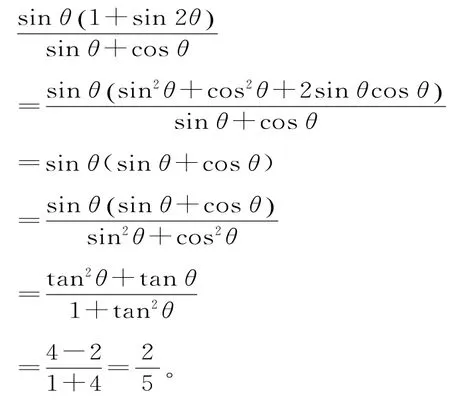
解法2:利用已知条件,借助sin2θ+cos2θ=1求解。因为tanθ==-2,所以sinθ=-2cosθ。
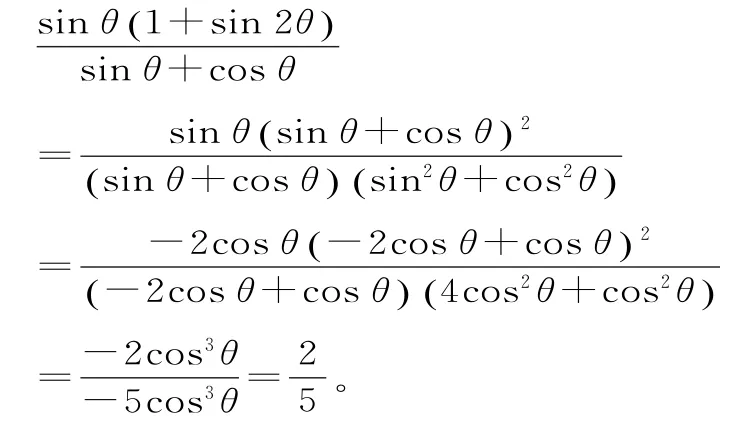
感悟:若利用tanθ=-2,求出sinθ,cosθ的值,还需要分象限讨论其正负,其解法烦琐。通过分子、分母同除以cosα,得到关于tanα的式子,再求值,其解法简单明了。有时灵活地进行“1”的代换(1=sin2α+cos2α),是三角化简与求值的常用方法。
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04 06:20:50
读写月报(初中版)(2021年12期)2021-05-25 13:23:18
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:54
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
未来英才(2016年18期)2017-01-05 13:37:26
新教育时代·教师版(2016年27期)2016-12-06 17:12:13
高中生·天天向上(2016年7期)2016-11-22 10:56:56
考试周刊(2016年78期)2016-10-12 13:13:51
黄河之声(2016年24期)2016-02-03 09:01:52

