TC4钛合金疲劳寿命不确定度评定

李 凯, 卢 奇, 郑 程, 巴发海

(上海材料研究所 上海市工程材料应用与评价重点实验室, 上海 200437)

在实际测量过程中，测量值是包含测量过程中的随机效应以及系统效应引入不确定度真值的估计值。不确定度表征了测量结果的可靠程度，是量值溯源体系中不可缺少的一部分。JJF 1059.1—2012 《测量不确定度评定与表示》与ISO/IEC GUIDE 98-3:2008 《测量的不确定性 第3部分：测量不确定性的表达指南》中的内容是不确定度评定最常用和最基本的方法，也称为GUM法。GUM法评定不确定度的主要步骤包括：不确定度来源分析、测量模型建立、标准不确定度计算、合成不确定度计算、扩展不确定度计算以及结果表示等[1]。

在计量校准领域，依据GUM法评定不确定度已经得到广泛应用，CNAS-CL01：2018 《检测和校准实验室能力认可准则》第7.8.4.1条款中规定校准报告必须包含校准结果的不确定度。随着行业的发展，检测领域也越来越重视不确定度的评定，GB/T 228.1—2021 《金属材料 拉伸试验 第1部分：室温试验方法》对拉伸试验中抗拉强度、断后伸长率等性能的不确定度评定进行了详细介绍。对于疲劳试验，仅有GB/T 24176—2009 《金属材料 疲劳试验 数据统计方案与分析方法》给出了升降法测量疲劳强度结果标准偏差的计算方法。疲劳寿命不确定度评定也引起了行业专家的重视，并取得了一些研究成果。冉学臣[2]在假设对数疲劳寿命服从正态分布的前提下，得出45钢旋转弯曲疲劳对数寿命扩展不确定度为0.19～0.20。高怡斐等[3]对GB/T 24176—2009中的数据进行了深入分析和计算，得出对数疲劳寿命扩展不确定度为0.09～0.11。总体来说,由于影响疲劳寿命的因素多且复杂，因此尚未形成疲劳寿命不确定度的统一评定方法。笔者以TC4钛合金为例，给出了一种通用的疲劳寿命不确定度的评定模型与实例，数据正态性检验、异常值判定等关键步骤使得不确定度评定过程更为严谨与完善。

1 试验方法

试验材料为TC4钛合金棒材。采用光电直读光谱仪进行化学成分分析，根据GB/T 228.1—2021，用电子万能试验机进行拉伸试验，试样数量为3支，拉伸速率为1 mm/min。根据GB/T 3075—2021 《金属材料 疲劳试验 轴向力控制方法》，采用高频疲劳试验机进行疲劳试验，试样数量为10支，轴向加载，波形为正弦波，应力比为0.1，最大应力为700 MPa，试验频率由试验系统的共振频率确定。拉伸试验与疲劳试验的试样结构如图1所示。

图1 拉伸试验与疲劳试验的试样结构示意

2 试验结果

TC4钛合金的化学成分分析结果如表1所示，结果符合GB/T 2965—2007 《钛及钛合金棒材》对TC4钛合金棒材成分的规定。TC4钛合金试样抗拉强度测试结果如表2所示，试样抗拉强度的平均值为1 079 MPa，试样的疲劳寿命测试结果如表3所示。

表1 TC4钛合金的化学成分分析结果 %

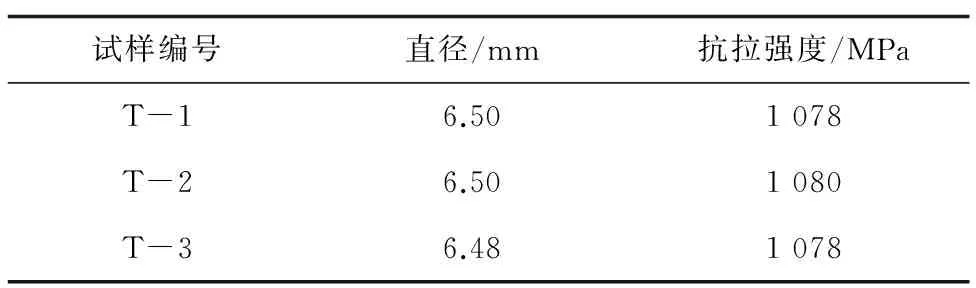
表2 TC4钛合金试样的抗拉强度测试结果

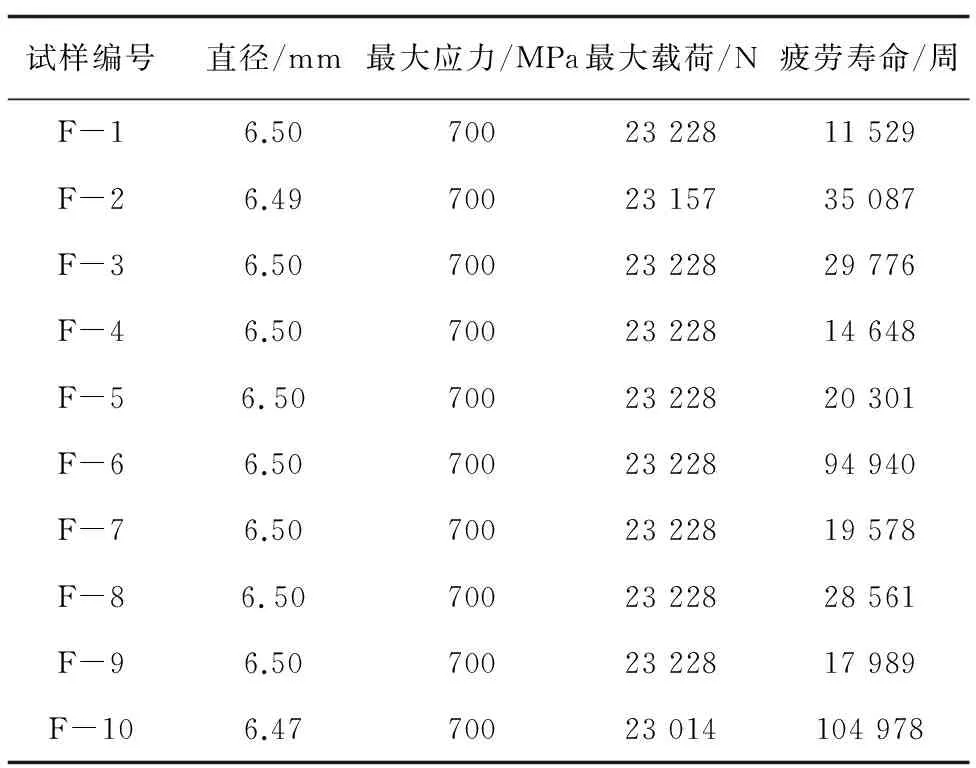
表3 TC4钛合金试样的疲劳寿命测试结果

2.1 正态性检验

通常指定应力下的疲劳寿命或对数疲劳寿命服从正态分布，不确定度评定以及奇异值判定都需要明确其分布规律，参照GB/T 4882—2001 《数据的统计处理和解释 正态性检验》进行正态性检验。Shapiro-Wilk检验适用于样本数量8≤n≤50的正态检验。Shapiro-Wilk检验为一个完全样本方差分析形式的检验。检验统计量为样本次序统计量线性组合的平方。Shapiro-Wilk检验步骤如下所述。

零假设：样本的总体数据服从正态分布。

将n个独立观测值按非降序记为x1,x2,x3,…，xn，然后计算Shapiro-Wilk检验的辅助量S，如式(1)所示。

S=∑ak[xn+1-k-xk]

(1)

式中:当n为奇数时，下标k为1,2,…,(n-1)/2；当n为偶数时，下标k为1,2,…,n/2;ak为与样本量n相关的特定值，可以查表得到。

检验统计量W的计算方法如式(2)所示。

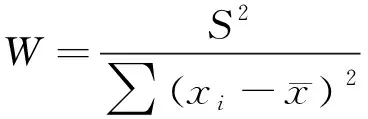
(2)

在显著性水平α=p下，如果W小于其p分位数(p=α)，则拒绝零假设。TC4钛合金疲劳寿命Shapiro-Wilk检验计算结果如表4所示。

表4 TC4钛合金疲劳寿命Shapiro-Wilk检验计算结果

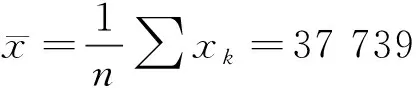
(3)

S=∑ak(xn+1-k-xk)=85 293

(4)

则计算得：W为0.714。

当n=10，且p=α=0.05时,p分位数为0.842，由于计算得到的W小于该值，因此在显著性水平α=0.05上拒绝零假设，即根据Shapiro-Wilk检验，疲劳寿命不服从正态分布。按同样方法对对数疲劳寿命进行Shapiro-Wilk检验。

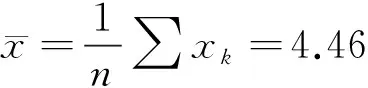
(5)

S=∑ak(xn+1-k-xk)=0.908

(6)

W>W(n=10,α=0.05)

(7)

根据Shapiro-Wilk检验，对数疲劳寿命服从正态分布。

2.2 异常值判定

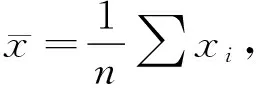
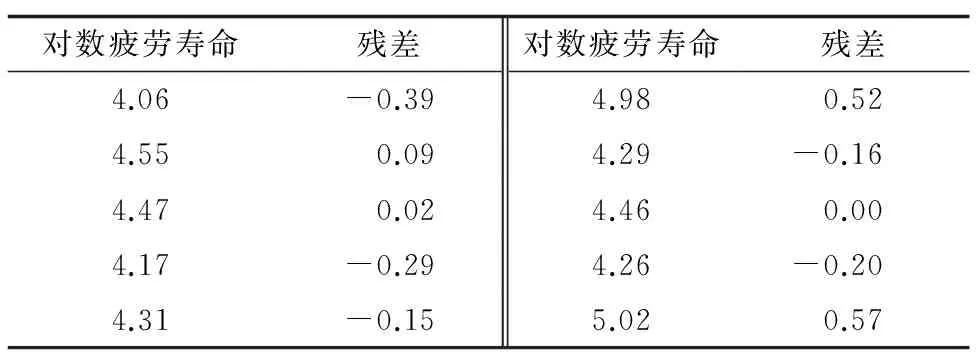
表5 TC4钛合金对数疲劳寿命异常值判定

表5中绝对值最大的残差v=0.57，相应的对数疲劳寿命5.02为可疑值，则

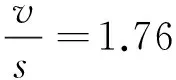
(8)

按照p=0.95，α=0.05，n=6时，格拉布斯临界值G(0.05,10)=2.176，则

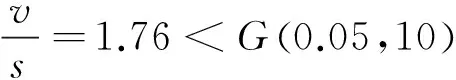
(9)

3 不确定度评定

3.1 不确定度来源分析

疲劳试验属于破坏性试验，疲劳寿命不确定度评定不描述由材料不均匀性引起的分散，不确定度来源于从理想均质材料中提取的不同试验、不同试验机、不同实验室获得的数据分散性。从仪器、环境、人员、方法等方面考虑，不确定度来源主要有测量重复性引入的不确定度分量u1、试验机力值引入的不确定度分量u2、试样尺寸测量引入的不确定度分量u3等3部分。

3.2 数学模型

试验机循环次数N为输入量，对数疲劳寿命lgNf为输出量。因此建立数学模型如式(10)所示。

lgNf=lgN

(10)

式中：Nf为疲劳寿命；N为试验机循环次数。

式(3)中没有直接体现出试验机力值、试样直径测量等不确定度来源分量。对于实际进行试验后的疲劳试样，其疲劳寿命直接通过试验机记录循环次数得到，这个计数本身是准确的，无需评定不确定度。疲劳寿命的定义是：在指定的应力水平下，试样失效之前经历的循环次数。因此疲劳强度不确定度评定过程中的输入量是应力水平、试样尺寸等参数，输出量是疲劳寿命。对数疲劳寿命与应力水平可以按照线性模型分析。

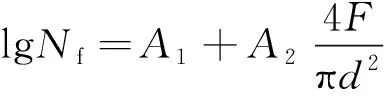
(11)

式中：F为试验力；d为试样直径;A1,A2均为待定系数。

对于不同的材料、试样形状、加载水平，式(11)中的待定系数A1,A2均不同。当疲劳试验中最大应力水平为材料抗拉强度时，对数疲劳寿命lgNf=0。即疲劳试验中最大应力为抗拉强度1 079 MPa时，对应的TC4钛合金的对数疲劳寿命lgNf=0。通过表 3中的试验数据可知，最大应力为700 MPa时，对数疲劳寿命平均值为4.46，则将(1 079,0)，(700,4.46)分别代入式(11)可得

(12)

解方程组可得

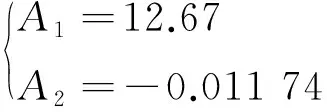
(13)

最终数学模型为

(14)

也可以通过多应力水平下疲劳寿命对待定系数进行求解。

3.3 灵敏系数

灵敏系数c1,c2,c3为模型中各个不确定度分量的偏导数,具体为

(15)

试样直径d=6.5 mm，试验应力为700 MPa，试验力F=23 228 N，代入式(15)可得

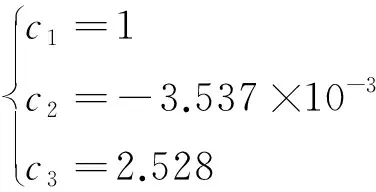
(16)

3.4 不确定度分量

3.4.1 测量重复性引入的不确定度分量u1

测量重复性引入不确定度分量按照A类标准不确定度进行评定。10次测量的标准偏差按照贝塞尔式计算。

(17)

通常在指定应力水平下测试疲劳寿命时，会进行3次测量，因此测量重复性引入的不确定度分量u1=0.185 4。

A类评定的标准不确定度的自由度ν1=9。

3.4.2 试验机力值引入的不确定度分量

B类评定的标准不确定度的自由度为

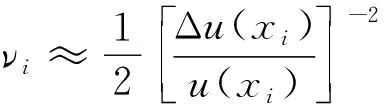
(18)

3.4.3 试样尺寸测量引入不确定度分量

试样尺寸测量应精确到0.5%，试样工作段直径为6.5 mm，最大允许误差为±0.032 5 mm，按照B类不确定度评定，半宽区间a=0.032 5 mm，按正态分布，k=2，则试样尺寸测量引入不确定度分量u3=0.016 25 mm。

由试验机力值引入的不确定度分量的自由度可得，试样尺寸测量引入不确定度分量的自由度ν3=8。

3.5 合成标准不确定度uc

测量重复性引入的不确定度分量u1、试验机力值引入的不确定度分量u2、试样尺寸测量引入的不确定度分量u3互不相关，由不确定度传播率可得合成标准不确定度为

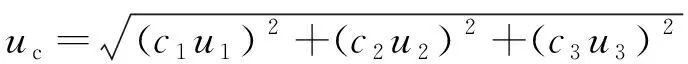
(19)

式中：u1,u2,u3为各分量标准不确定度。

各不确定度分量如表6所示。

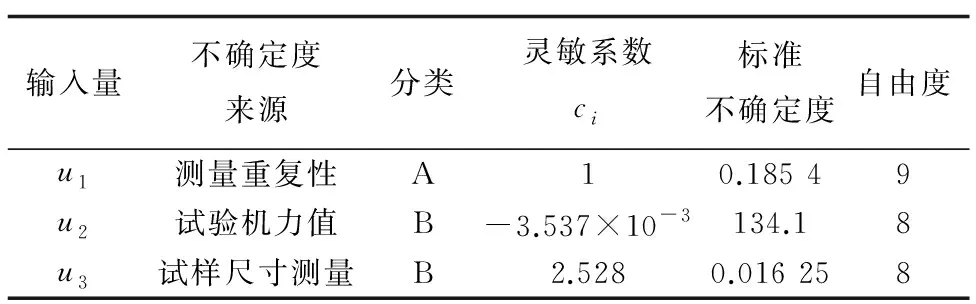
表6 各不确定度分量汇总

将表6中的数据代入式(22)可得标准不确定度uc=0.20。

当各分量间相互独立，且输出量接近正态分布或t分布时，合成标准不确定度的有效自由度为

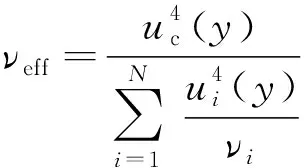
(20)

将表6中数据代入式(23)，可得νeff=11。

3.6 扩展标准不确定度

对数疲劳寿命服从正态分布，取包含因子k=2，扩展标准不确定度U=0.40。

对数疲劳寿命的扩展不确定度U=0.40。

4 结论

(1) TC4钛合金在应力比R=0.1,最大应力为700 MPa，正弦波、轴向加载试验条件下的疲劳寿命lgNf=4.46,U=0.40，有效自由度νeff=11。

(2) 疲劳寿命测量不确定度的来源主要有：测量重复性、试验机力值以及试样尺寸测量。

(3) 疲劳寿命不确定度评定模型中，疲劳寿命与应力之间的关系可以采用线性模型。

(4) 评定不确定度之前，需要进行异常值判定以及正态分布验证。