基于多电磁无损检测的管线钢硬度检测模型

杜裕平

(1.南京钢铁股份有限公司, 南京 210035； 2.南京航空航天大学 自动化学院, 南京 200240)

硬斑是钢板上的一种缺陷，指钢板表面局部区域的硬度异常高于其他正常部位的硬度，这些区域可能是成分异常区、外来杂质或者过冷区等。这些硬斑区域附近存在很大的硬度差，材料在塑性变形或者服役过程中，可能产生应力集中，导致表面产生裂纹，严重影响管道的服役安全。

基于铁磁性材料微观结构的微磁无损检测技术，可以直接提取反映材料微观结构的电磁信号，同时材料微观结构决定材料的宏观硬度[1]。国内外学者在多电磁检测技术方面进行了研究，中国矿业大学范孟豹科研团队融合涡流、巴克豪森(MBN)两种检测技术，采用BP(Back Propagation)神经网络模型，实现了轴承套的表面硬度检测[2]。北京工业大学何存富科研团队融合切向磁场谐波分析和巴克豪森检测技术，采用多元回归模型，完成了对12CrMoV钢板表面硬度的预测[3]。德国弗朗霍夫研究所研发的3MA综合无损检测技术，集成了巴克豪森、增量磁导率、多频涡流、切线磁场谐波分析等多项微磁无损检测技术，采用多元回归模型，对铁磁性材料的硬度、强度等进行检测[4]。

笔者基于3MA设备提取了41个特征值，分析了特征参数与管线钢表面硬度的关系，并构建了逐步回归和BP神经网络模型，以对管线钢的表面硬度进行检测。

1 试验方法

1.1 试验设备

采用德国3MA设备(见图1)获取电磁特征参数，其探头结构如图2所示(图2中，1为保护壳，2为探头电子元件，3为磁轭，4为轭线圈，5为探头电缆，6为弹簧加载传感器元件，7为磁场传感器，8为电感式传感器，9为检测试样)。

图1 3MA设备外观

图2 3MA设备探头结构示意

巴克豪森信号由位于试样表面上的磁感应传感器接收，并使用带通滤波器或低通与高通滤波器的组合对检测到的信号进行滤波并放大。此后，还需要对信号进行整流，包括放大和信号平滑等过程。与MBN信号类似，增量磁导率(MIP)检测技术也提取类似特征。

切向磁场谐波分析技术是在电压驱动磁化的情况下，将频率为fM的正弦激励电压施加到电磁铁的磁轭线圈上，根据电磁铁的总电感和材料的磁滞回线形状，探头磁轭线圈中将产生与时间相关的非正弦电流。除了基频fM之外，磁化电流将会出现高次谐波。

3MA设备应用4种不同的涡流频率去激励检测线圈，对检测信号解调处理后，得到每个频率的实部和虚部，以及阻抗的幅度和相位，这样可以使得目标值与干扰因素分离，有利于提高检测精度。

3MA设备采用多元回归方法得到电磁特征与目标的数据模型，但这种算法依赖特征参数与目标的相关性，具有一定的限制性。当参数与目标的相关性较低时，所得结果误差较大。

1.2 试样制备及硬度检测

制备的试样尺寸为750 mm×300 mm×30 mm(长×宽×高)，结构及测点如图3所示。

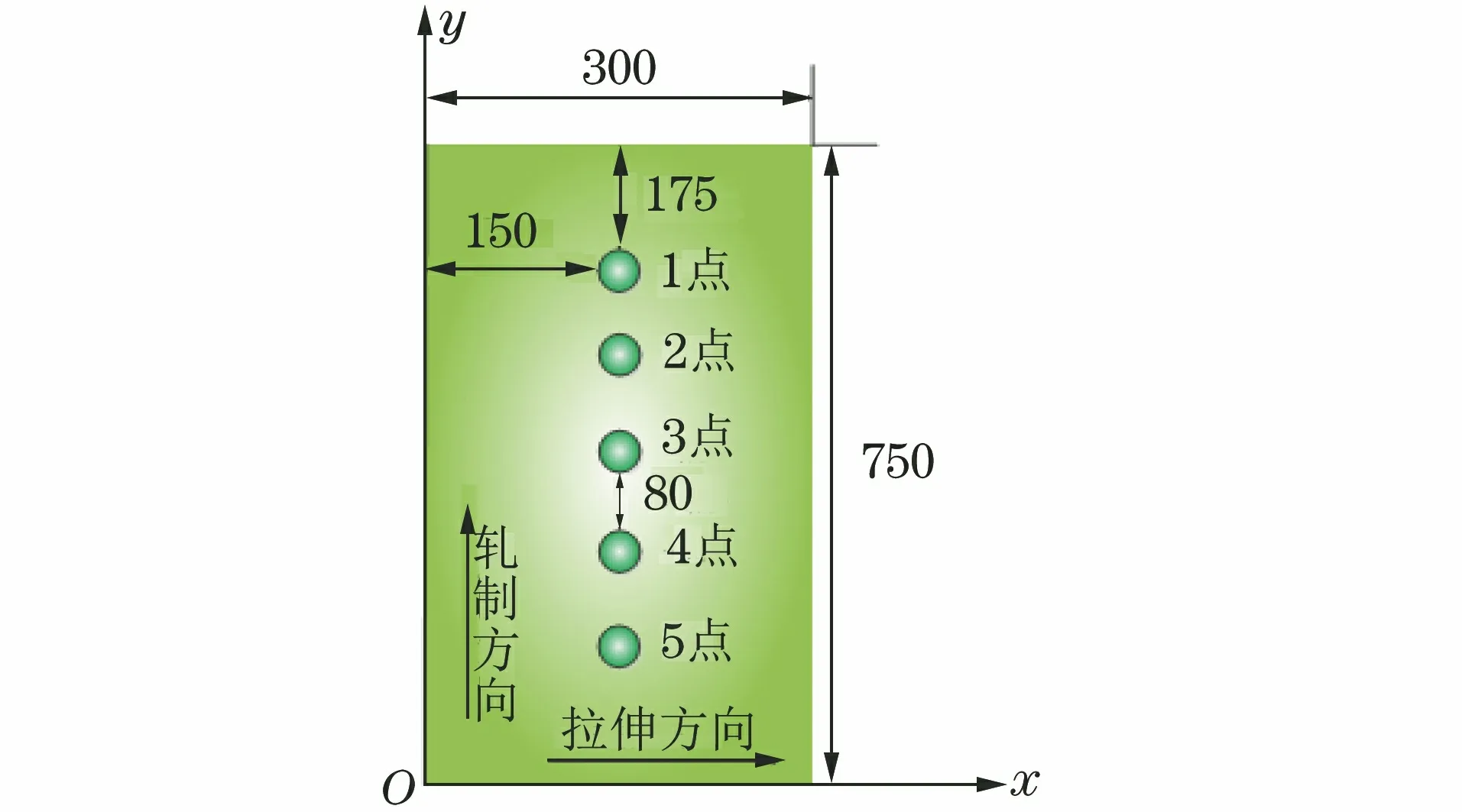
图3 试样结构及测点示意

首先在钢板正面取5个点，探头磁场方向与轧制方向垂直，每个点的采集时间为30 s，提离距离为2 mm。采用里氏硬度计对钢板的表面硬度进行检测，结果如表1所示。

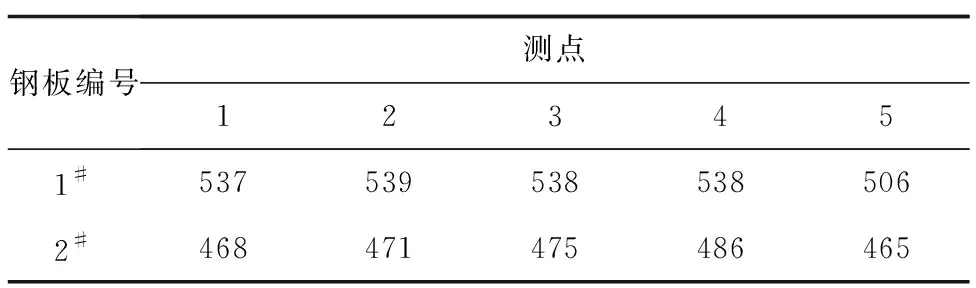
表1 部分试样表面硬度检测结果 HV

1.3 检测模型及评估函数

逐步回归算法是将所有解释变量逐一引入，通过F检验和t检验后确认显著变量，并将不显著变量删除，循环往复得到最优回归方程，用于拟合。3MA检测系统采用的算法是逐步回归算法，但在实际应用中，为了保证实时传输和计算，系统只选取10个最优特征值进行回归建模，使得其余31个相关参数被遗弃，导致回归模型跨度大，拟合精度低。

文中采用的逐步回归算法模型并不依赖于3MA检测系统，而是编写的算法。该算法模型将41个参数包括在内，建立了回归方程，进一步提升了拟合的精度。逐步回归算法流程如图4所示。

图4 逐步回归算法流程图

人工神经网络(ANN)是模拟生物大脑神经系统建立的一种数学模型，具有很强的信息处理和自学习能力，能有效识别复杂系统输入向量和输出向量之间的非线性映射关系，特别适用于解决输出受较多输入因素影响，且影响关系不明确的建模问题。根据不同的学习特性和功能，ANN可分为BP神经网络、径向基神经网络、线性神经网络、自组织神经网络等，其中BP神经网络是目前应用最广泛的一种ANN模型。

网络结构由输入层、隐含层、输出层3部分构成，其中输入层和输出层各只有1个，而隐含层可以有多个，各层都由若干神经元组成。层内神经元节点之间互不相连，而层间神经元节点采用全连接的方式，即输入层的任意一个神经元节点都与隐含层的所有节点连接，隐含层的任意一个神经元节点都与输出层的所有节点连接。BP学习算法流程如图5所示。

图5 BP学习算法流程图

为了对两种模型预测精度进行进一步分析，可以使用两种模型对同一批管线钢进行强度和硬度预测，根据预测结果来对比两种模型的性能。笔者所用结果的评价指标以置信区间为主。

模型检测误差，即预测结果有一个合适的置信区间，才能保证预测有意义。文中的置信区间有两个，一个是相对误差绝对值不大于10%，另一个是相对误差绝对值不大于5%，置信区间Q10，Q5的计算公式为

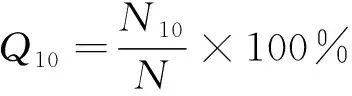
(1)

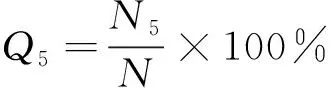
(2)

式中：N为样本的总数；N5为绝对值误差在5%以内的测试样本个数；N10为绝对值误差在10%以内的测试样本个数。

绝对误差为

(3)

式中:yi为力学性能参数;yci为力学性能参数检测结果。

2 试验结果及分析

2.1 微磁特征信号与表面硬度的关系

3种特征的矫顽力与钢板硬度的关系如图6～8所示。由图6～8可知，1#，2#钢板的硬度分布存在差异，即便是同类管线钢，不同批次间的硬度也存在差异。同时随着钢板硬度的增加，3种特征的矫顽力呈现增大趋势，表明3种微磁检测技术所提取的特征值可在一定程度上反映管线钢的硬度。

图6 矫顽力与钢板硬度的关系(巴克豪森特征)

图7 矫顽力与钢板硬度的关系(切向磁场特征)

图8 矫顽力与钢板硬度的关系(增量磁导率特征)

2.2 表面硬度检测结果

对L450M钢进行硬度检测和计算，结果如表2所示。

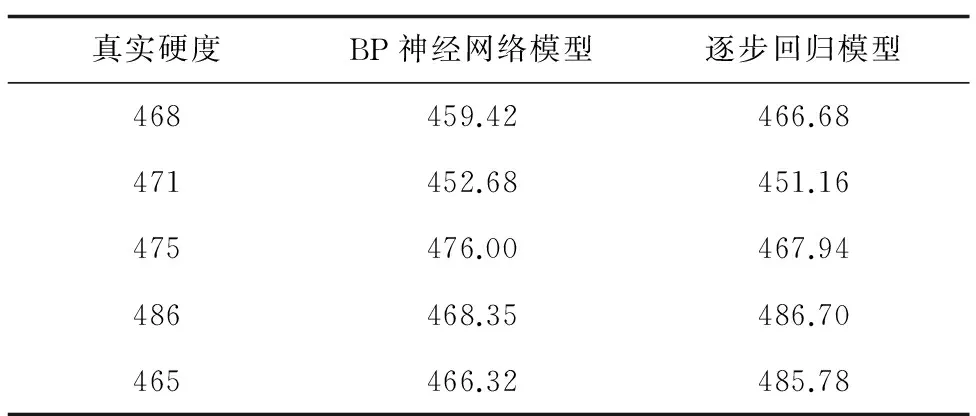
表2 L450M钢硬度检测和计算结果 HV

L450M钢BP神经网络模型和逐步回归模型检测结果如图9，10所示。对L450M钢进行BP神经网络及逐步回归两种算法的检测结果为：在5%和10%的误差范围内，置信度都为100%。

图9 L450M钢BP神经网络模型检测结果

图10 L450M钢逐步回归模型检测结果

对L485钢进行硬度检测和计算，如果如表3所示。

表3 L485钢硬度检测和计算结果 HL

L485钢BP神经网络模型和逐步回归模型检测结果如图11，12所示。对L485钢进行逐步回归算法检测结果为，在5%和10%的误差范围内，置信度都为100%；BP神经网络算法检测结果为，在5%的误差范围内，置信度为92.24%;在10%的误差范围内，置信度为100%。

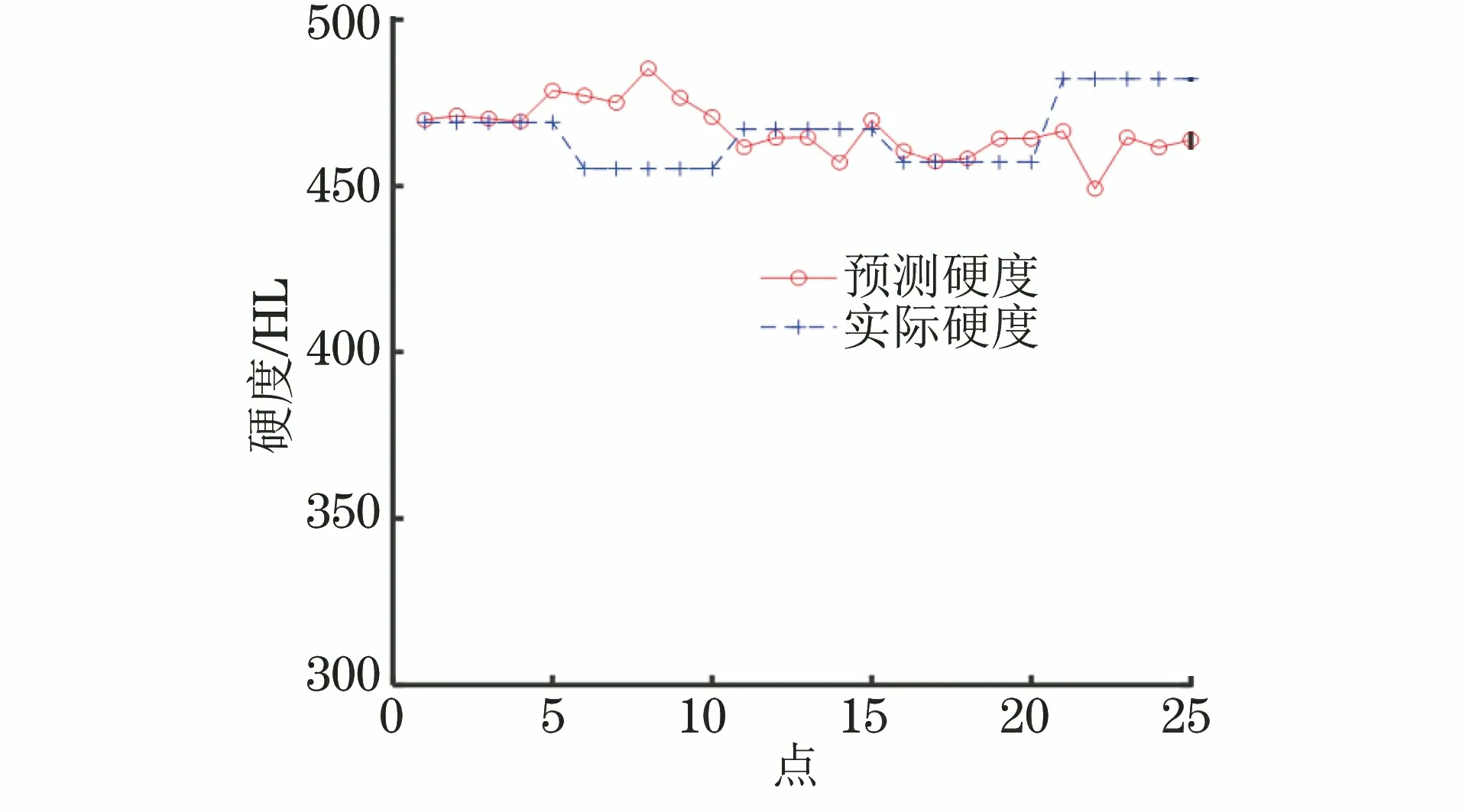
图11 L485钢BP神经网络模型检测结果

图12 L485钢逐步回归模型检测结果

3 结论

(1) 随着钢板硬度的增加，3种特征值呈现增大趋势，表明3种微磁检测技术提取的特征值可在一定程度上反映管线钢的表面硬度。

(2) 无论是BP神经网络模型还是逐步回归模型，在10%的误差范围内，置信度为100%。表明两种检测模型均可实现对管线钢表面硬度的检测。