结构动态监测信号缺失数据的LSTM和ARIMA预测对比研究

王校昌，王大鹏

（苏州科技大学 土木工程学院，江苏 苏州 215011）

传感器监测数据丢失或者损坏，是结构健康监测（Structural Health Monitoring，SHM）系统的常见情况。此时，需要对缺失数据进行恢复或预测，通常采用的方法分为基于模型的方法和数据驱动的方法。倪一清等[1]对一个600 m超高层建筑在强台风作用下的风压测试数据，应用BP神经网络（Back Propagation Neural Network，BPNN）和广义回归神经网络（Generalized Regression Neural Network，GRNN）两种方法，进行了缺失数据的重构。结果表明，采用贝叶斯（Bayesian）正则化技术来提高BP神经网络的泛化能力，效果更好。

Yang等[2]利用最小化稀疏恢复和核范数最小化低秩矩阵，来恢复随机缺失或损坏的结构振动响应数据。鲍跃全等[3]提出了基于压缩采样恢复缺失数据的方法，通过分析无线传感器在斜拉桥和空间结构上获得的加速度时程数据，进行了验证。鲍跃全等[4]提出了压缩感知恢复缺失数据的方法，利用快速无线传感技术在斜拉桥上获得的现场试验数据，验证了方法的可行性。陈智成等[5]提出了一种从基于对数分位数密度-再生核希尔伯特空间分布到分布回归方法，用于恢复健康监测缺失数据的概率分布，结果表明优于传统方法。彭勇等[6]基于经验模态分析EMD（Empirical Mode Decomposition，EMD）和门控循环GRU（Gated Recurrent Unit，GRU）神经网络来预测高速公路行程时间，取得较好的效果。Mei等[7]使用长短时记忆网络（Long Short-Term Memory，LSTM）和贝叶斯融合对实时移动带宽进行了预测，实现了较高精度地实时预测。唐鸣等[8]建立了三层LSTM来预测水位，与深度神经网络（Deep Neural Networks,DNN）模型预测的结果进行对比发现，LSTM的预测结果较好。

本文拟建立LSTM模型和差分整合移动平均自回归模型（Autoregressive Integrated Moving Average Model，ARIMA），针对结构健康监测常用的FBG（Fiber Bragg Grating，FBG）传感器和加速度计实测振动信号，对比研究两种方法用于动态监测信号缺失数据的预测效果。

1 时间序列预测方法

1.1 长短期记忆网络（LSTM）

LSTM是循环神经网络（Recurrent Neural Network，RNN）的变体，克服了梯度消失和梯度爆炸的问题，其内部结构如图1所示。LSTM有两个传输状态：ct（cell state）和ht（hidden state）。所用激活函数为tanh和sigmoid，输出值为0和1之间，公式分别如下式（1）与式（2）所示。

图1 LSTM内部结构

LSTM提供了三个门，输入门决定哪些信息保留下来，保留在记忆单元ct；遗忘门决定t时刻应该删除哪些信息；输出门控制单元状态ct有多少输出到当前输出值ht。表述如下。

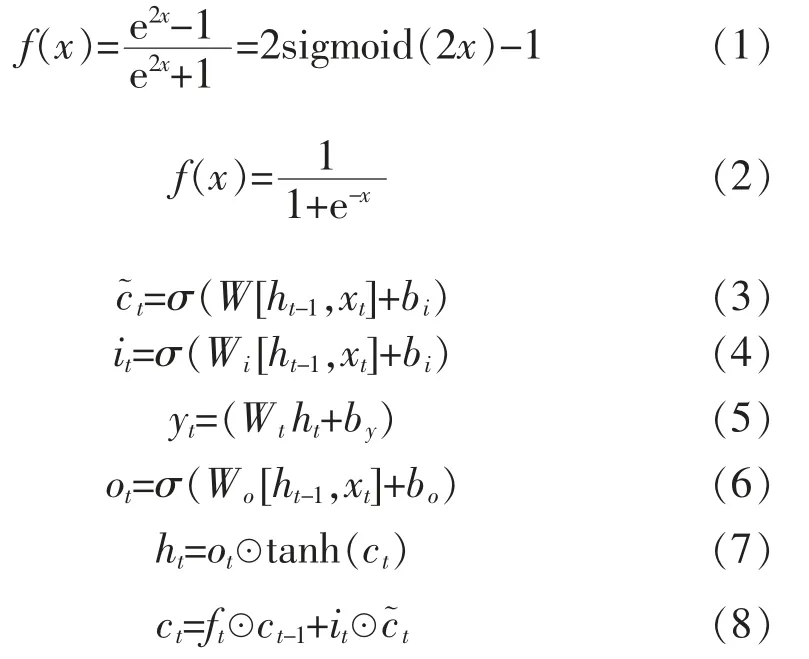
其中，ct、为t时刻的单元状态和更新状态；ht、ht-1为隐藏状态；W为对应的权重；bi为对应的偏差。

1.2 差分整合移动平均自回归模型（ARIMA）

ARIMA（p,d,q)于1970年被提出，被广泛应用于各种时间序列预测中。其中，p是自回归项的阶数，d是差分阶数，q是滞后预测误差的阶数。模型可以写成

2 建模流程

采用编程软件python3.6和pytorch1.5框架进行模型设计，LSTM模型建模流程如图2所示。ARIMA建模过程如图3所示。

图2 LSTM建模流程

图3 ARIMA建模流程

3 试验设计和数据

试验模型为简支工字钢梁，两支点间距为3 m，见图4。钢梁上共安装16个FBG传感器。其中，沿钢梁下翼缘一侧10个FBG标距为300 mm，另一侧6个标距为500 mm，调制解调设备的采样频率为250 Hz。在梁顶放置6个压电式加速度度传感器，动态采集系统的采样频率为100 Hz。使用电磁激振器，采用扫频方式，对钢梁进行2 min激振，得到16组FBG波长数据和6组加速度数据，将数据截取为若干组3 000（采样点数）×q（传感器数量，本文中为6或者16）的数据集，其中90%作为训练集，10%作为测试集。

图4 工字钢梁试验

数据在输入模型进行训练前，按照下式进行标准化的预处理，一组典型标准化数据如图5所示。

图5 标准化数据

4 预测分析过程

4.1 LSTM模型的预测分析

4.1.1 参数选择 LSTM模型为两层，第一层为LSTM，第二层为全连接层。LSTM优化器选择自适应梯度下降算法(Adam)，参数的梯度传入模型由Adam计算，损伤函数选择交叉熵函数。交叉熵公式如下：

式中，J是交叉熵损失函数的值，p和q分别是预期输出和预测输出（概率），M是类别数。

本文针对10组不同超参数，用绝对百分比误差最大值MAX、平均绝对误差MAE及均方根误差RMSE，三项指标（具体见下式（12）至式（15）），比较了超参数对预测效果的影响，如表1所列。由2、3、4、5组可知，迭代次数影响计算效率。4、6、7、8组可以看出，隐含层节点数增加，误差减小，计算精度上升。1、4、9、10组可以看出，模型学习率过小会出现精度不够的现象，学习率过大则出现过拟合现象。

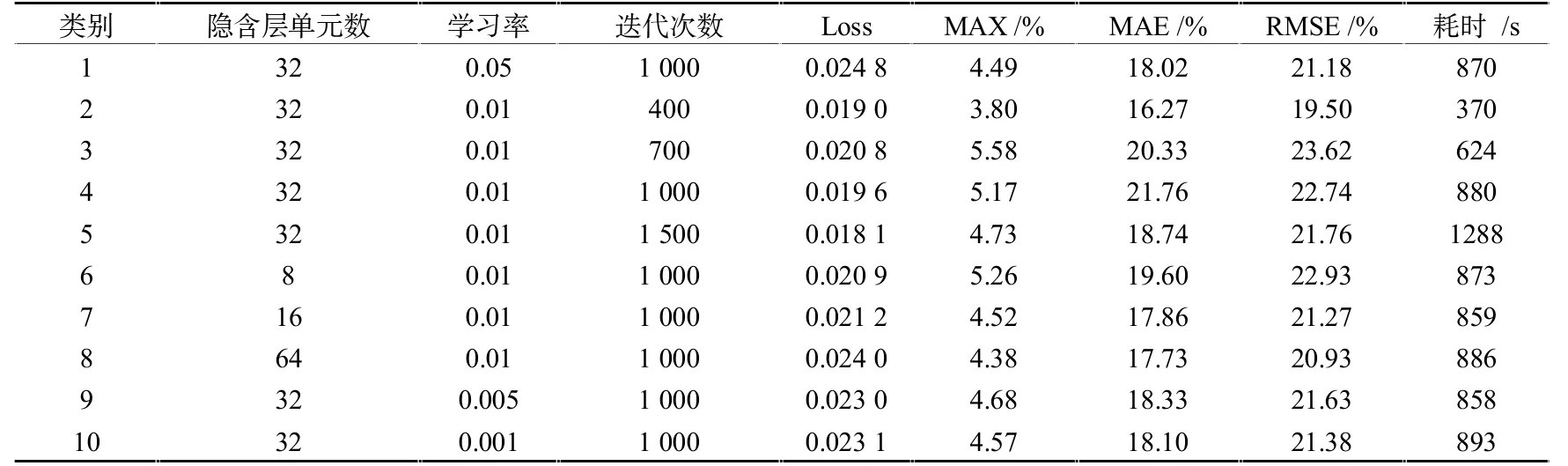
表1 不同超参对预测精度及计算效率的影响

综合考虑计算效率和精度影响，本文LSTM模型的学习率选择为i=0.01、隐含层单元数为h=32、输入节点数n=2、输出节点数o=1，最佳迭代次数为1 000次。

4.1.2 参数选择 LSTM的训练损失变化如图6所示，大概训练100次后，模型损失开始迅速下降。随着训练次数增加，损失值不断下降，直至收敛。图7显示了部分时间序列的波长和加速度数据预测结果。

图6 LSTM模型损失图

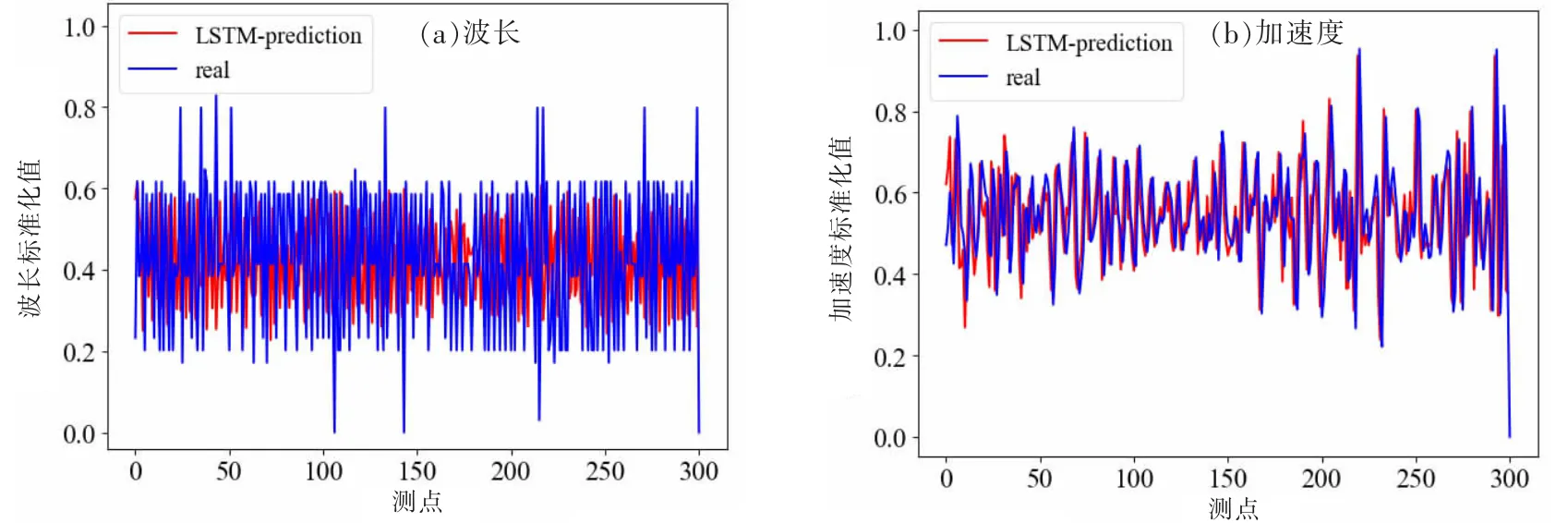
图7 LSTM预测效果图

4.2 ARIMA模型的预测结果

4.2.1 数据平稳性检验 本文ARIMA模型的自回归项阶数p=5，差分阶数d=1，滞后预测误差阶数q=0。采用ADF（Augmented Dickey-Fuller,ADF）单位根检测法进行平稳性检测，得到的显著性检验统计量小于三个置信度（10%、5%和1%）。如表2所示，波长和加速度时间序列的统计量（t-Statistic）分别为-10.528 956和-5.459 338，均小于1%测试临界值-3.432 546和-3.432 552，因此两种时间序列数据满足平稳性要求。

表2 ADF检验

4.2.2 预测结果 图8显示了部分时间序列的波长和加速度数据预测结果。

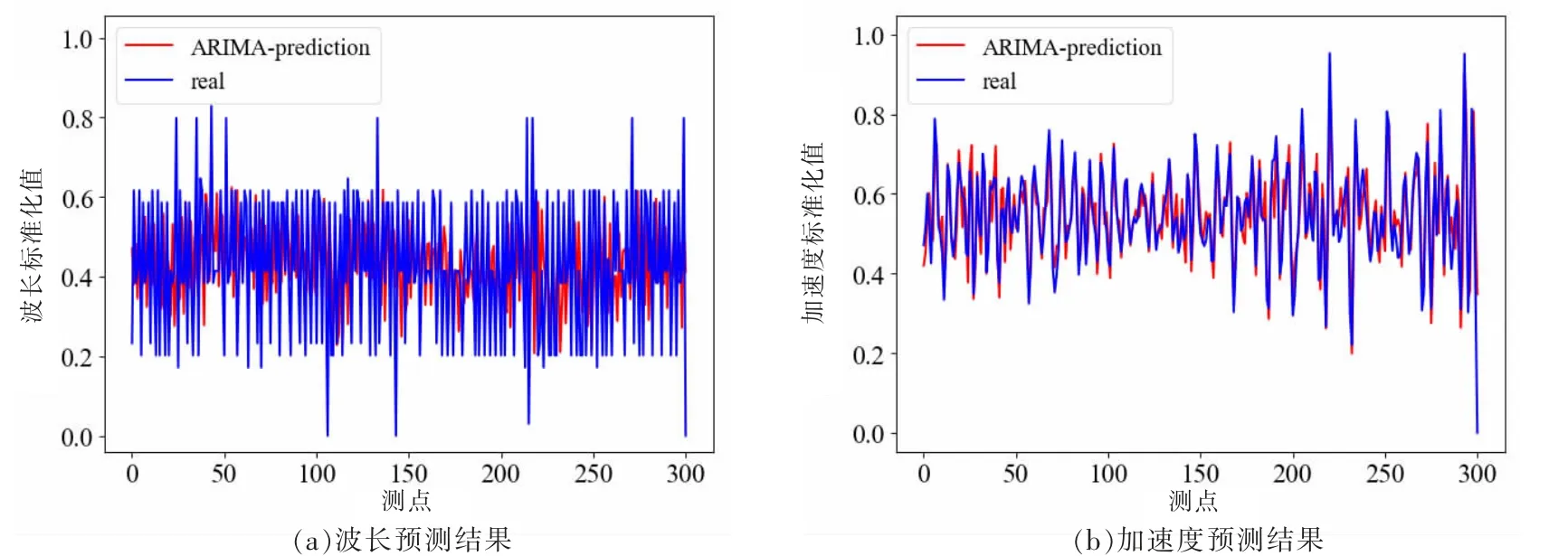
图8 ARIMA预测效果图

4.3 预测结果的对比分析

本文采用了绝对百分比误差最大值（MAX）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及均方根误差（RMSE）等作为评价指标，来评估LSTM和ARIMA模型在预测值和实测值之间的差距；R2用于判断模型好坏，具体公式[9]如下所示。

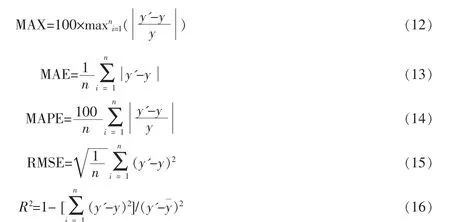
其中，n为测试样本总数，y'为样本预测值，y为样本实测值为样本实测均值。

几种评价指标的对比结果如表3所示。结果显示，除了对加速度数据预测的RMSE外，LSTM模型的MAX、MAE、MAPE均小于ARIMA模型的相应指标；LSTM模型的R2值大于ARIMA模型的R2值，说明LSTM模型的整体预测效果优于ARIMA模型。比较模型训练时间，ARIMA大概为338 s，而LSTM大概为880 s，效率稍低。

表3 模型误差指标

5 结论

本文针对结构健康监测中的两种时间序列数据：FBG波长时程信号和加速度时程信号，建立LSTM和ARIMA两种模型，对动态监测信号的缺失数据进行了预测分析，并对两种模型的预测效果进行了对比。波长和加速度数据首先进行标准化处理，进行一定长度的截断，作为两种模型的训练集和测试集。在LSTM模型中，通过比较10组超参数对计算效率和精度的影响，选择确定本文所用LSTM模型的超参数。由于ARIMA模型对时间序列数据有平稳性要求，对波长和加速度数据进行了ADF检验。最后，采用绝对百分比误差最大值（MAX）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及均方根误差（RMSE）等指标，评估了LSTM和ARIMA模型的预测效果。结果表明，LSTM模型的整体预测效果优于ARIMA模型，但在预测耗时方面，LSTM模型的效率较低。实际工程应用中，可根据数据的量级来选择训练集的大小。小规模数量级中，划分70%作为训练集。大规模数量级中，可增大训练集的比例至98%、99%。预测误差随着数据丢失率增加而增加。至于丢失多少比例后预测会失真，这是后续研究要解决的问题，课题组其他成员正结合其他算法进一步评估预测数据的有效性。