材料类型对可更换耗能梁段滞回性能的影响分析

闵益新，孙国华，杨伟兴

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.中衡设计集团股份有限公司，江苏 苏州 215123）

在高层偏心支撑钢框架结构中，增设耗能梁段可显著提高结构的抗侧刚度、水平承载力及耗能能力。利用耗能梁段的剪切屈服可提供稳定的滞回耗能，在强烈地震作用下具有良好的延性行为，但产生的损伤导致其震后不易更换，增加修复难度。Fortney等提出了可更换连梁概念，连梁两端采用连接板、螺栓与主体结构连接，震损后拆卸方便[1]。Mansour N等进行了13个耗能梁段的循环加载试验，结果表明普通钢材耗能梁段表现良好的变形能力，屈服后具有稳定的耗能特征[2]。殷占忠等对8个不同参数的可更换钢耗能梁段进行了数值模拟，分析表明耗能梁段滞回曲线呈饱满的梭形，具有良好的耗能能力[3]。Nastri E等通过数值模拟方法研究了轴向约束对普通钢耗能梁段滞回性能的影响，发现轴向约束会提高其极限变形能力和超强性能[4]。近年来，国内外学者提出采用低屈服点钢代替普通碳素钢。美国学者Peter Dusicka对LYP100钢材进行了循环加载性能试验，发现低屈服点钢材循环硬化比普通钢材略高[5]。温东辉等对宝钢生产的三种低屈服点钢材进行了力学性能研究，证实了低屈服钢材塑性变形能力强且焊接性能良好[6]。石永久等进行了大量的低屈服点钢材的力学性能研究，发现低屈服点钢材具有明显的循环硬化行为和良好的耗能能力[7-8]。部分学者开展了低屈服点钢耗能梁段的相关研究，段朝升等研究了低屈服点钢可替换耗能梁段对K形偏心支撑钢框架滞回性能的影响，试验证实了低屈服钢材耗能梁段的转动能力和塑性变形能力更优[9]。

此外，越来越多的新型功能材料在土木工程领域推广应用。不锈钢材料因具有良好的耐腐蚀性、耐久性、耐高温性，以及良好的延性和塑性变形能力[10]，在大型结构中应用越来越多。符晓对7个不锈钢耗能梁段进行了拟静力加载试验，试验结果表明不锈钢耗能梁段具有较好的延性和变形能力，且抗震性能比普通碳素钢更优[11]。铝合金因其密度低，且具有较好的延展性，备受建筑师青睐。贾斌等利用国产铝合金材料制作防屈曲耗能支撑，并进行了循环力学性能的试验和理论研究，结果表明铝合金材料表现出明显的循环强化特征，延性性能良好[12]。张益康提出将铝合金作为防屈曲支撑的核心单元，通过有限元模拟证实了铝合金防屈曲耗能支撑呈现良好的承载能力和耗能能力[13]。目前，尚未有学者对铝合金耗能梁段开展相关研究工作。

本文对普通钢材、不锈钢材、铝合金制作的耗能梁段进行了数值模拟分析，系统研究了三种材料对可更换耗能梁段滞回性能、抗剪承载力、变形能力、耗能能力及超强性能的影响规律，分析结果可为耗能梁段的工程应用提供参考。

1 算例设计及有限元模型

1.1 算例设计

本文设计了三种不同材料的可更换耗能梁段，分别采用普通Q235B级钢材、S30408级不锈钢材、6061-T6级铝合金材料，试件编号分别为M-1、M-2、M-3，其几何尺寸见图1。耗能梁段长度为660 mm，截面为焊接工字形H250 mm×100 mm×6 mm×10 mm，腹板高厚比为38.3，翼缘宽厚比为4.7，均满足我国建筑抗震设计规范（GB 50011-2010）[14]的相关要求。耗能梁段两侧端板及加劲肋均采用Q235B，加劲肋双面布置，其厚度为6 mm。耗能梁段长度比为1.25，属于剪切型耗能梁段。耗能梁段与端板之间焊接。为确保耗能梁段处于剪切受力状态，设计了一套铰接框架，钢柱上、下部通过板铰与顶梁及底梁连接，通过平行机构施加水平剪力。耗能梁段两侧端板采用12.9级M24高强螺栓与顶梁及底梁连接。

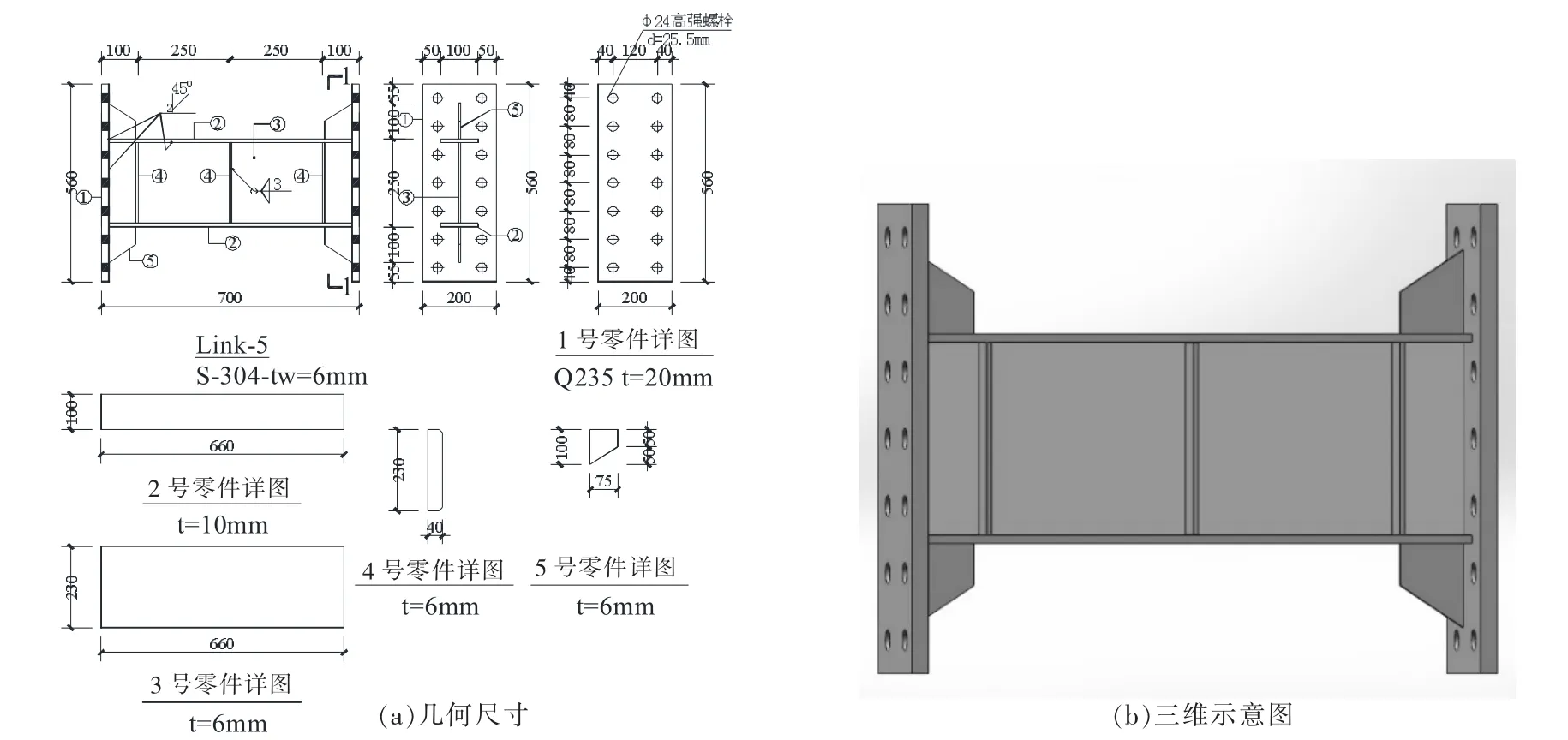
图1 耗能梁段的几何尺寸及三维示意

1.2 有限元模型的建立

采用ABAQUS程序建立耗能梁段及加载装置的精细化有限元模型。其中，耗能梁段采用壳单元S4R模拟，其余构件均采用C3D8R实体单元模拟。为确保分析精度，对耗能梁段采用细分网格方式，单元网格尺寸取25 mm，销轴、耳板、连接板及其他构件采用略粗网格，且采用中性轴算法的六面体扫掠网格划分。图2给出了耗能梁段及加载装置的有限元模型。

图2 耗能梁段及加载装置的有限元模型

根据《钢结构设计标准》（GB50017-2017）[15]中对普通碳素钢材力学性能指标的规定，Q235B钢材的屈服强度取fy=235 MPa，极限抗拉强度fu=370 MPa，采用三折线模型模拟钢材非线性，弹性模量E=2.06×105MPa，屈服后模量Et=0.01E，泊松比ν=0.3。根据《不锈钢结构技术规程》（CECS410-2015）[16]中对不锈钢材材料力学性能指标的有关规定，S30408不锈钢的名义屈服强度fy=205 MPa，极限抗拉强度fu=515 MPa，弹性模量E=1.93×105MPa，泊松比ν=0.3。根据《铝合金结构设计规范》（GB50429-2007）[17]中对铝合金材料力学性能指标的规定，6061-T6铝合金取屈服强度fy=240 MPa，极限抗拉强度fu=260 MPa，弹性模量E=0.7×105MPa，泊松比ν=0.3。

耗能梁段模型中涉及的销轴与耳板、销轴与连接板等之间均采用面面接触。考虑到试验加载过程中接触面间存在一定的滑移，接触面法向设置硬接触，接触面切向设为有限滑移，摩擦系数取0.15。用于加载的顶梁和地梁与铰接支座之间，以及顶梁和地梁与垫梁之间、加劲肋和耗能梁段腹板与翼缘之间均采用Tie连接，垫梁与耗能梁段壳单元之间采用Shell-to-SolidCoupling连接。地梁底部设置为固定约束，加载梁顶部面外方向设置水平位移约束（见图3），用于模拟限位装置对耗能梁段的约束作用，对加载梁端截面中心设置参考点，并通过在参考点上施加位移方式来实现循环加载，加载制度参考美国AISC 341-10建议[18]。

图3 加载制度

2 试验验证

本文对文献[19]的试验试件M-2进行了有限元验证。图4给出了试验试件M-2在层间位移角0.09 rad时变形及Mises应力分布。由图4可知，试件M-2呈现明显的剪切变形特征，且变形集中于腹板的下部区格。有限元分析得到的变形模式与试验结果基本一致，腹板出现明显局部屈曲变形，腹板上部区格内变形相对较小，Mises应力均已超越显著屈服。因此，从宏观现象来看，精细化有限元分析能够捕捉不锈钢耗能梁段的变形特征，模拟结果可信。

图4 变形模式对比

图5给出了试验试件M-2的试验结果及数值模拟对比。由图5可知，有限元模拟得到的滞回曲线略显饱满，这是由于不锈钢材料的实际本构模型与模拟采用的本构模型仍存在一定差异所致。此外，有限元模拟未能精确考虑试件的初始几何缺陷，以及试验试件在加工过程中所存在的其他缺陷。精细化有限元模型未能精确反映试件M-2腹板出现裂纹后的力学性能。但从整体来看，有限元方法仍能较为精确地分析其滞回特征、水平承载力、抗侧刚度与极限变形能力。

图5 滞回曲线对比

3 耗能梁段材料的影响分析

3.1 Mises应力分布

图6给出了三个耗能梁段模型在层间位移角0.09 rad时的Mises应力云图。由图6可知，材料类型对耗能梁段Mises应力水平影响较大。达到相同层间位移角时，三个模型的腹板均已屈服，耗能梁段两侧翼缘发生明显弯曲变形。不锈钢耗能梁段的Mises应力水平最高，达到了352 MPa，铝合金耗能梁段腹板的屈服程度最为严重，且腹板全截面均匀屈服。三个耗能梁段模型均呈明显的剪切屈服变形特征。

图6 材料对耗能梁段Mises应力的影响

3.2 滞回曲线

图7给出了三个耗能梁段模型的滞回曲线。由图7可知，三种材料的耗能梁段滞回曲线均较为饱满，塑性发展充分。与其他材料相比，不锈钢耗能梁段在达到显著屈服后，其水平承载力强化明显。铝合金耗能梁段加载及卸载的剪切刚度均较低，其在层间位移角达到0.05 rad后，出现下降，且因腹板局部屈曲导致波形转变，导致滞回曲线抖动明显，其变形能力也未能得到充分发挥。

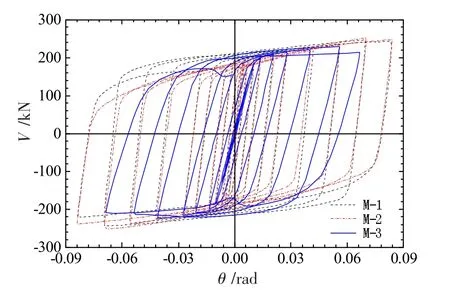
图7 材料对其滞回特征的影响

3.3 骨架曲线

骨架曲线是将滞回曲线上各级荷载的峰值点依次相连所得到的曲线，可直观反映出构件在不同加载阶段的抗剪承载力、变形能力等特征。图8给出了三个耗能梁段模型的骨架曲线。由图8可知，三个耗能梁段模型骨架曲线呈双线性特征。在弹性阶段，水平承载力增加迅速，但采用不锈钢材料的M-2模型屈服后承载力增加更为显著，强化特征明显，其平均峰值承载力为252.7 kN。铝合金材料耗能梁段的抗剪承载力最低，其平均峰值承载力为218.9 kN。

图8 材料对耗能梁段骨架曲线的影响

3.4 抗侧刚度

构件在加载过程中累积损伤可通过刚度退化间接反映，本文通过割线刚度来描述模型的刚度退化规律。图9给出了三个耗能梁段模型的抗侧刚度退化曲线。由图9可知，因不锈钢与普通碳素钢材的初始弹性模量相差不多。因此，其初始弹性抗侧刚度差异较小，试件M-1试件的初始弹性抗侧刚度为73.6 kN/mm，试件M-2的初始弹性抗侧刚度为66.1 kN/mm。因铝合金材料的初始弹性模量最小，因此导致的模型M-3的初始弹性抗侧刚度仅为38.8 kN/mm。在层间位移角达到0.01 rad后，三个耗能梁段的抗侧刚度退化趋势基本一致，且退化速度均匀缓慢。

多元相关系数(R)=0.953。说明，产量受多个主要农艺性状的综合影响，在生产中要综合考虑，合理安排各个因素水平。

图9 材料对耗能梁段抗侧刚度的影响

3.5 延性及变形

延性是指材料、构件或结构在达到显著屈服后承载力无明显下降的变形能力，通常情况下构件的延性可用延性系数量化。表2给出了三个耗能梁段的延性系数。由表2可知，由于铝合金耗能梁段的抗侧刚度最小，导致其显著屈服位移最大，致使其位移延性系数最小，仅为4.9。不锈钢及普通钢材耗能梁段的抗侧刚度均较大，其显著屈服位移相对较小，其位移延性系数在10.3～11.5之间。尽管两者的延性系数存相差较小，但其极限位移相差较大，这充分说明评估结构或构件应根据极限变形能力及延性综合评判。

表2 模型的位移延性系数

3.6 耗能能力

耗能能力指的是结构或构件在地震作用下吸收能量的大小，是评估结构抗震性能的重要指标，通常采用无量纲的等效黏滞阻尼比衡量。图10给出了三个耗能梁段模型的等效黏滞阻尼比。在三个耗能梁段模型达到显著屈服后，形成了较为饱满的滞回曲线，耗能能力显著增加，其等效黏滞阻尼比迅速增大。三个耗能梁段模型中，采用不锈钢及普通钢材的耗能梁段具有较好的耗能能力，其最大等效黏滞阻尼比已超越0.46。采用铝合金材料的耗能梁段等效黏滞阻尼比略低，为0.385，耗能能力略低。

图10 材料对耗能梁段等效黏滞阻尼比的影响

3.7 超强系数

结构或构件的超强性能起到了避免其在遭遇强烈地震作用下发生倒塌破坏，一般可采用超强系数来定量描述，定义为RΩ=Vu/Vd；Vp=fyAW。式中，RΩ为超强系数；Vd为耗能梁段的设计剪力；Vu为耗能梁段的峰值剪力。

表3给出了三个耗能梁段模型的超强系数。由表3可知，不锈钢材料的耗能梁段其超强系数最大，承载力强化最为显著。

表3 模型的超强系数

4 结论

（1）不锈钢耗能梁段塑性变形发展最充分，主要通过腹板剪切变形和翼缘端部的弯曲变形耗散能量。

（2）不锈钢耗能梁段承载力强化显著，更易获得更高的水平承载力，普通钢耗能梁段次之，铝合金材料的耗能梁段水平承载力最低，峰值承载力降低约9.5%。

（4）不锈钢及普通钢材耗能梁段的耗能能力最优，最大等效黏滞阻尼比约为0.46；铝合金耗能梁段的耗能能力一般，最大等效黏滞阻尼比为0.385。

（5）不锈钢耗能梁段超强性能最优，其超强系数为1.49，分别比普通钢耗能梁段高17.3%，比铝合金耗能梁段高29.6%。