基于鲸鱼算法优化LSSVM的铣刀磨损监测
张庆华, 龙 伟, 李炎炎, 林 懿
(四川大学机械工程学院, 成都 610065)
1 引 言
智能制造作为新一轮产业升级的重要方向,正在给全球制造业带来深刻的变革.在机械加工制造中,设备的故障诊断是重点研究领域[1],刀具的磨损状态对工件的质量有着直接的影响[2],当刀具磨损到一定程度时,如果继续使用,则会引起切削力、切削温度及切削振动等明显变化,降低切削性能,甚至导致工件报废[3].研究表明[4,5],刀具的磨钝和破损会导致生产加工的时间成本与经济成本的上升,刀具磨损状态监测技术可以提高生产效率,降低生产成本,具有重要意义.
刀具磨损状态可以通过直接法和间接法进行监测[6].接触测量法和机器视觉测量法[7]常用于直接监测刀具的磨损.由于直接法的实施成本过高,不适合实际应用,目前主要采用间接法实现刀具磨损状态的监测.加工过程中,切削力、振动等信号与刀具磨损量密切相关,间接法通过分析这些信号实现对刀具磨损状态的间接监测,其过程可分为信号采集、特征提取和模式识别[8].
能否准确地提取与刀具磨损相关的特征直接关系到刀具磨损状态识别的结果好坏.常用的特性提取方法有:时域分析、频域分析、小波分解和经验模态分解(Empirical Mode Decomposition,EMD)等.时域分析与频域分析是分别对信号进行时频域处理,获得时域特征与频域特征,不能兼顾信号在时域和频域中的变化,对于非平稳信号效果不佳.Somkiat等[9]提出了一种基于小波变换的刀具磨损监测系统,利用小波变换区分刀具磨损信号与噪声.孙巍伟等[10]利用EMD处理机加工过程产生的振动信号,并结合隐马尔可夫模型进行刀具磨损故障诊断.Dragomiretskiy等[11]提出了一种完全非递归的变分模态分解(Variational Mode Decomposition,VMD)方法,VMD解决了EMD出现的模态分量混叠问题[12].王向阳等[13]使用VMD方法处理铣削加工产生的振动信号,提取每个固有模态分量(Intrinsic Mode Function,IMF)的中心频率和能量作为特征向量,结果表明相较于EMD方法,VMD更加适用于铣刀破损检测.因此,本文采用VMD对振动信号进行特征提取.
在磨损状态识别方面,关山等[14]采用最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)实现了刀具磨损量的测量,证明了该方法相比于神经网络算法,拥有更高的精度.但是,LSSVM方法对参数的取值非常敏感,模型参数的取值对识别精度的影响大[15].为了解决LSSVM的参数选择问题,刘成颖等[16]引入粒子群算法(Particle Swarm Optimization,PSO)优化LSSVM模型的惩罚因子和核参数,但是该算法存在局部极值,易早熟收敛等缺点.本文针对上述问题,提出一种基于改进的鲸鱼算法优化最小二乘支持向量机的刀具磨损监测方法.首先,采用VMD对振动信号进行分解,提取每个模态的能量熵和时频域特征,归一化处理后作为特征向量.然后,采用改进的鲸鱼算法优化LSSVM模型的惩罚因子和核参数.最后,将本文提出的模型应用于刀具磨损状态监测,结果表明,该方法具有更高的识别精度.
2 鲸鱼优化算法
鲸鱼优化算法(Whale Optimization Algorithm,WOA),是一种模拟座头鲸群体捕食行为的智能优化算法[17,18].在该算法中,鲸鱼种群相当于待求解问题的解空间,每个鲸鱼个体代表一个可行解,鲸鱼在全局中的最优位置表示WOA算法中的最优解.由于初始状态下,全局最优位置是未知的,故先找出当前鲸鱼种群中适应度值最优的个体,将其视为目标猎物,其他鲸鱼个体通过收缩包围、气泡网捕食和随机搜索三种方式更新自身位置,其过程如下.
2.1 收缩包围
在收缩包围阶段,鲸鱼首先识别目标猎物并将其包围,种群中的其他个体均向目标猎物位置移动,位置更新公式如下.
D=|CX*(t)-X(t)|
(1)
X(t+1)=X*(t)-AD
(2)
式中,A=2ar-a;C=2r;t表示当前的迭代次数;r表示[0,1]的随机数;a表示收敛因子,初始值为2,之后线性递减为0.
2.2 气泡网捕食
气泡网捕食过程中,鲸鱼通过螺旋更新位置和收缩包围进行捕食,二者是同步进行的,为了模拟这一过程,引入概率p在二者之间选择,当p<0.5时,鲸鱼通过式(2)收缩包围;当p≥0.5时,搜索代理通过螺旋模型更新位置,其数学模型如下.
X(t+1)=D′eblcos(2πl)+X*(t)
(3)
式中,b为对数螺旋形状常数;l为区间[-1,1]中的随机数.
2.3 随机搜索
当|A| ≥ 1时,搜索代理不再基于目标猎物更新位置,而是根据彼此的位置进行全局搜索,以便增强WOA的全局搜索能力,随机选择当前种群中的一个搜索代理,表示为Xrand(t),随机搜索公式表述为
X(t+1)=Xrand(t)-AD
(4)
3 改进的鲸鱼优化算法
传统鲸鱼算法的优点在于调节参数少,可以较好的平衡开发与勘探能力[19],然而由于线性收敛因子的存在,使得WOA算法在迭代过程的前期,具有一定的全局搜索能力,而迭代的后期,陷入局部最优解的可能性大,影响WOA算法的收敛精度.
为克服WOA算法存在的上述缺陷,笔者提出一种改进的鲸鱼算法(Improved Whale Optimization Algorithm,IWOA).相比于传统鲸鱼算法,IWOA在迭代中引入混合反向学习策略,同时改进收敛因子,以提升算法的全局搜索能力和收敛速度.具体的改进措施如下.
3.1 混合反向学习算法
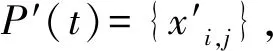
(5)
其中,l为反向学习因子,是区间[0,2]上的随机数;xmax, j和xmin, j分别为搜索代理xi的第j维元素最大值和最小值.然后,计算当前种群个体适应度fitness(i)与反向种群个体适应度fitness′(i),若反向种群适个体应度优于当前种群个体,则用反向种群个体代替当前种群个体.
3.2 非线性收敛因子
标准鲸鱼算法的全局探索与局部开发能力依赖于系数A,而系数A的值是由收敛因子a确定的,收敛因子是线性递减的,使得鲸鱼算法在迭代前期收敛因子较大,因而具有较强的全局探索能力,在迭代后期,收敛因子较小,算法倾向于进行局部开发,这使得算法在复杂的非线性搜索过程中收敛速度慢,容易陷入局部最优解.因此,本文提出一种分段的非线性收敛因子,具体公式如下.
(6)
在整个迭代过程中,非线性收敛因子分别在前半段和后半段从2减小到0,并且前半段下降的速度逐渐增大,后半段下降的速度逐渐减小,使得改进后的鲸鱼群算法可以更好地适应复杂的搜索过程.IWOA算法流程如下.

图1 IWOA算法流程图Fig.1 Flow chart of IWOA algorithm
4 IWOA算法性能测试
采用4个基准测试函数(如表1)验证IWOA算法的性能,其中f1和f2为单峰基准函数,f3和f4为多峰基准函数.在进行对比测试时,将本文提出的IWOA算法与WOA算法、灰狼优化算法(Grey Wolf Optimizer,GWO)、引力搜索算法(Gravitational Search Algorithm, GSA)、粒子群算法(Particle Swarm Optimization, PSO)法进行对比,为使测试结果更加客观,所有算法的设置保持一致,种群规模均设置为30,最大迭代次数均设置为500,测试结果见图2~图5.

表1 4个基准测试函数Tab.1 Four benchmark test functions
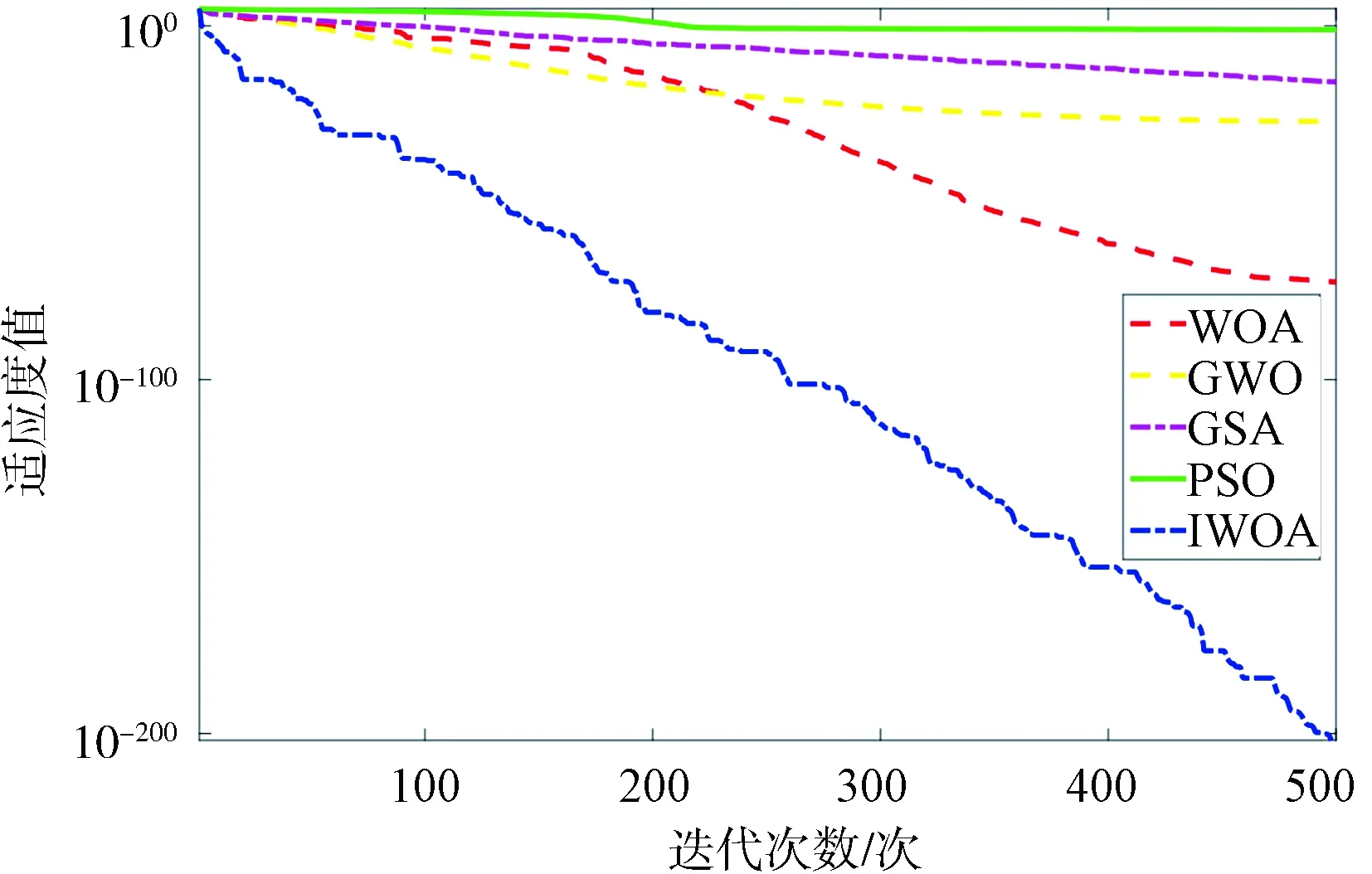
图2 f1函数优化曲线Fig.2 The optimization curve of f1 function
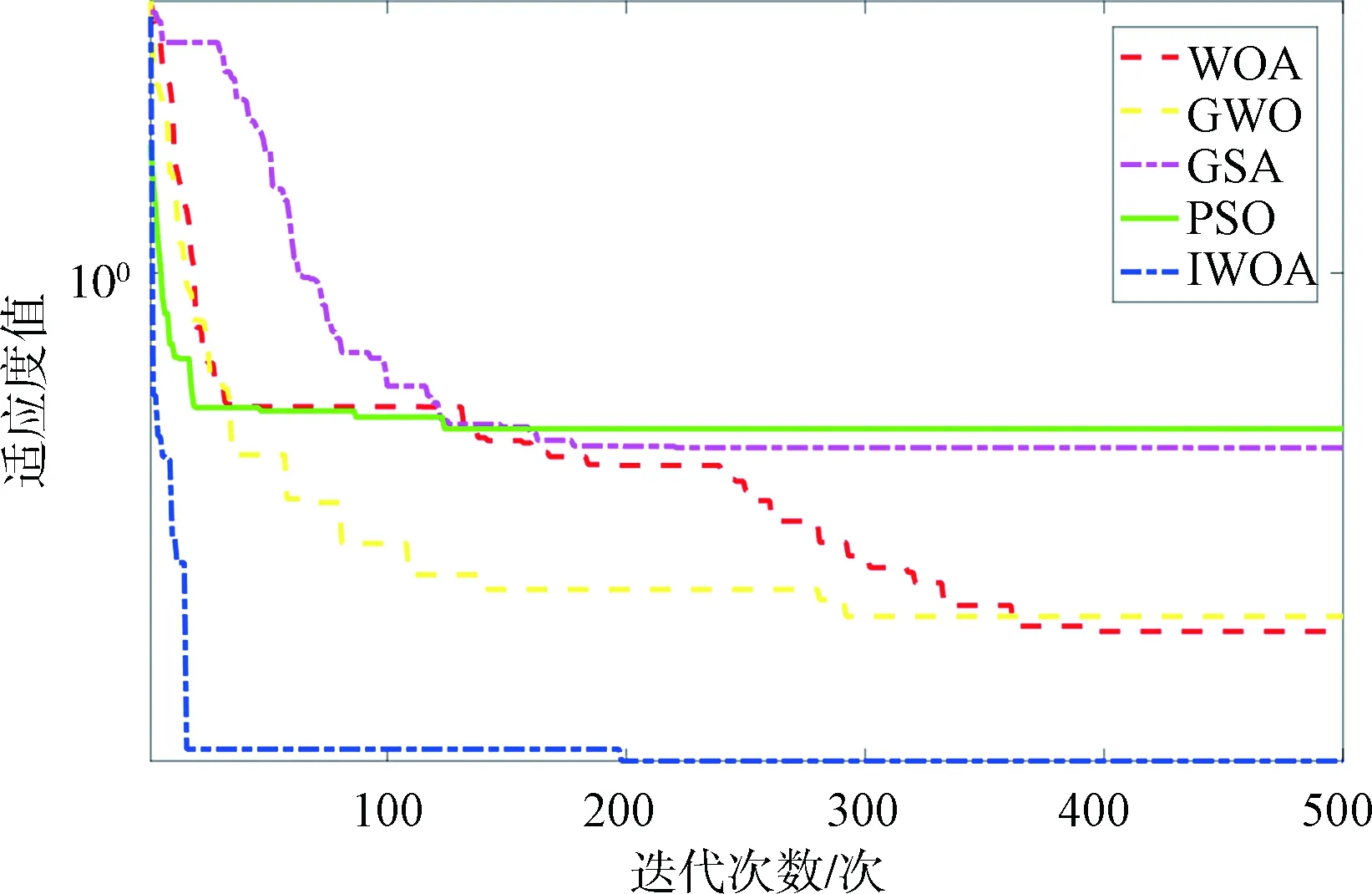
图3 f2函数优化曲线Fig.3 The optimization curve of f2 function
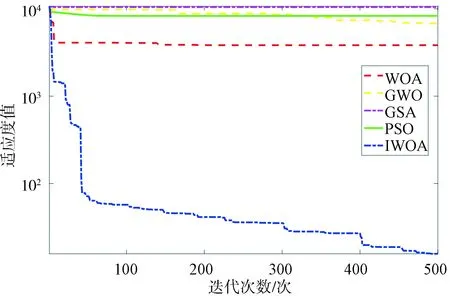
图4 f3函数优化曲线Fig.4 The optimization curve of f3 function
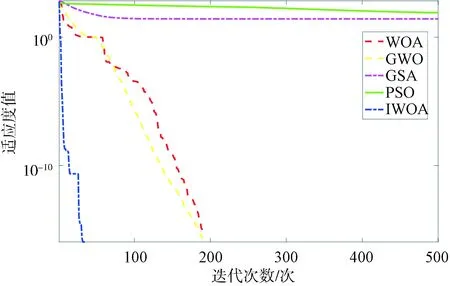
图5 f4函数优化曲线Fig.5 The optimization curve of f4 function
通过对4个基准测试函数的仿真结果可以看出,在优化单峰函数与多峰函数时,IWOA算法的收敛精度与收敛速度明显优于其他4种对比算法.在对f4函数的优化中,IWOA算法与WOA、GWO算法均能收敛到全局最优,而IWOA的收敛速度要优于WOA与GWO,这验证了IWOA算法的可行性与高效性.故将本文提出的IWOA算法用于优化LSSVM模型,对惩罚因子γ和核参数σ寻优,以提高模型的识别率.
5 实验分析
实验采用PHM Society 2010年提供的铣刀磨损数据集,该数据集共分为6组,每组数据包含X、Y、Z三个方向的铣削力信号和振动信号以及声发射信号的均方根值,本文采用第6组数据中X、Y、Z三个方向的振动信号进行实验.首先使用VMD分解信号,得到IMF分量,提取IMF分量的时域特征与能量熵作为特征向量.在进行VMD分解时,分解数K的确定对分解效果至关重要,以X方向振动信号为例,当K=5时,出现了模态交叠现象(IMF4与IMF5,如图6所示),因此取K=4.采用同样的方法,可以确定分解Y方向振动信号、Z方向振动信号时,K的值取3可以较好地分解信号.
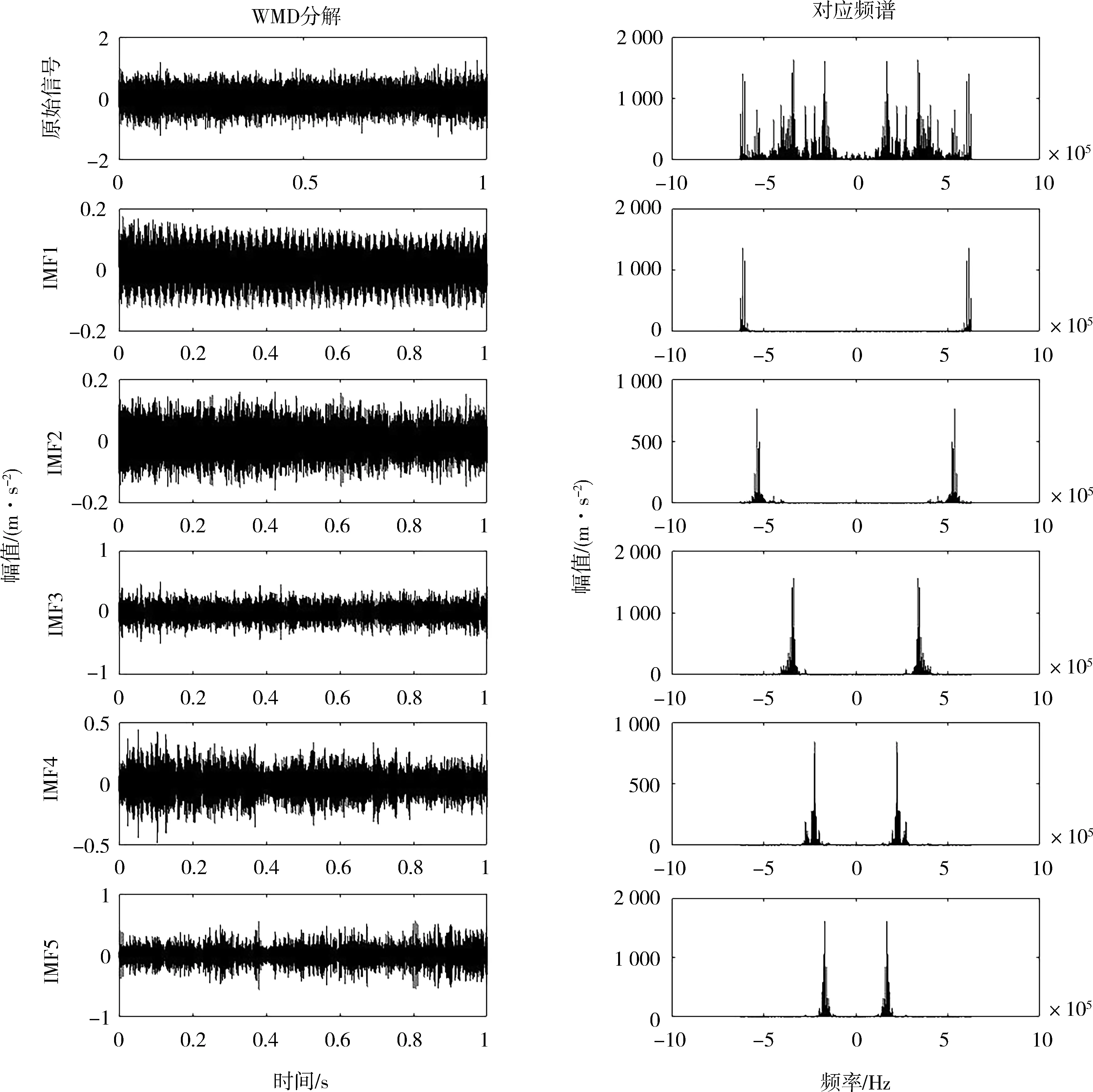
图6 K=5时的VMD分解结果Fig.6 VMD decomposition result when K=5
5.1 特征选择
X、Y、Z三个方向振动信号经VMD分解后,共得到10个IMF分量,提取每个IMF分量的17个时域特征与能量熵,所以总共得到180个特征.这些特征并非都与磨损量相关,为了避免不必要的计算,提高模型识别率,需要进行特征选择[20],本文采用相关系数法与灰色关联度分析法进行特征选择.
相关系数(Correlation Coefficient)用于衡量变量之间关系密切程度,其中,皮尔逊相关系数广泛应用于衡量两个变量之间的线性关系[21],其公式如下.
(7)
式中,E表示期望.|ρX,Y|的取值范围为[0,1],相关系数越接近1,说明X、Y线性相关性越好,反之,线性相关性越差.
灰色关联度分析(Grey Relation Analysis, GRA)是一种多因素统计分析方法[22],其通过确定参考列和比较列的几何形状相似程度来衡量二者之间的关联程度,它反映了参考列与比较列非线性关系.假设比较列为xi,参考列为x0,灰色关联系数为ζi(k).
(8)
(9)
式中,ρ为分辨系数,一般取0.5.对每个维度进行计算,得到一个新的序列,这个序列中的每个点就代表着该子序列与母序列对应维度上的关联性.根据灰色关联系数可得到关联度,xi与x0的关联度公式如下.
(10)
利用皮尔逊相关系数与灰色关联度分析特征向量与刀具磨损之间的相关性,以皮尔逊相关系数大于0.9并且关联度大于0.9为标准对特征向量进行选择,最终筛选出16个特征,如表2所示.

表2 特征选择结果Tab.2 Feature selection results
(a)
5.2 磨损状态识别
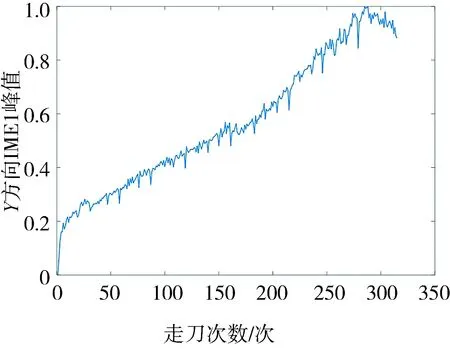
铣刀磨损数据共有315组,分别包含球头铣刀X、Y、Z三个方向的磨损量,本文取X、Y、Z三个方向磨损量的平均数作为铣刀的磨损值.然后使用K均值聚类法将磨损状态分为5类,第一类为1~27;第二类为28~80;第三类为81~208;第四类为209~259;第五类为260~315.随机选择数据样本的80%作为训练样本,剩下20%作为测试样本,并采用5折交叉验证法,以避免模型过拟合与欠拟合.运行10次,取平均分类正确率为评价标准.
仿真实验在MATLAB 2016a平台上进行,为了验证本文提出的算法的有效性,分别采用WOA算法、GWO算法、GSA算法与PSO算法优化LSSVM作为对比,仿真结果如表3所示.
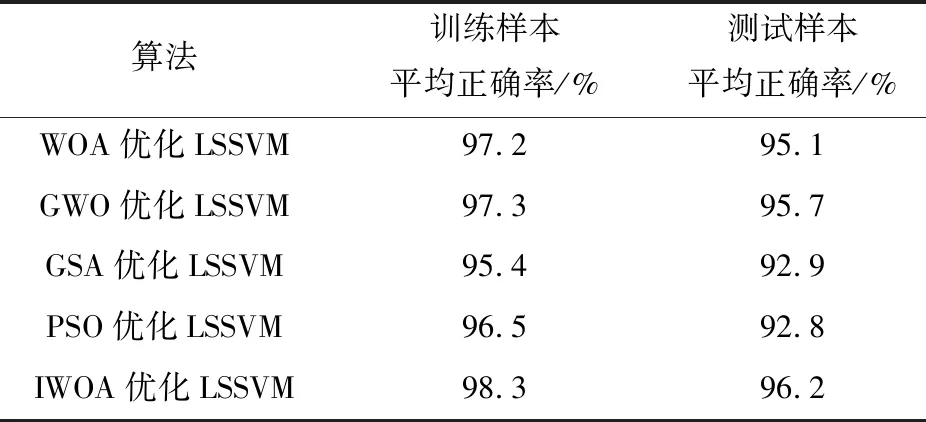
表3 实验仿真结果Tab.3 Experimental simulation results
6 结 论
本文提出了一种IWOA算法优化LSSVM模型,采用VMD方法对铣削振动信号进行分解,提取IMF分量的时域特征与能量熵构成特征向量,引入混合反向学习算法和非线性收敛因子对鲸鱼算法进行改进,并采用4种基准测试函数验证了改进后的鲸鱼算法的性能,将其应用于铣刀磨损状态监测,识别结果与WOA-LSSVM、GWO-LSSVM、GSA-LSSVM和PSO-LSSVM模型对比.结果表明,IWOA-LSSVM模型具有更高的识别精度,为铣刀磨损状态的在线监测提供了一种新方法.

