基于改进灰狼优化算法的点云配准

杨沐杰，钟羽中，郭 斌，佃松宜

(四川大学电气工程学院，四川 成都 610065)

1 引言

不同视角下点云数据的配准是对物体外观进行三维重建的关键步骤，它一直是计算机视觉、逆向工程、曲面质量检测、SLAM等[1-3]多个领域的热点和难点。在不考虑发生形变的情况下，点云配准的本质就是求解不同视角下点集的刚体变换矩阵，使这些点集属于物体相同部分的点进行重合。点云配准主要分为粗配准和细配准两个部分，粗配准是将两片点云进行大致位置上的重合，它的意义在于减少两片点云的旋转平移差，为细配准提供较好的初值；细配准则是将粗配准后的点云进行重合，使得误差最小化。通过粗略和精细两个部分的配准去寻找到一个合适的变换矩阵对点集进行匹配重合，直接影响着整个三维重建的精度。

当前在点云配准中引用最广泛的经典算法就是迭代最近点(iterative closest point，ICP)法[4]，算法是在1992年由一位名叫Besl的学者所提出，其基本思想是通过最近邻搜索法找到源点云每个点在目标点云的最近点，求解出变换矩阵后再作用于源点云以更新位置，直到满足要求。但算法计算量过大且对点云的初始位置要求较高，若位置相差过大会导致配准精度低甚至配准失败，国内外学者们相对应提出了不少改进的方法，如张蒙[5]在引入k-dtree的同时，添加了欧式距离和方向向量阈值对算法进行改进，提高了配准效率和精度；Du[6]利用仿射法解决了ICP的仿射配准问题等，但仍然存在着配准精度低的问题。故在点云粗配准阶段将两片点云的位置变换到细配准算法的收敛范围内显得更为重要。

灰狼优化算法[7]是Seyedali.Mirjalili从灰狼群体捕食的行为受到启发，在2014年提出的一种新的元启发式算法，它根据灰狼捕食时严格遵守的社会等级关系，由等级最高的三头狼自上而下，使其在各自的区域内进行搜索完成优化工作。灰狼优化算法有着较强的收敛能力，且算法参数少，易于实现，但同时也存在着收敛速度慢、容易早熟，陷入局部最优等问题。针对此，国内外学者提出了各种改进方法，如魏政磊[8]提出一种自适应搜索的方法来提高算法的收敛速度和优化精度；Saremi[9]使用进化种群动态操作(Evolutionary Population Dynamic，EPD)加入到灰狼优化中，剔除当中适应度差的个体以增强GWO的寻优能力；Zhu[10]利用差分进化的方法来更新灰狼优化中3个头狼的位置，提高了算法的收敛速度和收敛精度。

本文首先针对单一灰狼优化算法局限性大，在保证其收敛精度的同时却丢失了其收敛速度等问题，考虑到差分进化算法因其优秀的寻优能力常用来与其它智能算法相结合来提高原算法的优化能力[11]，故将差分进化算法和灰狼优化算法进行结合并加以改进，在加快算法收敛速度的同时也能提高算法解的精度。其次为解决ICP算法对点云初始位置要求高且配准精度低等问题，将改进后的灰狼优化算法引入到点云的粗配准之中，再与细配准中的ICP算法相结合，对整个配准过程进行优化。对比传统的ICP算法后，发现改进后的配准算法在配准时间和配准精度上都有着一定程度的提高。

2 基于改进灰狼优化算法的点云配准

在三维重建领域中，针对不同视角点云的配准问题一直是重点和难点，为解决传统ICP算法配准速度慢且对初始位置要求高等问题，本文提出一种改进的点云配准方法，在粗配准中对灰狼优化算法进行改进并与差分进化算法相结合，生成一种新的混合算法：DE-GWO算法，使用DE-GWO算法对配准参数进行寻优为细配准提供良好初值，后续精细配准中使用传统ICP算法并稍作优化，使用此方法对配准过程进行优化，同时提升了配准的速度和精度。

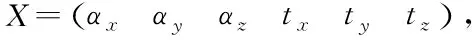
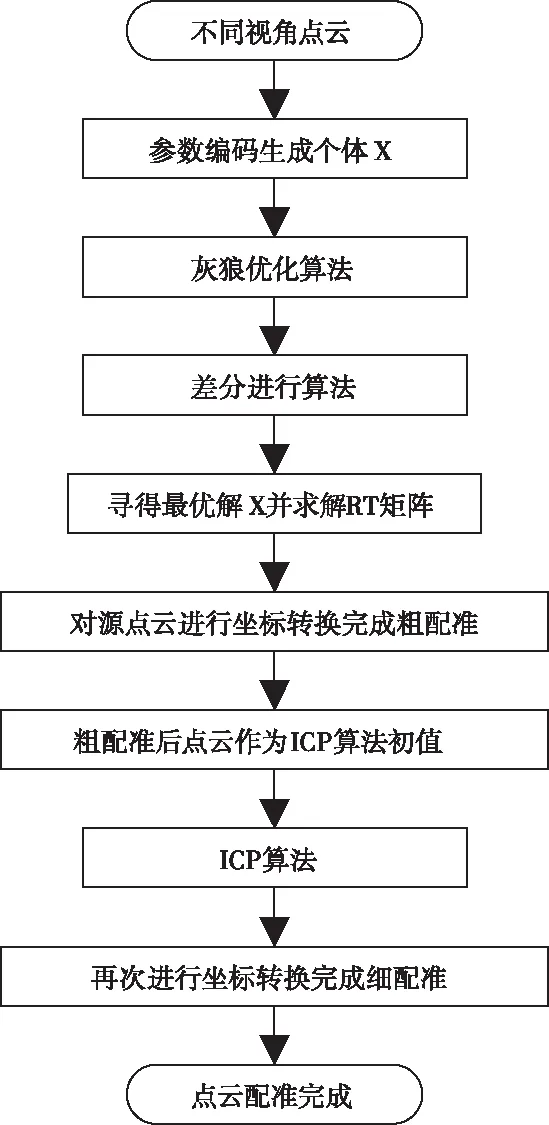
图1 点云配准流程图

粗配准中使用的DE-GWO算法在算法迭代过程中的前期阶段，先使用灰狼优化算法，并在搜索阶段引入分段搜索的思想，保证算法全局搜索的能力，以免早熟，陷入局部最优。在灰狼算法后期生成候选解时，使用贪心法则，将其它三个解也同时当作候选解，并通过计算适应度函数来选择最优解。而在迭代后期，将灰狼优化得出的最优候选解代入差分进化算法中，对变异策略进行改进再经交叉、选择之后生成优秀个体，并更新下一次迭代的三个头狼，反复迭代直到寻得最优解。

算法先使用灰狼优化算法更新种群位置，以便在前期得到不错的优化精度，之后再使用差分进化算法对其进行变异更新，增强后期局部搜索性，以保证更优秀的寻优效率和精度。改进后的DE-GWO算法流程图如图2所示，其中d为迭代次数，r对应每个个体。

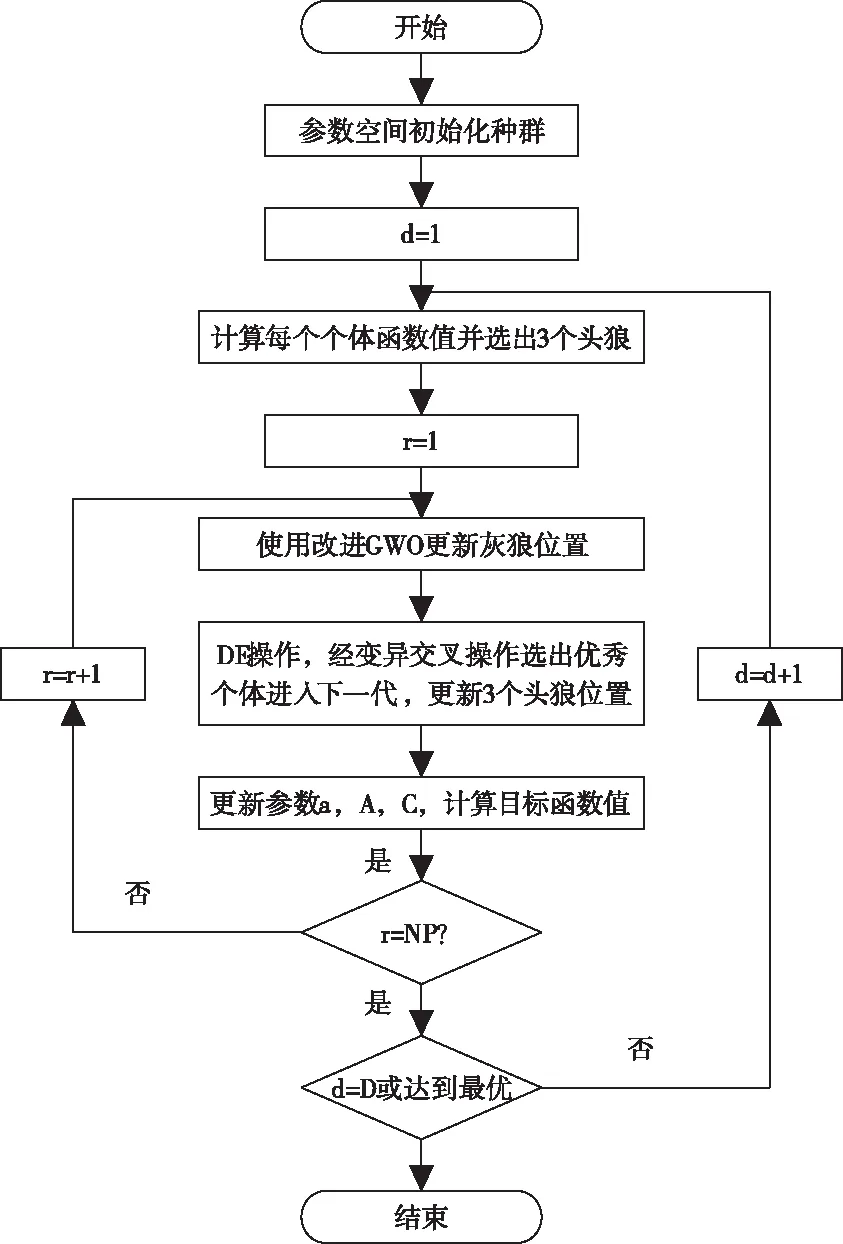
图2 DE-GWO算法流程图

2.1 改进的灰狼优化算法

灰狼优化算法根据狼群的社会等级制度，划分为4种等级α、β、δ和γ，也就是最优解、次优解、季优解和候选解，并依据各等级进行猎物的搜寻、围捕和攻击。基于此，在搜索空间中利用表现最好的3个头狼在不断的迭代过程中在各自区域内寻找最优解可能的位置，以此引导来搜索全局最优解。该算法参数少、鲁棒性强，但收敛速度慢、容易陷入局部最优。

原始的灰狼优化算法(GWO)数学模型[4]如下：计算3个头狼与猎物之间的位置

Dα=|C1.Xα-X|

(1)

Dβ=|C2.Xβ-X|

(2)

Dδ=|C3.Xδ-X|

(3)

C=2ar2

(4)

再计算当前解的最终位置

X1=Xα-A1Dα

(5)

X2=Xβ-A2Dβ

(6)

X3=Xδ-A3Dδ

(7)

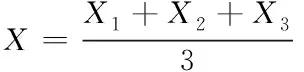
(8)

A=2ar1-a

(9)

其中X为猎物也就是目标解，D为每个头狼与猎物之间的距离，r1、r2为0到1之间的随机值，a随着迭代次数从2线性减小至0。本文考虑到式(8)产生解并不一定为最优解，使用贪心算法将式(5)～(8)都当作候选解，根据计算适应度函数值，选择适应度函数最低的解为当前最优解。

而由于原始算法在前期搜索过程中过于依赖三个头狼的带领，为了增加算法前期全局开采能力，本文使用一种分段搜索的方法，以|A|=1为临界值，若|A|≥1，则按原算法进行位置更新，若|A|<1，则使用以下公式进行距离的计算

D1=|C1.Xα-Xb|

(10)

D2=|C2.Xb-Xc|

(11)

D3=|C3.Xc-Xα|

(12)

其中Xb、Xc为种群中随机的两个个体，Xα依旧是最优秀的头狼。通过上述公式将前期搜索范围扩大到当前最优个体和随机2个个体共同决定的圆形区域内，既增强了全局搜索能力，也因为当前最优解在区域内，保证了不会进行盲目搜索。再通过式(5)～(8)进行位置更新生成4个候选解进行比较生成当前最优解。

算法主要步骤如下：1)设置灰狼种群规模N、迭代次数t、空间维数d，搜索空间上界ub与下界lb；2)参数空间随机初始化种群并计算适应度函数值；3)依据适应度函数值找出3个最优个体，分别为Xα、Xβ、Xδ；4)通过分段搜索策略和贪心法则更新种群位置并更新参数a、A、C。

2.2 改进的差分进化算法

差分进化算法(DE)因其优秀的寻优能力，常常与其它算法进行结合提升原算法的优化能力，本文将差分进化算法引入到灰狼优化算法中，解决了GWO算法在前期易早熟的缺点，同时具备了前期较强的搜索能力和后期不错的寻优能力。

总之，工作坊教学模式以学生为主体、教师为主导，注重学生应用能力培养，契合了应用型高校大学生培养注重知识运用、实践技能、创新能力、综合素质的要求。食品科学与工程专业尤其注重学生的应用能力，工作坊教学模式在果蔬加工工艺学课程教学中的应用表明这种模式适宜在食品科学与工程专业相关课程教学中推广。

原始的差分进化变异方式为

V=X1+F(X2-X3)

(13)

为了提高前期搜索速度与全局搜索性和后期收敛速度，本文参考FAN的方法[12]并做出修改使用一种新的变异操作为

V=X1+F1(Xα-X1)+F2(X2-X3)

(14)

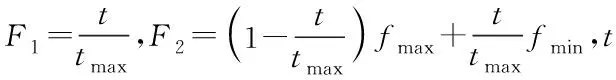
2.3 ICP优化算法

点云配准在不考虑形变扭曲的情况下，本质就是计算2个视角下点云数据的刚体变换矩阵(RT矩阵)，而配准过程中，ICP算法是公认效果最好的，但在实际情况中，传统ICP算法配准往往会因为配准数据量过大而配准速度缓慢，另外若初始位置相差较大，很容易陷入局部最优甚至导致配准失败针对这两个问题，本文在前期使用k-d tree[13]二叉树法进行点对之间快速搜索，具体步骤为：①将搜索节点与分裂值节点比较，若小于分裂值则转入左子树分支进行比较，否则转入右子树分支比较；②“回溯操作”，对其它分支子空间进行搜索，若有更近点，则跳入子空间；③重复以上操作，将各分支搜索完之后输出最近邻点和距离。

其次，为了降低噪声点对参数计算的影响，本文加入距离限制，设定阈值ε，将点对之间欧式距离大于阈值的点对当作噪声点进行剔除。

2.4 DE-GWO+ICP两步配准算法

在三维重建领域中，针对不同视角点云..不同视角点云的配准问题一直是重点和难点，为解决传统ICP算法配准速度慢且对初始位置要求高等问题，本文提出一种改进的点云配准方法，在粗配准中使用改进的DE-GWO算法为细配准提供良好初值，后续精细配准中使用ICP优化算法，使用此方法对配准过程进行优化，同时提升了配准的速度和精度。改进后的DE-GWO+ICP算法具体步骤如下：

Step2：使用k-d tree二叉树进行近邻点搜索并进行噪声点剔除。

Step3：初始化DE-GWO参数，将RT矩阵中的3个旋转角和3个平移量分别进行编码作为DE-GWO算法的个体X，再将点云配准的均方根误差作为算法的适应度函数，即

(15)

其中pi为原点云中的点，qi为配准点云当中的点。

Step4：使用DE-GWO算法进行迭代更新，计算每次迭代最优个体适应度，若达到配准要求精度，或达到迭代次数，则算法停止并输出点云集作为ICP算法的初始数据，否则重复操作。

Step5：使用ICP优化算法进行点云精细配准，若误差小于给定阈值，则两片点云进行匹配，否则重复操作。

3 实验结果与分析

实验平台为Matlab R2018a，CPU使用Intel(R) core(TM) i5-8300，8 G内存，Windows10系统。实验模型为斯坦福大学提供ply格式的标准模型[15]，选用bunny、dragon和buhhda数据模型作为实验对象。

首先设置算法各参数，为保证一般性，设置种群规模NP=40，迭代次数60，缩放因子最大值0.6，最小值0.2，CR为0.8，剔除噪声点阈值为0.001。对粗配准中改进DE-GWO算法进行收敛性分析，对bunny模型进行配准实验，观察每次迭代后适应度函数最优值，每种算法运行30次取平均值，如图3所示，可以看到改进DE-GWO算法相比于原始的DE算法和GWO算法，收敛速度有了明显的提高，验证了改进算法的有效性。

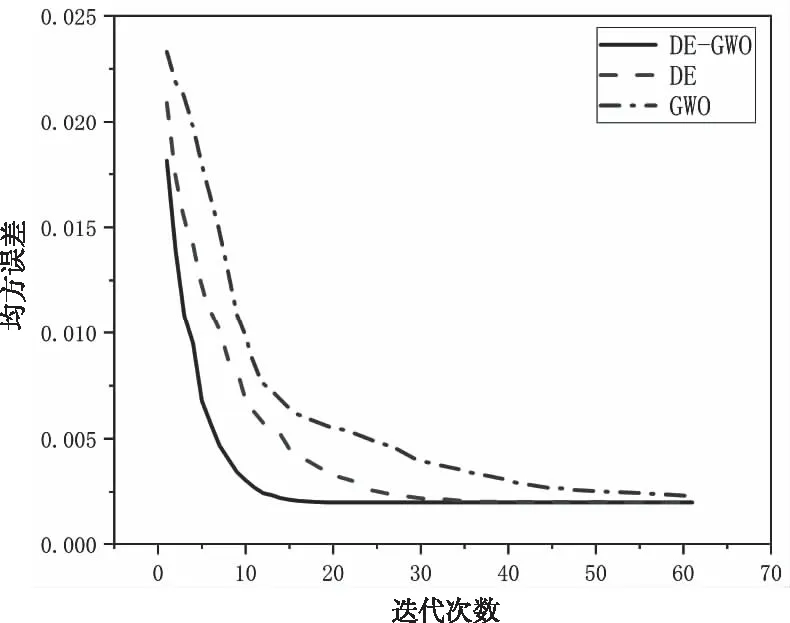
图3 三种不同算法收敛曲线

然后使用传统ICP算法和本文改进后的配准算法分别对bunny、dragon和buddha点云模型进行配准实验，为了证明算法有效性，加入了在传统粗配准中使用的RANSAC(随机抽样一致性)算法和粗细配准结合的算法进行实验。配准实验效果图如下图所示。

图4 Bunny模型配准

图5 Dragon模型配准

图6 Buhhda模型配准

对比上图可知，改进后的配准算法无论是相比传统的RANSAC算法，ICP算法亦或是两者结合后的算法，配准效果都更加优越，使用改进的配准算法可以使两片点云达到近乎重合的效果。

其次对三组模型的配准过程进行配准时间记录和误差分析，误差计算使用文献[16]的方法，误差参数为：

(16)

(17)

其中δ为给定精度，文中取0.001，d(pi，qi)为两片点云中点对配准之后的距离。两种配准方法配准时间和误差对比如表1所示。

表1对比数据看出，RANSAC粗配准虽然时间迅速，但配准效果很差，ICP算法配准时间相对太长，且误差依然较大，两者相结合之后在时间和精度都有所提高，但仍旧不理想，尤其在Dragon模型上相比ICP算法并没有太多提高。而在前期粗配准中使用改进后的DE-GWO算法，在配准时间上相比传统ICP算法有了大幅度的提高，相比粗细配准结合的方法，无论速度还是精度上都更加优越。接着在粗配准后再使用ICP优化算法进行细配准，可以使配准误差有了更近一步的减少，表中Bunny模型误差再次减少了25%，Dragon模型误差再次减少了45%，Buddha模型误差再次减少了46%。综上。通过对比传统ICP算法和本文提出的改进配准算法对相同模型配准后的数据分析，本文提出的DE-GWO+ICP算法无论在配准速度还是在配准精度上都相比于传统ICP算法有了明显的提高。

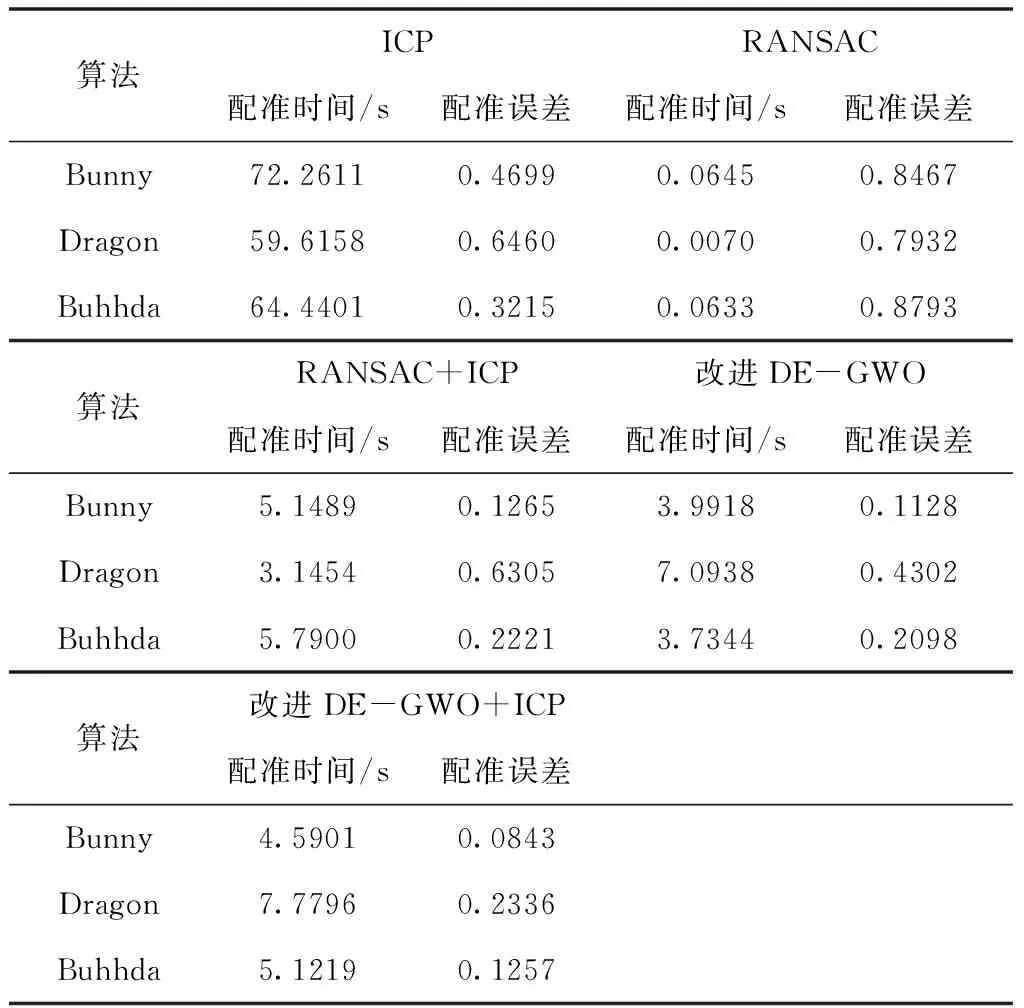
表1 不同算法配准时间与误差

4 结论

本文为解决原始灰狼优化算法易早熟收敛的问题，将差分进化算法引入原算法中，并采用一种新的变异方式进行变异更新，加快了算法的收敛性和解的精度。然后将算法引用于点云配准过程的粗配准中结合ICP算法产生一种新的配准方法，利用DE-GWO算法进行粗配准为精细配准提供了良好的初值，解决了ICP算法在实际点云配准过程中速度较慢且对初始位置要求过高等问题。通过对不同点云模型进行实验对比可知，改进算法对比原算法拥有更快的收敛速度和更好的寻优能力，且经过配准时间误差分析后，本文提出的算法相比传统ICP算法配准精度更高，配准速度更快，为三维重建过程中后续的点云表面重建工作提供了实践基础。