基于Workbench纤维增强扁挤压筒结构优化设计

吕树婷，成小乐,,王艳辉,，彭 耀

(1.西安工程大学 机电工程学院，陕西 西安 710048;2.北京理工大学 机械与车辆学院，北京 100081)

0 前言

现今，轨道交通、汽车、航空航天等方面实行轻量化发展，因此对轻合金型材的需求大大增加。实现轻量化方法之中行之有效的一种是将轻合金型材与中空结构型材设置为车身内壁结构，减轻车身重量[1]。挤压生产方法是轻合金型材的主要生产方式，而金属挤压机是实现金属挤压加工的核心设备，挤压筒作为金属挤压机的核心部件成本昂贵[2]。挤压筒分为圆筒和扁筒两类，在挤压力相同的条件下，扁挤压筒可以更好地代替圆挤压筒生产大型材[3]。扁挤压筒由于与型材具有几何上的相似性可以大大降低挤压力，提高金属流动的均匀性，但是由于扁挤压筒几何上的不完全对称性，在内衬处易形成应力集中，造成扁挤压筒的应力开裂失效[4-6]。现已有的研究大多倾向于碳化硅颗粒整体增强金属基复合材料，然而从材料的实际服役状态来看，材料的局部区域性能(如硬度、强度、耐磨性)往往对构件的服役寿命起着关键性作用。因此，很多工况下真正需要的仅仅是提高服役构件局部区域的性能，而非整个增强金属基复合材料。而且国内外现在针对扁挤压筒的优化目的基本上都是为了缓解应力集中。本文采用一种局部应力增强的方式，即在扁挤压筒容易产生应力集中的位置植入碳化硅纤维，使得纤维来抵抗受力过程中产生的拉应力，从而达到优化目的。

1 扁挤压筒有限元模型及参数选择

1.1 模型参数选择原则

本文采用在绘图软件上建立四分之一模型，并且在整个模拟过程中不考虑扁挤压筒实际工作中会有的各种情况，比如材料的不均匀性、温度在整个过程中各部分的不均性、和本身材料的小缺陷等产生的影响。并在此基础上进一步作出如下假设[7-10]：

(1)工作内压为等静压，均匀分布在扁挤压筒内孔上;

(2)扁挤压筒每层采用的材料相同，且弹性模量和泊松比相同；

(3)内衬和外套之间不会产生任何位移变化；

(4)扁挤压筒各层衬套尺寸公差与设计参数一致；

针对5 MN挤压机用扁挤压筒，其力学模型如图1所示。其中a为内孔短半轴，a=40 mm，b为长半轴，初始长度为80 mm，r内衬外径，r=110 mm，R外套外径，R=220 mm。本文选取的是双层扁挤压筒，由前面的假设，各层材料都采用H13。引用5 MN扁挤压筒的优化参数见表1[11-12]。

图1 扁挤压筒力学模型示意图

表1 扁挤压筒力学模型参数

1.2 扁挤压筒的载荷与约束

用有限元软件做出1/4挤压筒的网格图如图2所示。并在其端面施加对称约束。因为扁挤压筒在工作时不允许z向产生位移，所以在前后端面上也应施加约束。在工作过程中，只考虑扁挤压筒内孔上的受力，并且假设全部受均布载荷作用，其模型如图2所示。内压P可按式(1)计算

图2 载荷及约束模型

(1)

式中，F为挤压机的挤压；r为挤压筒内孔横截面半径。

2 扁挤压筒结构优化设计

2.1 优化设计方案

扁挤压筒装配状态下应力峰值及应力分布均匀性都会影响其使用寿命。本章以5 MN 挤压机用扁挤压筒为例，探究设计过程中扁挤压筒的相对过盈量、层间径比两变量对扁挤压筒等效应力峰值的影响，以及对扁挤压筒应力分布均匀性的影响探究；另外探究在同样拉伸力下，加入碳化硅纤维后对初始材料的屈服强度和抗拉强度的影响。

根据扁挤压筒优化研究经验，对扁挤压筒的相对过盈量、层间径比的参数值进行优化。扁挤压筒初始相对过盈量为0.25%，外套外径为420 mm，椭圆度为1.0，应力应变云图如图3所示，最大装配应力出现在圆弧顶端，大小为713.61 MPa；

图3 初始参数应力应变云图

2.2 模拟结果与讨论

2.2.1 相对过盈量优化

分别对相对过盈量为0.21%、0.26%、0.31%、0.36%及0.40% 时的扁挤压筒装配及工作应力分布进行模拟分析。装配过盈量与装配应力及工作应力关系见图4。当扁挤压筒的相对过盈量为0.26% 时应力分布如图5所示，在孔的圆弧顶端处会出现扁挤压筒的最大装配应力，大小为706.88 MPa；扁挤压筒最大工作应力为1 207.9 MPa。由应力云图可以看到内衬应力最大位置都在内孔上，并且向外表面不断下降，内孔表面发生的装配应力变化是向直线段不断降低。最小应力出现在工作孔两对称直线段附近，优化扁挤压筒相对过盈量后的工作应力峰值相比于初始结构，降低了10%。

图4 应力与相对过盈量关系图

图5 过盈量为0.26%时应力分布图

2.2.2 层间径比优化

分别对外套外径为400 mm、410 mm、420 mm、430 mm、440 mm、450 mm的扁挤压筒装配及工作应力分布进行模拟分析。扁挤压筒的层间径比与装配应力及工作应力关系如图6所示。当扁挤压筒的外套外径为440 mm时应力分布如图7所示。

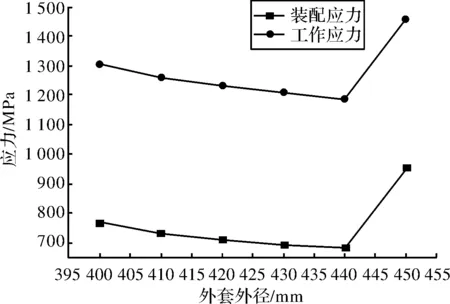
图6 应力与外套外径关系图

图7 外套外径为440mm时应力分布图

最大装配应力值在内衬孔圆弧与x轴交点位置附近取得，最大应力大小为682.77 MPa，最大工作应力为1 185.1 MPa，由应力云图可以看到内衬应力最大位置都在内孔上，并且向外表面不断下降，内孔表面发生的装配应力变化是向直线段不断降低。最小应力出现在工作孔两对称直线段附近，优化扁挤压筒相对过盈量后的工作应力峰值相比于初始结构，降低了9%。

3 Workbench拉伸模拟

本章所采取的模型主要是在先前的优化方案基础上选取最优，即相对过盈量为0.26%，外套外径为440 mm，椭圆度为1.0的扁挤压筒模型。在此时扁挤压筒的应力集中位置取块，并植入碳化硅纤维，观察抗拉强度、屈服强度以及应变的变化。

3.1 碳化硅纤维

SiC增强金属基复合材料会明显提高基体材料的综合力学性能，如比强度、比刚度[15]。并且使得原始基体材料的使用温度提高200℃左右。经查阅，碳化硅纤维的化学成分含量见表2。

表2 SiC纤维各项物理参数

3.2 碳化硅纤维与基体材料配合方式

本文中拉伸测试的前提是将碳化硅纤维通过纤维-基体-纤维的配合方式加入基体材料，基体材料采用的是H13(4Cr5MoSiV1)，这是因为碳化硅纤维在作为金属基的增强体时，使得金属材料本身的导电导热性能和热膨胀系数都很小，可以保证尺寸精度波动小。拉伸试样加工成长度为 23 mm，最大半径为Φ8 mm的标准拉伸试样体，试样的具体尺寸见图8 。

图8 拉伸试样结构示意图

将建好的模型直接导入Workbench工作空间，设置好材料属性和约束等进行拉伸实验，从而获取屈服强度YS、抗拉伸强度UTS。观察碳化硅纤维的嵌入是否对基体材料区域各项力学性能有所改善。

本文中所采用的材料为H13模具钢，将原始柱体材料中间打长55 mm、厚度为1 mm的通孔，并且嵌入碳化硅纤维层来代替通孔的原始材料，其结构模型见图9。

图9 配合材料结构模型示意图

3.2.1 基体材料拉伸测试

设定初始基体材料的抗拉强度为2 040 MPa,屈服强度为1 460 MPa，初始应变为0.99×10-2，拉伸后的应力应变结果见图10，应力应变最大位置都出现在试样中部，所以断裂位置也发生在试样中部。

图10 初始屈服和抗拉强度应力云图

3.2.2 基体-纤维-基体配合拉伸测试

采用与初始基体同样的拉伸力来加压，配合材料的屈服强度、抗拉强度的应力图如图11 所示。同样，应力和应变最大位置也都出现在试样中部。

图11 配合材料屈服和抗拉强度应力云图

从两个模拟结果的对比来看，加入纤维的材料屈服时最大应力为1 312.8 MPa，抗拉强度下最大应力为1 833.6 MPa。本着最大应力接近于材料屈服/抗拉强度的原则，同样的拉伸力下，配合材料比基体材料的屈服强度提高了11%；抗拉强度提高了11%；由应变云图可以看出材料内部的变形比初始发生了改变，并且由拉伸后的长度发现延伸率并没有发生改变。符合了预期设想，证明了碳化硅纤维的加入确实提高了初始基体材料的各项性能。

4 结束语

(1)通过本文的研究，表明所研究的优化方向是正确的，并且由结果可知确实起到了优化效果；最佳的相对过盈量选取在2.75%左右，在合适的相对过盈量下，最大等效应力减小明显。

(2)模拟结果显示，改变外套外径和椭圆度两因素时，在外套外径为440 mm，椭圆度为1.0时，分别取得了最佳应力分布和最小装配/工作应力。

(3)通过拉伸模拟仿真结果，发现加入碳化硅纤维确实增强了初始基体材料的部分性能，在最终拉伸结果图上，显示加入碳化硅纤维后材料的屈服强度和抗拉强度都比初始基体材料增加了11%。