宽厚板四点弯曲压力矫平理论建模与有限元分析

陈亚飞，杨若雯，俞洪杰，魏鹏洋，江连运

(1.太原科技大学 机械工程学院，山西 太原 030024；2.中国重型机械研究院股份公司，陕西 西安 710018；3.太钢不锈钢股份有限公司不锈热轧厂，山西 太原 030024)

0 前言

高强宽厚板在现代工业化时代需求旺盛，其广泛应用于重型装备、压力容器、国防军工等重点工程领域，对国民经济的快速发展和生产技术的进步起着不可代替的作用[1-2]。然而，宽厚板在经过轧制、热处理等过程后可能会出现不同程度的弯曲[3]，因此，为提高板材的平直度，需要对出现不同程度的板形缺陷进行压平或矫直。

平直度作为宽厚板的重要质量指标，一直是轧制技术攻关的重点与难点[4-5]。对于宽厚板的矫平过程，目前国内传统的是通过压力矫平，即人工设定压头的行程、人工放置垫板、人工通过仪器测量板材的残余挠度等，严重影响板材的矫直效率及精度，与全自动化压力矫平过程的发展趋势相悖。同时由于三点弯曲矫直工艺具有其局限性，矫直次数较多，效率低[6]，并且当跨距较大时，矫直精度相对较差。基于此，本文针对宽厚板四点弯曲压力矫平特点建立相关理论模型，并利用有限元模拟进行验证，这对全自动、高精度压力矫平过程的实现具有重要的现实意义。

随着工业生产的发展，人们对宽厚板平直度的要求逐渐提高，矫直工艺过程中提高压平机的矫直精度和效率已成为亟待解决的问题。为此，国内外诸多学者进行了相关研究。Lu H等[7]通过曲率变化相关理论推导出了工件初始挠度和矫直行程之间的关系，并进行相关实验验证了理论计算的准确性；魏钦玉等[8]建立了金属棒材四点弯曲压力矫直行程预测模型，结果表明，与三点弯曲压力矫直方案相比，采用双压头双支撑结构的四点弯曲压力矫直方案在精度和工件变形上均具有明显的优势；候海涛[9]研究了多点反弯矫直模型中各参数对反弯量的影响，拟合出多项式形式的反弯量计算公式，并基于ABAQUS软件制定了不同曲率特征钢板的矫直方案；PEI Y C等[10]建立了D型截面轴弯曲矫直预测模型，并通过实验研究和对比分析，验证了该模型的正确性；Timothy J B等[11]模拟了钛合金板带材张力作用下连续弯曲矫直过程，并建立了该工艺下表层应变计算模型；江连运等[12]建立了宽厚板三点弯曲压力矫平数学模型，并采用有限元模拟了各种工况下宽厚板的压力矫平过程，证实了理论模型的准确性。

由于宽厚板压力矫平过程也涉及到回弹问题，针对材料的回弹问题国内外学者也进行了研究。张超等[13]建立了钢-铝复合板曲率积分模型并解析了其辊式矫直过程，结果表明，矫后钢-铝复合板覆层发生反向屈服，反向屈服会削弱复合板的回弹，且具有累积效应；李佼佼等[14]建立了三点弯曲有限元模型，模拟研究了不同厚度、不同温度下Invar 36合金厚板的回弹规律，并进行相关回弹试验，结果表明，该模型可有效预测不同工况下的回弹情况；Radha K L等[15]研究了板材成形过程中各因素对板材回弹的影响情况，并得到了最佳成形工艺参数；谢雨洁[16]针对型材中槽钢的弯曲成形问题，采用三点弯曲和四点弯曲建立压模，并进行有限元模拟得到了该槽钢的回弹量。由此看来，在“大数据/AI”、“智慧工厂”的时代背景下，目前还缺少一种宽厚板四点弯曲压力矫平理论模型用于指导生产，以提高矫直精度和效率。

本文针对弯曲半径较大的板材，通过建立宽厚板四点弯曲压力矫平理论模型，可进一步提高板材矫直精度和效率，并采用有限元方法研究了板材平直度的影响机理，验证了模型的准确性；通过本文内容的研究，实现了工艺参数的精准设定和高效率压力矫平，为实际生产提供重要理论和技术支撑。

1 理论模型建模

根据宽厚板压力矫平四点弯曲变形的特点，在理论建模时进行如下假设：

(1)板材在弹塑性变形过程中，中性层位于板材厚度中心；

(2)板材在压力矫平过程中，其横断面变形后仍为平面；

(3)板材材料为双线性各向同性且均匀。

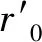
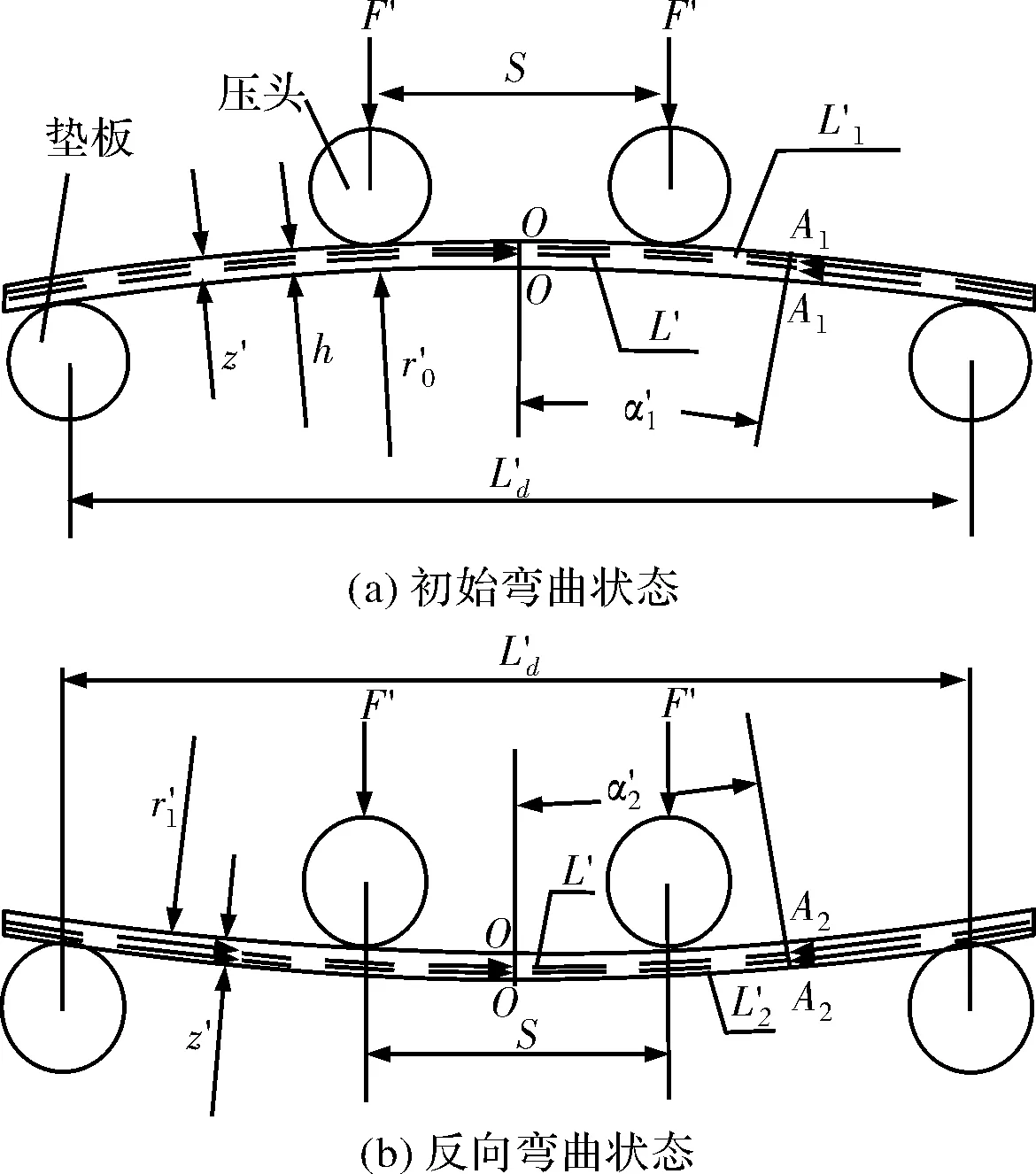
图1 板材弯曲状态

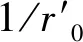
(1)

其中：

将其代入式(1)得到应变为

(2)

由式(2)可计算出板材弹性区临界层距中性层的高度为

(3)

式中，σs为屈服强度；E为弹性模量。

对于板材矩形截面，其外力矩M的表达式为

(4)

式中，w为板宽；h为板厚。

将式(3)代入式(4)，得到外力矩与曲率之间的表达式为

(5)

式中，Mw为最大弹性弯曲力矩，Mw=wh2σs/6；1/ρw为弯曲力矩为Mw时的曲率值，1/ρw=2σs/hE。

(6)

式中，I为截面惯性矩，I=wh3/12。

当弹复曲率等于反弯曲率时，板材才会弹性恢复到平直状态，实现压力矫平。因此，外力矩M与弹复力矩Mt相等，即

(7)

(8)

由图1中板材弯曲状态几何关系及三角定理，得到板材中心相对边部垫板的反弯量为

(9)

2 有限元分析及验证

2.1 四点弯曲压力矫平有限元模型

本文采用有限元软件模拟不同工况下板材的四点弯曲压力矫平过程，如图2所示。其中，压力矫平过程中可忽略上下垫板的弹性变形，将其设置为刚性体；板材设置为双线性各向同性材料，单元类型为solid164。板材的约束可通过上下垫板与板材之间的接触来实现。垫板与板材之间的静摩擦因数为0.3，动摩擦因数为0.25。材料力学性能参数如表1所示。

图2 四点弯曲压力矫平模型

表1 材料力学性能基本参数

在四点弯曲压力矫平过程中，压头可以沿竖直方向移动，压下速度为2 mm/s，压下行程根据式(9)计算的反弯量来确定。其中，压力矫平包含加载、保压和卸载三个过程。加载过程是缓慢的，需要设定一个加载时间，加载完成后开始保压，保压过程中压头不动，保压时间为10 s，之后卸载过程为压头回到初始位置，板材开始回弹。

2.2 四点弯曲压力矫平模型的验证

2.2.1 不同板宽下的理论模型验证

选用跨距为1200 mm、板厚为80 mm、屈服强度为235 MPa、弹性模量为200 GPa、初始挠度为22.53 mm、板宽分别为4 000 mm、3 000 mm和1 500 mm的弯曲板材。根据设定的边界条件和初始条件，利用建立的四点弯曲压力矫平理论模型将参数代入式(8)和式(9)计算出各自对应的压平力和反弯量，如表2所示。采用Ansys LS-DYNA模拟了各种对应工况下的压力矫平过程，得到的模拟结果如图3所示。

表2 载荷挠度表

图3 不同板宽下的压平结果

由图3得到的板材各个节点的位移和位置数据，对数据进行整理计算，获得了各种工况下的压力矫平后的板材平直度。其中，跨距为1 200 mm、板厚为80 mm、屈服强度为235 MPa、弹性模量为200 GPa、初始挠度为22.53 mm、板宽为4 000 mm的板材，压平后的平直度为3.8 mm/m；板宽为3 000 mm的板材，压平后的平直度为3.8 mm/m；板宽为1 500 mm的板材，压平后的平直度为3.8 mm/m。满足工业上在板厚大于25 mm、屈服强度小于460 MPa的情况下，板材的不平度小于7 mm/m。因此，通过有限元方法验证，不同板宽下的四点弯曲压力矫平理论模型合理可靠。

2.2.2 不同板厚下的理论模型验证

选用跨距为1 000 mm、板宽为1 500 mm、屈服强度为235 MPa、弹性模量为200 GPa、初始挠度为12.50 mm、板厚分别为80 mm、100 mm和120 mm的弯曲板材。根据设定的边界条件和初始条件，利用四点弯曲压力矫平理论模型,计算出各自对应的压平力和反弯量，如表3所示。采用Ansys LS-DYNA模拟了各种对应工况下的压力矫平过程，其结果如图4所示。

表3 载荷挠度表

图4 不同板厚下的压平结果

由图4得到的板材各个节点的位移和位置数据，对数据进行整理计算，得到各种工况下的压力矫平后的板材平直度。其中，跨距为1 000 mm、板宽为1 500 mm、屈服强度为235 MPa、弹性模量为200 GPa、初始挠度为12.50 mm、板厚为80 mm的板材，压平后的平直度为2.8 mm/m；板厚为100 mm的板材，压平后的平直度为2.5 mm/m；板厚为120 mm的板材，压平后的平直度为2.8 mm/m。满足工业上在板厚大于25 mm、屈服强度小于460 MPa的情况下，板材的不平度小于7 mm/m。该理论模型对不同板厚的板材平直度精度满足要求。

2.2.3 不同跨距下的理论模型验证

根据设定的边界条件和初始条件，选用板宽为1 500 mm、板厚为80 mm、屈服强度为690 MPa、弹性模量为200 GPa、初始挠度为16.00 mm、跨距分别为800 mm、1 000 mm和1 200 mm的弯曲板材。利用四点弯曲压力矫平理论模型计算得到各自对应的压平力和反弯量，如表4所示。其模拟结果如图5所示。

表4 载荷挠度表

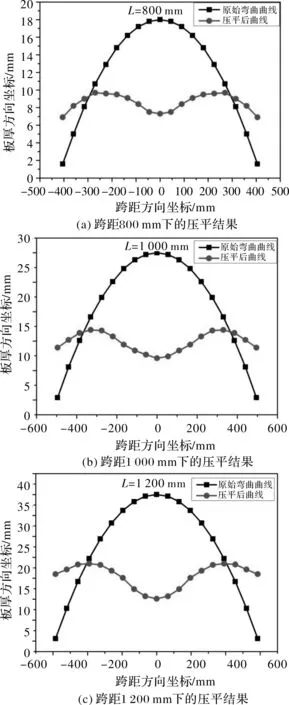
图5 不同跨距下的压平结果

板宽为1 500 mm、板厚为80 mm、屈服强度为690 MPa、弹性模量为200 GPa、初始挠度为16.00 mm、跨距为800 mm的板材，压平后的平直度为4.0 mm/m；跨距为1 000 mm的板材，压平后的平直度为4.8 mm/m；跨距为1 200 mm的板材，压平后的平直度为7.0 mm/m。满足工业上在板厚大于25 mm、屈服强度大于460 MPa的情况下，板材的不平度小于10.5 mm/m。由图5得到的板材各个节点的位移和位置数据。对数据进行整理计算，获得各种工况下的压力矫平后的板材平直度。

2.2.4 不同屈服强度下的理论模型验证

选用跨距为800 mm、板宽为1 500 mm、板厚为80 mm、弹性模量为200 GPa、初始挠度为16.00 mm、屈服强度分别为235 MPa、345 MPa和460 MPa的弯曲板材。根据设定的边界条件和初始条件，利用四点弯曲压力矫平理论模型计算得到各自对应的压平力和反弯量，如表5所示。模拟结果如图6所示。

表5 载荷挠度表

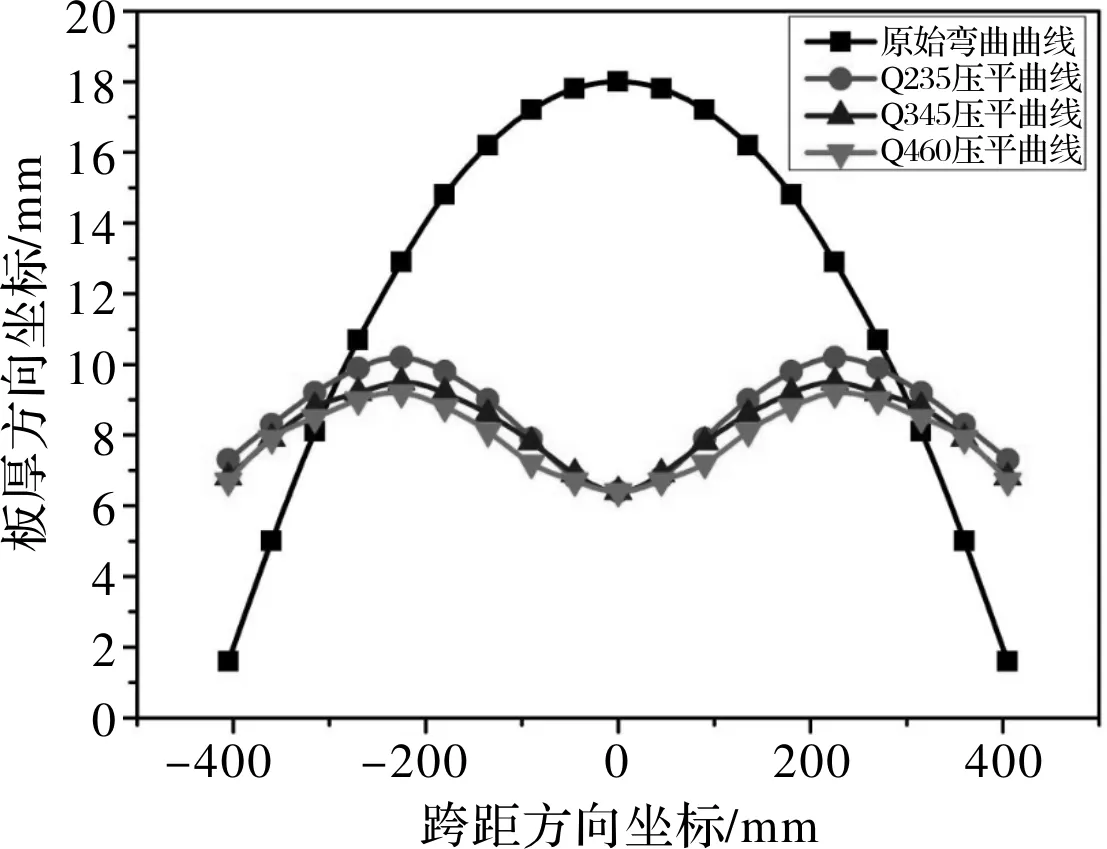
图6 不同屈服强度下的压平结果

跨距为800 mm、板宽为1 500 mm、板厚为80 mm、弹性模量为200 GPa、初始挠度为16.00 mm、屈服强度为235 MPa的板材，压平后的平直度为4.8 mm/m；屈服强度为345 MPa的板材，压平后的平直度为3.9 mm/m；屈服强度为460 MPa的板材，压平后的平直度为3.5 mm/m。满足工业上在板厚大于25 mm、屈服强度小于460 MPa的情况下，板材的不平度小于7 mm/m。由图6得到的板材各个节点的位移和位置数据，对数据进行整理计算，获得了各种工况下的压力矫平后的板材平直度。

3 结论

(1)针对弯曲半径较大的板材，提出四点弯曲压力矫平方案。运用弹塑性力学理论并结合压力矫平过程的特点，建立了宽厚板四点弯曲压力矫平理论模型；在材料力学性能参数和初始挠度等已知的情况下，可以计算出压平力和反弯量等参数。

(2)通过对不同板宽、板厚、跨距和屈服强度等工艺参数的设定，根据所建立模型计算出的反弯量采用有限元模拟压力矫平过程，计算得出了压平后板材的平直度。结果表明，各种工况均满足工业上宽厚板平直度要求，如在板厚大于25 mm、屈服强度小于460 MPa的情况下，板材的不平度均小于7 mm/m，验证了该模型的精度和可靠性。

(3)在“大数据/AI”、“智慧工厂”的时代背景下，建立的宽厚板四点弯曲压力矫平模型进一步提高了压平机的矫直精度和工作效率，为实现全自动压力矫平过程提供了重要的理论和技术支撑。