突发事件下相邻交叉口信号控制优化方法

陈 浩，韩 印，王嘉文，杭佳宇

（1 上海理工大学 管理学院，上海 200093；2 常州大学 机械与轨道交通学院，江苏 常州 213164）

0 引言

道路突发事件、如交通事故仍是普遍存在的［1］，特别是在高密度城市道路网络中超过50%的交通拥堵是由交通突发事件导致的［2］。如果突发事件发生在相邻交叉口、特别是短连线交叉口的连接路段，排队车辆会迅速溢流至上游交叉口，随着进入交叉口的车辆增多，车辆会溢出扩散到其他交叉口，并可能导致区域性交通拥堵［3］。事故区域也可能发生二次事故［4］。道路上的任何交通事故都有可能导致灾难性的交通堵塞［5］。这将间接导致时间资源的浪费［6］。因此，研究相邻交叉口事件发生后合理的信号控制策略对于缩短交通参与者行程时间的意外延误具有重要意义。

目前，城市道路交通事故的研究主要集中在紧急车辆的信号抢占紧急车辆（Emergency Vehicle，EV），可以挽救生命并减少财产损失。Qin 等人［7］提出了2 种EV 信号抢占控制策略。第一种策略中开发了一种实时控制方案，可以使信号从正常运行过渡到EVSP（EV signal pre-emption）；另一种控制策略通过优化算法，将信号从EVSP 转换回正常信号。Obrusník 等人［8］提出一种依赖于应急车辆和交通灯控制器之间的无线车辆到基础设施（Vehicle-To-Infrastructure，V2I）通信，该方法使激活时刻适应实际交通条件，使抢占时间尽可能短。Wu 等人［9］提出了一种EV 车道预清理策略，通过与周围联网车辆（Connected Vehicle，CV）的协同驾驶来优先考虑这些道路上的EV。

关于事故区域控制方面，许多学者也进行了研究。Long 等人［10］开发了4 种疏散控制策略，并展示了所提策略在双向矩形网格网络中分散基于事件的交通拥堵的有效性。Li 等人［11］提出了一种固定时间的信号边界控制，以缓解交通网络中的拥堵。Wang 等人［12］进一步分析了交通事故对车辆密度与效率性能关系的影响，提出了一种反馈边界控制策略方法，提高了车辆平均速度，并减少了受事件影响的交通的总延误。

综上，目前国内外学者积累了很多突发事件下交通信号优化策略的研究成果。然而，对车辆通过事件交叉口时通行效率的研究较少。同时，边界限流控制方法应对交通事故导致拥堵时，往往以全局最优为控制目标，不能精准调控强关联交叉口，且控制效果有延时。因此，有必要提出一种针对事件强关联交叉口的信号优化方法，迅速、精准应对交通事故。

为了弥补以上空白，本文主要做出以下2 点贡献：

（1）以可接受间隙理论为基础利用概率的方法，对突发事件下道路通行能力的公式进行了数学推导。

（2）建立了一个考虑事件的相邻交叉口信号优化模型，该模型适用于单车道的场景。为了对该模型进行求解，将蒙特卡洛方法引入遗传算法。

1 问题描述

在城市道路网络中，交通事故会对信号控制交叉口的运行性能产生影响。本文实现的具体场景如图1 所示。图1 为城市道路中一个两相位相邻交叉口，第一相位为东西方向通行，第二相位为南北方向通行。突发事件可能随机发生在相邻交叉口连接路段中的任意位置。事件发生后，由于是单车道，从上游交叉口驶入连接路段的车辆通过另一方向车道的车流间隙离开事故影响路段。为防止连接路段车辆溢流导致上游交叉口堵塞使拥堵扩散，不仅需要控制由上游交叉口A流向下游交叉口B方向的车辆，还要确保对向到达车辆排队队列长度，以满足车辆通过对向车道绕行通过事故区域。

图1 事件影响下相邻交叉口车辆运行机理Fig. 1 Vehicle operation mechanism at adjacent intersections under the influence of traffic incidents

根据不同的交通特征，常用的车头时距分布有负指数分布、移位负指数分布、M3 分布、Erlang 分布等。其中，负指数分布拟合单车道交通流车头时距分布时，较小的车头时距出现的概率大，与实际情况不符；移位负指数分布是在克服负指数分布局限性的基础上引入的分布函数，但该分布假定主路车辆是自由行驶的，与实际情况不符。由于连接路段发生突发事件，到达的车辆通过对向车道的车流间隙绕过事故路段。因此对向车道的车辆分布对交叉口运行效率影响更大。这里将进入相邻交叉口系统的车辆简化为固定的到达率。由于受到信号控制的影响，车辆到达停车线的车头时距用Cowan M3 分布来描述更符合实际［13-14］。

本文需做出如下假设：

（1）发生事故时，后方车辆在确保安全的情况下利用对向车道的车流间隙绕过事故区域，对向车道上行驶的车辆不受影响。

（2）经信号灯放行的对向车道车辆服从Cowan M3 分布。

2 信号优化模型

2.1 机动车延误模型

交叉口机动车平均信号控制延误模型，采用了美国交通研究委员会的《道路通行能力手册》中的延误计算方法。模型表述如下：

其中，为交叉口车辆的平均延误；d1为均匀延误；d2为增量延误；d3为初始排队延误；C为交叉口周期时长；gi为第i相位的有效绿灯时间；X为车道组的v／c比，也作饱和度；T为调查交叉口的观测时间；K、I为修正系数；qij为第i相位第j个进口道的车流量；c为车道组通行能力。

2.2 突发事件影响下通行能力公式

为了在突发事件下对相邻交叉口信号进行优化，本文以可接受间隙理论，引入概率的方法推导突发事件下通行能力公式。在对向车道上车辆服从Cowan M3 分布的条件下计算事件发生在连接路段后道路的通行能力。Cowan M3 的车头时距分布认为，当交通拥挤时，一部分车流以车队的状态行驶，而另一部分车辆以自由流状态行驶。分布函数如下：

其中，t为车头时距；τ为最小车头时距；α为自由流比例；λ为衰减参数，λ ＝

设p为满足（0，1）均匀分布的随机数，令p ＝F（t），代入后求得车头时距的反函数为：

由式（6）可得：

其中，ht，k为对向来车第k辆车的车头时距；pk为对向来车第k辆车的车头时距为ht，k的概率。在仿真过程中，计算得到的车头时距存在小于2 s 的情况，为了符合实际情况，将小于2 s 的车头时距修正为2 s，其他情况不变。

本文将车辆通过事件区域划分为2 种场景，分别是：对向车辆车头时距满足通过临界间隙时和对向车道没有车辆时，因此该路段一个周期内的通行能力即为周期时间内这2 段时间通过车辆数之和。在事故影响下一个周期内可以通过的车辆数为：

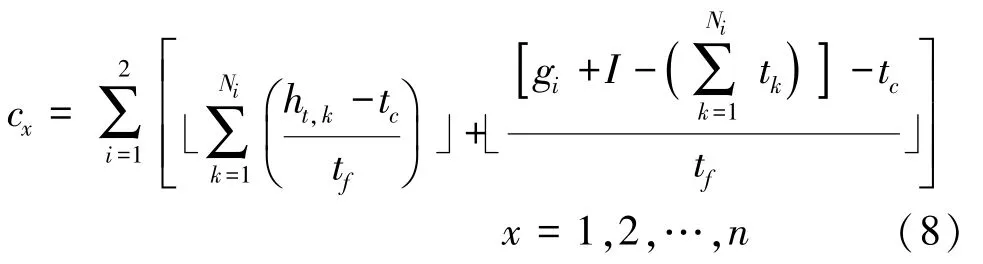
其中，N1、N2为对向车道第一、二相位分别到达的车辆数；tc为车辆穿越对向车流的临界间隙，该值需要根据事件的长度和宽度来确定；tf为绕行车辆以车队形式通过时的车头时距。

由于事故发生在连接路段，在一个周期内对向车道出现足够的时间间隙时都可以绕行通过事故地点驶向下游交叉口进口道停车线的位置。其中，为对向车道有来车时车辆之间车头时距间隙所能通过的车辆，判断了每一个车头时距间隙可通过的车辆并向下取整数。为对向车道、特别是车流量较小的情况，一个相位时间内对向车道来车已全部通过但相位仍未结束时车辆以车队形式通过事件地点的通行能力。

由公式可看出车辆通过事件地点的通行能力受到下游交叉口来车以及信号配时参数的影响。此时由公式（8）得到的是一次数值模拟的通行能力。本文在求解算法中引入蒙特卡洛方法，对该通行能力公式进行多次计算，得到通行能力的期望值。使用通行能力的期望值作为突发事件下车道折损后的通行能力进行信号配时参数的优化。则通行能力的期望值为：

其中，cx表示通行能力可能的取值；Px为cx对应发生的概率。

2.3 目标函数

延误是信号交叉口运行效率和服务水平的重要衡量指标，不仅反映了驾乘人员的舒适程度、受阻油耗和行驶时间损失，还反映了信号配时的合理性。因此，本文将进入相邻交叉口系统车辆的平均延误视为信号交叉口运行效率的度量指标。目标函数的定义如下式所示：

2.4 约束条件

（1）周期时长约束。上下游交叉口周期应介于最小、最大周期时长之间。计算公式具体如下：

其中，H为每相位启动损失时间；A为每相位黄灯时长；Ii为相位i的绿灯间隔时长。

（2）有效绿灯时长约束。最小绿灯时长应满足到达车辆能够驶离该交叉口。计算公式具体如下：

（3）排队长度约束。当相邻交叉口的连接路段发生事故时，通行能力会明显下降，受事故影响的连接路段会很拥挤，车辆会出现排队现象。为了防止车辆排队溢出影响到上游交叉口，还需添加约束控制连接路段双向车道的排队车辆长度。设L0为交通事故地点与上游交叉口之间的距离，单位为m；L1为交通事故后方排队车辆队列长度，单位为m；L2为发生事故车道对向车道停车线处排队车辆队列长度，单位为m。L1排队长度应小于L0，使事故地点后方排队车辆不会溢出至上游交叉口。事故车道对向车道车辆排队队列长度应小于L0-hs，使得对向车道预留出足够的空间给事故地点后方排队的车辆能够绕行。数学公式具体如下：

其中，qij，t、qij，r、qij，l分别为第i相位第j个进口道的直行、右转、左转车流量。

2.5 突发事件下相邻交叉口优化模型

至此，研究得到的突发事件下相邻交叉口优化模型可用如下数学公式进行描述：

3 优化算法

由于突发事件发生在道路上使得道路通行能力受到折损，且通行能力受到下游交叉口信号配时和交通量的影响将无法直接求解，因此本文将蒙特卡洛方法嵌入遗传算法中对其进行求解。蒙特卡洛方法也称统计模拟方法，是以概率统计理论为指导的一类非常重要的数值计算方法。蒙特卡洛方法的基本思想为：当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。

遗传算法直接对结构化问题进行操作，对目标函数的导数和连续性没有任何限制。其主要目标是在不同环境中使得在所需的效率和有效性之间取得平衡。因此，遗传算法在理论上或经验上不断得到改进开发以在复杂的解决方案空间中提供稳健的搜索。而且，由于遗传算法具有简单、易于实现、应用效果明显等优点，现已应用于模式识别、机器学习、组合优化等诸多领域。由于遗传算法是一种通用的优化算法框架，不依赖于任何具体问题，因此在城市交通信号控制的优化中也得到了广泛的应用。对于研发流程步骤，拟做阐释分述如下：

（1）初始化。设置进化迭代计数器为x ＝0，设置最大进化代数G，随机生成N个个体作为初始群体P（0）。

（2）根据随机生成的初始种群代入通行能力公式，进行多次求解，并取其期望值作为突发事件下影响的通行能力。

（3）个体评价。计算群体P（t）中各个个体的适应度。

（4）选择运算。将选择算子作用于群体，根据个体的适应度，按照一定的规则或方法，选择一些优良个体遗传到下一代群体。

（5）交叉运算。将交叉算子作用于群体。对选中的成对个体以某一概率交换个体之间的部分染色体，产生新的染色体。

（6）变异运算。将变异算子作用于群体。对选中的个体以某一概率改变某一个或一些基因值为其他的等位基因。

（7）循环操作。群体P（t）经过选择、交叉和变异运算之后得到下一代群体P（t ＋1），计算其适应度值。根据适应度值进行排序。准备进行下一次遗传操作。

（8）终止条件判断。若x≤G，则x ＝x ＋1，转到步骤（2）；若x ＞G，则此进化过程中所得到的具有最大适应度的个体作为最优解输出，终止计算。

4 仿真验证

4.1 通行能力模型验证

本节将对提出的交通事故下相邻交叉口车辆绕行通过事故区域的通行能力模型建立Vissim 仿真平台进行验证。并使用Matlab 对通行能力模型编程进行数值模拟。在相同环境的条件下，将计算得出的通行能力与Vissim 仿真中统计的通过车辆数进行对比分析。

由于Vissim 无法直接模拟车辆通过对向车道绕过事故区域的场景，因此需要进行一些特殊的处理。首先，将事故点处由西向东方向的车道与对向车道重合，设置好该条道路上车辆的路径。然后在该处设置冲突区域和让行规则。这时，若对向车道没有来车，到达的车辆就会直接行驶到重叠部分车道通过事故区域，若对向车道有来车，到达的车辆就会停下，待对向来车车头时距满足绕行的临界间隙或对向车道没有来车时择机通过。

在同一环境下进行Vissim 仿真时，设置5 组随机种子进行多次仿真，得出不同的迭代结果。实验的输入由下游交叉口驶入连接路段的交通量取不同的饱和度来计算连接路段事故点处的通行能力。上游交叉口的输入在确保不溢出的基础上尽可能大。如对向车道饱和度为0.3 时，上游流入下游车流输入值为812 veh／h 时发生了溢流导致交叉口堵死，因此适当减少车流输入值。并且只考虑了上下游交叉口流向连接路段的车流辆，分别为上游交叉口北进口道左转车流、南进口道右转车流、西进口道直行车流。下游交叉口分别为北进口道右转车流、南进口道左转车流、东进口道直行车流。并且假设左右转车辆比例分别为1 ∶3，其他方向车流直接驶出了该相邻交叉口系统，不影响连接路段的通行能力，因此不需要特殊考虑，只需要满足提出场景绿灯时间内能够通过即可。仿真使用的环境和车辆数见表1、表2，仿真结果见表3。

表1 交叉口信号配时Tab.1 Timing of intersection signals s

表2 交叉口流量Tab.2 Traffic volume at the intersection

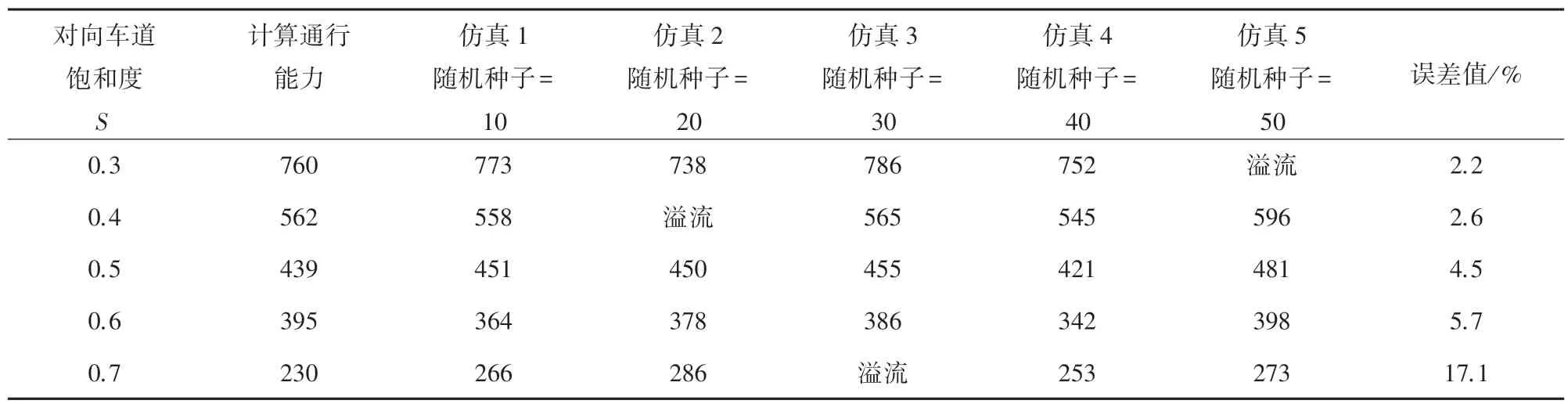
表3 实验结果对比Tab.3 Comparison of experimental results

由表3 可知，在相同的环境下，饱和度小于等于0.6时数值实验结果和仿真结果误差在可接受范围内。当路段发生事故、且对向车道车流量较大时，此时折损后的通行能力很难满足交通需求，使得相邻交叉口系统鲁棒性变差。对于连接路段车辆溢流堵塞上游交叉口的情况，一种可能的解释是这种场景下仿真通行能力小于计算通行能力的值，且差值较大。

4.2 信号优化模型验证

本节将对该优化方法进行数值实验，其中考虑了各种因素，以研究其对突发事件下相邻交叉口优化效果的影响。为了说明所提出模型的适用性。在本节中，对受到交通事故影响的两相位信号控制交叉口的信号配时进行优化。在数值模拟中，假设该相邻交叉口受到交通事故的影响。表4 总结了关键的参数取值［14］。

表4 关键参数取值Tab.4 Key parameters values

该验证场景中，东西方向为干线交通流，南北方向为非干线交通流。将本文所提出的方法与Webster 分为2 种情况进行讨论，分别是非干线交通量流量较低时（100 veh／h）与非干线交通量流量较高时（300 veh／h）两种场景下将干线交通逐渐增加进行数值模拟。在突发事件影响下利用通行能力公式进行验证表明在下游交叉口流向连接路段驶入上游车流饱和度超过0.6 时误差较大，因此在信号优化模型验证中没有考虑对向车道饱和度大于0.6 的情况。图2 显示了非干线车流在低流量状态下优化前后的效果。当非干线车流在低流量状态，主线车流从100 到400 之间时，优化没有明显效果。但是当主干线车流量增加到500 时，优化效果显著。

图2 非干线车流流量低时优化前后车辆平均延误Fig. 2 Average delay of vehicles before and after optimization when non-arterial traffic flow is low

图3 显示了非干线车流在高流量状态下优化前后的效果。当非干线车流大，干线车流从100 到200 之间时，优化没有明显效果。但当干线车流从300 到500 之间时，优化效果显著提高，相邻交叉口系统内的车辆的平均延误有明显的降低。此时，将优化结果代入得到各路段的饱和度，各路段饱和度均大于或接近0.5。

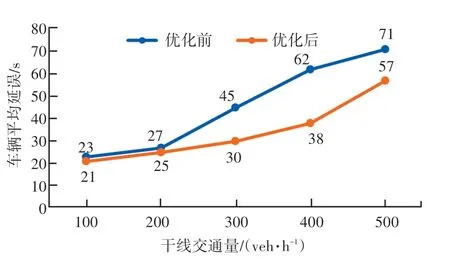
图3 非干线车流流量高时优化前后车辆平均延误Fig. 3 Average delay of vehicles before and after optimization when non-arterial traffic flow is high

对优化结果进行分析，对于交通流饱和度较低（s≤0.5）的交叉口系统，受到事件影响通行能力出现折损时，折损后道路的通行能力仍能满足需求，交通事故对交叉口整体运行效率影响有限，原有信号控制方案仍能发挥作用，所以此时优化效果不明显。而对于交通流饱和度较高（s ＞0.5）的交叉口信号控制的鲁棒性变差了。当受到交通事故影响通行能力出现折损时，路段的饱和度会很快达到饱和或者过饱和，导致原有的信号控制方案失效。因此，这时对该信号交叉口系统信号控制进行优化使得该交叉口系统整体的运行效率得到明显提升，车辆通过该交叉口系统的平均延误明显降低。对于非干线车流量小的情景，当干线交通量达到500 veh／h 时，车均延误降低了27%。当非干线车流量大时，干线交通量从300 增加到500，车均延误分别降低了33%、37%、20%。

5 结束语

本文提出了一种相邻交叉口信号配时协同优化方法，该方法考虑了相邻交叉口连接路段发生突发事件下的影响，使得进入该相邻交叉口系统的车辆因突发事件造成的行程时间意外延误显著减少。并通过模型仿真和数值分析验证了该方法的有效性。本次研究得出以下结论：

（1）对提出的通行能力模型搭建仿真平台验证发现，该研究场景下通行能力很大程度上受到下游交叉口的信号配时和下游驶入连接路段的车流量的影响。当下游驶向上游连接路段饱和度小于0.6时，提出的模型计算结果较准确。

（2）对提出的信号优化模型进行了数值模拟，发现交通流饱和度较高的相邻交叉口系统受到道路突发事件的影响通行能力出现折损，路段的饱和度会很快达到饱和或者过饱和导致原有的信号控制方案控制效果不理想，此时本文所提出的方案优化效果显著。