雪荷载作用下几字型钢日光温室极限承载力分析

王 聪，姜迎春，徐占洋，张 峰，白义奎，王铁良

·农业生物环境与能源工程·

雪荷载作用下几字型钢日光温室极限承载力分析

王 聪1，姜迎春2，徐占洋1，张 峰1，白义奎1，王铁良1※

（1. 沈阳农业大学水利学院，沈阳 110866；2. 沈阳农业大学工程学院，沈阳 110866）

雪灾是导致日光温室倒塌的主要原因之一。为探明几字型钢日光温室在雪荷载作用下的失稳机理，该研究采用有限单元法，以8 m跨日光温室为研究对象，模拟其在雪荷载（均匀分布雪荷载和非均匀分布雪荷载）作用下的失稳破坏过程，计算其极限承载力，并探究纵向系杆、初始几何缺陷、截面参数对极限承载力的影响。结果表明：对于净截面面积、上翼缘宽度、腹板高度和壁厚均相同的几字型钢和空心矩形钢管，几字型钢日光温室极限承载力稍高于空心矩形钢管日光温室极限承载力；相较于均匀分布雪荷载，日光温室拱架对非均匀分布雪荷载更为敏感，非均匀分布雪荷载作用下的极限承载力约是均匀分布雪荷载作用下的28%，在日光温室结构设计中，应重点考虑非均匀分布雪荷载工况；在非均匀分布雪荷载作用下，屋脊和后屋面支座处为危险截面，最先进入全截面屈服状态；纵向系杆的设置可有效抑制结构平面外变形，进而提高结构极限承载力，有纵向系杆约束条件下的结构极限承载力约是无纵向系杆约束条件下的1.25倍；该日光温室拱架对初始几何缺陷敏感度较低，当最大初始几何缺陷幅值从5 mm增加到20 mm时，极限承载力降低约2%；在几字型钢截面选取时，在满足规范要求宽厚比前提下，建议上翼缘宽度与翻边宽度之比控制在4.17左右，腹板高度与翻边宽度之比不大于9.25，下翼缘宽度与翻边宽度之比不大于1.7，上翼缘宽度与下翼缘宽度之比控制在3.33左右，腹板高度与下翼缘宽度之比控制在4.67左右。该研究结果可为开口冷弯薄壁型钢日光温室拱架抗雪设计提供参考。

温室；承载力；荷载；有限单元法；失稳破坏；冷弯薄壁型钢；开口截面；截面优化

0 引 言

日光温室是一种具有中国特色、拥有自主知识产权的设施类型，具有结构简单、节约能源、经济效益相对较高等优点[1]。作为一种农业建筑，其不仅要给植物提供适宜的生长环境，还需具有抵抗风雪等外部荷载的能力[2]。雪灾是北方地区主要气象灾害之一，2021年11月，辽宁出现特大暴雪天气，造成大量日光温室倒塌。从调查结果来看，日光温室结构失效模式主要为失稳破坏[3]。因此，了解日光温室结构在雪荷载作用下的失稳机理，对于提高日光温室结构抗雪灾能力具有重要意义。

从日光温室骨架形式来看，目前主要流行2种结构形式：桁架结构和单管结构。桁架结构将构件的内力转化为杆件的轴力，提高了截面的利用效率，在承载能力方面具有显著优势[4]。目前，国内学者针对桁架结构日光温室的稳定性能[5-7]，结构优化[8-10]，节点设计[11]和动力响应[12-13]等方面进行了较多研究，这些研究结果为桁架结构日光温室应用与推广提供了理论依据。然而，桁架结构存在用钢量大、标准化程度低、抗腐蚀性能差、焊接工作量大且质量不易保证等缺点。

近年来，随着日光温室结构向轻简化、装配化的方向发展，单管结构日光温室逐步开始发展并越来越多的应用在实际工程中[14-15]。相较于桁架结构，单管结构具有用钢量少、标准化程度高、抗腐蚀性能好、安装方便等优点。目前，针对单管结构日光温室受力性能的研究主要有：齐飞等[16]采用“全荷载组合”对平椭圆管日光温室拱架进行结构分析；丁敏等[17-18]研究了覆盖材料蒙皮效应对方管日光温室整体稳定性能的影响；闫冬梅等[19]运用3D3S软件研究了拉杆布置位置对椭圆管日光温室拱架内力分布的影响，并建议在不设置屋脊拉杆情况下，尽量把屋脊做成圆弧形；针对单管骨架截面刚度和强度较低等问题，齐飞等[20-21]基于临时加固策略研究了前屋面竖向支撑对温室骨架安全性能的影响，并给出了支撑数量和支撑位置的建议值。Wang等[22-24]运用ANSYS软件对装配落地式单管日光温室拱架进行静力特性与动力时程分析。白义奎等[25]对平椭圆单管日光温室进行全尺寸加载试验。以上研究成果为单管结构日光温室防灾减灾和应用推广提供了理论依据。

值得指出的是，以上研究仅限于闭口截面的方管、矩形管或平椭圆管。相较于闭口截面钢管，冷弯薄壁开口截面型钢（如几字型钢）具有加工成本较低、制作工艺简单、材料利用率较高等特点。因此，其在实际工程中得到广泛应用[26-28]。然而，由于开口截面属性，几字型钢构件抗扭能力弱，截面形心与剪心不重合，在竖向雪荷载作用下易发生失稳破坏[29]。因此，探究几字型钢日光温室拱架在雪荷载作用下的失稳机理，计算其极限承载力，对于提高其抗雪灾能力具有重要意义。

为此，本研究以几字型钢日光温室拱架为研究对象，采用ANSYS有限元分析软件，模拟其在雪荷载作用下的失稳破坏过程，分析其破坏模式，计算其极限承载力，并探究纵向系杆、初始几何缺陷、截面参数对极限承载力的影响，从而寻求最优截面尺寸参数，为几字型钢日光温室结构抗雪设计提供参考。

1 温室结构参数

本文选取某跨度为8 m，脊高为3.8 m的日光温室为研究对象，具体结构参数如图1所示。前屋面水平投影6.5 m，后屋面水平投影1.5 m，后墙高2.3 m，后屋面角45°。为保证日光温室整体稳定性，在前屋面和屋脊处布置4道纵向系杆。温室前后屋面拱架选用（××××）50 mm×70 mm×15 mm×12 mm×2 mm冷弯薄壁几字型钢，截面尺寸如图2所示。

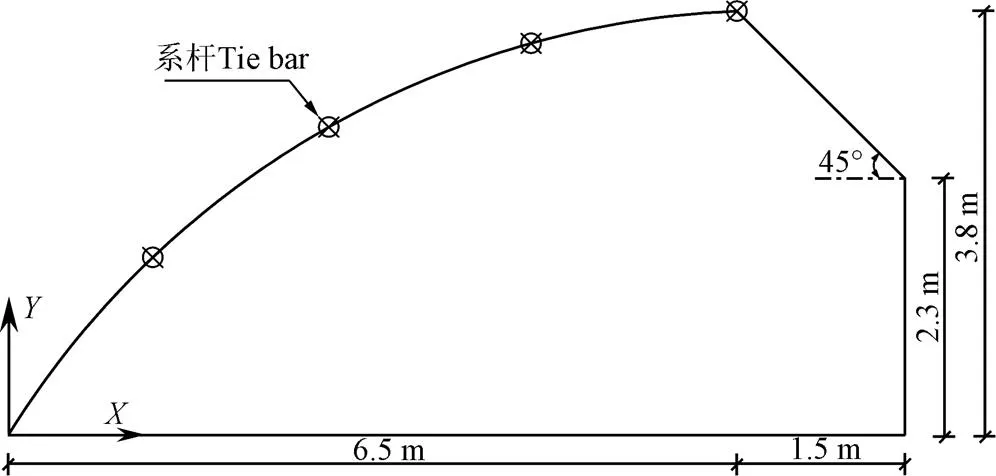
图1 日光温室剖面示意图

注：a为下翼缘宽度，mm；b为上翼缘宽度，mm；c为翻边宽度，mm；h为腹板高度，mm；t为壁厚，mm。

2 有限元模型

2.1 材料与单元类型

日光温室前后拱架均采用冷弯薄壁几字型钢，钢材选用Q235，杨氏模量206 GPa，泊松比0.3，钢材密度7 850 kg/m3，钢材按理想弹塑性材料考虑。为考虑几字型钢翼缘和腹板可能发生局部屈曲问题，本研究采用Shell181壳单元模拟日光温室拱架。同时，采用壳单元可精确模拟纵向系杆对日光温室拱架侧向约束位置。

2.2 荷载与边界条件

日光温室拱架自重由软件自动计算，根据《农业温室结构荷载规范》GB/T51183—2016[30]，前屋面覆盖15 mm厚发泡聚乙烯保温被，荷载取0.007 kN/m2；后屋面采用100 mm厚金属夹芯板，荷载取0.30 kN/m2；温室内固定设备荷载取0.07 kN/m2；由于暂未确定吊挂方式，作物荷载按单位面积荷载计算，取0.15 kN/m2[30]；作用于温室拱架上翼缘雪荷载水平投影值按式（1）计算。

式中k为作用于温室拱架上翼缘雪荷载，kN/m2;r为屋面积雪分布系数；t为加热影响系数，对于不加热日光温室，取值为1.0[30]；0为基本雪压，kN/m2。

考虑到风致积雪漂移现象，本研究考虑2种雪荷载分布模式：均匀分布雪荷载和非均匀分布雪荷载。2种雪荷载分布模式下的积雪分布系数如图3所示。对于均匀分布雪荷载：前屋面积雪分布系数r由前屋面水平投影（1=6.5 m）和脊高（=3.8 m）确定（r=2×1/(8×)=0.43）；后屋面积雪分布系数r,b由后屋面角（45°）确定（r,b=0.8×(60°−)/30°=0.40）。对于非均匀分布雪荷载：日光温室前屋面积雪分布系数呈三角形分布，且最大值在前屋面1/3处，覆盖保温被时，r,m最大值可取2.0[30]；后屋面积雪分布系数为0.75r,b[30]，计算得0.30。

注：L1为前屋面水平投影长度，m；H为脊高，m；α为后屋面角度，(°)；均匀分布雪荷载工况下，μr为前屋面积雪分布系数，μr,b为后屋面积雪分布系数；非均匀分布雪荷载工况下，μr,m为按照覆盖保温被工况下前屋面积雪分布系数。

根据《农业温室结构荷载规范》GB/T51183－2016[30]，日光温室按承载能力极限状态设计时，荷载基本组合的效应设计值d按式（2）计算。

式中d为荷载基本组合的效应设计值，kN/m2；G为永久荷载分项系数，取值为1.0[30]；Gk为永久荷载标准值计算的荷载效应值，kN/m2；Q1为主导可变荷载的分项系数，对于雪荷载取值为1.2[30]；Q1k为主导可变荷载标准值计算的荷载效应值，kN/m2；Qi为第个非主导可变荷载的分项系数，对于屋面活荷载、作物荷载、移动设备荷载均取1.2[30]；ci为第个非主导可变荷载的组合值系数，取值为1.0[30]；Qik为第个非主导可变荷载标准值计算的荷载效应值，kN/m2。

假定本研究日光温室拱架与基础和后墙均为固接。对于几字型钢日光温室，考虑纵向系杆对拱架侧向位移的限制作用，在有限元模型中，约束纵向系杆与拱架下翼缘连接节点处面外自由度。

2.3 模型分析方法

本研究采用一致缺陷模态法考虑日光温室拱架初始几何缺陷。在ANSYS分析过程中，首先对结构进行特征值屈曲分析，将得到的一阶屈曲模态按照一定比例叠加到理想模型中作为初始几何缺陷。在弹塑性非线性分析过程中，打开大变形开关以考虑几何非线性，为完整追踪荷载-位移曲线极限点后的平衡路径，即荷载-位移曲线下降段，采用弧长法计算日光温室拱架整个破坏过程。

3 结果与分析

3.1 失稳机理

为了分析开口截面与闭口截面日光温室拱架在雪荷载作用下失稳机理，本研究选取净截面面积、上翼缘宽度、腹板高度和壁厚均相等的几字型钢与空心矩形钢管作对比，2种截面尺寸如图4所示。经计算，2种截面净面积均为464 mm2；对于几字型钢，其绕轴的惯性矩为3.12×105mm4，绕轴的惯性矩为2.85×105mm4；对于空心矩形钢管，其绕轴的惯性矩为3.27×105mm4，绕轴的惯性矩为1.94×105mm4。

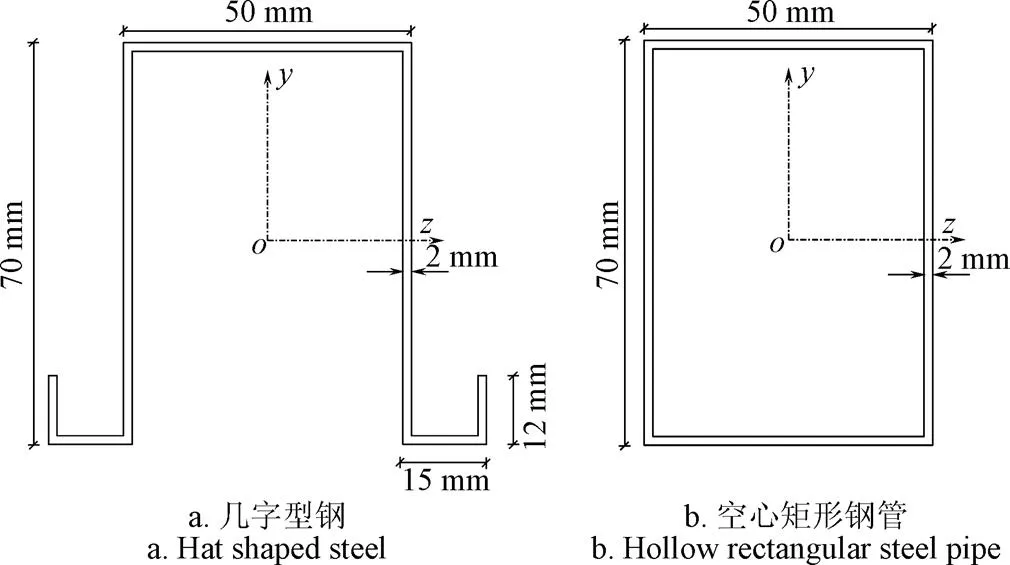
图4 截面尺寸示意图

图5展示了在雪荷载作用下，2种截面日光温室拱架屋脊节点荷载-位移曲线。由图5可知，在均匀和非均匀分布2种雪荷载工况下，拱架荷载-位移曲线变化规律相似。当荷载较小时，拱架主要发生绕轴的整体弯曲变形，由于空心矩形钢管绕轴的惯性矩稍大于几字型钢绕轴的惯性矩，因此，在相同荷载作用下，空心矩形钢管拱架位移低于几字型钢拱架。随着荷载进一步增加，拱架截面出现局部屈曲，并伴随发生绕轴的变形，由于几字型钢绕轴的惯性矩大于空心矩形钢管绕轴的惯性矩，致使几字型钢拱架极限承载力稍高于空心矩形钢管拱架极限承载力。在均匀分布雪荷载作用下，空心矩形钢管和几字型钢日光温室拱架极限承载力分别为4.13和4.29 kN/m2，2种截面日光温室拱架达到极限承载力时所发生的位移分别为26.90和39.34 mm；在非均匀分布雪荷载作用下，空心矩形钢管和几字型钢日光温室拱架极限承载力分别为1.17和1.21 kN/m2，2种截面日光温室拱架达到极限承载力时所发生的位移分别为28.17和40.70 mm；与均匀分布雪荷载作用下的极限承载力相比，此2种截面日光温室拱架在非均匀分布雪荷载作用下的极限承载力仅为均匀分布雪荷载作用下的28%。因此，此类日光温室拱架对非均匀分布雪荷载更为敏感，在温室结构设计中，应重点关注非均匀分布雪荷载情况。在接下来的分析过程中，主要讨论几字型钢日光温室拱架在非均匀分布雪荷载作用下的失稳机理。

注：A代表结构开始屈服，B代表结构达到极限承载力，C代表结构破坏。

为进一步了解几字型钢日光温室拱架在非均匀分布雪荷载作用下的破坏过程，图6展示了该温室拱架在不同雪荷载水平下的等效应力发展过程。由图6a可知，当雪荷载为0.92 kN/m2时，温室屋脊和后屋面支座处开始屈服，而其他区域均仍处于弹性状态；随着荷载的不断增加，温室屋脊和后支座处塑性区开始由翼缘向腹板扩展，同时，前屋面2/5跨度处（距离屋脊水平投影2.65 m）也开始进入屈服状态，当荷载达1.21 kN/m2时（图6b），屋脊和后屋面支座处全截面进入屈服状态，结构达到极限承载力；当达到极限承载力之后，虽然降低雪荷载可以减小屋脊处等效应力（图6c），然而，由于前屋面位移持续增加，致使前屋面2/5跨度处截面应力持续增加，当前屋面2/5跨度处全截面进入屈服状态时，结构最终发生破坏。

图6 非均匀分布雪荷载作用下等效应力

3.2 纵向系杆对极限承载力的影响

纵向系杆不仅可以传递荷载，还可以为日光温室拱架提供平面外侧向支撑，从而提高日光温室拱架平面外稳定性。本研究日光温室在前屋面和屋脊处布置4道纵向系杆（图1)。在有限元分析过程中，通过约束纵向系杆与拱架连接节点处侧向位移来考虑纵向系杆对拱架支撑作用。图7为非均匀分布雪荷载作用下，几字型钢日光温室屋脊节点处荷载-位移曲线。由图7可知，对于几字型钢日光温室拱架，纵向系杆可有效抑制拱架平面外变形，从而提高拱架极限承载力。有纵向系杆约束条件下的极限承载力约是无纵向系杆约束条件下极限承载力的1.25倍。因此，有效布置纵向系杆对提高几字型钢日光温室拱架极限承载力具有重要意义。

图7 有无系杆约束下荷载-位移曲线

3.3 初始几何缺陷对极限承载力的影响

日光温室拱架在制作、运输和组装过程中不可避免产生初始几何缺陷，由于初始几何缺陷的存在，加剧了荷载的二次效应，进而降低结构极限承载力。为了探究初始几何缺陷对拱架极限承载力的影响，本研究采用一致缺陷模态法获得拱架初始几何缺陷，即假设拱架初始几何缺陷分布与其最低阶屈曲模态一致，其初始几何缺陷如图8a所示。图8b为不同初始几何缺陷幅值下，几字型钢日光温室拱架在非均匀分布雪荷载作用下的荷载-位移曲线。由图8b可知，该日光温室拱架极限承载力随初始几何缺陷幅值的增加而降低。当初始几何缺陷幅值从5 mm增加到20 mm时，极限承载力降低了约2%，说明该日光温室拱架对初始几何缺陷敏感度较低。

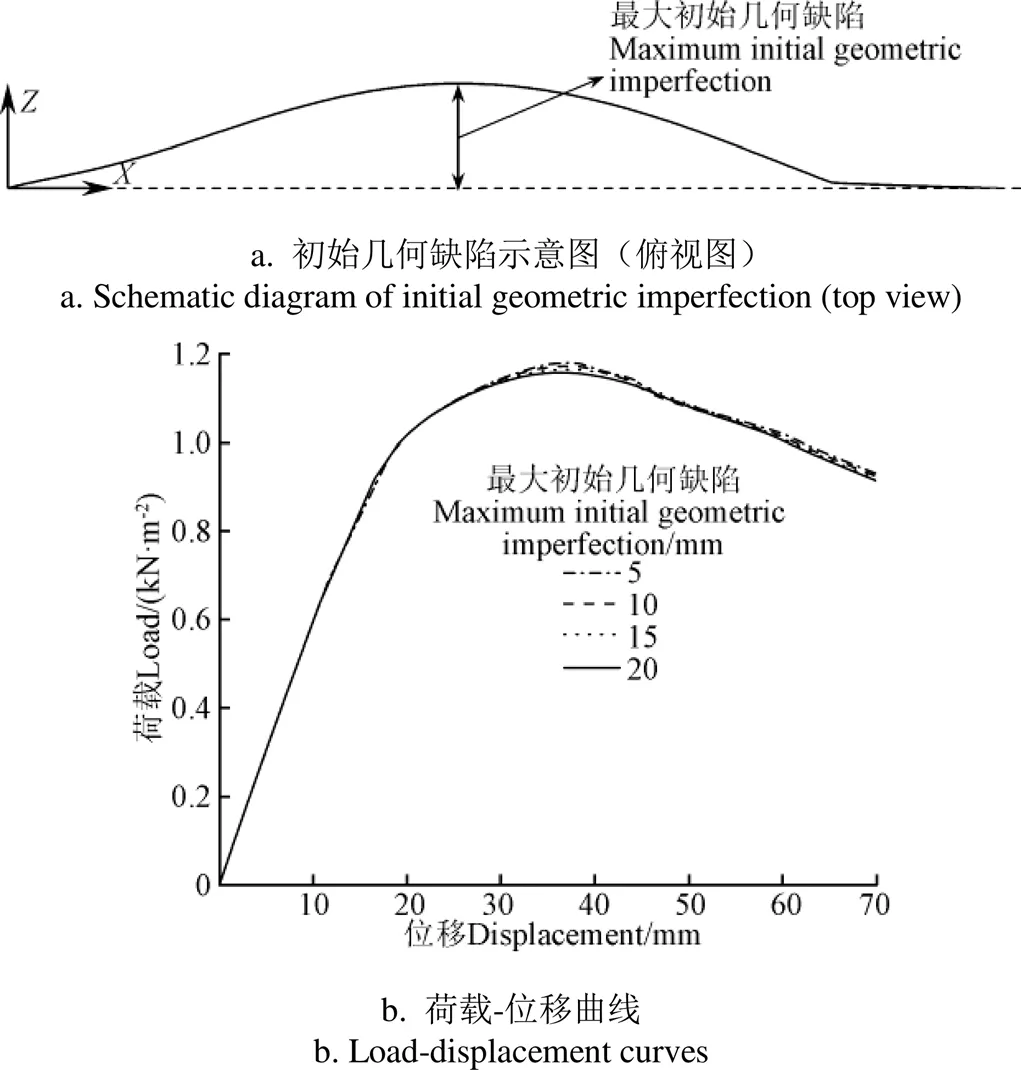
图8 初始几何缺陷对极限承载力的影响

3.4 截面参数对极限承载力的影响

当前，几字型钢截面尺寸的选取往往依据建造者经验，且缺乏相关规范参考。本节中，以截面尺寸=50 mm，=70 mm，=15 mm，=12 mm，=2 mm的几字型钢为原型，在保证净截面面积，即用钢量不变的条件下，通过改变任意2个截面参数，来探究不同截面参数对几字型钢日光温室拱架极限承载力的影响，进而为几字型钢日光温室拱架截面选取提供参考。

3.4.1 上翼缘宽度和翻边宽度

首先，在保证净截面面积、腹板高度、下翼缘宽度和壁厚不变的情况下，探究上翼缘宽度和翻边宽度对极限承载力的影响。经计算，当腹板高度=70 mm，下翼缘宽度=15 mm，壁厚=2 mm，为保证净截面面积不变，上翼缘宽度（）与翻边宽度（）需满足274 mm，当上翼缘宽度从30 mm增加到70 mm时，翻边宽度则从22 mm降到2 mm，相应上翼缘宽度与翻边宽度之比则从1.36增加到35。图9为非均匀分布雪荷载作用下，上翼缘宽度与翻边宽度之比对极限承载力的影响。由图9可知，随着上翼缘宽度与翻边宽度之比从1.36增加到35，极限承载力呈先增加后降低的变化规律。当上翼缘宽度与翻边宽度之比小于4.17时，极限承载力随上翼缘宽度与翻边宽度之比的增加而增加；当上翼缘宽度与翻边宽度之比大于4.17时，极限承载力随上翼缘宽度与翻边宽度之比的增加而降低。这是由于当上翼缘宽度增加到一定程度时，上翼缘开始出现局部屈曲，此外，随着翻边宽度的减小，翻边对下翼缘的约束作用减弱，致使极限承载力下降。当上翼缘宽度与翻边宽度之比从4.17增加到35时，极限承载力下降约13%。因此，建议几字型钢上翼缘宽度与翻边宽度之比宜控制在4.17左右。

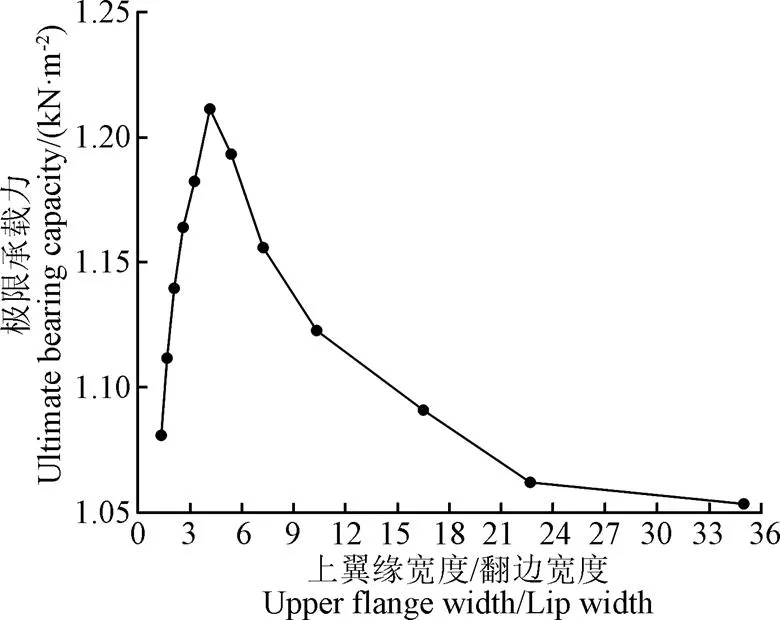
注：此分析为非均匀分布雪荷载工况。下同。

3.4.2 腹板高度和翻边宽度

在保证净截面面积、上翼缘宽度、下翼缘宽度和壁厚不变的情况下，探究腹板高度和翻边宽度对极限承载力的影响。经计算，当上翼缘宽度=50 mm，下翼缘宽度=15 mm，壁厚=2 mm，为保证净截面面积不变，腹板高度（）与翻边宽度（）需满足82 mm，当腹板高度从60 mm增加到80 mm时，翻边宽度则从22 mm降到2 mm，相应腹板高度与翻边宽度之比则从2.72增加到40。图10为非均匀分布雪荷载作用下，腹板高度与翻边宽度之比对极限承载力的影响。由图10可知，当腹板高度与翻边宽度之比小于9.25时，极限承载力随腹板高度与翻边宽度之比的增加而增加；当腹板高度与翻边宽度之比从2.72增加到9.25时，极限承载力增加约30%。而当腹板高度与翻边宽度之比大于9.25时，极限承载力几乎保持不变，这是由于当腹板增加到一定高度时，腹板开始出现屈曲，结构极限承载力由腹板局部屈曲荷载控制，因此，进一步增加腹板高度并不能提高结构极限承载力。建议几字型钢腹板高度与翻边宽度之比不大于9.25。

3.4.3 下翼缘宽度和翻边宽度

在保证净截面面积、上翼缘宽度、腹板高度和壁厚不变的情况下，探究下翼缘宽度和翻边宽度对极限承载力的影响。经计算，当上翼缘宽度=50 mm，腹板高度=70 mm，壁厚=2 mm，为保证净截面面积不变，下翼缘宽度（）与翻边宽度（）需满足27 mm，当下翼缘宽度从5 mm增加到25 mm时，翻边宽度则从22 mm降到2 mm，相应下翼缘宽度与翻边宽度之比则从0.23增加到12.5。图11为非均匀分布雪荷载作用下，下翼缘宽度与翻边宽度之比对极限承载力的影响。由图11可知，当下翼缘宽度与翻边宽度之比小于1.7时，极限承载力随下翼缘宽度与翻边宽度之比增加而增加；当下翼缘宽度与翻边宽度之比从0.23增加到1.7时，极限承载力提高约41%。因此，在不增加净截面面积、翼缘宽度和腹板高度的情况下，仅通过改变下翼缘宽度与翻边宽度之比，即可有效提升拱架极限承载力。然而，当下翼缘宽度与翻边宽度之比大于1.7时，极限承载力几乎不再随着下翼缘宽度与翻边宽度之比增加而增加，原因为：随着翻边宽度的减小，翻边对下翼缘的约束减弱，同时，随着下翼缘宽度的增加，下翼缘出现局部屈曲现象，此时拱架极限承载力由下翼缘局部屈曲荷载控制。因此，建议几字型钢下翼缘宽度与翻边宽度之比不大于1.7。

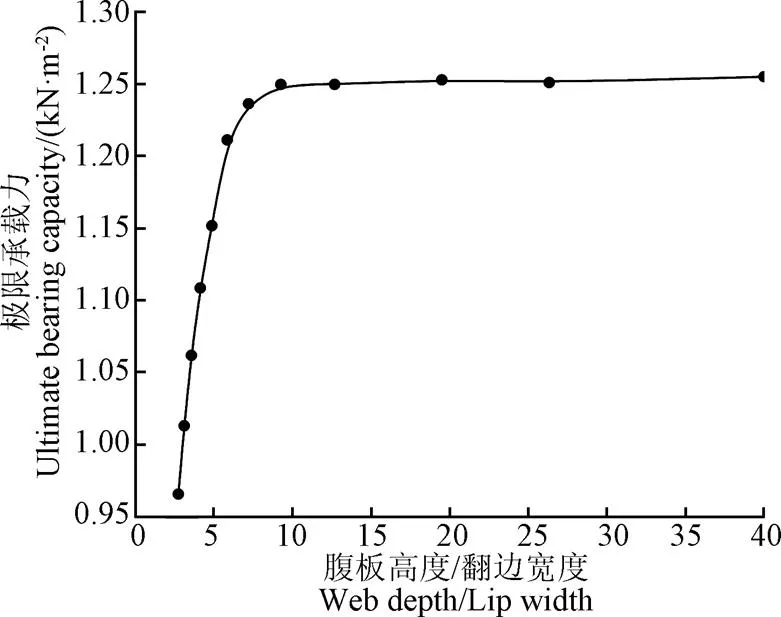
图10 腹板高度与翻边宽度之比对极限承载力的影响

图11 下翼缘宽度与翻边宽度之比对极限承载力的影响

3.4.4 上翼缘宽度和下翼缘宽度

在保证净截面面积、腹板高度、翻边宽度和壁厚不变的情况下，探究上翼缘宽度和下翼缘宽度对极限承载力的影响。经计算，当腹板高度=70 mm，翻边宽度=12 mm，壁厚=2 mm，为保证净截面面积不变，上翼缘宽度（）与下翼缘宽度（）需满足280 mm，当上翼缘宽度从30 mm增加到70 mm时，下翼缘宽度则从25 mm降到5 mm，相应上翼缘宽度与下翼缘宽度之比从1.2增加到14。图12为非均匀分布雪荷载作用下，上翼缘宽度与下翼缘宽度之比对极限承载力的影响。由图12可知，随着上翼缘宽度与下翼缘宽度之比的增加，极限承载力先上升后下降。当上翼缘宽度与下翼缘宽度之比小于3.33时，极限承载力随上翼缘宽度与下翼缘宽度之比的增加而增加；而当上翼缘宽度与下翼缘宽度之比大于3.33时，极限承载力随上翼缘宽度与下翼缘宽度之比的增加而急剧下降，这是由于随着上翼缘宽度的增加，腹板对上翼缘的约束作用减弱，同时，上翼缘宽度的增加致使其发生局部屈曲现象；此外，随着下翼缘宽度的减小，下翼缘对腹板的约束作用减弱，致使腹板也出现局部屈曲现象，从而造成极限承载力急剧下降。当上翼缘宽度与下翼缘宽度之比从3.33增加到14时，极限承载力下降约34%。因此，建议几字型钢上翼缘宽度与下翼缘宽度之比宜控制在3.33左右。

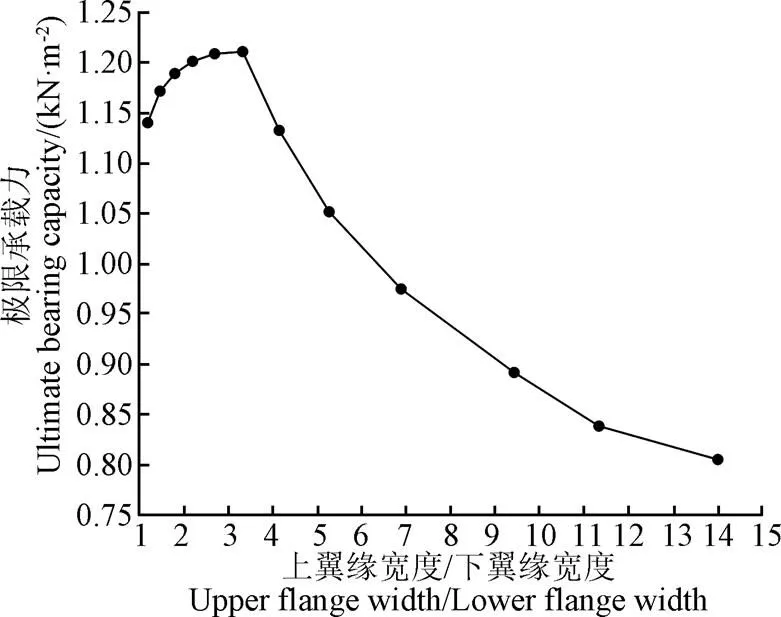
图12 上翼缘宽度与下翼缘宽度之比对极限承载力的影响

3.4.5 腹板高度和下翼缘宽度

在保证净截面面积、上翼缘宽度、翻边宽度和壁厚不变的情况下，探究腹板高度和下翼缘宽度对极限承载力的影响。经计算，当上翼缘宽度=50 mm，翻边宽度=12 mm，壁厚=2 mm，为保证净截面面积不变，腹板高度（）与下翼缘宽度（）需满足85 mm，当腹板高度从60 mm增加到80 mm时，下翼缘宽度则从25 mm降到5 mm，相应腹板高度与下翼缘宽度之比从2.4增加到16。图13为非均匀分布雪荷载作用下，腹板高度与下翼缘宽度之比对极限承载力的影响。由图13可知，随着腹板高度与下翼缘宽度之比的不断增加，极限承载力先上升后下降。当腹板高度与下翼缘宽度之比小于4.67时，极限承载力随腹板高度与下翼缘宽度之比增加而增加；然而，当腹板高度与下翼缘宽度之比大于4.67时，极限承载力随腹板高度与下翼缘宽度之比增加而下降；当腹板高度与下翼缘宽度之比从4.67增加到16时，极限承载力下降约21%，这是由于随着下翼缘宽度的减小，下翼缘对腹板的约束作用减弱，同时，由于腹板高度的增加，腹板出现局部屈曲现象，致使极限承载力降低。当腹板高度与下翼缘宽度之比为4.67时，极限承载力达到最大值。因此，建议几字型钢腹板高度与下翼缘宽度之比宜控制在4.67左右。

图13 腹板高度与下翼缘宽度之比对极限承载力的影响

4 结论与建议

本文选取某跨度为8 m，脊高为3.8 m的几字型钢日光温室为研究对象，采用ANSYS有限元软件，对其在雪荷载作用下的失稳破坏过程进行模拟，并探究了纵向系杆、初始几何缺陷和截面参数对其极限承载力的影响，得到结论如下：

1）在净截面面积、上翼缘宽度、腹板高度和壁厚相同的条件下，几字型钢日光温室拱架极限承载力稍高于空心矩形钢管日光温室拱架极限承载力。

2）相较于均匀分布雪荷载，该日光温室拱架对非均匀分布雪荷载更为敏感。几字型钢日光温室拱架在非均匀分布雪荷载作用下的极限承载力约是均匀分布雪荷载作用下的28%。因此，在日光温室结构设计中，应重点关注非均匀分布雪荷载的情况。

3）纵向系杆的设置可有效抑制几字型钢日光温室拱架平面外变形，从而提高结构极限承载力。在非均匀分布雪荷载作用下，有纵向系杆约束的极限承载力约是无纵向系杆约束条件下的1.25倍。该几字型钢日光温室拱架对初始几何缺陷敏感度较低。

4）建议几字型钢上翼缘宽度与翻边宽度之比控制在4.17左右，腹板高度与翻边宽度之比不大于9.25，下翼缘宽度与翻边宽度之比不大于1.7，上翼缘宽度与下翼缘宽度之比控制在3.33左右，腹板高度与下翼缘宽度之比控制在4.67左右。

[1] 魏晓明，周长吉，曹楠，等. 中国日光温室结构及性能的演变[J]. 江苏农业学报，2012，28(4)：855-860.

Wei Xiaoming, Zhou Changji, Cao Nan, et al. Evolution of structure and performance of Chinese solar greenhouse[J]. Jiangsu Journal of Agricultural Sciences, 2012, 28(4): 855-860. (in Chinese with English abstract)

[2] Wang C, Nan B, Wang T L, et al. Wind pressure acting on greenhouses: A review[J]. International Journal of Agricultural and Biological Engineering, 2021, 14(2): 1-8.

[3] 张琪静，刘建斌，周朝辉，等. 保护地设施果树雪灾防范与减灾技术[J]. 北方果树，2022(1)：30-33.

[4] 周长吉. 周博士考察拾零（八十二）桁架结构日光温室骨架及其构造[J]. 农业工程技术，2018，38(19)：54-61.

[5] 王斌，金宝宏，宋建夏. 竖向荷载下日光温室钢骨架承载力有限元分析[J]. 宁夏大学学报（自然科学版），2009，30(4)：336-338.

Wang Bin, Jin Baohong, Song Jianxia. Finite element analysis of load bearing capacity of steel skeletons for solar greenhouses under vertical loads[J]. Journal of Ningxia University (Natural Science Edition), 2009, 30(4): 336-338. (in Chinese with English abstract)

[6] 唐中祺，刘丽霞，王瑞东，等. 两种日光温室钢骨架结构安全性能分析[J]. 甘肃农业大学学报，2016，51(6)：53-57.

Tang Zhongqi, Liu Lixia, Wang Ruidong, et al. Safety performance of two steel frames of solar greenhouse[J]. Journal of Gansu Agricultural University, 2016, 51(6): 53-57. (in Chinese with English abstract)

[7] 王洪义，祖歌，杨凤军，等. 高纬度地区多功能日光温室设计[J]. 农业工程学报，2020，36(6)：170-178.

Wang Hongyi, Zu Ge, Yang Fengjun, et al. Design of multi-functional solar greenhouses in high latitude areas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(6): 170-178. (in Chinese with English abstract)

[8] 关瑞，吴坚勇，刘中华，等. 日光温室钢架结构分析及优化[J]. 山西农业大学学报（自然科学版），2019，39(6)：100-106.

Guan Rui, Wu Jianyong, Liu Zhonghua, et al. Analysis and optimization of greenhouse steel frame structure[J]. Journal of Shanxi Agricultural University (Natural Science Edition), 2019, 39(6): 100-106. (in Chinese with English abstract)

[9] 郄丽娟，赵献辉，许广义，等. 三连栋日光温室拱式桁架结构静力分析与结构优化[J]. 中国农学通报，2014，30(35)：242-247.

Qie Lijuan, Zhao Xianhui, Xu Guangyi, et al. Static analysis of truss type steel structure for three-span sunlight greenhouse[J]. Chinese Agricultural Science Bulletin, 2014, 30(35): 242-247. (in Chinese with English abstract)

[10] 袁余，赵惊鹏，张程，等. 日光温室结构拓扑优化设计[J]. 农机化研究，2013，35(10)：55-59.

Yuan Yu, Zhao Jingpeng, Zhang Cheng, et al. The topological optimization design of the structure of the solar greehouse[J]. Journal of Agricultural Mechanization Research, 2013, 35(10): 55-59. (in Chinese with English abstract)

[11] 周凤，何斌. 日光温室新型装配式骨架节点设计与有限元分析[J]. 北方园艺，2021(12)：50-56.

Zhou Feng, He Bin. Design and finite element analysis of new fabricated skeleton joints in solar greenhouse[J]. Northern Horticulture, 2021(12): 50-56. (in Chinese with English abstract)

[12] 姜迎春，白义奎，王永刚，等. 考虑脉动风速的平面刚架日光温室结构动力响应规律[J]. 中国农业大学学报，2019，24(4)：136-147.

Jiang Yingchun, Bai Yikui, Wang Yonggang, et al. Dynamic response analyses of plane frame solar greenhouse considering fluctuating wind speed[J]. Journal of China Agricultural University, 2019, 24(4): 136-147. (in Chinese with English abstract)

[13] Wang C, Jiang Y C, Li X Y, et al. Wind-induced vibration response analysis of Chinese solar greenhouses[J]. Computers and Electronics in Agriculture, 2021, 181: 105954.

[14] 周长吉. 中国日光温室结构的改良与创新(四)：温室骨架形式的改良与创新[J]. 中国蔬菜，2020(7)：1-6.

[15] 周长吉. 周博士考察拾零（一百零一）单管骨架日光温室结构及其构造[J]. 农业工程技术，2020，40(4)：49-54.

[16] 齐飞，闫冬梅，胡林，等. 日光温室荷载组合方法及应用[J]. 农业工程学报，2022，38(7)：264-271.

Qi Fei, Yan Dongmei, Hu Lin, et al. Method and application of load combination in solar greenhouses[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 264-271. (in Chinese with English abstract)

[17] 丁敏，施旭栋，李密密，等. 薄膜承载力及其对日光温室结构稳定性能的影响[J]. 农业工程学报，2013，29(12)：194-202.

Ding Min, Shi Xudong, Li Mimi, et al. Load-bearing capacity of films and its effect on structure stability of Chinese solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(12): 194-202. (in Chinese with English abstract)

[18] 丁敏，李密密，施旭栋，等. 考虑覆盖材料蒙皮效应的温室结构稳定承载力计算[J]. 农业工程学报，2016，32(增刊1)：224-232.

Ding Min, Li Mimi, Shi Xudong, et al. Stable bearing capacity calculation of greenhouse structures considering skin effect of covering material[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(Supp.1): 224-232. (in Chinese with English abstract)

[19] 闫冬梅，胡林，周长吉，等. 椭圆管单管拱架日光温室结构性能分析[J]. 农业工程学报，2022，38(5)：217-224.

Yan Dongmei, Hu Lin, Zhou Changji, et al. Analysis of the performance of the oval tube arch of single-tube solar greenhouses[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(5): 217-224. (in Chinese with English abstract)

[20] 齐飞，闫冬梅，魏晓明. 日光温室前屋面支撑位置对实腹式骨架安全性的影响[J]. 农业工程学报，2020，36(16)：174-181.

Qi Fei, Yan Dongmei, Wei Xiaoming. Influences of south roof support position change on the skeleton structure safety in solid belly solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(16): 174-181. (in Chinese with English abstract)

[21] 杨升华，刘雪迎，蒋秀根. 基于临时加固策略的日光温室极端风雪灾害对策[J]. 江苏大学学报（自然科学版），2022，43(1)：45-53.

Yang Shenghua, Liu Xueying, Jiang Xiugen. Countermeasures against extreme wind and snow disasters to solar greenhouses based on temporary reinforcement[J]. Journal of Jiangsu University (Natural Science Edition), 2022, 43(1): 45-53. (in Chinese with English abstract)

[22] Wang C, Jiang Y C, Bai Y K, et al. Numerical study on static properties and failure mechanisms of landing assembled Chinese solar greenhouses[J]. Computers and Electronics in Agriculture, 2021, 188: 106347.

[23] Wang C, Jiang Y C, Wang T L, et al. Analysis of wind-induced responses of landing assembled Chinese solar greenhouses[J]. Biosystems Engineering, 2022, 220: 214-232.

[24] Li X Y, Wang C, Jiang Y C, et al. Dynamic response analysis of a whole steel frame solar greenhouse under wind loads[J]. Scientific Reports, 2022, 12(1): 5200

[25] 白义奎，王鸿，王铁良，等. 新型钢骨架结构日光温室设计与测试[J]. 沈阳农业大学学报，2013，44(5)：542-547.

Bai Yikui, Wang Hong, Wang Tieliang, et al. Design and test of new steel frame solar greenhouse[J]. Journal of Shenyang Agricultural University, 2013, 44(5): 542-547. (in Chinese with English abstract)

[26] 张京社，柴文臣. 高寒区现代日光温室结构设计与建造[J]. 山西农业科学，2012，40(8)：870-873.

Zhang Jingshe, Chai Wenchen. Modern solar greenhouse structure design and construction in high latitude and cold climate areas[J]. Journal of Shanxi Agricultural Sciences, 2012, 40(8): 870-873. (in Chinese with English abstract)

[27] 周长吉. 周博士考察拾零（九十八）以EPS空腔模块为围护墙体的钢骨架装配式日光温室[J]. 农业工程技术，2019，39(31)：26-34.

[28] 周长吉. 周博士考察拾零（一百二十七）一种自防水无拼缝橡塑保温被围护的主动储放热组装结构日光温室——记北京华美沃龙农业科技有限公司的创新[J]. 农业工程技术，2022，42(10)：36-45.

[29] 赵云，丁敏，韩盛柏，等. 考虑压-弯-扭耦合作用的开口截面杆件非线性静力模型[J]. 中国农业大学学报，2021，26(3)：115-123.

Zhao Yun, Ding Min, Han Shengbai, et al. Nonlinear static model for the bar with open-section considering pressure-bending-torsion coupling[J]. Journal of China Agricultural University, 2021, 26(3): 115-123. (in Chinese with English abstract)

[30] 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局. 农业温室结构荷载规范：GB/T 51183-2016[S]. 北京：中国计划出版社，2016.

Ultimate bearing capacity of the solar greenhouse with hat-shaped steel under snow loads

Wang Cong1, Jiang Yingchun2, Xu Zhanyang1, Zhang Feng1, Bai Yikui1, Wang Tieliang1※

(1.110866; 2.110866)

Hat-shaped steel members are widely used in solar greenhouses, due to their low cost, fast construction, and high material efficiency. This study aims to determine the ultimate bearing capacity of a solar greenhouse with the hat-shaped steel under snow loads. The typical solar greenhouse with an 8 m span and 3.8 m ridge height was selected as the research object. The finite element method (FEM) under ANSYS software was used to analyze the instability mechanism and failure modal of the structure under snow loads (uniform and non-uniform snow loads). An investigation was made to clarify the effects of the longitudinal tie bars, initial geometric imperfections, and sectional dimensions on the ultimate bearing capacity of the structure under non-uniform snow loads. Both the material and geometrical nonlinearity were considered in the finite element model. A bilinear kinematic hardening model was adopted for the steel with a yield strength of 235 MPa, Young’s modulus of 206 GPa, and Poisson’s ratio of 0.3. The geometrical nonlinearity was activated using the ‘NLGEOM’ option. To consider the local buckling, the greenhouse skeletons were then modeled with the Shell181 element suitable for the large strains and rotations. Fixed hinge supports were used for both ends of the skeleton. An arc-length method was utilized to trace the nonlinear load-displacement curve, in order to calculate the ultimate bearing capacity of the structure under snow loads. The ultimate bearing capacity of the solar greenhouse with the hat-shaped steel was slightly higher than that of the hollow rectangular section under the same conditions of net section area, upper flange width, web depth, and wall thickness. The solar greenhouse was more sensitive to the non-uniform snow loads, compared with the uniform ones. The ultimate bearing capacity of the hat-shaped steel solar greenhouse under non-uniform snow loads was about 28% of that under uniform snow loads. Therefore, some suggestions were presented for the non-uniform snow loads in the design stage of the solar greenhouse structure. The roof ridge and north roof end were dangerous sections under non-uniform snow loads, which firstly entered the full section yield state. The longitudinal tie bars were expected to effectively improve the ultimate bearing capacity of the greenhouse structure. The ultimate bearing capacity of the structure with the longitudinal tie bars was about 1.25 times that without tie bars. The ultimate bearing capacity was only reduced by 2%, when the initial geometric imperfections amplitude increased from 5 to 20 mm. It infers that the solar greenhouse was not sensitive to the initial geometric imperfection. The cross-section size of a hat-shaped steel was recommended that the ratio of the upper flange width to the lip width, the upper flange width to the lower flange width, and the web depth to the lower flange width were about 4.17, 3.33, and 4.67, respectively, while, the ratio of the web depth to the lip width, and the lower flange width to lip width were less than 9.25 and 1.7, respectively. These findings can provide a strong reference for the solar greenhouse with the open cold-formed thin-walled steel under snow loads.

greenhouse; bearing capacity; load; finite element method; buckling failure; cold-formed thin-walled steel; open section; sectional optimization

10.11975/j.issn.1002-6819.2022.19.019

S26; S625.1; TU261

A

1002-6819(2022)-19-0172-08

王聪，姜迎春，徐占洋，等. 雪荷载作用下几字型钢日光温室极限承载力分析[J]. 农业工程学报，2022，38(19)：172-179.doi：10.11975/j.issn.1002-6819.2022.19.019 http://www.tcsae.org

Wang Cong, Jiang Yingchun, Xu Zhanyang, et al. Ultimate bearing capacity of the solar greenhouse with hat-shaped steel under snow loads[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(19): 172-179. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.19.019 http://www.tcsae.org

2022-08-30

2022-09-30

辽宁省重点研发项目（2021JH2/10200022）；辽宁省科学研究经费项目（LJKZ0689）；国家建设高水平大学公派研究生项目（202108210256）；沈阳农业大学研究生创新培育项目（2022YCXB02）

王聪，博士生，研究方向为农业设施与环境工程。Email：congwang@stu.syau.edu.cn

王铁良，教授，博士生导师，研究方向为农业设施与环境工程。Email：tieliangwang@syau.edu.cn