基于强化学习的脓毒症用药策略研究

王德勇，张天逸，程云章

(上海理工大学 上海介入医疗器械工程技术研究中心，上海 200093)

引言

脓毒症及脓毒性休克是临床常见的危重症，是导致全球重症患者死亡的主要原因之一[1]。当患者感染严重时,除抗生素和感染源控制外，还需配合升压药和静脉输液的治疗。不同的升压药和静脉输液治疗策略会导致患者生存率的变化[2]，因此,二者的给药策略一直是脓毒症药物治疗研究的热点问题[3]。近几年，国际上努力为脓毒症治疗提供一般性指导，但临床医生仍然缺乏有效工具来提供实时有效的个性化决策支持[4]。同时有研究表明，新定义的出现以及临床数据的积累都会对临床决策产生重要影响[5]，因此，如何利用现有数据为临床提供一般性指导具有重要研究价值。Liang等[6]首先利用带有优先级回放的Dueling DQN(Deep Q-network)和Double DQN网络构建了一种名为D3QN的网络，该模型可以主动学习样本之间的关系，最后利用MIMIC-III数据集对模型进行验证，结果表明，模型性能相对于baseline有显著提升。其中，基于权重的双重鲁棒性离策略评估值比最佳的baseline值高7.4%，比临床医生的策略值高26.3%，但由于数据集有限以及模型模仿的是临床医生的经验治疗原则，仍无法获取最佳治疗方案。针对传统强化学习方法只考虑了患者的最终状态，未考虑患者中间状态和短时间内用药量的变化情况，Lu[7]基于现有模型开发了一种利用SOFA评分和动脉乳酸水平评估患者中间状态的模型，通过增大血管升压药惩罚来解决用药量的急剧变化，结果表明，该模型不仅策略评估值优于临床策略评估值,同时预估的死亡率也低于临床数据。Roggeveen等[8]首先利用T分布随机近邻嵌入和序贯器官衰竭评分(sequential organ failure assessment, SOFA)来探索患者之间群体的差异，之后又引入一种新的深度策略来分析模型所得策略的可解释性，以评估模型的安全性和可靠性。Yuan等[9]选取与脓毒症相关的106个特征构建带有标签的数据集，利用极度梯度提升(extreme gradient boosting, XGBoost)模型将脓毒症的预测准确率提高到了82%。Jia等[10]在机器学习模型的基础上提出一种“安全驱动设计”的方法，结果表明，该方法可以有效识别机器学习模型的不安全行为，特别是血管升压药用量的急剧变化，有效地提高了模型的安全性。Peng等[11]利用核函数学习和深度强化学习来获取脓毒症的治疗策略，结果表明，混合学习方式相对于独立DQN学习和核函数学习方法表现更好。

目前，国内对于脓毒症的研究大部分还处于基础阶段，利用人工智能技术辅助脓毒症治疗的相关研究较少。齐霜等[12]基于MIMIC-III数据集构建出XGBoost预测模型，测试结果表明，该模型较临床常用评分指标能更准确地预测脓毒症患者的死亡风险，有助于辅助临床决策，分配医疗资源。任国奇[13]使用基于深度逆强化学习最小树模型和基于对偶权重的异策略评估方法去学习和评估脓毒症治疗策略，结果表明，新模型得到的治疗策略可以将临床患者的总体死亡率降低3.3%。蒋容[14]利用大数据技术对临床数据进行分析，首先分析哪些因素对患者的预后影响较大，然后在此基础上建立脓毒症预警模型，结果表明，该预警模型在一定程度上可以帮助医生提早判断患者状态。潘盼等[15]利用强化学习方法研究脓毒症治疗过程中液体平衡对于患者死亡率的影响，结果表明，该模型可以准确地预测液体治疗的方向。

脓毒症诊断一般使用脓毒症拯救运动指南发布的Sepsis标准，本研究依据Sepsis3.0标准从MIMIC数据集中识别脓毒症患者。 2016年专家组提出Sepsis3.0诊断标准，此标准抛弃了容易造成过估计的SIRS指数，采用新设计的SOFA评分指标，具体评分细则见表1[16-17]。

表1 SOFA评分表

1 数据来源

本研究采用的数据集是MIMIC(medical information mart for intensive care，MIMIC)数据库。该数据库由美国麻省理工学院计算生理学实验室、贝斯以色列迪康医学中心以及飞利浦医疗共同发布，数据库中收集整理了2001-2012年期间住在贝斯以色列迪康医学中心重症监护室数万名真实患者的临床诊疗信息[18], 该数据库不仅可以用于研究脓毒症相关的问题，在其它领域也有广泛应用[19-20]。本研究选择采用MIMICⅢv1.4版本的患者数据，共含有46 520位患者。

2 动态规划原理

为评估一个治疗策略π的期望回报，一般会涉及两个值函数：状态值函数和状态-动作值函数，本研究中状态指某一时刻患者的临床状态，即各项指标值，动作指患者的静脉输液量和血管加压药的用量。这两类值函数是本研究建模解法的基础。

在患者状态存在终止的情况下，总回报的计算如下 ：

(1)

本研究患者的最终状态为存活或死亡，因此对应该情况，若环境无终止状态，即T=∞，称为持续性强化学习任务，其回报也可能是无穷大，为解决该问题，可以引入一个折扣率来降低远期回报的比重，在无终止状态时，总回报的计算见式(2)：

(2)

其中，γ代表折扣率，其取值在0～1之间，本研究中γ取值为0.9。

2.1 状态值函数

状态值函数定义为脓毒症患者在某个状态s下，执行一个用药策略π到最终状态可以获得的回报，使用公式Vπ(s)来表示，一个用药策略π的总期望回报，计算如下：

(3)

其中，状态值函数Vπ(s)见式(4)：

(4)

式(4)的含义是：患者从某一状态s出发所能得到的总回报等于以状态s为初始状态，在策略π下所有可能用药策略回报的期望。根据马尔科夫性，Vπ(s)展开可以得到：

Vπ(s)=Ea～π(a|s)Es′～p(s′|s,a)[r(s,a,s′)+γVπ(s′)]

(5)

式(5)称为贝尔曼方程，表示患者当前状态的值函数可以通过下一个状态的值函数计算。

2.2 状态动作值函数

状态动作值函数指患者以s为初始状态并执行用药策略a，然后在策略π下得到的总期望回报，也称其为Q函数。

Qπ(s,a)=Es′～p(s′|s,a)[r(s,a,s′)+γVπ(s′)]

(6)

式(6)表示在状态s下，执行用药量a得到的期望回报，Qπ(s,a)为执行用药量a后的下一个可能状态s′的值函数Vπ(s′)的折扣期望加上本次获得的奖励r(s,a,s′)。同时，由于状态值函数Vπ(s)是Q函数Qπ(s,a)关于用药量a的期望，则有：

Vπ(s)=Ea～π(a|s)[Qπ(s,a)]

(7)

由式(6)、式(7)可以将Q函数写成如下关于Q函数的贝尔曼方程：

Qπ(s,a)=Es′～p(s′|s,a)[r(s,a,s′)+γEa′～π(a′|s′)[Qπ(s′,a′)]]

(8)

2.3 策略迭代

策略迭代指从一个初始用药策略出发，先进行策略评估，即评价患者在该用药策略下可以获得的状态价值，然后改进策略，进行策略提升，得到新的用药策略，之后再对改进的策略进行策略评估，如此经过不断地更新迭代，最后求出一个最佳的用药策略。

2.3.1策略评估 策略评估指计算用药策略的状态值函数Vπ(s)，即计算在当前用药策略π下每一个状态的价值，计算方式如下：

(9)

2.3.2策略提升 计算策略价值函数是为找到更好的用药策略。在策略评估基础上，得到在上一策略下每一个状态的价值，基于该状态价值可对策略进行改进，得到更好的策略。

计算在每一个状态采取相应用药量后到达下一状态获得的期望价值，即状态动作值函数，计算期望的公式见式(10)。

(10)

在得到每一个状态采取不同用药量获取的价值后，选取价值最高的状态动作对，即选取某个状态下应采取多少用药量，将其设置新的用药策略π，在计算完所有的状态动作值函数后即可得到新的策略π。

(11)

将式(10)代入式(11)即可得到简化后的计算公式，见式(12)：

(12)

2.4 价值迭代

策略迭代的策略评估需要值函数完全收敛方可进行策略提升，若对策略评估要求放低，速度会有所提升。同时，策略迭代中关注的是最优策略，若此时有方法可以使最优值函数和最优策略同时收敛，即可只关注值函数的收敛过程，只要值函数达到最优，那么策略也就是最优的。针对以上思路提出的价值迭代相较于策略迭代过程简单。对于患者所有当前状态，计算每一个可能的用药量到达下一个状态获得的期望价值，选取期望价值函数最大的用药量，然后将该最大期望价值函数设为当前状态的价值函数，之后继续迭代，直至收敛。计算方式见式(13)：

(13)

3 数据处理

3.1 MIMIC数据预处理

MIMICⅢ数据库共有46张数据表，数据量庞大，为了便于实验研究，降低实验复杂度，首先要提取与脓毒症治疗以及和本研究相关的临床数据，例如患者的人口统计学信息，用药情况，实验室检查指标等，本研究提取的脓毒症患者部分数据指标借鉴了文献[9]。数据的主要处理流程见图1。

图1 数据预处理流程

本研究采用Sepsis3.0标准，因此在计算SOFA指数前，需要先判断发生感染的患者。本研究遵守了诊断脓毒症的原始时间标准，首次使用抗生素时，在24 h之内收集微生物样本，在首次收集微生物样本时，必须在72 h之内使用抗生素。为尽可能多获取患者数据，同时兼顾模型的复杂度，本研究最长只获取患者80 h的临床数据，并在此数据基础上，对数据进行清洗。数据清洗时，首先，排除年龄小于18岁的患者，保留研究对象为成年患者。其次，排除死亡率无记录或中途退出治疗的患者，因为本实验采用判断患者存活与否作为奖励的标准，若死亡率未定义，此患者的轨迹奖励将不完整，会对模型的建立和结果产生负面影响。本研究对象是血管升压药和静脉输液用量，静脉输液量和血管升压药用量未记录的数据对实验结果有较大影响，因此，这些数据也被排除。对于其它实验需要用到的非核心数据指标，例如血压、心率等数据，本研究采用K-近邻(K-nearest neighbor, KNN)插值法，对缺失值进行补全。同时数据在记录过程中难免会有偏差导致离群值出现，本研究根据不同指标的临床实际意义进行对应处理。除MIMICⅢ数据库里可直接获得的指标，本研究中还采用一些衍生指标，即通过现有数据计算得到的指标，例如氧合指数(P/F), 休克指数(Shock Index), SOFA, SIRS等。本研究最终提取了48个指标进行模型训练，详细指标见表2。

表2 研究指标

表2(续)

不同患者数据记录时间差可能有较大差异，为保持患者数据序列统一性，需要对数据进行编码，本研究采用4 h时间步长对数据进行编码，编码后的数据为脓毒症患者的治疗轨迹。本研究在4 h时间步长内，根据不同指标的临床实际意义和模型训练需要，部分数据指标在计算时取平均值(例如心率，血压以及动脉乳酸值等参数)，部分取4 h时间步长内的总和(例如静脉输液量和尿量等参数)。

3.2 行为定义

本研究对象是血管升压药以及静脉输液用量，但在MIMIC数据集中血管升压药以及静脉输液都包括多种药品，因此，在处理时需要进行统一化处理。对于血管升压药，实验中都转化为去甲肾上腺素当量进行处理，单位是ug/kg/min，当体重缺失时使用80 kg代替处理。其中1 ug肾上腺素等于1 ug去甲肾上腺素，100 ug多巴胺等于1 ug去甲肾上腺素，2.2 ug去氧肾上腺素等于1 ug去甲肾上腺素，1个单位加压素等于5 ug去甲肾上腺素。静脉输液在本研究中选取胰岛素给药、晶体输液、胶体类输液以及血液制品，这些不同种类的液体最后根据张力对输入速率进行标准化[21-22]。本研究仅预测在指定时间段内患者血管升压药以及静脉输液的总用量，并不涉及给药速度的预测。

3.3 模型定义

图2是本研究中动态规划解法的详细步骤。动态规划是基于模型的求解方式，需要知道完整的动作空间，状态空间，状态转移概率，以及每一步的奖励等信息。本研究对象是静脉输液量和血管升压药的用量，为构建状态空间，采用零和四分位数表示方法，将每种药的用药量离散到五个状态空间里，两种药就构成离散的25个动作空间。本研究采用K均值聚类(K-means)方式得到模型状态空间，此聚类方式中K值的定义对结果影响较大。本研究在实验测试和文献调研基础上，将最终状态空间数定义为750。基于构建的状态空间和动作空间，然后利用预处理部分得到的患者轨迹计算患者在每个状态的状态转移概率。本研究设定每一步动作之后的奖励见表3。其中吸收态指每位患者治疗轨迹的最后一步(在MIMIC数据集里对应患者出院后的48 h之内是否存活)，其它状态都属于中间状态。

表3 状态价值对应关系

4 实验结果

4.1 验证方法

(14)

图2 模型训练迭代步骤Fig.2 Model trains iterative steps

4.2 实验结果分析

本研究测试集在不同策略下的平均回报见表4。

表4 不同策略平均回报

由实验结果可知，不管是策略迭代还是价值迭代得到的策略结果都优于临床用药策略，同时由于策略迭代和价值迭代底层原理类似，因此，当二者都收敛时，期望回报几乎相同。

在本研究价值迭代计算中，当患者前后状态价值差值θ小于1e-20时，判断其达到收敛。策略迭代中策略评估用其作为收敛的标准，但整个策略迭代的结束标准是前后两次迭代得到的策略相同。对于价值迭代解法，当所有状态的前后两次状态价值误差总和小于θ时，判断其达到收敛。图3是整个价值迭代收敛的过程，可见，在前几次迭代中误差急剧降低，但在后面的迭代中每次误差的降低微乎其微，若在θ值不是很小的情况下，价值迭代的次数会大幅度减少。

图3 价值迭代收敛图

图4是策略迭代的收敛过程图，六个尖峰表示策略迭代总共经历六次，每两个尖峰之间是策略评估的收敛过程。由图可见，策略评估的收敛轨迹和价值迭代类似，这是因为策略评估本质上就是价值迭代的过程。

策略迭代和价值迭代收敛速度见表5。虽然策略迭代和价值迭代所得策略的期望回报几乎相同，但二者的收敛速度相差较大。价值迭代方法中策略评估只需一次迭代，计算量少，但总迭代次数较多导致收敛较慢，而策略迭代每一次迭代计算量大，但迭代次数较少，收敛较快。由图3、图4可知，虽然策略迭代在总的迭代次数上远小于价值迭代的总迭代次数，但策略迭代在每次策略评估和策略提升中迭代次数都较大，这也是策略迭代计算量大的原因。在实际应用中，当数据量有限时，推荐使用策略迭代去改进临床实际用药策略。

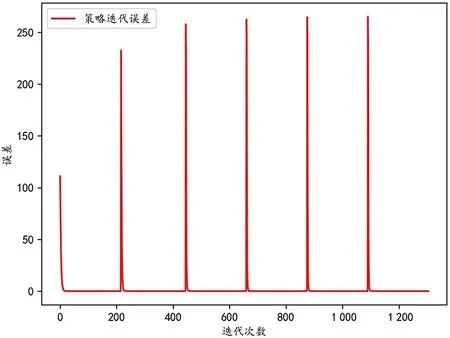
图4 策略迭代收敛图

表5 不同方法迭代次数

5 结语

本研究基于MIMICⅢ 数据集，根据Sepsis3.0的定义，识别发生感染的患者，数据清洗完，将数据编码成4 h时间步长的序列，并在每个序列里计算对应的SOFA值，最后利用价值迭代和策略迭代对序列数据进行训练，得到两套脓毒症中血管升压药和静脉输液量的用药策略。在实验验证阶段，本研究在不同患者治疗轨迹上，分别计算训练得到的两套用药策略和临床医生实际用药策略的平均回报，结果表明，利用动态规划解法得到的用药策略具有一定参考价值，同时在策略迭代和价值迭代都收敛时，二者结果几乎一样，但策略迭代在收敛速度上要远高于价值迭代。

本研究采用的建模方法是价值迭代和策略迭代，二者都属于动态规划解法。该类方法需要预先知道所有的状态空间、动作空间以及状态转移概率，但在现实环境中这些信息很难获取，因此，该类方法并不具备通用性。同时，随着训练数据量的增大，不管是价值迭代还是策略迭代，要使其收敛，必将伴随着巨大的迭代次数，效率很低。因此，后续可考虑采用时序差分学习的方式学习用药策略。时序差分学习结合了动态规划和蒙特卡洛解法，一方面它和蒙特卡洛解法一样，无需具体的环境信息，另一方面又继承了动态规划算法的自举特性，可以利用之前学习到的价值去更新值函数，不必等到一个episode结束后才去更新值函数，可显著提高更新的效率。此外，本研究仅提取了48个患者生命体征参数，后续还需要继续调研文献，并通过实验验证参数中是否存在冗余。