基于BPE与自更新马尔科夫链的耳鸣康复音乐合成方法*

方一鸣，何培宇，方安成，邓茗月，潘帆

(四川大学电子信息学院,成都 610065)

引言

耳鸣是在没有外界声音刺激时的一种主观听觉感知[1]，可导致患者睡眠障碍、焦虑、注意力不集中，严重影响患者的生活质量。由于目前耳鸣发病机制尚不确定[2]，因此,还没有治疗耳鸣的明确手段。音乐疗法是一种无创伤性的治疗方法，由于其无副作用且方法柔和，而广泛应用于耳鸣的临床治疗[3]。

目前，国外针对耳鸣的音乐疗法主要包括Neuromonics耳鸣疗法(neuromonics tinnitus treatment, NTT)[4]、切迹滤波音乐(tailor-made notched music,TMNM)疗法[5]、海德堡神经音乐疗法[6]。但上述几种方法适用范围有限、方案复杂，且使用的音乐都需重复播放[4,6-7]，易唤起患者的不良记忆及潜在负面情绪，达不到预期的减压效果[8]。根据人工创作的音乐具有自相似特性[9]，程冉等[10]使用LS文法、陈杰梅等[11]基于五声音阶和混沌、徐媛媛等[12]基于IFS分形算法和分解和弦、金宁敏等[13]基于超混沌算法、蔡丽等[14]基于迭代系统、漆蕾宇等[15]使用IFS分形算法从音乐的曲调、节奏以及和声三方面来生成理论上无限长，具有自相似特点，又不完全重复的耳鸣康复音乐。然而以上方法生成的音乐可听性不足，并且存在着音高突变的缺陷。随着技术的发展，Chen等[16]基于已有音乐片段和长短期记忆(LSTM)生成相似不完全重复，且能更好满足耳鸣患者偏好的音乐，并临床验证了合成相似不重复音乐对治疗耳鸣具有一定的效果。但是，该方法仍然存在着合成音乐不自然、拼接痕迹明显、每首原始音乐都需要专门设计和训练一组LSTM模型等问题，因而不便于临床上的推广应用。

针对上述问题，本研究提出一种以患者偏好的音乐为基础，无需训练且适用于所有原始音乐的耳鸣治疗音乐合成方法。该方法使用字节对编码对原始音乐主旋律声部的信息进行编码，将音乐表示成词向量的组合形式，即音乐块的组合形式。同时，本研究对马尔科夫链状态转换过程可能会失去下一个转移状态的问题进行了改进，提出可以连续进行状态转换的自更新马尔科夫链。将字节对编码后的音乐块作为自更新马尔科夫链的状态，利用自更新马尔科夫链的状态转移来生成任意时长音乐。

仿真及试听结果表明，本研究方法不仅理论上可以生成无限长、相似且不完全重复的满足耳鸣治疗的音乐，且生成模型简单并具有普适性，生成的音乐听感自然、无拼接痕迹、和原曲相似度高，可满足音乐偏好的需求。

1 字节对编码和自更新马尔科夫链原理

1.1 字节对编码

在音乐的生成过程中需要将音乐切分成块，但是预先制定的切分方法并非适用于每首音乐，因此，本研究采用字节对编码(byte pair encoding，BPE)自动学习音符及和弦间的最佳组合方式，使得切分后的音乐块中的音符、和弦之间存在更强的依存关系。

BPE算法最早用于数据压缩,原理是找到常见的可以组成单词的子字符串，又称子词，然后将每个词用这些子词来表示。BPE中最基本的子词就是所有字符的集合，如{a,b,…,z,A,B,…,Z}。之后，通过不断统计文本中所有相邻子词的出现次数，选出出现频率最高的一对子词，并将这一对子词组合起来视为一个新的子词，使用文本中未出现过的符号代替这一对子词，直到满足某个停止条件，如:统计词对的频率最高不超过某个频率阈值，其算法流程见图1。

图1 BPE算法流程Fig.1 BPE algorithm flow chart

1.2 自更新马尔科夫链

1.2.1马尔科夫链 马尔科夫链可以根据当前状态预测未来状态，在多种状态之间进行状态转移，本研究利用该特性实现理论上无限长音乐的生成。

马尔科夫链是一组具有马尔科夫性质的离散随机变量集合，马尔科夫性质指将来的状态仅与当前时刻的状态有关，而与过去时刻的状态无关。即对于一个随机过程{Xn,n∈T}，若随机变量的取值都在可数集I内，对于任意的非负整数n∈T，条件概率满足式(1)：

p(Xn+1|Xn,…,X1)=P(Xn+1|Xn)

(1)

则{Xn,n∈T}被称为马尔科夫链，可数集I∈Z被称为状态空间，马尔科夫链在状态空间内的取值称为状态。

当状态也离散取值，系统在时刻n处于状态i，在时刻n+1处于状态j的概率可表示为：

τij=P[Xn+1=j|Xn=i]

(2)

此情况下，条件概率τij称为转移概率，其中，i,j∈I，这样的马尔科夫链称为离散马尔科夫链。若一个离散马尔科夫链的状态空间是有限的，则它所有的转移概率可以组成一个马尔科夫转移概率矩阵：

(3)

1.2.2自更新马尔科夫链 原音乐信息中，音乐块是顺序出现的，所以在使用马尔科夫链进行状态转移时，除了最后一个音乐块可能会出现缺少下一个转移状态的情况外，其余每个音乐块至少都有一个转移状态。针对最后一个音乐块没有下一个转移状态的特殊情况，本研究利用音乐前后的相似性，将该音乐块前一个音乐块作为下一个状态自动更新马尔科夫链，并且为了避免生成音乐时进入死循环，观察前一个音乐块的转移状态数是否大于等于2，若小于2，则将此音乐块的前一个音乐块也作为一种转移状态更新马尔科夫转移矩阵，直到当前音乐块的前一个音乐块的转移状态数大于等于2为止。在原始音乐局部转移状态数较少时，也可使用该方法来丰富局部音乐块转移状态，以生成更好的音乐。

图2 自更新马尔科夫链原理Fig.2 Automatic updating Markov chain schematic diagram

2 耳鸣康复音乐合成方案

2.1 耳鸣康复音乐合成总体思路

音乐由一个或者多个声部组成，在独唱或者独奏中只有一个声部在发挥作用，而在合唱或者器乐合奏中乐曲由多个声部组成。然而在多声部中，通常只有一个演奏主旋律的声部，其他声部起伴奏作用。本研究在选取整首音乐后，都将第一个声部作为主旋律声部。首先,对MIDI音乐主旋律声部的音符、和弦进行编号,采用字符对编码将音乐分割成块；其次，利用这些音乐块来构造马尔科夫转移矩阵；最后，使用自更新马尔科夫链生成任意长度的满足耳鸣治疗需求的音乐。图3为本研究生成耳鸣康复音乐的流程图。

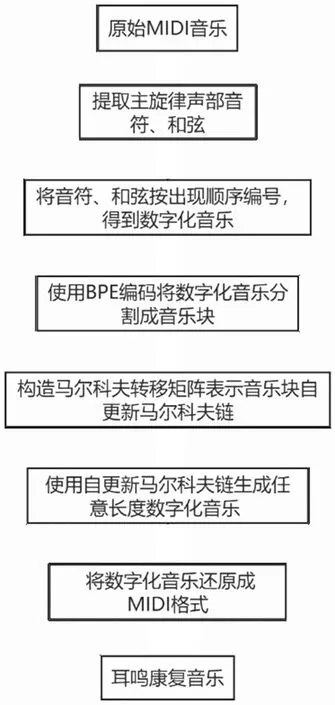
图3 耳鸣康复音乐合成过程

2.2 原始MIDI音乐处理

MIDI是一种标准化的数据格式，易操作且数据存储量小。因此，本研究选取的音乐皆为MIDI格式。本研究通过abcMIDI包，提取MIDI音乐主旋律声部的音符、和弦，将音符、和弦按照前后出现的顺序进行编号，并使用编号后的数字代替原音符、和弦，得到数字化后的音乐信息。

BPE最早用于数字压缩，目前在自然语言处理中多被用于分词。MIDI音乐由音符、和弦构成，音符、和弦在音乐中有一定的组成和顺序关系，而杂乱无章的音符和和弦无法组合成悦耳的音乐。因此，本研究利用BPE可不断统计迭代高频出现的字节对的特点，对数字化后的音乐信息中出现的高频音乐元素进行组合，将数字化后的音乐按照原有的顺序划分成音乐块。

以编号后的音符、和弦为例。将一小段音乐的音符、和弦按照前后出现顺序进行数字编号，并且使用编号后的数字代替原音符、和弦，得到一段数字文本：{3，3，3，28，16，3，3，3，28，3，10}。利用BPE进行编码的步骤为：设定BPE停止条件为相邻字节对最高出现次数不超过1，将单个数字作为子词，统计相邻子词出现次数，此时“3，3”出现频率最高，使用“-1”来代替“3，3”，文本变为：{-1，3，28，16，-1，3，28，3，10}，此时“3，28”出现频率最高，使用“-2”来代替“3，28”，文本变为：{-1，-2，16，-1，-2，3，10},此时“-1，-2”出现频率最高，使用“-3”来代替“-1，-2”，文本变为：{-3，16，-3，3，10}。最后，所有相邻子词的出现次数都为1，得到最终的文本数据：{-3，16，-3，3，10}。BPE解码时按照相反的顺序进行更新替换即可。

本研究对数字化后的音乐信息，统计其相邻数字出现的频率，将出现频率最高的数字对进行合并，替换成音乐信息中未出现过的数字，直到统计数字对的最高频率不超过设定阈值。实验表明，当阈值设置为1时，生成音乐的效果最好。

2.3 音乐生成模型构建

本研究使用马尔科夫转移矩阵描述生成音乐的自更新马尔科夫链。在马尔科夫转移矩阵中，将每个音乐块作为一种状态，实验中假设下一个音乐块出现的概率只和前一个出现的音乐块有关。

马尔科夫转移矩阵构建过程如下：首先，统计BPE编码后的音乐块种类N，并对音乐块按照出现顺序进行1至N编号，重复出现的音乐块编号和第一次出现的该音乐块编号一样。统计N种音乐块之间的转移频数，得到N种音乐块之间的转移概率。然后构建一个N×N大小的矩阵，矩阵最左上角元素为(1,1),矩阵元素(i,j)表示编号为i的音乐块转移到编号为j的音乐块的概率。观察此N×N大小的矩阵元素(N,N)的值是否为0。若为0，则使用自更新马尔科夫链的更新规则添加新的状态转移，并以此更新状态转移矩阵。最后得到生成的马尔科夫转移矩阵，随机选择一个音乐块作为开始，根据此马尔科夫转移矩阵生成任意长度的音乐(在耳鸣的临床治疗中，可根据患者的治疗时间来生成相应时长的对应音乐)。

2.4 使用MIDI技术合成音乐

首先，将马尔科夫链生成的任意长度的音乐进行BPE解码；然后，按照数字与原始音符、和弦的对应关系将数字还原成原始的音符、和弦；最后赋予这些音符、和弦和原始音乐一样的音乐信息，即音色、音符持续时间、音符速度等，如此便获得和原曲相似且任意长度的满足耳鸣治疗需求的音乐。

3 仿真结果及试听分析

3.1 仿真结果分析要素

本研究从1/f波动和分形两个角度对合成音乐进行客观分析。1/f波动分析表明，合成音乐能让人感到愉悦放松并具有较高的舒适感，音乐的分形分析表明，合成音乐具有相似不重复性，即合成音乐像人工创作的音乐一样具有前后自相似的特点[17]，能够避免唤醒耳鸣患者的记忆，以上分析表明，本研究合成音乐作为耳鸣康复音乐具有较强的合理性。最后通过试听分析，对合成音乐的听觉效果进行主观检验，表明合成的音乐流畅、自然。

3.2 音调值和音符时值1/f波动分析

1/f波动是一种具有舒适感的波动，可通过谱密度S(f)与频率f的关系表示，谱密度S(f)表示信号在频率f处的均方根变化。具体见式(4)：

S(f)∝f-β

(4)

对上式两边取对数，得到：

log(S(f))∝-βlog(f)

(4)

研究表明，大多数令人愉悦的音乐都是1/f波动，且几乎所有的音乐旋律都在模仿1/f波动，当0.5<β<1.5时，信号即满足1/f波动[18]。

图4是生成音乐的音调值和音符时值的功率谱拟合曲线，两个拟合曲线对应的β值分别是0.8987、0.9019，均在(0.5,1.5)范围内，即生成的音乐是一种舒适且可让人感到放松的1/f波动信号。

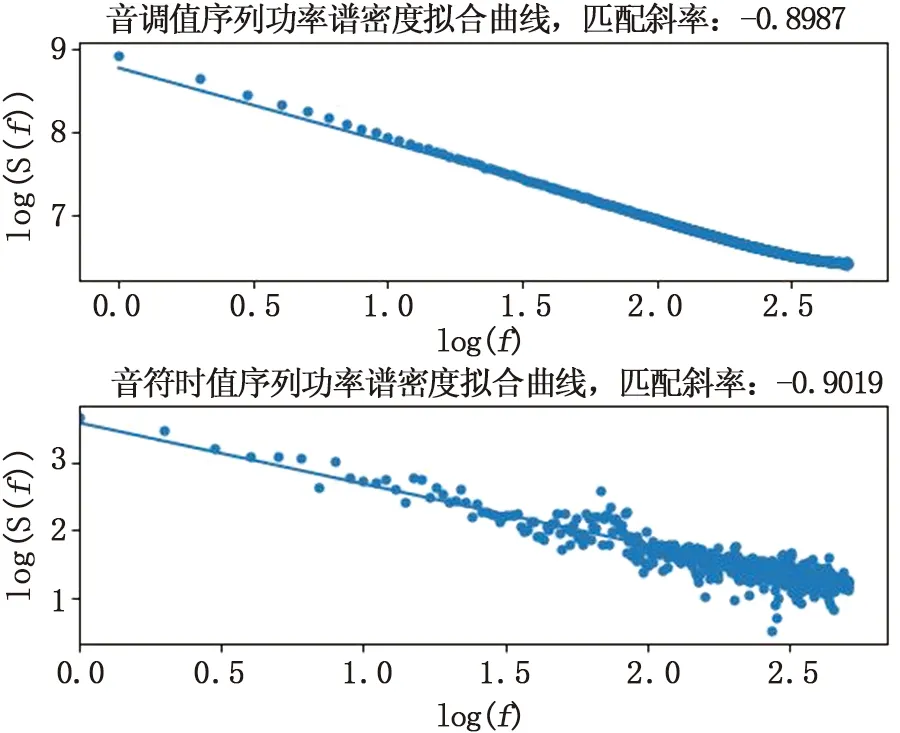
图4 音调值序列和音符时值序列功率谱密度拟合曲线

3.3 音乐分形分析

3.3.1分形维度分析 分形特征之一是自相似但不完全重复,即整体与局部的高度相似[19]，可以此检验合成的耳鸣康复音乐是否满足自相似、非重复的要求。在音乐中，相邻音符的音程i及其出现的频率F(i)若满足下述函数，则此关系称为分形。其中，C是常数，D是音乐的分形维度。

(6)

将上述等式两边同时取对数，得到：

logF(i)=C′-Dlogi

(7)

由此可知，logi和logF(i)是以-D为斜率的线性关系。

图5是本研究生成音乐中i与F(i)之间的对数关系的拟合曲线，可见，logi与logF(i)基本呈线性关系，斜率为-2.207。

图5 音乐分形结构分析

3.3.2旋律轮廓分析 旋律轮廓描述了旋律的整体形状，比准确的音程信息更容易认识与记忆。本研究使用音符作为最小单位来代表旋律轮廓。图6是生成较短时间的音乐的旋律轮廓，其中纵坐标是音符的音调值，横坐标是音符的序列值。图7是生成较长时间音乐的旋律轮廓。观察两段旋律轮廓可以看出，音乐旋律前后相似且旋律自然，生成的长时间音乐并非音符的简单重复。音乐的音高在一定范围内变化，未出现音高突变的情况。即生成的音乐满足相似且不重复的特性，无音高突变，满足耳鸣治疗音乐的要求。

图6 短时间音乐的旋律轮廓

图7 长时间音乐的旋律轮廓

3.4 试听分析

本次试听实验采用文献[16]和原始音乐拼接的音乐作为对照。假设一段2 min的音乐为耳鸣患者的偏好音乐，分别根据该原始音乐使用本研究和文献[16]的方法合成时长为30 min的音乐Frag_1、Frag_2，并将这段2 min的原始音乐首尾相连，拼接成30 min的音乐Frag_3。30名试听人员根据试听结果分别在相似不重复、重复、流畅、舒缓、与原曲最相似五项要素中选择出最符合该音乐特性的要素。其中，相似不重复和重复只能二选一，与原曲最相似这项要素，Frag_1、Frag_2之间只能选择一个，Frag_3不参与该项选择。流畅与舒缓全选、全不选、选其一皆可。

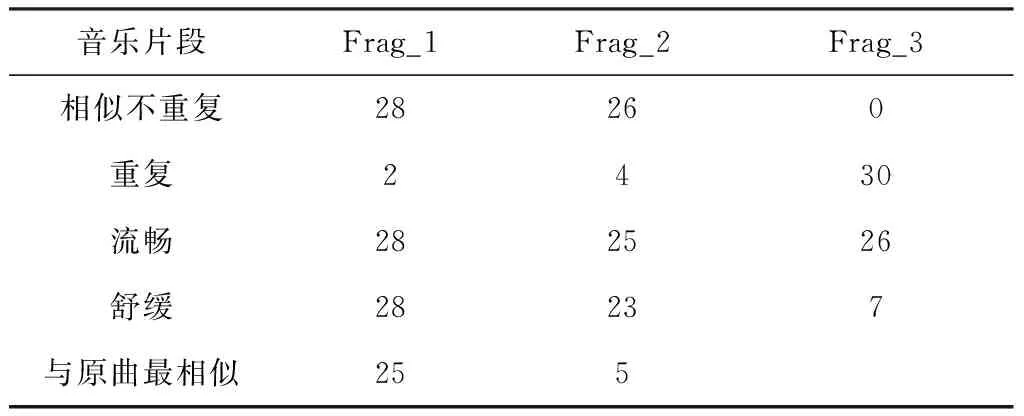
表1 音乐片段试听

试听结果表明，本研究合成的音乐具有令人舒缓、相似不重复的特性，与仿真结果相吻合。同时弥补了临床上需反复播放音乐，以及现有方法生成音乐不自然的缺陷。然而该试听结果是对耳鸣康复音乐的主观检验，还未完全应用到实际临床中，后续在临床中还需根据患者的具体情况调节相关参数，以达到更好的效果。

4 总结

本研究提出了一种基于BPE和马尔科夫链的耳鸣康复音乐合成新方法。该方法简单，可生成任意时长且适用于所有MIDI格式的音乐，便于临床上的推广。仿真及试听结果表明，该方法生成的音乐是一种能让人感到舒缓的1/f波动，在满足患者个性化偏好的同时，整体相似但不重复，弥补了临床上需重复播放有限时长音乐的问题，在听感体验上也更加流畅自然。因此，本研究提出的音乐合成方法对使用音乐疗法治疗耳鸣具有一定的借鉴意义。