基于单通道脑电信号中眼电伪迹去除的方法

徐雨，郑威，程怡

(江苏科技大学，镇江 212000)

引言

脑电信号[1]是一种极微弱的生理信号，采集过程中易受肌电伪迹和眼电伪迹等生理伪迹影响。由于眼电伪迹幅值较大且与脑电信号频率相近，对脑电信号产生很大干扰[2]，致使脑电信号产生畸变，影响分析结果。

为得到无干扰的脑电信号，国内外团队研究了多种去除眼电伪迹的方法[3-4]。其中，有研究认为在实验对象采集信号时不转动眼球，可避免眼电伪迹的产生，但实际情况中眼球活动不可控制，所以在脑电信号采集过程中仍会有大量眼电伪迹产生[5]。目前，独立成分分析(independent component analysis, ICA[6])、经验模态分解(empirical mode decomposition, EMD[7])等算法可有效去除眼电伪迹。其中，ICA算法只能处理单一的非线性函数[8]，去伪迹时需要人工识别伪迹成分。EMD可分解非线性和非平稳信号，但其在分解过程中存在模态混叠问题[9]。

针对EMD和ICA在去除脑电信号中眼电伪迹时存在的弊端，本研究提出了自适应噪声完整经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)、(kernel independent compoment analysis，KICA)[10]和样本熵相结合的方法用以去除脑电信号中眼电伪迹。该方法可以保留更多有用信息，更具有鲁棒性。

1 基本原理

本研究提出的眼电伪迹去除方法流程见图1。首先，对脑电信号进行带通滤波，对其进行自适应白噪声完整经验模态分解得到模态分量[11]；再对模态分量进行KICA降维；随后对得到的独立分量进行熵值计算，利用阈值判别并去除眼电伪迹，最后重构信号。

图1 去除脑电信号中眼电伪迹的流程图

1.1 CEEMDAN算法

EMD分析时频分布的能力较强，但在分解过程中会存在模态混叠问题。为解决此问题，王海龙等[12]提出在EMD中加入白噪声的EEMD算法。但EEMD[13]不具有完备性，通过对EEMD分解后的经验模态分量自适应地加入白噪声，解决了EEMD分解中无完备性的问题。

CEEMDAN算法的步骤具体如下：

(1)构造加入噪声的序列：xi(t)=x(t)+ω0εi(t),i∈{1,2,…,I}，其中，x(t)为观测信号，εi(t)为独立的方差为1的高斯白噪声，ω0为噪声的标准差。最后得到的模态分量记为cq(I).

(4)设分解Q层，得出每个阶段第q个剩余分量和第q+1个模态分量(q=1,…,Q-1)，再次进行步骤(2)的计算：

1.2 核独立成分分析

ICA算法是基于非线性函数期望值的一个固定形式[14]，由于对比函数的局限性，导致处理更复杂的非线性形式的盲源问题时，精确度低[15-16]。KICA在ICA基础上引入核函数[17]，其使用的函数空间适用于各种不同分布的源。与ICA相比，KICA具有更好的分离能力和更好的鲁棒性[18-19]。

KICA算法的步骤如下[20]：

(1)输入样本集A=(a1,a2,…aI)，xi∈Rn，i=1,2,…，I，利用核函数代替向量的内积，并对数据进行白化处理。

(2)中心化数据。

(3)将RKHS中的非线性函数用作比较函数。

(4)最小化比较函数,输出分离矩阵W。

1.3 基于熵的伪迹判断

样本熵算法是一种判别时间序列复杂程度的算法[21-22]。与脑电信号相比，眼电信号比较规律，对应熵值较低，通过熵值的判别可以去除熵值较低的眼电伪迹成分。与近似熵相比，样本熵[23]的计算对数据长度要求低，且具有更好的稳定性[24]。样本熵的计算如下：

(1)设长度为P的观测信号为{a(i),1≤i≤P}，即可得到一组e维的矢量:Ae(1),…,Ae(P-m+1)，其中Ae(i)={a(i),a(i+1),…,a(i+e-1)},1≤i≤P-e+1。其中，e为相空间维数。

(2)定义d[Ae(i),Ae(j)]为向量Ae(i)与Ae(j)之间的距离最大差值的绝对值。

(4)增加维数到e+1，循环步骤(1)到(3)，同理得到Ve+1(r)。样本熵为：

(5)若N为有限值，样本熵可为：

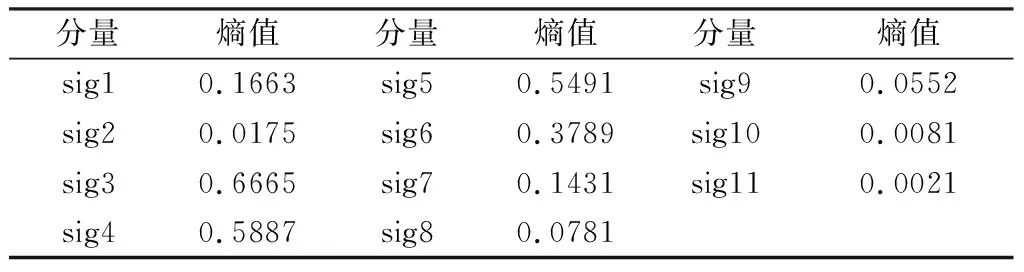
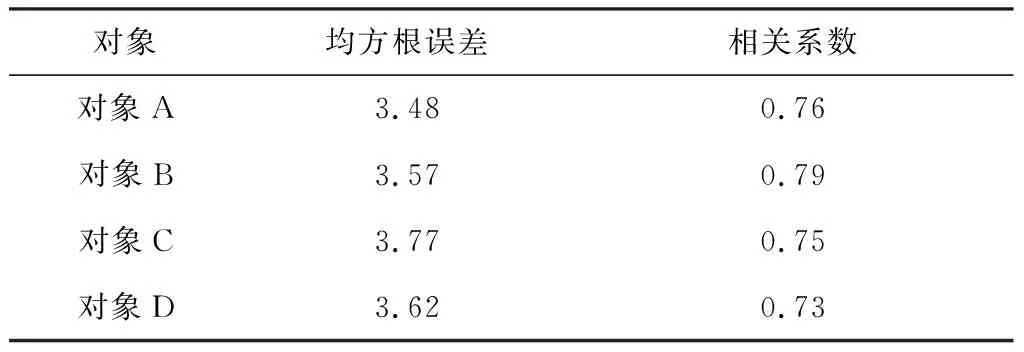
式中：o为相似容限。本实验运用Gomez-Herrero提出的阈值判别式[25]识别伪迹。首先，定义变量c满足1

φ(c+1)-φ(c)<φ(c)-φ(c-1)

(1)

式中，φ(c)表示KICA得到的独立分量升序排序后的第c个分量的熵值，定义[P/2]为不大于P/2的最大整数。

若存在变量c满足上述条件，c取满足条件的最小整数，则φ(c)为独立分量阈值，由于眼电伪迹的熵值比脑电信号的熵值更低，因此，判定排序前c个熵值对应的分量为眼电伪迹，对其进行置零。

2 实验

2.1 实验数据来源

本实验脑电信号采用BCI Competition IV的Data sets 2b 的数据集。实验对象为四名健康人员，采样频率250 Hz。实验对象都是右利手，有正常或者矫正正常视力。实验采集分为三个部分：(1)2 min睁眼和1 min闭眼(2)眼电信号采集(3)脑电信号采集。

由图2可知，对象A的脑电信号中800和1 500采点处存在眼电伪迹信号；对象B的脑电信号中1 200采点处存在眼电伪迹信号；对象C的脑电信号中220采点处存在眼电伪迹；对象D的脑电信号中220、1 750采点处存在眼电伪迹。

图2 含有伪迹的原始脑电信号

2.2 实验步骤

本实验具体步骤：

(1)对滤波后的脑电信号进行自适应白噪声完整经验模态分解。

(2)通过核独立成分分析，对模态分解得到的模态分量进行分析，得到核独立分量。

(3)对独立分量进行样本熵计算，利用阈值判别式判别眼电分量，若为伪迹，则将其置零去除。

(4)对去除伪迹后的信号进行核独立成分分析逆变换，随后对逆变换后的信号进行叠加，最终得到去除伪迹后的脑电信号。

图3为自适应白噪声完整经验模态分解后得到的分量图。

图3 CEEMDAN分解得到的模态分量Fig.3 The modal components obtained by CEEMDAN decomposition

核独立成分分析获得的分量见图4。对图4所得的各个分量进行熵值计算，所得熵值见表1、表2、表3、表4。

表1 对象A的各分量的熵值

表2 对象B的各分量的熵值

表3 对象C的各分量的熵值

图4 核独立分量Fig.4 Kernel-independent components

表4 对象D的各分量的熵值

通过阈值判别式(1)，可以判定表1中，sig2、sig10、sig11、sig12属于眼电伪迹；表2中，sig2、sig9、sig10、sig11属于眼电伪迹；表3中，sig2、sig9、sig10、sig11；表4中，sig2、sig10、sig11、sig12属于眼电伪迹，将眼电伪迹成分置零。脑电信号中眼电伪迹去除前和去除后的效果对比图，见图5—图8。

图5 对象A的眼电伪迹去除前后对比图

图6 对象B的眼电伪迹去除前后对比图

图7 对象C的眼电伪迹去除前后对比图

图8 对象D的眼电伪迹去除前后对比图

2.3 实验结果及分析

本研究通过均方根误差(RMSE)和相关系数(R)来判别去除伪迹的效果，其公式如下：

式中：x和y分别表示初始脑电信号和伪迹去除后的脑电信号。实验对象A、B、C、D的RMSE与相关系数见表5。本研究选取对象A的数据来作为参考分析数据，对其进行15次实验，取实验结果的平均值。为证实本方法的有效性，与KICA、CEEMDAN-FastICA两种方法进行对比，结果见表6。

表5 各实验对象的RMSE和相关系数

表6 各算法RMSE和相关系数

由表6可知，CEEMDAN-FastICA方法的相关系数最小，说明FastICA在分析信号时可能受外界影响，分离能力下降，使眼电伪迹未得到有效去除，最终重构得到的脑电信号与原脑电信号相差较大。而CEEMDAN-KICA方法RMSE最小，相关系数最大，说明KICA较好地解决了非线性混合信号的问题，并且重构后的信息误差较小，且能够较好地保留有用的数据信息。

3 结论

本研究提出CEEMDAN和KICA相结合的眼电伪迹去除方法，首先，对脑电信号进行模态分解，再对分解后得到的模态分量进行核独立成分分析，得到独立分量，随后对独立分量进行样本熵计算，利用阈值对熵值进行判别，将眼电分量置零，最后重构去除伪迹后的信号。通过实验表明，本研究提出的眼电伪迹去除方法更准确，能有效去除眼电伪迹，更具有鲁棒性。