基于Tree-3决策树模型的大数据挖掘算法

褚福洋 马文辉 张文晶 闫继伟

（齐齐哈尔医学院，黑龙江 齐齐哈尔 161006）

大数据时代为人们提供了信息量十分庞大的数据集合，为人们找到更有用、更有效的信息提供了可能[1]。但是，如何从海量数据中检索自己所需要的有价值的信息也成为一项技术难题。数据挖掘算法就是解决该问题的有效技术途径[2]。数据挖掘算法具备对数据进行整理、归类、分析和提取等作用，其实质是在机器学习的基础上进行聚类、关联分析的方法[3]。基于决策树的数据挖掘方法在数据挖掘领域具有十分重要的地位。其中，Tree-3 决策树模型在这类方法中具有重要意义。该文在Tree-3 决策树模型下，针对其存在的不足进行改进，构建更适合大数据挖掘的算法。

1 Tree-3决策树模型及其挖掘算法流程

Tree-3 决策树模型在各种决策树挖掘算法模型中是最经典的一种模型。在常规的决策树的构建过程中，Tree-3 决策树模型使用了一种新的名为信息熵浓度增加-判定的机制，沿着决策树路径按节点进行搜索，搜索依据就是信息熵浓度更高的节点被保留，当搜索遍历整个决策树时，搜索过程被执行完毕，所需的检索结果被找出。

假定参数是 一个论域，并且对它随机执行一个划分{M1，点，这个根节点的信息熵计算如公式（4）所示。M2，…，Mn}，可以得到的概率分布Pi=P（Mi），这样M的信息熵计算如公式（1）所示。

在大数据挖掘的过程中，可以采用T和F表示符合要求和不符合要求的数据样本，，据此可以得出有关2 类样本分类的信息熵，如公式（3）所示。

在数据挖掘过程中，用户特别要求的属性A将成为根节

包括属性A的根节点信息熵浓度的增加部分可以按照这样的方式进行计算，如公式（5）所示。

Tree-3 决策树模型构建的数据挖掘算法的目标就是在整个决策树中找到符合用户属性要求并且信息熵浓度增益最大的那个节点作为根节点。基于Tree-3 决策树模型的数据挖掘算法流程如图1 所示。

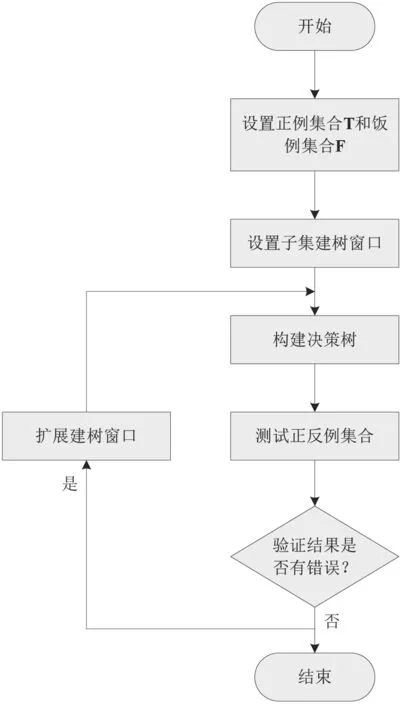
图1 基于Tree-3 决策树模型的数据挖掘算法流程

由图1 可知，执行的各个环节如下：1）根据用户的检索需求，在大数据全部样本中确定符合要求的样本集合和不符合要求的样本集合。2）根据用户的检索需求，设定检索过程中的关键属性，关键属性可能是1 个，也可能是多个，根据这些属性构建关键属性集合，从而制定属性信息熵浓度增加的计算规则。3）根据Tree-3 决策树模型的信息熵浓度增加规则进行计算，并由此构建决策树。4）每执行1 个关键属性元素进行信息熵浓度增加计算就得到1 个决策树，得到全部属性决策树后，比较各个决策树的根节点信息熵浓度的大小，信息熵浓度最大的为最终胜出者，其检索路径和结果作为数据挖掘结果输出。

2 基于Tree-3决策树模型的改进算法

基于Tree-3 决策树模型构建的数据挖掘算法原理简单、执行思路清晰且算法硬件计算量消耗小，对很多领域的数据挖掘都具有较高的适用性。但是，基于Tree-3决策树模型构建的数据挖掘算法在关键属性确定出现偏差时，就会出现无法得到全局最佳结果的问题，即最终推送给用户的挖掘结果可能是次优的或者是局部最优的结果。

因此，该文对基于Tree-3 决策树模型建构过程进行改进，以期得到准确推送全局最优挖掘结果的数据挖掘方法。Tree-3决策树模型的挖掘依赖信息熵浓度增加的判定，并由此确定关键属性。因此，要解决Tree-3 决策树模型的问题，就需要改进信息熵浓度的计算方法。而用户的检索要求可能涉及多个属性，为了更准确地确定关键属性，该文结合各属性概率特征，重新修定Tree-3 决策树模型的信息熵计算过程。

如果一个属性A包括m个子值，并且这些属性子值的概率分别为p1、p2、…、pm，那么Tree-3 决策树依托属性A构建就可以为包括m个子节点的集合{θ1，θ2，…，θm}，进一步用G（θ1）、G（θ2）、…、G（θm）表示各属性子值的信息熵，就可以计算属性A的信息熵，如公式（6）所示。

基于Tree-3 决策树模型的改进算法的流程如下：1）如果用户检索要求的一个属性为Ai，并且其包括mi个子值，那么子值属性集合为{θ1，θ2，…，θm i}，集合中各元素对应的概率为p1、p2、…、pm i，那么可以得到集合中一个子值的信息熵，如公式（7）所示。2）根据公式（6）并结合全部子值信息熵计算Ai的信息熵。3）重复上面2 个步骤，得到用户检索要求的全部属性的信息熵，并以信息熵浓度增加最大的属性为该节点的属性。4）根据前3 个环节遍历决策树所有节点，确定各个节点的属性，并得到每个节点的属性信息熵增益浓度。5）将信息熵浓度最大的节点确定为根节点，并将其输出作为挖掘结果。

3 基于Tree-3决策树模型的改进算法的数据挖掘试验

3.1 大数据集合的选取

在大数据挖掘算法的验证试验中，领域内的常规做法是用国际公认的标准数据集进行挖掘算法验证试验，这样便于形成横向比对。该文从国际通用的UCI 数据集合中选择6 个数据子集进行挖掘试验。这6 类数据子集分布领域如图2 所示。

图2 6 类数据子集的分布领域

3.1.1 UCI-Wine 数据子集

在UCI-Wine 数据子集中，全部是有关白酒行业的各种数据，包括白酒的各种关键参数。在UCI-Wine 数据子集中，纳入了全球180 多 个知名品牌的白酒，涉及的关键参数包括这些品牌白酒中的酒精参数、果酸参数以及黄酮参数等信息。

3.1.2 UCI-Heart 数据子集

UCI-Heart 数据子集全部是心脏扫描图像的各种数据，包括心脏是否患病的判断规则参数。在UCI-Heart 数据子集中，涉及270 多 个心脏类疾病的检索样本，涉及的关键参数包括对应疾病的各种体质性指标。

3.1.3 UCI-Balance 数据子集

UCI-Balance 数据子集全部是心理学意义上的心态是否平衡的样本数据，包括630 多 个各种可能情况下被测人员可能发生心理失衡的样本，这些样本中也涉及被测人员心理学意义上的各种指标。

3.1.4 UCI-Vehicle 数据子集

UCI-Vehicle 数据子集全部是有关汽车行业的各类数据，包括汽车的各种关键参数。在UCI-Vehicle 数据子集中，纳入了全球820 多 个知名品牌的汽车，涉及的关键参数包括这些品牌汽车中的发动机参数、排放参数以及稳定性参数等。

3.1.5 UCI-Valley 数据子集

UCI-Valley 数据子集全部是多顶点曲线连接的相关数据，包括顶点信息和连线信息。在UCI-Valley 数据子集中，纳入了1 200 多 个样本，为多顶点曲线连接集合形状的分类判别提供了依据。

3.1.6 UCI-Yeast 数据子集

UCI-Yeast 数据子集全部是细胞内蛋白质含量的各种数据，包括细胞是否正常的判断规则参数。在UCI-Yeast 数据子集中，涉及1 500 多 个细胞类疾病的检索样本，涉及的关键参数包括对应疾病的各种体质性指标。

上述6 个数据子集在样本数量、属性各属以及分类类别等各方面的基本情况对比见表1。

表1 数据挖掘试验中6 个数据子集的基本情况

3.2 Tree-3决策树模型及其改进方法的挖掘结果对比

根据表1 中提供的6 个数据集合，该文分别采用Tree-3决策树模型数据挖掘方法、基于Tree-3 决策树模型的改进数据挖掘方法进行试验，从而得到2 种挖掘方法得到的决策树的节点与最终的挖掘精度方面的对比，结果见表2。

表2 Tree-3 决策树模型及其改进方法的试验结果对比

由表2 可知，2 种方法得到的决策树节点总数柱状图对例如图3 所示。

图3 Tree-3 决策树模型及其改进方法的决策树节点总数对比

在图3 中，2 个颜色的柱状图分别表示基于Tree-3 决策树模型的大数据挖掘算法和该文提出的基于Tree-3 决策树模型的改进大数据挖掘算法。6 组试验结果的柱状图逐次降低，这也体现了6 个数据集的复杂程度的改变。其中，第一组数据集构建的决策树节点为338 个，对应的改进算法构建的决策树节点为249 个。到了最后一组数据集，决策树节点为57 个，而对应的改进算法构建的决策树节点为34 个。根据对比可以明显看出，经过该文的改进处理，Tree-3 决策树模型的结构更精简。而从挖掘精度上来看，如果决策树的模型复杂，那么Tree-3 决策树模型的挖掘精度就会明显降低。而该文改进的Tree-3 决策树模型的挖掘精度不会随着决策树模型的结构出现明显的改变。由图3 可知，对6 个UCI 数据子集来说，该文提出的改进方法比原有的Tree-3 决策树模型挖掘方法所构建的决策树的节点更少，结构更精简。

根据表2 中的试验结果可知，2 种方法得到的挖掘精度节曲线图对例如图4 所示。

从图4 可以看出，对6 个UCI 数据子集来说，该文提出的改进方法比原有的Tree-3 决策树模型挖掘方法的数据挖掘精度更高，可以为用户提供更准确的挖掘结果。

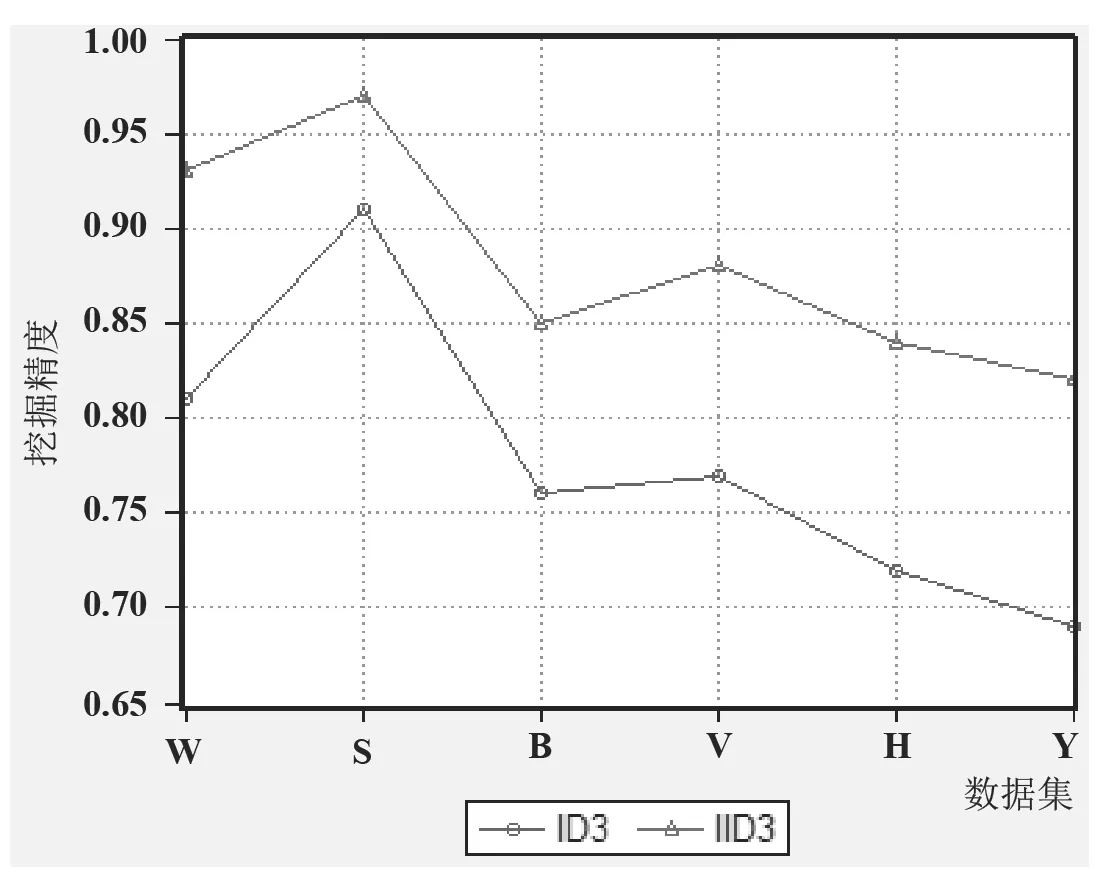
图4 Tree-3 决策树模型及其改进方法的挖掘精度对比

4 结语

大数据时代在为用户提供便利的同时，也带来了数据检索速度慢、检索准确率低的问题。因此，该文在Tree-3 决策树模型的基础上进行改进，提出了一种新的数据挖掘算法。首先，给出了Tree-3 决策树模型的建构方法。其次，针对Tree-3 决策树模型有时无法给出全局最优结果的问题，提出了信息熵改进计算方案，并给出了改进方法的具体流程。最后，对6 个UCI 数据子集进行挖掘试验，该文提出的改进方法可以得到更精简的决策树，还可以得到更高的挖掘精度。