基于信号整数抽取的频谱细化算法在直升机振动信号分析中的应用

龚明程 张学薇 张树桢

（航空工业直升机设计研究所，天津 300000）

0 引言

在旋转机械健康监测和故障诊断中，需要关注的频谱分量往往集中在一个狭窄的频带内，例如拍振信号就是一种典型的密集频率信号[1-2]。通常情况下，直升机的旋翼转速是比较稳定的，也可以看成集中在窄带的频率。由于受计算机内存和计算能力的限制，因此现实中会选择1 段局部信号进行FFT 变换，该方法以频谱分辨率为代价，减少了频谱分析中所需信号的样本数量，提高了分析效率。因此，既能获得高质量频谱分辨率，又比完整信号FFT 变换耗时少、效率高且计算量小的信号分析方法在工程中是必要的。

针对密集频率成分的识别问题，专家们已经提出多种频谱细化和校正方法，常见的方法有线性调频Z 变换法[3]、FFT+FS 法[4]和复调制频谱细化法（ZOOM-FFT）等。其中，ZOOM-FFT 法具有计算精度高和速度快的优点，适用于FFT变换点数不多的情况[5-6]。基于以上思路，该文提出了一种高效的区分信号密集频率成分的算法，并从数学上完整证明了该方法的原理。在同等处理器计算能力瓶颈的限制下，该方法的频谱质量比普通FFT 更高，得到工程中所关心频率附近的高精度频谱。

1 基于信号整数抽取的频谱细化算法简介与原理

1.1 信号整数抽取的频域特性

设有1 个无穷离散序列x（n），其中n∈Z，则用正整数D抽取该序列在时域上的表现为y（n）中每隔D-1 个抽样点抽取1 个样点，然后按次序组成序列x（n），该过程可用数学表达式描述，如公式（1）所示。

构造1 个序列z（n），该序列由脉冲序列和序列x（n）相乘而来，如公式（2）所示。

式中：i为整数；n为整数。

显然，序列x（n）、y（n）和z（n）在时域上的关系如公式（3）所示。

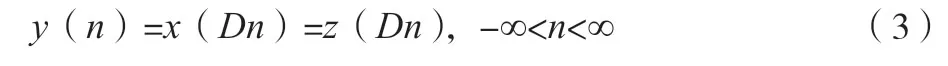
设x（n）、y（n）和z（n）的抽样频率分别为fx、fy和fz，可以得到公式（4）。

对各自抽样频率归一化的数字频率变量ωx、ωy和ωz来说，可定义如公式（5）所示。

则3 个数字频率变量由公式（6）关联。

对y（n）做离散时间傅里叶变换（DTFT），如公式（7）所示。

式中：j为虚数单位；z（m）为构造的序列；Z为进行离散时间傅里叶变换后的频谱函数。

由文献[7]和文献[8]可知，冲激函数具有尺度变换和取样特性，如公式（8）所示。

式中：a为非零实数；δ为冲击函数；q（t）为一个在t=t0处连续的普通函数。

利用公式（8），结合只有当i=0 时，ω-2πi才能落在[-π，π]的积分区间的特性，可得到恒等式，如公式（9）所示。

c（n）又可以为公式（11）。

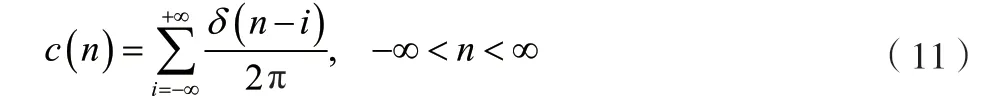
根据离散时间傅里叶变换成对的性质，又可得到恒等式，如公式（12）所示。

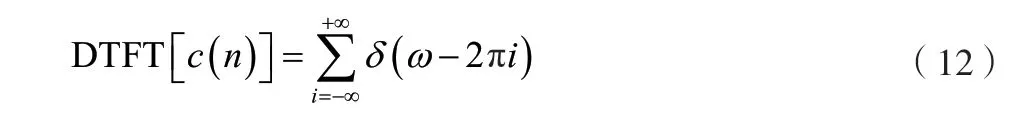
另一方面，直接对c（n）进行DFTF 变换，如公式（13）所示。

联立公式（12）和公式（13），可以得到公式（14）。

对z（n）进行DTFT 变换，如公式（16）所示。

式中：k为正整数。

将公式（16）和公式（6）代入公式（7），得到公式（17）。

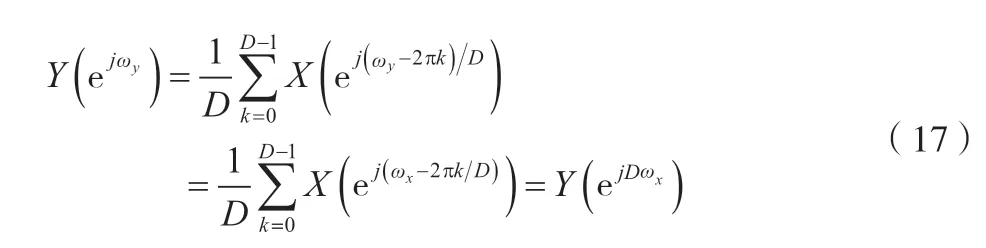
式中：y（ejωy）为频谱函数。

先从ωx的角度观察公式（17），Y（ejDωx）是先将y（ejωx）依次以0、2π/D、…、2（D-1）π/D为长度沿坐标轴ωx向右进行平移，然后再将每次平移后频谱函数的幅值相加起来乘以1/D而得出的。再从ωy的角度观察，Y（ejωy）可以理解为Y（ejDωx）顺频率轴扩展D倍。以D=3 为例，上述整个过程如图1 所示，图1（a）～图1（c）为产生混叠的情况，图1（d）～图1（f）为不产生混叠的情况，因此，抽取前必须加上防混叠低通滤波器。

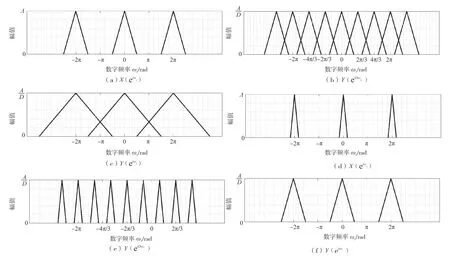
图1 初采样序列和再抽取序列的频谱（D=3）

由于Y（ejωy）的周期性，因此可以仅考虑单周期ωy∈[-π，π]，则ωx∈[-π/D，π/D]。此时只有k=0，X（ej（ωx-2πk/D））才会有意义，因此也只需要对其进行取k=0 的单周期分析，公式（17）变为公式（18）。

离散时间序列DTFT 变换后的结果是关于频率的连续函数，无法使用计算机处理，必须利用DFT 变换对其频域进行离散化，由于工程实际中的信号均为有限长信号，因此可以设采样后的有限序列为x1（lx），lx=0，1，2，…，N，即x1（lx）为无穷离散序列x（n）的一部分，则x1（lx）用正整数D抽取后的序列y1（ly）为公式（19）。

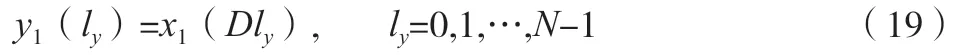
根据文献[9]可知，序列x1（lx）的 DFT 和x（n）的DTFT变换之间的关系、序列y1（ly）的 DFT 和y（n）的DTFT 变换之间的关系如公式（20）所示。

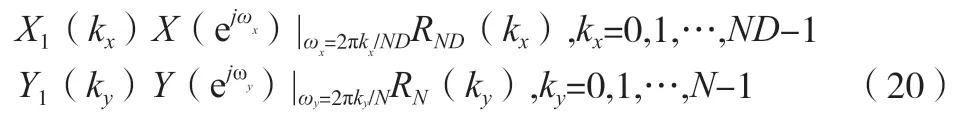
式中：RND（kx）和RN（ky）为矩形序列。

将公式（20）代入公式（18），并进行如公式（21）所示的变形。

由公式（21）可知，Y1（ky）的N条谱线和X1（kx）中的前N条谱线是完全相等的。因此，可以通过抽取后的信号y（ly）去间接求解原始信号的频谱，并且抽取后的信号的长度缩短，以较少的DFT 变换点数得到了原始信号的频率分辨率。

值得注意的是，为了保证降重抽取后的信号不产生混叠失真，需要在抽取前加上防混叠低通滤波器，由文献[10]和文献[11]可知，防混叠低通滤波器的理想频率响应Hd（eiω）须满足公式（22）。

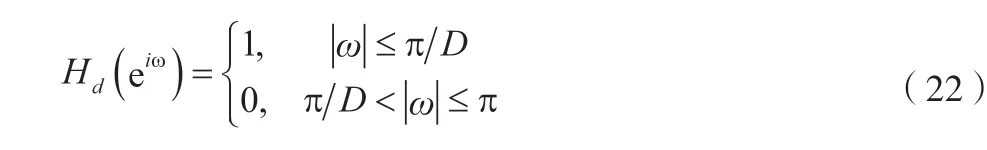
该文提供了2 种抽取数字滤波器设计方法，第一种方法基于Butterworth 生成IIR 低通数字滤波器，通带最大衰减As、阻带最小衰减Rp、归一化通带频率和归一化阻带频率4 个参数的取值如公式（23）所示。

根据Butterworth 滤波器的幅度平方函数可以求解滤波器阶次L和归一化截止频率，计算方法如公式（24）所示。当D=10 时，第一种方法对应滤波器的幅值响应曲线如图2 所示。

图2 Butterworth 低通滤波器幅值响应（D=10）

第二种方法是直接利用MATLAB 自带的resample 函数进行抽取，该函数内置FIR 抗混叠低通滤波器，并补偿滤波器带来的延迟。因此，使用resample 函数可以进一步提高程序的运行速率。

1.2 离散傅里叶变换的频域循环移位特性

设有限长度的离散时间序列为p0（n）（其中，n=0，1，…，N-1），采样频率为fs，则该序列的N点DFT 如公式（25）所示。

同时，谱线间隔记为∆f，实际需要细化分析的频带区间记为[fl，fu]，频带中心频率记为fe。由于细化分析时需要将中心频率fe移频至频率轴的零点，不妨先假设频谱P0（k）向左循环位移M个样点后，中心频率刚好移频至频率轴的零点，此时的频谱可记为P（k），如公式（26）所示。式中：（k+M）N为对k+M进行模N运算。

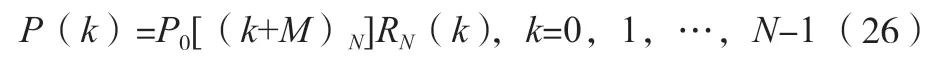
将公式（26）带入逆离散傅里叶变换IDFT，如公式（27）所示。

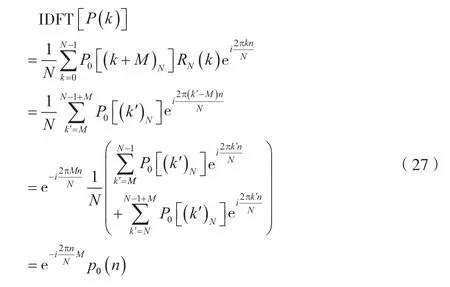
因此，中心频率fe刚好移频至频率轴的零点，等价于用e-i2πMn/N对原序列P0（n）进行复调制。参数M由fe在原频谱P0（k）中的位置来确定，取值如公式（28）所示。

1.3 算法的程序步骤

1.3.1 输入控制参数

信号和分析参数：原始信号为x（n）；信号采样频率为fs；FFT 变换点数为nfft。

IIR 低通滤波参数：通带最大衰减为As；阻带最小衰减为Rp。

1.3.2 确定细化参数

计算需要细化分析的频带中心频率fe。对信号x（n）做点数为nfft的FFT 变换，得到频率分辨为∆f=fs/nfft的频谱，确定需要细化分析的频带区间[fl，fu]，计算中心频率fe，如公式（29）所示。

确定最大细化倍数D。根据奈奎斯特抽样定理可知，细化倍数（整数抽取因子）D的选取理论上只需要满足公式（30）。

考虑当设计的低通滤波器在|ω|∈[π/2D，π/D]的过渡带时，实际频率响应Hd（eiω）存在衰减，即理论上计算的细化频带区间[fe-fd/2，fe+fd/2]中只有[fe-fd/4，fe+fd/4]区间的幅值是真实的。可以通过强化约束细化倍数的判断公式（30）解决该问题，公式（30）修正为公式（31）。

公式（30）可以理解为判定2 倍细化倍数后的理论细化频带是否包括需要细化分析的频带[fl，fu]。显然，这种保守做法可以确保需要细化分析频带区间幅值的真实性。为了满足正整数抽取的要求，可以根据公式（32）求解最大细化倍数。

式中：floor 为向下取整函数。

设计低通滤波器：计算归一化通带频率ωp和阻带频率ωs，基于Butterworth 模拟滤波器生成IIR 低通数字滤波器。

1.3.3 时域复调制

将中心频率fe移频至频率轴的零点，先计算抽取/调制需要用到的点数ndec，由于频域循环位移等价于对序列x（n）进行时域复调制，因此调制后x（n）变为复数信号x1（n），如公式（33）所示。

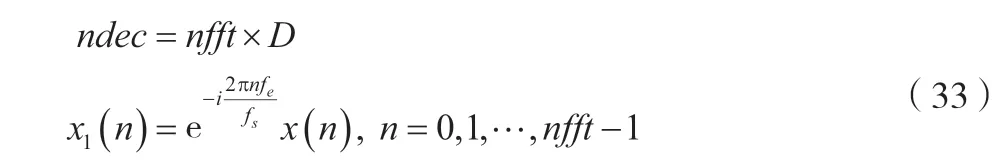
1.3.4 降重抽取

按照正整数因子D进行抽取。经过复调制和低通滤波后，信号频带变窄，然后再对其进行x1（n）抽取，等价于用较低的采样率fdec对x1（n）进行重采样，如公式（34）所示。

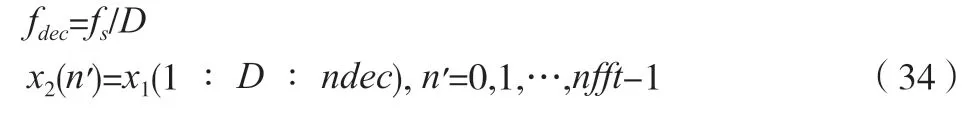
1.3.5 频域调整

FFT 变换。对抽取后的离散序列x2（）进行点数为nfft的复数FFT 计算，频谱记为X2（k）。

幅值修正和翻转。fftshift 函数为MATLAB 内置函数，作用是将0 频率分量移到频谱中心，如公式（35）所示。

频率刻度恢复。重采样后的频率分辨率如公式（30）所示，比第一次的分辨率提高了D倍，如公式（36）所示。

细化再迭代。如果细化后的频谱分辨率仍不理想，重就复步骤2、3、4 和5，直至达到目标频谱精度。

2 仿真算例

以下2 个算例均在8 核16 线程CPU、3.2 GHz 主频和16 G内存的计算机上进行计算。

2.1 含多个密集频率成分的频谱细化分析

设1 个加速度仿真信号由5 个不同频率的正弦信号构成，幅值均为1，初始相位均为0，频率分别为100.047、100.049、100.050、100.051 和100.054，并添加均值为0、方差为1 的高斯白噪声，信号的采样频率为2 000 Hz，单位为m/s2。

仿真算例中的FFT 变换点数取为2 048，经过6 次频谱细化迭代后可精确识别5 个非常靠近的窄带频率，最大误差为0.000 008 Hz，准确率极高，需要细化倍数和频带区间的设置见表1，每次细化后的频谱如图3 所示。如果传统方法要达到的同样的精度，就需要进行点数为2048×50000 的FFT 变换，对计算机性能的要求较高，而该文提出的方法只需要进行点数为2 048 的FFT 变换，极大地降低了对硬件内存和处理器性能的要求。

表1 仿真信号6 次细化参数和频谱

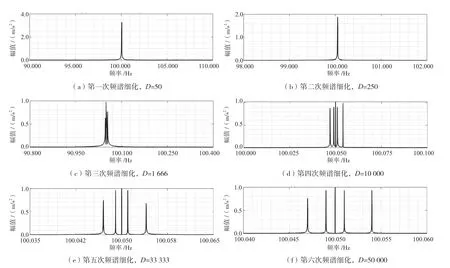
图3 仿真信号的细化频谱

2.2 直升机振动信号的频谱细化分析

某型民用直升机在某次试飞试验中，500 s～2 500 s 的右驾驶员座椅地板处加速度信号和旋翼转速Nr 百分比信号如图4 所示，加速度信号采样率为1 024 Hz，以重力加速度g为基本单位，Nr 信号采样率为25 Hz，单位为百分比。已知Nr=100%时的旋翼一阶通过转速频率为23.65 Hz。

图4 驾驶员座椅地板振动信号和旋翼转速信号

该算例利用该文提出的算法准确提取直升机的旋翼一阶通过频率。其中，细化参数按照如下方法设置，FFT 变换的点数为1 000，细化倍数D=2 000，细化频带取[23.03，23.28]，则细化后的频谱如图5（a）所示，最高峰对应的频率为23.151 5 Hz。另外，Nr 信号也是离散点，通过统计的方法计算Nr 的每个值出现的次数，最后再除以500 s～2 500 s 期间Nr 信号的总长度，得到Nr 的每个值在500 s～2 500 s 飞行中出现的概率，也可以理解为Nr 的概率密度分布，如图5（b）所示，出现次数最多Nr 对应的频率为23.148 3 Hz。图5（a）和图5（b）中的峰值对应的频率相差0.003 2 Hz，再次验证了该文提出的算法具有非常高的精度。

图5 驾驶员座椅细化频谱和旋翼转速概率密度分布

3 结语

该文提出的基于信号抽取性质的频谱细化算法，一方面降低了需要分析的信号长度，等价于降低对FFT 变换的点数的要求，降低了对处理器硬件的要求，变相提高了分析效率；另一方面，如果采用之前FFT 变换的点数，在不改变计算机硬件性能的情况下，可以提高关心频带区间的频谱分辨率，极高的精度优势是传统FFT 分析方法无法比拟的。

借鉴第二个算例，该文提出的算法还可以进一步拓展到直升机排故中，先通过传统FFT 方法分析故障频率的大概范围，然后再用该文提出的算法逐步对关心频带进行细化分析，也可以为精准定位和进一步分析异常振动源头提供依据。