铁路路基翻浆冒泥的参数敏感性及不确定性分析

王 威，杨文豪，杨成忠，吴宇健，郑明新

(1.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013；2.华东交通大学 交通运输工程学院，江西 南昌 330013)

铁路作为国家主要的基础设施之一，在综合交通运输体系中占有极高地位，为我国国民经济的迅速发展做出重大贡献。但随着我国铁路大量修建，多数铁路在投入运营后，因客、货运量日益增多，加上地质复杂、自然灾害等的影响，导致线路局部路段时常出现边坡坍塌、翻浆冒泥、道砟陷槽等病害，严重影响铁路运输安全。大量工程实践表明，翻浆冒泥是铁路路基中出现频率最高的病害之一[1-6]，该病害不仅会增加线路的维修工作量，而且会引起基床软化，导致基床弹性降低，影响列车长期运行的安全性和稳定性[7-8]。目前，铁路线路上预防维修翻浆冒泥是通过巡线观察[9-10]、轨检车检测[11-12]和GPR勘探[13-14]等方法，而后根据检查结果制定相应的维修计划。虽然上述方法在一定程度上能达到预期的效果，但容易受到诸多因素的影响，如测速慢、测试时需花费较长的时间成本等，使得预防翻浆冒泥错过最佳时间[15]。因此，为准确有效的控制与预防路基翻浆冒泥，对其发生的可能性进行合理的评估尤为重要。

通常情况下，翻浆冒泥病害的产生受多方面因素的影响，如水文、气候、道砟层厚度、路基服役时间等，且在普铁线路中更易出现。因此，明确翻浆冒泥形成的机理对提高预防该病害发生的效果具有重要意义。目前，关于铁路路基翻浆冒泥发生机理的研究，多数学者采用室内模型试验、现场测试与数值模拟相结合的方式对翻浆冒泥的影响因素进行研究，认为土质不良、水和列车动载的循环作用是导致铁路路基发生翻浆冒泥的主要因素[16-20]。部分学者考虑测试时间成本过高的影响，在以往研究的基础上，提出操作简单且能有效计算铁路路基是否发生翻浆冒泥病害的经验公式，基于该方法分析列车运行速度、轴重以及土的固结系数等参数对铁路路基翻浆冒泥的影响[21]。但事实上，由于现场环境复杂多样、车速及轮轴荷载变化等原因，通常会导致路基土的强度和轨道结构传递给路基的动应力表现出一定的变异性[22]。上述研究多是单一的考虑路基土在固定列车荷载作用下土体内部力学响应特征，分析时鲜有考虑参数不确定性影响，致使结果不够准确，故在讨论翻浆冒泥影响因素的基础上应进行不确定分析。采用敏感性分析和可靠度分析的方法可较好地解决不确定性问题，且可从概率的角度分析普铁路基发生翻浆冒泥的可能性。

本文基于王威等[21]提出的铁路路基翻浆冒泥计算模型，采用单因素法和极差法分析普铁列车轴重、车速、土的固结系数、固结应力比及围压在一定维修计划周期内对路基翻浆冒泥的影响，以此确定各参数的敏感度排序，从而选取敏感性强的参数作为基本随机变量，构建铁路路基翻浆冒泥病害发生的极限状态方程，用于评估参数不确定条件下路基的可靠性，进而评判其发生翻浆冒泥的风险。研究成果可为今后相关工程提供一定的借鉴。

1 铁路路基翻浆冒泥计算模型

大量有关铁路路基病害的研究及现场调查结果表明，路基若同时具备土层内含水量过高、土的塑性指数及细颗粒含量过大、渗透系数过小等条件，则在列车循环荷载作用下极易产生翻浆冒泥，该病害的存在会对列车运行产生极大的安全隐患。为揭示铁路路基翻浆冒泥发生机理，王威等[21]总结几类易发生翻浆冒泥的路基模型，建立可有效描述路基土中振动孔压增长与消散规律的控制方程，并以此计算列车荷载下不同土层深度处的振动孔压比，用于判断该处路基土体是否会产生翻浆冒泥，具体表达式为

( 1 )

s.t.

( 2 )

σd|z=0=0.26P(1+αv)

( 3 )

( 4 )

( 5 )

式中：K为土体振动孔压比(反映翻浆冒泥的指标，一般认为K不小于1时，路基发生了翻浆冒泥病害)；η为关系系数；f为荷载振动频率；kc为土的固结应力比；n为正整数；γ为计算系数；H为土层厚度；Cv为土的固结系数；z为土层深度；σd为土体中任意位置的动应力；σc为路基土围压；a、b为经验常数，a=-0.2，b=1.3；m为破坏振次；P为列车轴重；α为速度影响系数，对于行车速度小于160 km/h的普速铁路，α=0.005[23]；v为行车速度；N为路基土体所承受的列车荷载振次；t为振动时间。

2 铁路路基翻浆冒泥的参数敏感性分析

一般情况下，线路的养护维修周期大都是按列车累积通过次数或路基使用年限进行安排。因此，由式( 1 )不难发现，在一定维修周期内(即假设线路承受某固定振次的列车荷载作用)，列车轴重P、行车速度v、土的固结系数Cv、固结应力比kc及围压σc均会对路基土中孔压比的增长产生影响。通常不同参数对分析结果的影响程度并不一致，采用敏感性分析法从众多参数中有效筛选出对结果有重要影响的参数，以便根据各参数的敏感度排序，制定相应的预防措施[24-25]。为方便比较上述5个参数对铁路路基翻浆冒泥影响程度的大小，在计算中可选取确定的列车荷载振次，并在路基最易发生翻浆冒泥的位置(通常距路基表面以下约0.6 m[26-27])，采用单因素分析法和极差分析法进行敏感性比较。

2.1 单因素分析法

根据单因素分析法的原理，可将土中振动孔压比K视为诸因素Xi的函数，表达式为

K=f(X1,X2,…,Xr,…,Xn)

( 6 )

利用影响因素Xr引起的土体振动孔压比相对变化率与该因素自身相对变化率进行比值的方式来衡量其敏感度，即第r个影响因素的敏感度Er为

( 7 )

式中：|ΔKr/Kr|为土体振动孔压比Kr相对变化率；|ΔXr/Xr|为因素Xr的相对变化率。

根据影响因素的类型，可将其分为：外部参数(列车轴重P、行车速度v)和内部参数(土的固结系数Cv、固结应力比kc、围压σc)。按式( 7 )进行敏感度计算，结果见表1。

表1 单因素分析结果

由表1可知，在外部影响参数中，列车轴重P的敏感度远大于行车速度v；在内部土体参数中，围压σc的敏感度最大，固结系数Cv及固结应力比kc两者的敏感度相当。

2.2 极差分析法

通过引入正交试验设计法[28]，基于统计学原理，利用极差法对结果进行分析，确定各影响因素的敏感性排序，并与单因素分析法所得结论作对比，验证其排序结果的正确性。

依据正交试验设计法原理，确定试验相关因素和水平，选取合适的正交表对不同试验方案进行计算。设定5个影响因素各有3种水平，共做18次试验，正交表可表示为L18(35)。因素水平、正交设计方案及计算结果分别见表2、表3，其中表2所列数据为参考以往研究及实践经验。

表2 因素水平

表3 正交设计方案及计算结果

基于表3的计算结果，采用极差分析法对各影响因素进行敏感性排序。极差分析法具体步骤为：①对各因素不同水平上试验值的平均数求极差；②依据各因子中极差值与影响程度成正比的原理，判定各因素的主次关系。针对L18(35)所安排的设计方案，通常记第j列因素S水平的计算结果之和为KSj，其极差Rj的解析式为

( 8 )

各因素的极差分析结果见表4。

表4 极差分析结果

由表4可知，列车轴重对土体振动孔压比增长的影响最显著，路基土围压与行车速度的敏感度次之，土的固结应力比及固结系数的敏感度相对较小，敏感性排序从大到小依次为：列车轴重、土体围压、车速、土体固结应力比、土体固结系数。其排序与单因素分析结果一致。由此可知，外部参数对铁路路基翻浆冒泥的影响较内部土体强度参数更为显著。但在实际工程中，由于现场环境复杂多样、车速变化以及轮轴荷载变化等原因，上述5个计算参数往往具有一定的变异性，在很大程度上会影响路基的服役性。因此有必要利用可靠度的相关理论，考虑各影响因素的不确定性，从概率的角度分析路基发生翻浆冒泥的可能。

3 铁路路基翻浆冒泥的不确定性分析

3.1 铁路路基翻浆冒泥发生的极限状态方程

通常情况下，当路基土中振动孔压比不小于1时，表明土体发生液化破坏，此时认为路基出现翻浆冒泥病害[29-31]，故本文将土体振动孔压比视为翻浆冒泥病害指标。因此，铁路路基翻浆冒泥发生的极限状态方程可表示为

Z=1-K=

( 9 )

根据可靠度理论[32]，失效概率pf和可靠度指标β分别为

(10)

β=1-Φ-1(pf)

(11)

式中：Φ(·)为标准正态累积分布函数。

本文是基于Monte-Carlo法运用自编的Matlab程序对翻浆冒泥病害指标的概率分布、失效概率pf及可靠度指标β进行计算。主要步骤为：①设定样本容量；②根据各随机变量的分布函数对其进行随机抽样，并将抽样样本分别代入式( 1 )、式( 9 )得到该指标各区间的样本及失效样本；③得到相对应的概率分布、失效概率pf及可靠度指标β。

3.2 计算参数的变异系数

事实上，由于土体的矿物构成、沉积条件、风化等作用以及列车在运行过程中人为干扰因素的影响，列车轴重P、行车速度v及路基土围压σc、固结系数Cv和固结应力比kc的变异性总是客观存在，它们并不是一个确定值，而是具有一定的随机性，在计算分析时需考虑这些参数的变异性。此外，考虑到内部三项土体参数彼此相互影响，故采用可反映路基土整体力学特性的土体强度参数S来表示。同时，由相关研究得出：列车轴重P的变异系数大约为0.1～ 0.2[32]；运行速度v的变异系数大约为0.05～ 0.15[33]；土体强度参数S的变异系数大约为0.1～ 0.3[34]。此时，假定计算参数P、v、S均服从正态分布，取3种变异程度(δ(1)、δ(2)、δ(3))进行分析，其变异系数见表5。

表5 计算参数的变异系数

3.3 普铁路基翻浆冒泥病害指标的概率分布

以表2中的水平2为例，当线路在一定的列车荷载振次条件下，根据式( 1 )采用定值法计算可得路基中最易发生翻浆冒泥位置处的翻浆冒泥病害指标(即为土体振动孔压比)为0.394 5，满足不超过1的标准，可认为路基并未出现翻浆冒泥，处于安全状态。随后引入列车轴重、车速及土体强度参数的变异性，对表5中的3种变异程度，依据其概率分布随机生成50个样本组合进行计算，分别采用正态分布、对数正态分布、Gamma分布3种随机分布类型对样本数据进行拟合。图1～图3分别给出计算参数在变异程度为δ(1)、δ(2)、δ(3)下引起翻浆冒泥病害指标直方图及3种概率密度函数拟合结果，并对最优分布进行拟合度检验。

图1 变异程度δ(1)下翻浆冒泥病害指标概率分布拟合

图2 变异程度δ(2)下翻浆冒泥病害指标概率分布拟合

图3 变异程度δ(3)下翻浆冒泥病害指标概率分布拟合

由图1～图3可知，在考虑计算参数变异性后，列车荷载作用下翻浆冒泥病害指标不再是一个定值，而是在一定范围内发生随机变化；且在3种变异程度下，各自引起的翻浆冒泥病害指标直方图均与对数正态分布曲线吻合良好，可认为近似服从对数正态分布。由此说明，利用概率分析的方法能从多角度反映列车荷载作用下路基土层内翻浆冒泥病害指标的不确定性，使得计算结果更接近工程实际。

为直观地对比不同变异程度对计算结果的影响，图4、图5分别给出翻浆冒泥病害指标在δ(1)、δ(2)、δ(3)3种变异程度下最优分布(对数正态分布)的概率分布和累积概率分布。

图4 铁路路基翻浆冒泥病害指标的概率分布

图5 铁路路基翻浆冒泥病害指标的累积概率分布

由图4、图5可知，变异程度分别为δ(1)、δ(2)、δ(3)时，统计得到的翻浆冒泥病害指标均值依次约为0.38、0.37、0.35，与定值法计算结果较为接近。此外，随着参数变异性的增大，翻浆冒泥病害指标的离散性会随之增强，曲线的分布范围也会扩延，但与定值法计算结果接近的概率在减小，超过1的概率在增大。由此可知，计算参数的变异程度越大，普铁路基发生翻浆冒泥病害的可能性就越大。

3.4 可靠度指标对参数变异系数的敏感性分析

为比较列车轴重P、行车速度v和土体强度参数S的变异性对路基发生翻浆冒泥的影响，本节利用上述建立的可靠度指标来评估路基的可靠性，进而评判发生翻浆冒泥的风险。计算所用数据见表5，同时保持列车荷载振次固定，最终得出不同变异程度下各参数在距路基表面以下0.6 m位置处的可靠度指标随变异系数的变化曲线。需要说明的是，在对某一参数的变异系数进行敏感性分析时，其他参数的变异系数保持不变，结果见图6。

图6(a)～图6(c)分别表示可靠度指标随列车轴重P、行车速度v和土体强度参数S变异系数的变化曲线。由图6可知，随着计算参数变异性的增强，可靠度指标会随之减小。其中列车轴重P的变异性对可靠度指标的影响最为显著，当其变异系数由0.1增至0.2时，可靠度指标减小约37%～48%。行车速度v的变异性对可靠度指标的影响次之，当其变异系数由0.05增至0.15时，可靠度指标减小约20%～33%。而土体强度参数S的变异性对可靠度指标的影响最小，当其变异系数由0.1增至0.3时，可靠度指标减小15%～22%，与上文敏感性分析的结果相印证。由此可知，在铁路路基设计与运营过程中，应重视参数P、v及S的变异性对路基翻浆冒泥的影响。

图6 可靠度指标与各参数变异系数的关系

对比图6(a)、图6(b)和图6(c)可知，若目标可靠度指标[35]βT=2.5，当变异程度为δ(1)、δ(2)时，整体上基本符合β>βT；而当变异程度为δ(3)时，达不到目标可靠度的要求。经综合考量，可将变异程度δ(2)作为列车轴重P、行车速度v和土体强度参数S变异性的控制标准。

4 列车轴重、速度均值对可靠度指标的影响

大量工程实践证明，铁路投入运营后，路基土在水文、气候及列车动载长期作用等条件的影响下，其强度难免会发生改变，并且由于现场环境较为复杂及列车通行频率较大，路基土不能及时地进行换填，长期以往，会增大路基发生翻浆冒泥的概率。而铁路上通常是采取限制列车速度及载重的方式来预防翻浆冒泥病害。因此，有必要在列车荷载振次变化的情况下，探讨列车轴重和速度均值对路基翻浆冒泥病害发生可能性的影响。

为使分析更具对比性并尽量减少变异系数COV对分析结果的干扰，本节统一假设列车轴重P、行车速度v和土体强度参数S的变异程度为δ(2)以模拟各参数变异性较大情况，并在土体强度参数S均值不变的基础上，分别计算列车轴重P和行车速度v取不同均值时可靠度指标随振次的变化关系，进而评价列车轴重、车速对铁路路基翻浆冒泥发生可能性的影响。主要分为以下两种情况：①列车运行速度为100 km/h时，轴重P分别取16、20、24、28 t；②列车轴重为22 t时，行车速度分别取40、80、120、160 km/h。在两种情况及变异程度为δ(2)的条件下，可靠度指标随列车荷载振次的变化曲线见图7。

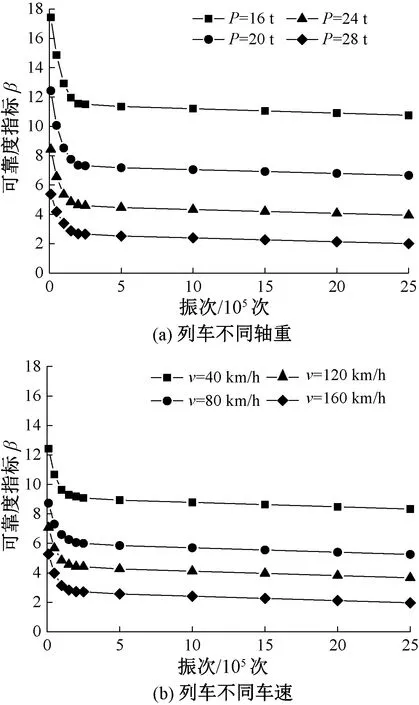
图7 外部参数不同下可靠度指标与振次的关系

由图7(a)可知，在相同振次下，随着列车轴重的逐渐增大，可靠度指标的变化量呈现出递减趋势，而在任一列车轴重下，可靠度指标均随着列车荷载振次稳定减小，在荷载加载前期可靠度指标迅速减小，而后减小的速度逐渐变缓；当列车轴重由16 t增加至28 t时，可靠度指标减小约69%～82%。由图7(b)可知，在相同振次下，可靠度指标的变化量并不随着车速的逐渐增加而呈现单调递减趋势，而在任一车速下，可靠度指标均随着列车荷载振次稳定减小，主要表现为在振次加载前期减小幅度较大，随后缓慢减小；当列车速度由40 km/h增至160 km/h时，可靠度指标减小约57%～77%。由此可知，增加列车轴重或行车速度，会显著影响到路基的服役性，继而越容易引发翻浆冒泥。

为尽可能延长普铁路基的检修周期并减小翻浆冒泥病害发生的可能性，依照3.4节目标可靠度βT=2.5的假定，由图7可知，应严格控制列车轴重和运行速度，避免因列车轴重过大或运行速度过快频繁引发翻浆冒泥病害，进而导致线路维修工作量加大、基床弹性骤降等不良现象。

综上所述，在实际工程中不仅需严格把控路基土的强度，更应详细调查运营线路中列车的轴重及速度信息。通过将敏感性分析与可靠度分析相结合，在确定各影响因素敏感性排序的基础上，综合考虑各因素变异性对路基翻浆冒泥的影响，分析结果不仅更为合理，且可采用目标可靠度为控制指标预防铁路路基病害的发生，更有利于达到提高路基服役性及优化列车运行环境的目的。

5 结论

本文基于铁路路基翻浆冒泥计算模型，采用单因素法和极差法分析普铁列车轴重、车速、土的固结系数、固结应力比及围压在一定维修计划周期内对路基翻浆冒泥的影响，进而选取敏感性强的参数作为基本随机变量，构建铁路路基翻浆冒泥病害发生的极限状态方程。随后利用正态分布、对数正态分布及Gamma分布3种随机分布类型对计算参数在不同变异程度下生成的样本数据直方图进行拟合，以此确定列车循环荷载作用下翻浆冒泥病害指标的最优概率分布类型并进行概率预测。进一步地，通过可靠度指标对计算参数变异系数的敏感性进行分析，讨论了列车荷载振次变化下不同列车轴重和车速大小对普铁路基可靠性的影响。现得出以下结论：

(1)单因素分析法和极差分析法取得了一致的敏感度排序结果，依次为：列车轴重>土体围压>车速>土体固结应力比>土体固结系数。

(2)考虑列车轴重、车速及土体强度参数的变异性后，翻浆冒泥病害指标表现出一定的离散性，且计算参数的变异程度越大，计算结果越离散；同时，3种随机分布类型的拟合结果显示，翻浆冒泥病害指标直方图均与对数正态分布曲线吻合良好，可认为近似服从对数正态分布。

(3)列车轴重和车速的变异性对路基翻浆冒泥影响非常显著，土体强度参数的变异性对路基翻浆冒泥具有一定的影响，故在实际工程中应严格控制列车轴重和车速，可有效减小普铁路基土发生翻浆冒泥的概率。

(4)在铁路路基前期施工及后期运营过程中，应高度重视路基的排水问题，确保路基土填料长期处于较干燥状态。