面向铁路定位装备测试的实时卫星信号生成方法

刘宇航，巴晓辉,2,3，蔡伯根,2,3，姜 维,2,3，王 剑,2,3

(1.北京交通大学 电子信息工程学院, 北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京市电磁兼容与卫星导航工程技术研究中心, 北京 100044)

随着卫星导航系统在世界范围内迅速发展，GPS、GLONASS、GALILEO、BDS及相应的卫星导航增强系统已经开始在多种交通运输系统中发挥作用，“‘十四五’铁路科技创新规划”中也提出推进北斗卫星导航技术与铁路技术装备、工程建造、运输服务等领域深度融合的目标。铁路建造方面，在路轨建设中通过卫星导航接收机测量线路、关键点的高精度位置坐标，辅助轨旁设备的安装，同时为列控轨道数字地图库提供了数据[1]。在桥梁建设中，利用导航接收机监测桥梁形变，实现全天候、高精度的动态监测，提升了施工建设的智能化水平[2]。铁路装备方面，通过在站内建立卫星导航差分基准站，实现差分定位功能，提高了列车站内定位精度。在区间内，结合现代卫星导航系统多模、多个信号发射频段的特点，利用卫星精密定位技术感知列车的位置、速度以替代依赖应答器、轨道电路进行定位校正的传统手段，降低了区间内应答器等轨旁设备的数量，减轻了设备维护的工作量[3-4]。在铁路运营方面，车站工作人员、设备维护人员的位置也可通过便携的小型接收机获得，通过实时监测当前线路的占用状况协调工作人员的位置，避免因调度问题而出现事故，最大限度保障列车及维护人员的安全[5]。应用卫星导航定位技术建立面向列车运行控制、维护维修、应急救援等业务方向的人、车、物定位网络是下一代列控系统建设的关键问题。

作为提供位置服务的终端设备，卫星导航接收机的稳定性和可靠性直接影响列控系统的运行安全，针对接收机的性能进行测试是贯穿列控系统研发使用周期的重要环节，生成针对不同场景的卫星模拟信号则是接收机性能测试的重要手段。在设备研发阶段，需要模拟列车在多种复杂场景下的运行情况验证列控系统的可靠性，如超长隧道、坡道、高速运行、制动等场景。通过软件信号模拟技术设计对应的场景，可以弥补场景数据的缺失，为接收机和列控系统的仿真测试提供平台。在列车运营阶段，我国西部地区铁路普遍面临着高寒、高海拔等恶劣的自然条件，车载设备损耗率高，需要定期在现场对车载设备进行检修，验证设备在不同场景下的定位能力。面向运营、维护、救援等人员的便携定位设备同样需要对定位性能进行测试，保障工作人员的安全。为此，一种依据所需场景自定义快速生成卫星模拟信号的方法对于新型列控系统的研发、维护具有非常重要的意义。

获取卫星模拟信号一般使用信号模拟器，传统的模拟器一般基于CPU+FPGA架构进行开发，新一代的硬件信号模拟器可以支持四大卫星导航系统以及QZSS、SBAS、IRNSS等星基增强系统的信号模拟，可实现上百个通道并行的高动态信号仿真[6]。但传统的卫星导航信号模拟器体型较大，不便于在现场对车载设备进行测试，并且价格昂贵，不适合大规模推广。而兼顾了便携性的小型化硬件模拟器，往往会面临性能不足的问题，工作时间和信号通道数量都无法达到要求。使用信号回放仪也可以产生卫星信号,但是信号回放设备只能播发已经采集的真实信号文件，无法根据场景设计可见卫星数量，载噪比等关键参数，不满足灵活设计测试场景的需求。

随着通信行业的技术发展，软件定义无线电(Software Defined Radio，SDR)技术以其灵活性高，研发周期短等优点逐步发挥着越来越重要的作用。在基带信号处理方面，大量学者基于软件无线电的思想研究了新型的卫星信号模拟算法[7]，但通常在高采样率下因计算量过大而出现信号生成过程实时性差的缺点[8]。近年来图形处理器(Graphic Process Unit, GPU)的发展为软件无线电的研究提供了新的解决方案，主流的GPU可以集成在大众消费级别的PC机上，并且其对大规模并行数据处理的加速能力已经在机器学习、深度学习等领域得到应用。利用GPU并行计算的优点，使用CPU与GPU结合的异构计算方式可以解决无法实时生成信号的问题。相比于传统的卫星信号模拟器，基于GPU生成模拟信号的方法具有场景灵活度高、实时性好、便于算法验证等优点[9]；并且可模拟信号通道的数量仅与芯片算力相关，不需要额外增加电路，结构灵活[10]，可以在普通的PC机上运行，设备成本低，体积小，便于携带和推广。

针对基于GPU生成卫星信号的算法已经进行过一些研究，文献[11-12]针对GNSS信号设计了并行算法，将中频数据中采样点的生成分配到各个线程之中，实现了多通道高采样率卫星信号的实时生成，文献[13]对GPU的内存模型进行了改进，通过重复调用寄存器存储来减少对共享内存的使用，提高了程序运行效率，并实时生成了BDS B1信号和BDS RDSS信号。文献[14]使用两块高性能GPU实现了对GNSS频谱的全覆盖。以上研究充分体现了GPU在信号模拟器方面的巨大潜力，但对于软件信号生成方法来说，由于计算机位长有限导致数值有效数字位数固定，在对相位进行累加时，超出有效数字外的部分会因累加引入误差影响信号的准确性。此处改进了相位累加计算过程，详细分析了基于GPU的并行计算模型并推导了在信号生成过程中典型参数的计算方式。依据真实线路数据设计了测试案例，验证了软件信号生成方法在定位装备测试方向的实用性和可靠性。

1 卫星信号数学模型

GNSS信号模拟源产生的信号为接收机内部经过射频前端下变频、采样后的中频信号。在编写信号模拟算法时，可以通过对接收机中频信号公式离散化计算采样点的具体数值。以GPS L1C/A为例，在信号射频发射端信号构成为

( 1 )

在信号传播过程中，到达接收机端的信号受到对流层、电离层、多径效应等影响。精确计算射频信号的传播时间不仅需要考虑卫星与接收机之间的距离、卫星自身时钟误差，还需要补偿传播路径中的误差。

首先，计算卫星和接收机之间的实际距离带来的信号传播时间，需要获得发射时刻的卫星位置和接收时刻的接收机位置。由星历解算得到的卫星位置和接收机位置都表示在ECEF坐标系下，随着地球自转，这两个时刻ECEF坐标系在空间中的位置已经发生变化。需要将发射时刻卫星位置的ECEF坐标旋转到接收时刻的ECEF坐标系进行计算。采用迭代的方法获得高精度的传播时间，依据星历推算接收时刻卫星和接收机之间的距离，获得信号传播时间初值，在此基础上对传播时间T′P按照以下步骤进行迭代：

Step1通过信号传播时间得到信号发射时间，依据卫星轨道参数推算卫星在发射时刻位置。

Step2将Step1得到的位置按照式( 2 )旋转到接收时刻的ECEF坐标系中。

式中：PR为在接收时刻ECEF坐标系下的坐标；PT为发射时刻卫星位置的ECEF坐标；Ωe为地球自转角速度。

Step3计算卫星与接收机之间的距离，得到新的信号传播时间。若两次传播时间相差小于阈值则认为当前传播时间为准确值，否则进行Step2。

根据Klobuchar模型，使用导航电文中包含的8个电离层参数计算电离层延迟误差△ρiono，但是若直接设置电离层延迟误差为diono=△ρiono，对于接收机将不存在电离层误差影响，因此需要调整电离层误差模型，该模型可消除60%左右的电离层误差，将电离层误差设置为diono=△ρiono/0.6[15]。

对于对流层误差dtrop，因为导航电文中不包含关于气象信息的内容，所以依据简化Hopfield模型进行处理

( 3 )

式中：θ为卫星仰角。

对于钟差Δtclk，计算式如下

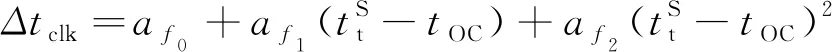
( 4 )

将信号经过对流层带来的距离误差折算到传播时间上，与卫星钟差一并计入信号传播时间。而电离层对载波相位有加速作用，对码相位有延迟作用，所以由电离层误差带来的传播时延单独列出，由此可以得到接收机射频端的信号为

( 5 )

射频信号经过下变频、滤波，频谱被搬移到基带，此时中频信号SIF(t)变为

( 6 )

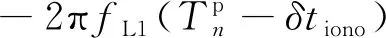
式( 6 )得到的中频数字信号模型建立了信号传播时间与载波相位、码相位和电文比特之间的关系。计算每一个采样点的信号传播时间和信号发射时间就可以得到采样点的具体数值。

2 基于GPU的模拟器工作原理

在中频信号的生成过程中，每一个采样点的生成方式都是依据式( 6 )调制得到，具有重复性。对于每一个采样点而言，调制方式并不复杂，符合GPU运算单指令多数据流(Single Instruction Multiple Data, SIMD)的规则，可以采用适当的并行结构加速软件信号生成过程。

2.1 信号生成软件架构

信号生成软件使用CPU与GPU异构并行计算的结构，软件工作逻辑见图1。中频信号采样点由信号功率、伪随机码、载波、导航电文四部分组成，其中，CPU主要计算信道模型的参数，获取载波相位、码相位和导航电文的初始值。GPU负责将CPU计算得到的参数带入到公式中，得到每一个中频信号采样点的值并将得到的数据拷贝到主机内存中。

图1 信号生成软件工作逻辑

2.2 并行计算模型设计

在CPU与GPU异构计算架构中，将CPU及主机中包含的存储空间称为主机内存，将GPU包含的存储空间称为设备内存。受限于设备内存的大小，不可能一次性在GPU中生成所有的中频数据，所以对数据进行分块是必要的。在式( 6 )中，每一个采样点对应一个信号传播时间Tp，但在每个采样点都计算一次信号传播时间所需计算量过大，同时考虑到信号传播时间在较短的时间间隔内变化不大，设时间间隔为△t，可以认为在△t内信号传播时间是不变的，并以△t作为中频数据的分块依据，调用一次核函数生成的信号时长为△t。

多普勒频移可以通过两次相邻的信号传播时间计算得到

( 7 )

式中:Rn为第n次得到的伪距；fd为多普勒频移；△t为接收机轨迹采样点之间的时间间隔；λL1为GPS L1C/A码信号的波长。

导航电文可以通过RINEX (Receiver INdependent EXchange format)文件中包含的轨道参数和电离层等数据逆向求解得到，也可以直接使用接收机解调得到的导航电文。每颗卫星的伪随机码序列提前通过移位寄存器生成，与导航电文共同保存在设备内存之中。

码相位和载波相位的计算通过数控振荡器的形式来实现，每次步进的长度由多普勒频移计算得到，以串行的方式计算中频信号采样点数值时，每个点的载波相位和码相位都可以通过上一个采样点与步进值累加得到，但是在GPU中每个采样点都是并行生成，无法依据上一个采样点进行推导。通过分析GPU的线程组织结构[17]可知(图2)，所有线程自上到下可以分为Grid、Block和Thread三级，每一级都有独立的编号，并且该编号是按照顺序排列的，可以利用编号定位到某一具体线程，相当于每个线程都有一个独立的ID。

图2 GPU线程组织结构

在以上对多普勒频移的计算中，可认为在△t内多普勒频移是不变的，所以在同一时间间隔内的所有采样点都有相同的码相位步进和载波相位步进，可以通过每个线程的ID与相位步进相乘得到这个采样间隔内所有采样点的码片相位和载波相位。

依据线程ID与相位步进的关系，可以得到图3所示的并行线程模型。

图3 GPU并行线程模型

在计算采样点的过程中，由于采样频率一般为几十兆赫兹，采样点数量K远大于可见卫星数量N，所以将并行计算模型设计为二维的Block和一维的Grid相组合的结构。在Block中，每一行代表对应的可见卫星，每一列代表中频信号在该时刻的采样点，由于Block内对线程数量的限制，在一个采样间隔内的采样点需要M个Block来计算

M×K≥samples

( 8 )

式中：samples为一个时间间隔内所有采样点数量。

由此可以得到每个采样点的载波相位carrphase和码相位codephase分别为

( 9 )

依据公式( 6 )，利用CPU提前计算载波相位初值、码相位初值、导航电文及信号功率，可以在GPU每一个线程中生成一个采样点，生成中频信号的公式可以改写为

(10)

式中：N、M、K分别为通道数量、Block数量、一个Block中包含的采样点数量。

在软件实现的过程中，受限于计算机字长，使用双精度浮点数计算相位步进位的有效数字为15～16位，同时中频信号采样率一般在107～108Hz之间，如果不对相位进行修正，相位偏差必然会随着采样时间增长而加大。事实上，累加得到的相位和每个△t时刻计算的初始相位是同一个值，可以利用这一点对相位进行校正。下面对这一点进行证明，码相位初始值由信号发射时间得到

(11)

式中：[x]表示对x向0取整。

信号发射时间可以表示为

(12)

同理可得，以一个时间间隔之后的时刻作为信号起始时间所对应的发射时间

(13)

两式相减可以得到两次发射时间之间的时间间隔

Δtt=Δtr-(Rn+1-Rn)/c

(14)

由此可得到两次接收时刻之间相差的码相位ΔPcode为

ΔPcode=[Δtr-(Rn+1-Rn)/c]×fcode

(15)

在GPU中通过相位步进与线程编号相乘计算码相位，码相位步进codeNCO的计算式为

(16)

在一个时间间隔内，一共产生Δtr×fs个采样点，代表线程ID的最大值，在该线程得到的码相位为

[Δtr-(Rn+1-Rn)/c]×fcode

(17)

可以看出式(17)与式(15)得到的结果一致，这里对比了码相位增加的总和，实际使用时还需要与伪随机序列长度取模得到采样时刻对应的伪随机序列数值。

对于载波相位，由式( 6 )得到，接收信号在下变频到中频之后的载波相位初始值可以表示为

(18)

式中：λ为波长。

以经过一个时间间隔的时刻为初始时刻，得到的载波相位初值为

(19)

两式相减可以得到在两次接收时刻载波相位的差值

Δφ=fIF×Δtr-(Rn+1-Rn)/λ

(20)

在GPU中通过相位步进和线程的ID计算载波相位，载波相位步进的计算式为

(21)

将式( 7 )带入式(20)，在最后一个采样点所在线程得到的载波相位为

ΔPcarrier=carrierNCO×fs×Δtr=

fIF×Δtr-(Rn+1-Rn)/λ

(22)

可以看出式(22)与式(20)得到的结果是一致的。在每一个Δt时刻的相位值与依据初始相位在GPU线程内计算的相位值是相同的，使用双精度浮点值计算相位在一个时间间隔之内并不会对定位精度产生显著影响。在每一个Δt时刻进行相位校正也保证了相位之间不会产生跳变，接收机的跟踪过程可以连续进行。

2.3 GPU内存分配

在Nvidia GPU内部为不同的数据结构和内存读取方式定义了一些特殊的内存。如寄存器、共享内存、常量内存、纹理内存、全局内存、锁页内存等，合理划分内存资源可以提高程序并行效率。

在2.2节的并行计算模型之中，一个Block内部同时产生了多路卫星信号的采样点，而信号生成软件最终得到的信号是各个卫星的信号相加，将各个通道的数据存储在共享内存中以实现同一个Block内不同线程之间的数据交互。对于信号叠加的过程，可以使用规约的方法计算以快速释放线程束，增强并行效果。

导航电文和伪随机序列对于同一个时间间隔内的采样点来说是不变的，考虑到GPU与CPU之间进行内存读取所占用的时间，可以把它们当做固定的查询表存放在设备的纹理内存之中。纹理内存专门用于存储图片、表格等数据类型，可以不按照内存的线性结构，读取任意位置的数据，同时纹理内存中的数据将通过纹理缓存读取，速度优于全局内存。

对于生成非零中频信号，载波调制所需的正余弦函数，在硬件模拟器中一般使用查询表的方式得到，省去了正余弦函数进行计算的时间。在软件实现的过程也可以借鉴查表方式，将正余弦函数表存放在纹理内存中，在每次调用时依据相位读取对应数值。

在核函数的执行过程中，需要将核函数输出采样点所需要的内存空间提前输入到GPU设备中，在核函数执行完成之后再由GPU的内存复制到主机内存中。由于模拟器采样频率较高，采样点内存的读取也将花费大量的时间，所以使用页锁定内存存放采样点数据。页锁定内存是在主机内存中开辟一块供GPU存取数据的空间，具有更高的内存读取速度。同时页锁定内存可以用于CUDA Stream，实现数据处理与传输层面的并行，掩盖数据传输延迟。

3 信号测试流程

信号测试流程见图4，首先选择用户轨迹并设计场景参数，输入到信号生成软件之中，之后利用CPU推算各颗卫星信号的初始参数，并将这些参数传入GPU设备内存中，利用并行计算模型同时计算每个通道内的信号采样值存入设备内存，最后将设备内存中的数据复制到主机内存中，供外部射频设备读取。

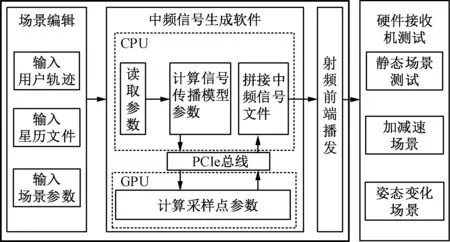
图4 信号测试流程

在场景编辑阶段，首先读取RINEX文件和用户轨迹，计算用户位置采样时刻的卫星位置，粗略计算伪距和卫星仰角，之后读取场景编辑参数，包括信号发射起始时间、卫星截止仰角、最大可见卫星数量和信号载噪比。比对发射起始时间和TOC时间判断是否更换星历，依据最大可见卫星数量和卫星截止仰角判断当前通道数量，设置载噪比控制信号接收功率。

在CPU处理阶段，将RINEX文件中浮点数形式的星历参数转换为二进制文件填充至导航电文各子帧对应位置，依据信号传播过程模型计算各颗卫星的伪距、传播时间、相位初值和多普勒频移。

在GPU处理阶段，将信号初始参数分配到并行模型中，在每一个线程中依据式( 6 )，结合线程ID计算采样点的数值，并将数值存入页锁定内存中。在生成一个Δt(用户轨迹采样点时间间隔)内所有通道的数字信号之后将数据传输到主机内存中，重复上述过程直至信号生成结束。

将主机内存中的数字信号数据复制到数据回放仪中，测试硬件接收机的定位效果。

4 实验验证及数据分析

4.1 实验设备及环境

生成模拟导航信号所使用的GPU型号为Nvidia Quadro T1000，使用的信号回放设备为Labsat3W,测试接收机的型号为ubloxM8U，用户轨迹文件数据来源分别为2018年6月京沈客运专线，2021年6月国家铁路实验中心环形实验场现场测量的轨道坐标数据，使用设备为高精度组合导航接收机SPAN(Synchronized Position Attitude & Navigation)。在数据中截取了静止、加减速状态、弯道状态三个场景。在三个场景中生成的中频数据，使用Labsat3W信号回放仪进行回放，中频信号的采样频率为58 MHz，并与ubloxM8U接收机连接测试定位效果。

4.2 信号生成算法实时性能分析

信号生成算法的运行时间主要与GPU线程模型的设计和本地时间间隔△t有关。

分析线程模型设计方面对实时性的影响需要考虑软件算法与GPU硬件结构的匹配，GPU通过将线程打包为线程束的形式分配给流多处理器(Streaming Multiprocessor, SM)来实现并行计算，在每个SM中线程束的占用率越高则说明当前程序的并行性越好。GPU中的硬件资源是有限的，随着线程数量的变化，每个线程可以使用的硬件资源也不同，这是影响线程束占用率的主要因素。实验所使用的GPU包含14个SM流多处理器，896个CUDA核心。

在2.1节分析的并行运算模型中，每个Block被设计为二维的线程结构，其中卫星信号通道这一维度是依据RINEX文件设定的，可以通过改变采样点数量K来寻找并行线程数量和每个线程可用资源之间的平衡。以58 MHz采样率,本地时间间隔100 ms，生成1 s信号为例，分别将采样点数量K设置为(8,16,32,64,80,96)，记录信号生成所用最短时间。这里K设置的最大值受限于每个Block最多可以容纳的线程数量和共享内存的总容量。设置不同的通道数量对应的生成时间如表1所示。

表1 不同通道数量生成数据时间

可见卫星数量satnum与一个Block中采样点数量K的关系见图5。从图5中可以看出，所有数字基带信号生成速度均快于实时，同时，并行效率最高的采样点数量K与通道数量存在反比关系，在实际应用中也可以通过通道数量动态调整每个Block中的采样点数量，达到最优的并行效果。本实验中，在通道数量为9的情况下并行效率最高的采样点个数为16，使用NVIDIA Nsight Compute工具分析该核函数运行效率如表2所示，其中内核使用率和线程占用率都达到较高水平。

图5 Block中采样点数量与时间关系

表2 信号测试实验设备型号 %

影响信号生成算法时间的另一因素为本地时间间隔△t。通常情况下，用户轨迹的抽样间隔是稀疏的，可以使用插值的方法增加用户轨迹点数，降低本地时间间隔，缩短参数更新周期。但是缩短时间间隔必然会增加计算量，同时由于计算信号传播时间等任务均在CPU中计算并传递至GPU，在缩短时间间隔后，GPU与CPU之间的数据传输次数也会随之增加，信号生成时间也会相应延长。为测试信号生成的实时性与本地时间间隔△t的关系，设置一组时间间隔分别为(1、2、5、10、20、50、100、150、200 ms)，在58 MHz采样率，9个信号通道，每个Block的采样点数量为16的场景下测试生成2 s信号所需要的时间，测试结果见图6。由图6可以看出,在58 MHz采样率并确保实时性的情况下，本地时间间隔可以达到5 ms。在信号生成过程中，可以针对不同轨迹的动态情况，设置不同时间间隔，确保实时性。

图6 本地时间间隔与时间关系

最终生成中频信号的频谱图见图7。

图7 中频信号频谱图

4.3 中频信号静态定位实验

产生静态场景，在ECEF坐标系中选择一静态点，坐标为(-2 184 063.256,4 378 949.513,4 077 218.686),使用ubloxM8U接收机对设备进行测试。表3为将实验结果转换到ENU坐标系的位置坐标，接收机解算结果静态平均位置和真实位置见图8。

表3 静态定位结果三轴误差 m

图8 静态定位结果

4.4 轨道测量数据定位实验

实验一：京沈客运专线轨道数据实验

为验证在动态场景下中频信号的稳定性和可靠性，选取2018年7月京沈客运专线黑山北站—沈阳西站区间实测数据中一段包含加减速的轨迹，线路总长度约为20 km。列车起始速度为247 km/h，经过两段减速后在259 s时进站停车，在339 s后开车，经三段加速过程后速度达到248 km/h。生成信号过程中，可见卫星数量为9颗，设置采样率为58 MHz，依据轨迹生成了620 s卫星信号，在并行参数设置方面，依据5.2节实时性分析，设置GPU线程中采样点数量K为16，用户轨迹时间间隔为100 ms，与传统的利用CPU方法对比，两种方法生成信号时间如表4所示。接收机的参考位置、速度通过列车上搭载的组合导航接收机SPAN得到，由参考位置作为用户轨迹生成模拟的卫星信号，再使用通用接收机得到解算位置，其中，经、纬、高三轴位置和速度见图9、图10。在接收单GPS卫星信号的情况下ubloxM8U接收机的水平位置误差为2.5 m，高程误差为3 m，速度误差为0.05 m/s[18]。位置、速度误差均值及方差如表5所示。由表5可以看出，列车的位置误差和速度误差都在接收机误差范围内。卫星信号生成方法在实时性和精度方面都满足测试要求。

表4 信号生成时间对比 s

图9 直线加减速场景定位结果

图10 直线加减速场景定位结果

表5 动态场景定位结果

实验二：国家铁路实验中心环形实验场轨道数据实验

为验证生成信号在弯道状态下的稳定性和可靠性，选取2021年6月在北京环形铁路试验中心的测试数据，该轨迹的圆环半径为600 m。信号生成过程中，由环形道轨迹生成了470 s卫星信号，由于该场景下可见卫星数量与实验一相同，所以并行模型参数的设置保持不变，实际位置和解算位置的获取方法与动态场景下一致。表6为两种方法信号生成时间对比，表7为环形道场景的定位误差，图11为平面定位结果，图12为经、纬、高三轴位置与实际位置比较结果，定位ubloxM8U接收机定位误差范围之内，由环形道轨迹生成的卫星模拟信号可以在弯道弧度较大情况下满足定位测试要求。

表6 信号生成时间对比 s

表7 环形道场景定位结果

图11 环形道场景平面定位结果

图12 环形道场景三轴定位误差

5 结论

卫星导航技术在列车运行、维护过程中的广泛应用对导航接收机的可靠性提出很高的要求，生成模拟的卫星信号是测试导航接收机性能的常用手段。针对传统的卫星导航信号模拟设备无法兼具场景设置灵活性和设备便携性的问题，引入一种基于软件无线电的思想，依托GPU与CPU异构并行计算架构的信号生成方法。详细分析了信号生成过程的并行计算结构，GPU内存结构以及场景参数设置方法。并将京沈高铁和北京环形铁道的实测轨道数据作为依据生成场景文件，分别设计了静态、加减速状态和弯道状态三个场景，实时生成卫星模拟信号，通过查阅技术手册获得所使用接收机的定位精度范围，得到的定位结果满足接收机定位精度，验证了生成信号的可用性。基于GPU的卫星信号生成方法能够快速生成卫星信号，并且能够依据场景设置参数，同时操作简单，满足卫星导航铁路应用中对接收机性能测试验证的需求。