轮轨界面低黏着对大功率电力机车车轮滚动接触疲劳的影响

刘永锋，赵旭峰，栗 杨，温泽峰，赵 鑫

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.株洲中车时代电气股份有限公司 轨道交通技术中心，湖南 株洲 412001)

和谐型大功率交流传动电力机车因具有功率大、速度快、运载能力强和节能环保等一系列优点而在我国大量服役，其在役数量已超过一万余台[1]。然而，在诸如大坡度坡道和小半径曲线等复杂线路运营时，和谐型大功率电力机车在踏面中部频繁发生如图1所示的滚动接触疲劳[2]。这些裂纹或仅在车轮踏面局部萌生(图1(a))，或沿车轮一周连续分布(图1(b))，但其萌生速率沿车轮一周并不均匀，这体现在镟修后发现仅有个别裂纹扩展较深(图1(c))。极端情况下，个别裂纹扩展深度可达14.5 mm[3-4]，即对应轮径镟除量高达29 mm，这严重威胁机车的安全运营。特别是考虑到一个车轮因疲劳裂纹镟修，其余健康车轮也因轮径差而须进行相应的镟修，这大幅缩短了轮对的使用寿命，极大增加了机车的运维成本。

图1 大功率电力机车车轮滚动接触疲劳

根据滚动接触疲劳裂纹萌生在车轮径向位置的不同，文献[5]将车轮滚动接触疲劳分为深层滚动接触疲劳(裂纹萌生在踏面下方10～25 mm)、次表面滚动接触疲劳(裂纹萌生在踏面以下3～10 mm)和表面滚动接触疲劳(裂纹萌生在踏面以下0～3 mm)，如图2所示。相对表面滚动接触疲劳而言，次表面和深层滚动接触疲劳的危害更大，且更不易被发现。但随着冶金工业水平的进步，车轮材质的力学性能和微观组织得到了显著改善和提升，使得这两类滚动接触疲劳近年来的发生率已明显降低[6]，而如图1所示的表面滚动接触疲劳则更为常见。

图2 车轮RCF沿径向和周向分类(单位：mm)

文献[7]根据表面滚动接触疲劳沿踏面横向的分布位置不同，将其分为4类，如图2所示，分别是名义滚动圆外侧的斜裂纹(RCF1)、轮缘根部的斜裂纹(RCF2)和踏面中部的横裂纹(RCF3)以及纵向裂纹(RCF4)。对于机车，RCF3的危害最大[3-4,7]，裂纹与车轴呈0°～10°夹角，其诱因被总结为过大的轮轨纵向蠕滑力[7]，典型的RCF3如图1所示。

车轮滚动接触疲劳的发展包括裂纹萌生和裂纹扩展两个阶段。根据车轮表面材料受载时的应力应变特性，文献[8]认为材料始终处于塑性安定或棘轮效应时，材料会因塑性和韧性耗尽而萌生裂纹。文献[9]根据车轮受载时的应力应变曲线是否闭合，进一步将材料的失效行为区分为低周疲劳失效(应变曲线闭合)和棘轮失效(应变曲线不闭合)，且这两种失效模式是独立和竞争的。

影响机车车轮表面裂纹萌生的因素较多，如不合格的增黏砂能在踏面引起麻坑损伤[10]，初始麻坑损伤可能发展成深裂纹[3]。机车同一轮对左右车轮过大的轮径差可加剧车轮的蠕滑，从而引起严重的RCF3[11]。踏面凹磨因在磨耗突变区减少了轮轨接触面积而导致接触应力增大，由此导致裂纹萌生[12]。国内机车的运维经验表明，JM3廓形的抗疲劳性能优于JM和JM2廓形[13]。

车轮表面较大的磨耗速率可将萌生的裂纹及时磨掉；但当低黏度流体进入裂纹时，可加剧裂纹的扩展速率[14-15]。相比裂纹扩展，裂纹的萌生里程更长[16]。因此，本文仅从裂纹萌生的角度开展分析。

滚动接触疲劳的数值研究通常借助于多体动力学[3-4]和有限元法[17-19]实现。有限元法能建立二维模型[17]或单个车轮[18]或单个轮对[19]的三维模型，其计算效率低，但可突破几何尺寸的限制。多体动力学能考虑整个列车的编组，如列车悬挂参数和线路参数等，且计算效率高，但轮轨接触求解存在诸多假设，且无法考虑裂纹的尺寸效应。因此，有限元更适合微观的机理研究。本文基于多体动力学仿真软件Simpack建立机车的多刚体动力学模型，结合滚动接触疲劳预测模型，从宏观的视角分析局部轨面低黏着(摩擦系数小于黏着需求)对车轮损伤的影响。

1 机车车轮滚动接触疲劳预测模型

1.1 多体动力学模型

作者在文献[3]中已建立了客运机车的多体动力学模型，其数值仿真结果与现场观测结果吻合较好，验证了模型的可靠性。该动力学模型由1节Co-Co轴式的机车牵引18节客车组成，机车轴重23 t，最高速度为120 km/h，机车的刚体模型包括1个车体、2个构架、6个电机、6个轮对和2个牵引杆；18节客车被简化为力元施加在机车车钩位置处，其总质量为1 008 t。模型考虑了机车和客车的基本阻力、曲线阻力和坡度阻力。

1.2 切向接触求解模型

由于RCF3位于踏面中部，其接触位置处的轮轨几何符合Hertz理论的假设，因此，法向求解采用Hertz接触理论。在机车车轮滚动接触疲劳预测中，轮轨切向接触求解多采用简化理论[11,20]和Polach模型[3-4,21]。

在文献[20]中，假设接触斑内每个质点的摩擦系数相同，但这与测试结果不符。试验发现，当轮轨相对滑动速度增大时轮轨摩擦系数会减小，即在较大的蠕滑率下轮轨之间的黏着能力会下降，而不是维持在库伦摩擦极限，如图3所示。

图3 干态和湿态轨面下典型的蠕滑力-蠕滑率曲线

为了考虑轮轨之间大蠕滑对轮轨表面摩擦系数的影响，文献[21]引入了与蠕滑率相关的摩擦系数

μ=μ0[(1-λ)e-Bω+A]

( 1 )

式中：μ为摩擦系数；μ0为最大摩擦系数；B为摩擦系数指数衰减系数；ω为轮轨之间的相对滑动速度；A为滑动速度为无穷大时对应的极限摩擦系数与最大摩擦系数之比。

文献[21]给出了轨面干态和湿态下的典型输入参数，见表1。

表1 Polach在干态和湿态下的典型输入参数

为了对比简化理论和Polach模型在考虑机车牵引/制动时的差异，以文献[3]中建立的机车多体动力学模型为例，对比其沿直线下坡轨道匀速运行时的轮轨纵向蠕滑率。设置坡度i=-12‰、-24‰时(负号表示下坡)，对应的机车速度分别为90、50 km/h，仅采用机车的电制力制动，轨道不平顺采用美国五级谱。考虑到施加的电制扭矩相同，两种切向求解模型下车轮的纵向蠕滑力基本一致，因此，仅给出了纵向蠕滑率的对比结果，如图4所示。

图4 简化理论和Polach模型计算的纵向蠕滑率对比

由图4可知，轨面干态下，当坡度i=-12‰时，两个算法求得的纵向蠕滑率基本一致；当坡度i=-24‰时，Polach模型下的纵向蠕滑率明显更大，其增幅大约为60%。轨面湿态下，两个算法的差异更为明显，与简化理论相比，Polach模型下的纵向蠕滑率更大，如i=-24‰时，其纵向蠕滑率相比简化理论约增大4倍。这是因为随着电制力增大，轮轨界面需要大的蠕滑率提供更高的黏着，显然，简化理论未考虑这一点。

根据文献[22-23]可知，蠕滑率对轮轨滚动接触疲劳具有明显的影响，特别是当蠕滑率大于0.3%时，车轮的寿命会明显降低。在文献[24-25]中，将蠕滑率作为轮轨表面是否萌生裂纹的关键阈值，换言之，蠕滑率对车轮表面裂纹萌生的影响不可忽略。因此，采用能考虑大蠕滑的Polach理论模型更为精确。

1.3 车轮滚动接触疲劳预测模型

两个适用于多体动力学的滚动接触疲劳预测模型分别是安定图[8]和损伤函数[26]。安定图基于全滑假设，无法考虑蠕滑率的影响，这与RCF3发生在踏面中部使其接触斑内通常发生的是局部滑移这一现象不符。因此，本文采用能考虑蠕滑率的损伤函数模型预测车轮的滚动接触疲劳，如图5所示。图5中横坐标表示磨耗数，其计算式为

Tγ=Fxγx+Fyγy

( 2 )

式中：Fx、Fy分别为车轮的纵向、横向蠕滑力；γx、γy分别为车轮的纵向、横向蠕滑率。

基于接触斑内的磨耗数以及4个关键参数见表2，计算车轮的总损伤，并通过磨耗与滚动接触疲劳损伤值的代数叠加考虑滚动接触疲劳与磨耗之间的竞争，并判断车轮踏面损伤是以磨耗为主还是以滚动接触疲劳为主。

图5 损伤函数

表2 损伤函数关键参数

损伤函数考虑了轮轨界面低黏度流体对裂纹萌生速率的影响。当纵向蠕滑力与速度方向相反时，接触斑内的裂纹被拉开，低黏度流体进入裂纹中促使裂纹生长；纵向蠕滑力方向与速度方向相同时，接触斑内的裂纹闭合，流体无法加速裂纹的生长。因此，本文仅分析机车电制下的工况。需要说明的是，车轮磨耗计算仅与磨耗数的大小有关，而与纵向蠕滑力的方向无关。

2 数值结果

在文献[3-4]中，设定的仿真工况均假定轮轨界面之间的最大摩擦系数始终保持不变。然而，真实运营环境中，钢轨表面不可避免地存在油污、雨水、霜雪和树叶等局部污染，从而在轨面产生局部低黏着。参考文献[27]设置轨面的局部低黏着如图6所示，低黏着区的轮轨摩擦系数分别设置为0.06、0.18，低黏着区的两端均设置0.5 m长的过渡区，过渡区外的轨面摩擦系数均设置为0.3，即对应表1中的湿态工况。

图6 钢轨表面局部低黏着设置

本文仅分析蠕滑控制系统不介入的局部低黏着区，这是因为：

(1)这类短低黏着区在运营中更为常见。

(2)根据文献[25-26]可知，当轮轨表面的蠕滑率大于0.01时，车轮的损伤由磨耗主导，而机车蠕滑控制的蠕滑率阈值远大于0.01[28]，即蠕滑控制系统介入前车轮的疲劳损伤可能更为严重。

2.1 仅单侧轨面有低黏着2.1.1 曲线轨道

根据文献[3-4]可知，机车以1轴导向通过如图7所示的右曲线时，仅图7中3轴和6轴车轮的接触点位于名义滚动圆区域。由于前后转向架对应车轮的损伤基本一致，因此，仅展示3轴车轮的损伤结果。以半径为600 m的右曲线下坡轨道(i=-14‰)为例，机车速度为70 km/h，电制力为112 kN，超高设置为95 mm。

图7 机车通过右曲线示意

(1)仅低轨侧轨面有低黏着

仅当曲线低轨侧轨面存在低黏着区时，3L和3R车轮的损伤结果如图8所示。图8中，横坐标表示车轮沿轨道纵向的滚动距离，纵坐标表示车轮的损伤峰值，即根据损伤函数计算出接触斑内的总损伤，按照半椭圆进行离散后求得接触斑内的最大损伤，其正值和负值分别表示滚动接触疲劳和磨耗。当同一位置的损伤峰值累积为1时，车轮接触斑内可萌生长度不小于10 mm的裂纹[26]。

图8 曲线段低轨侧存在低黏着区时的车轮损伤

由图8可见，3R车轮无损伤发生，而3L车轮的损伤由滚动接触疲劳主导，且摩擦系数越低，裂纹的萌生速率越大。以μ0=0.06为例，图9给出了通过低黏着时轮轨纵向蠕滑力的变化。可见，车轮的纵向蠕滑力由曲线和电制力两部分叠加组成，当μ0=0.3时，电制力在两车轮上引起的纵向蠕滑力均为-9 kN，而曲线在3L和3R车轮上引起的纵向蠕滑力分别为-6 kN和6 kN；叠加后3L车轮的纵向蠕滑力为-15 kN，即使得3L车轮的损伤由滚动接触疲劳主导，而3R车轮的纵向蠕滑力为-3 kN，使得其接触斑内的磨耗数过小而无损伤发生。

图9 低轨侧存在μ0=0.06的低黏着区时车轮的蠕滑力变化

当机车通过μ0=0.06的低黏着区时，由于低轨侧3R车轮的纵向蠕滑力幅值仅为3 kN，其对黏着的需求很小，因此，其纵向蠕滑力仅从3 kN降为2 kN。考虑到纵向蠕滑力对轮对的扭矩须与机车电机的输出扭矩保持平衡，因此，3R车轮纵向蠕滑力的减小必然导致3L车轮纵向蠕滑力的增加，即3L车轮的纵向蠕滑力由15 kN增加至16 kN，继而导致3L车轮的裂纹萌生速率增大。换言之，曲线段低轨侧存在低黏着区时，仅增大高轨侧车轮的裂纹萌生速率，且其随轨面摩擦系数的降低而增大。

(2)仅高轨侧轨面有低黏着

仅在曲线段高轨侧轨面设置局部低黏着区，其余仿真条件不变，3L和3R车轮的损伤结果如图10所示。可见，当车轮由湿态轨面驶入低黏着区轨面时，3L车轮的裂纹萌生速率降低。当μ0=0.18时，3R车轮无损伤发生；当μ0=0.06时，3R车轮由无损伤演变至裂纹萌生且萌生速率急剧增大。相应的轮轨纵向蠕滑力变化如图11所示，即当3L车轮进入μ0=0.06的低黏着区后，低轨侧3R车轮的纵向蠕滑力由3 kN增大至13 kN，导致3R车轮萌生RCF3。当轨面黏着恢复后，3L车轮的裂纹萌生速率增大，而3R车轮的裂纹萌生速率降低。

图10 曲线段高轨侧存在低黏着区时的车轮损伤

图11 高轨侧有μ0=0.06的低黏着区时车轮的蠕滑力变化

需要指出，μ0=0.18时，其3L车轮的裂纹萌生速率降低并未导致3R车轮的裂纹萌生速率增大，其原因是3L车轮的纵向蠕滑力的降幅较小。

2.1.2 直线轨道

当机车牵引18节客车在14‰直线下坡轨道运行时，设置速度为80 km/h，电制力为162 kN，参考图6，仅在左侧轨面设置局部低黏着区。直线轨道时各个车轮的接触点均位于名义滚动圆区域，其损伤也基本一致。因此，以导向轮对车轮1L和1R为例进行结果展示。当μ0=0.18、0.06时，1L和1R车轮的损伤如图12所示。

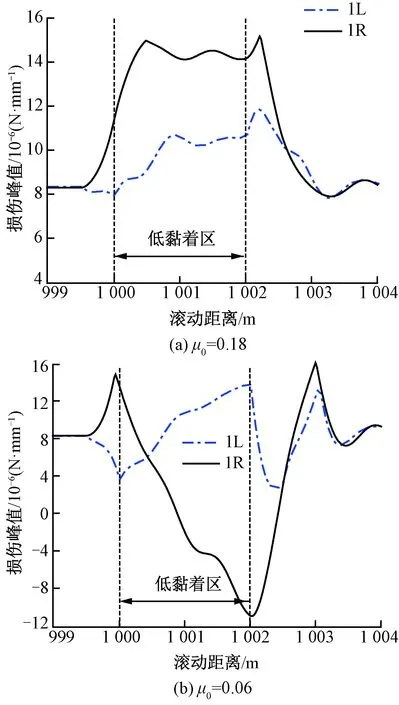
图12 左侧轨面有μ0=0.18、0.06的低黏着区时导向车轮的损伤

由图12(a)可见，当进入低黏着区后，1L车轮的裂纹萌生速率增大，但1R车轮的增幅更大。这表明，单侧轨面的局部低黏着区可导致两侧车轮的裂纹萌生速率增大，且非低黏着侧的车轮更严重。由图12(b)可见，当轨面摩擦系数进一步降低至0.06时，1R车轮的裂纹萌生速率达到最大后迅速降低，直至磨耗主导，这是磨耗与疲劳竞争的结果。

图13给出了μ0=0.06时车轮的纵向蠕滑率和纵向蠕滑力的演变。由图13可见，在低黏着区时，左右两侧车轮的纵向蠕滑率均增大，且其幅值基本一致。这是因为左右车轮的角速度相同且其接触点均位于名义滚动圆区域。在低黏着区内，1L车轮的纵向蠕滑力降低，而1R车轮相应的增加，这解释了图12车轮损伤结果。

图13 左轨面有μ0=0.06的低黏着区时车轮的纵向蠕滑率、蠕滑力

2.2 双侧轨面有低黏着

考虑设置双侧轨面均存在摩擦系数相等的低黏着区，不改变2.1.2节的其余仿真条件，以1L车轮为例，其损伤结果如图14所示。由图14可见，低黏着区内车轮的损伤峰值达到最大值后随低黏着区长度的增加而降低，车轮的损伤最终由磨耗主导。这是因为双侧轨面低黏着区内的摩擦系数降低会导致左右两侧车轮纵向蠕滑力同时减少，破坏了纵向蠕滑力与电机扭矩之间的平衡关系，导致轮对角速度降低而引起纵向蠕滑率增大。当纵向蠕滑率大于蠕滑特性曲线饱和黏着点对应的蠕滑率之后，蠕滑率的增大引起轮轨接触内的黏滑振动，反而进一步降低了轮轨界面的摩擦系数(见图3)，而摩擦系数的降低会进一步导致纵向蠕滑率增大，如此在纵向蠕滑率和轮轨摩擦系数之间产生一个相互反馈的恶性循环，直至车轮的蠕滑控制系统介入或轨面黏着条件改善。因此，当车轮的裂纹萌生速率达到最大后，会迅速在磨耗的竞争下下降。

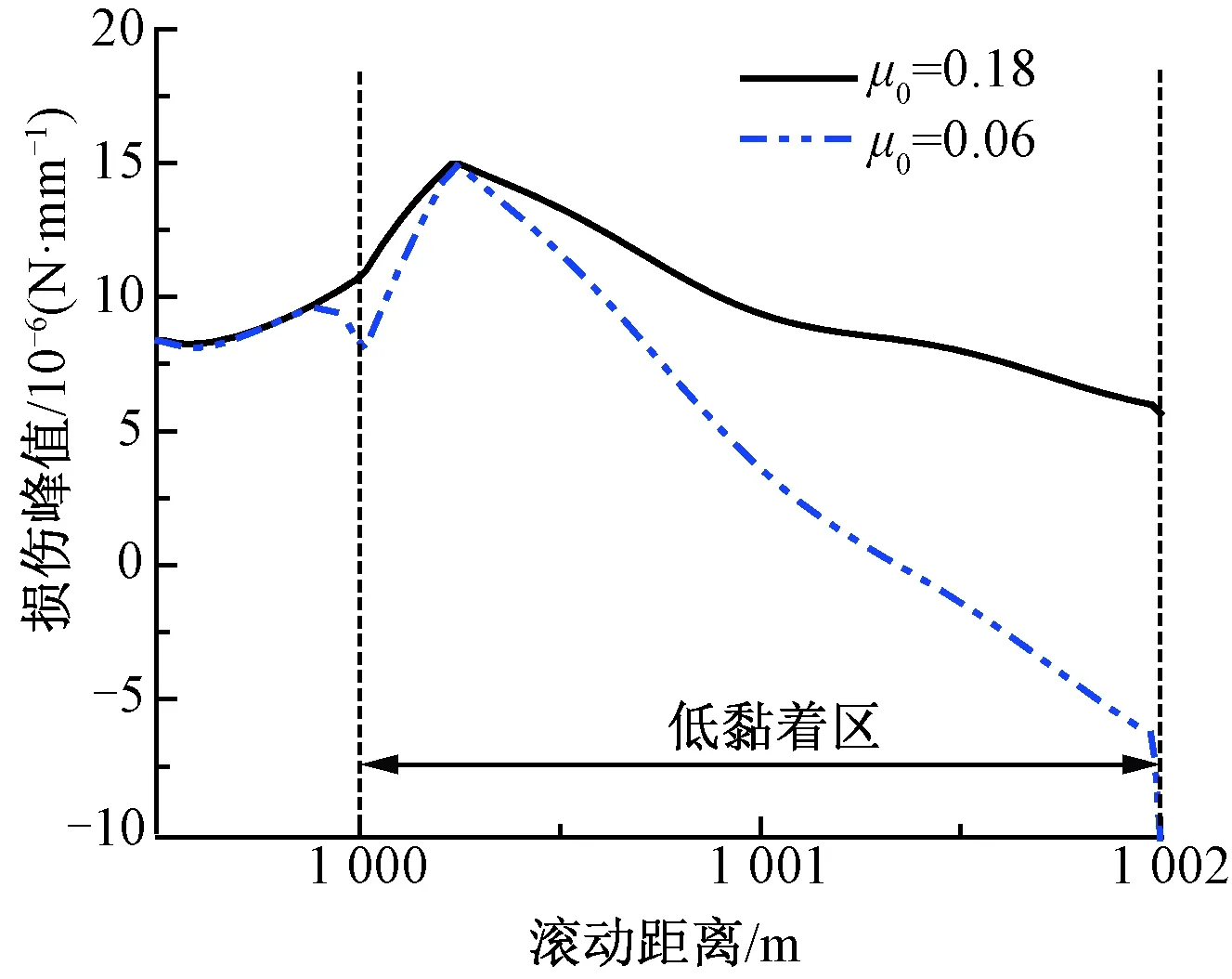
图14 直线轨道双侧轨面均有低黏着时车轮损伤

当机车车轮滚动圆处的直径为1.15～1.25 m时，车轮的周长约为3.611～3.925 m，当车轮在小于其周长的低黏着区运行时，会沿车轮周向萌生局部滚动接触疲劳或滚动接触疲劳裂纹的萌生速率沿车轮一周分布不均，即轨面局部低黏着区可引起图1所示的车轮局部滚动接触疲劳。需指出，滚动接触疲劳是一个长期损伤积累的过程，本文仅仿真了低黏着区段车轮滚动一小段距离内损伤峰值随距离的变化，但实际中每次低黏着发生时车轮的起始位置是随机的。这种随机性通过长期积累可能某种程度上会抵消仿真研究中存在的沿车轮一周的萌生速率的不均匀性。

3 结论

本文建立大功率电力机车多刚体动力学模型，结合损伤函数，探究轨面局部低黏着对车轮名义滚动圆附近发生的第三类滚动接触疲劳的影响，得出如下结论：

(1)机车在直线下坡电制运行且单侧轨面存在低黏着区时，低黏着区内两侧车轮的裂纹萌生速率均迅速增大，但非低黏着区侧车轮的裂纹萌生速率增幅更大。

(2)机车在曲线下坡电制运行时，仅当低轨存在低黏着区时，高轨车轮的裂纹萌生速率增大，仅高轨存在低黏着区时，高轨车轮的裂纹萌生速率降低，而低轨车轮的裂纹萌生速率增大。

(3)当机车在双侧轨面均存在低黏着区的直线下坡运行时，由于磨耗的竞争，裂纹的萌生速率随低黏着区长度的增加而先增大后减小。