基于小波变换的弓网接触压力特征研究

李三喜，张 坚，李 鑫，刘文正

(1.北京铁路电气化学校, 北京 102202；2.长江师范学院 机器人工程学院, 重庆 408100；3.中车青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266111；4.北京交通大学 电气工程学院, 北京 100044)

弓网受流质量一般是以弓网接触压力为评价指标，而接触压力受接触网结构的影响随着列车的前行而不断变化，即接触网结构参数的变化直接影响接触压力。当列车运行速度提高，受到轮轨振动、气流激扰等外部因素的影响，弓网间的振动加剧，导致弓网间的受流质量变差，弓网接触压力的变化规律更加复杂，甚至出现接触压力为零的离线现象。

国内外专家学者在改善弓网受流质量方面进行了广泛研究，并取得了很多成果。为了解决列车高速运行时弓网离线增多的问题，文献[1-3]分析了接触线挠度、刚度等与接触压力间的关系。文献[4-7]基于半实物仿真方法，在进一步完善弓网仿真系统的基础上，分析了接触网刚度、气动抬升力等对弓网接触压力的影响。文献[8-11]通过改变受电弓参数分析接触压力的变化规律。文献[12-13]为了判断接触线的不平顺问题，通过采用EEMD法、ZAMD法等对弓网接触压力进行时频变换来实现目标。上述研究对各影响因素对弓网接触压力及弓网动态特性的影响进行了比较全面的分析，但多是以接触压力平均值、标准偏差等统计参量为评价指标对某一区段内的接触压力变化进行的整体性分析。随着列车运行速度的提高，接触压力的周期分量及吊弦点处的突变值出现不同程度的变化，尤其是吊弦点的接触压力值突变加剧，严重影响弓网受流质量。因此，如何分解接触压力的周期信号以及提取吊弦点的突变量，成为亟待解决的关键问题。

为了分析列车高速运行时接触压力的周期分量，提取吊弦点的突变量，本文采用小离散小波变换法，提取接触压力的特征信号。小波变换是以傅里叶变换为基础的时频分析方法，该方法是用时间和频率的联合函数来表示信号，克服了传统傅里叶变换在全局变换方面的不足，而且能够进行多分辨率的信号分析，能够体现信号在时域和频域方面的局部细节特征[14]。

因此，本文基于有限元法，建立弓网仿真模型，得到不同条件下的接触压力；采用一维离散小波变换，将接触压力分解为5层，得到接触压力的周期信号分量和高频信号分量，通过周期分量反映接触压力的周期变化；高频分量用来表示吊弦点接触压力的突变，反映吊弦点接触压力的奇异特征。最后，改变接触网线索张力和线索线密度，分析接触网参数与接触压力特征间的关系。通过周期分量和高频分量，分析接触压力特征，为改善弓网受流质量，进一步提高列车运行速度提供理论基础及技术支持。

1 弓网耦合模型的建立

1.1 弓网耦合模型

为了模拟接触网各质点的运动，本文采用欧拉-伯努利梁单元建立接触网模型，该模型考虑了吊弦刚度及支持装置的影响，可以较为准确地反映接触网的垂向运动[15-16]。

接触线的运动方程为

kd(um-uc)δ(x-xn)=Fδ(x-vt)

( 1 )

式中：mc为接触线的质点质量；EIc为接触线的抗弯刚度；Tc为接触线张力；δ为冲击函数；F为弓网接触压力；，uc为接触线的垂向位移；um为承力索的垂向位移；，xn为吊弦点与运动点间的距离；x为列车运行到某一位置时的坐标；v为列车的运行速度；t为列车的运行时间。

承力索的运动方程为

kd(um-uc)δ(x-xn)+ksum(x-xs)=0 ( 2 )

式中：mm为承力索的质点质量；EIm为承力索抗弯刚度；Tm为承力索的张力；kd为吊弦刚度；ks为支柱等支持装置的等效刚度；xs为支柱点处与列车运行位置间的距离。

为了反映受电弓的高频振动，采用了可反映受电弓高频振动的三元质量模型，其运动方程为

( 3 )

式中：m1、m2、m3分别为弓头、上框架及下框架的质量；ki为受电弓各部分的等效刚度(i=1,2,3)；ci为受电弓各部分的等效阻尼(i=1,2,3)；F(t)为弓网间的接触压力；F0为施加给受电弓的静态抬升力。

本文中柔性悬挂接触网以京津城际接触网结构及单滑板受电弓为基础模型，其结构参数如图1所示。在图1中，接触线张力Tj为27 kN，型号为CuMg120;承力索张力Tc为21 kN，型号为CuMg120。在仿真软件中建立简单链形悬挂接触网及受电弓模型，受电弓的弓头、上框架、下框架及拉杆的质量分别为9.5、18.26、32.18、3.1 kg，弹簧刚度为7 200 N/m。

图1 弓网结构参数(单位：m)

1.2 仿真模型的验证

为了验证弓网耦合模型建模方法及有限元模型的合理性，本文根据BS EN 50318—2002标准[17]提供的弓网参数建立模型，将仿真结果与标准规定的相同速度下的规定范围进行对比，结果见表1。由表1可知，运行速度为250、300 km/h时的仿真结果均在标准规定的范围内。说明本文的建模方法及建立的弓网模型均是合理可行的。

表1 仿真数据与标准范围对比

2 小波变换的引入

根据建立的弓网模型，进行仿真计算，得到运行速度为300 km/h时的弓网接触压力及接触网刚度曲线，如图2所示。

图2 接触压力及接触网刚度曲线

由图2可见，受接触网刚度分布特征的影响，接触压力随跨距及吊弦间距呈周期变化。受吊弦点处刚度值及刚度变化率较大的影响，在吊弦悬挂点处出现了明显的接触压力突变，呈现明显的奇异特征。因此，采用离散小波变换，分解得到接触压力的周期分量和高频分量，其分布反映了接触压力的周期特征及奇异特征。

2.1 小波变换法

采用离散小波变换法，对接触压力信号进行处理，而信号经离散小波变换后得到的小波系数[18]为

( 4 )

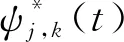
采用离散小波变换，将接触压力信号分解为不同的尺度，得到接触压力的低频信号和高频信号。低频部分表示接触压力的近似信号，亦即趋势信号。在本文中低频部分可以反映接触压力的周期变化，高频部分反映接触压力的局部信息。根据接触压力信号的频率特点，将接触压力信号f(t)进行分解，其流程如图3所示。

图3 小波分解流程

接触压力f(t)可表示为

f(t)=an(t)+di(t)i=1, 2, 3，… ( 5 )

式中：n为接触压力信号的分解层数；an(t)为低频近似信号，可以进行接触压力的周期特征分析；di(t)为高频细节信号，可以进行接触压力的奇异特征分析。

2.2 小波变换在弓网接触压力分析中的应用

Daubechies小波对不规则信号较为敏感，且具有良好的正交和频率支撑紧的特点[19]。小波分解的层数受分辨率的限制，即分解层数越少，分析越快，频带分辨率越低；反之，则相反。综合考虑，采用Daubechies小波将接触压力分解为5层，即采用Db4小波作为基小波对接触压力进行变换。

在Matlab小波工具箱中，对接触压力进行分解，得到低频信号和高频信号如图4所示。

图4 弓网接触力小波分解

在图4中，横坐标为位移，纵坐标为分解信号的值，a5表示接触压力的趋势信号，d1-d5表示接触压力的细节信号。接触压力即原始信号与趋势信号和周期信号间存在f(t)=a5+d1+d2+d3+d4+d5的关系。可以看出，a5以接触压力的跨距长度为周期，反映接触压力的跨距周期分量；d4以接触压力的吊弦间距为周期，反映的是接触压力的吊弦周期分量；d1是吊弦点处接触压力突变的分量，反映接触压力奇异特征。其他信号(d5、d3、d2)则表示多倍跨距或多倍吊弦间距周期的接触压力分量。综上所述，采用小波分解方法可以获得接触压力的周期信号及奇异信号，进行接触压力特征分析。

3 基于小波变换的弓网接触压力特征分析

由于弓网接触力整体根据接触网的跨距和吊弦间距呈周期性变化，以信号a5和d4信号为特征分量进行接触压力周期特征分析，通过d1信号分析接触压力奇异特征。接触网参数改变时，接触压力周期特征参量及奇异特征参量均将发生变化。下面通过改变接触网线索张力和线索线密度，从周期特征及奇异特征两个角度分析接触压力特征。

3.1 接触压力周期特征分析

(1)接触网线索张力变化

通过改变接触线张力和承力索张力，分析接触压力变化，选取接触网锚段中部两个跨距的接触压力数据，如图5所示。

对图5中的接触压力数据在Matlab中对其进行小波变换，得到如图6所示的接触压力跨距周期分量，图7为吊弦间距周期分量。

图5 接触网线索张力改变时的接触压力曲线

图6 接触网线索张力改变时的跨距周期分量

图7 接触网线索张力变化时的吊弦间距周期分量

从图6可知，接触网线和承力索张力增大，跨距周期分量增大，且伴随最大值和最小值沿受电弓运行的反方向移动。这是因为接触线张力和承力索张力增大，即张力增大使接触网刚度增大，限制了受电弓抬升，弓网接触更紧密，使接触压力的跨距周期分量增大。

从图7(a)可知，随着接触线张力的增大，减小了接触压力的吊弦间距周期分量。在图7(b)中，吊弦间距周期分量随承力索张力的增加而增大。这是因为增大接触线张力，吊弦间距内的刚度变化变缓；而增大承力索张力，吊弦间距内的刚度变化变快。也就是说，刚度变化率越大，接触压力的吊弦间距周期分量越大。因此，接触线张力增大，承力索张力减小，可以减小吊弦间距内的刚度变化率，从而减小接触压力的吊弦间距周期分量。

综上所述，跨距周期分量受接触网刚度的影响，接触网刚度越大，跨距周期分量越大。吊弦间距周期分量与两吊弦间刚度变化率有关，刚度变化率越大，吊弦间距周期分量越大。

(2)接触网线索线密度变化

通过改变接触线和承力索线密度，分析接触压力变化。其中接触网锚段中部两个跨距的接触压力曲线如图8所示。

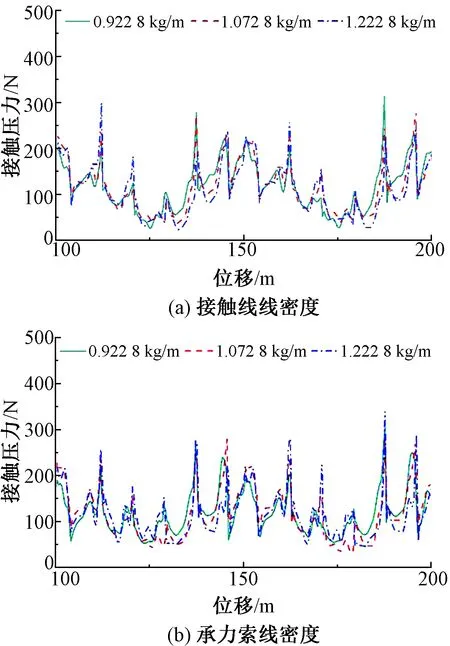
图8 接触网线索线密度改变时的接触压力

对图8中的接触压力进行小波变换，得到图9中的接触压力跨距周期分量以及图10中的吊弦间距周期分量。

图9 接触网线承力索线密度变化时接触压力跨距周期分量

图10 接触网线索线密度变化时接触压力吊弦间距周期分量

由图9可知，随着接触网线索线密度的增大，弓网接触压力跨距周期分量的最大值和最小值都向受电弓的方向偏移，且跨距周期分量的最小值减小。这是因为接触线惯性随线密度的增加而增大，使接触线质点的运动状态不易发生改变，导致跨距周期分量的最值后移。根据图8所示，受接触网惯性的影响，弓网接触压力吊弦间距分量随着接触网线索线密度的增大，基本呈增大趋势。

综上所述，接触压力的跨距周期分量及吊弦间距周期分量与接触网惯性基本呈正比例关系。也就是说，接触网线索线密度越大，接触压力的跨距周期分量和吊弦间距周期分量越大。

3.2 接触压力奇异特征分析

(1)接触网线索张力变化

通过小波变换，获得接触网线索张力变化时的接触压力高频分量，如图11所示。

图11 接触网线索张力改变时接触压力高频分量

在图11(a)中，各吊弦点接触压力高频分量的幅值及变化幅度均随着接触线张力增大而减小，也就是说接触压力的奇异性减小。这是由于接触线张力增大使吊弦点两侧的接触网刚度变得平缓，使得吊弦处接触力分量幅值幅度减小，接触压力奇异性降低。在图11(b)中，承力索张力增大，在吊弦点处的接触压力高频分量的变化幅度和幅值都明显增大，即接触压力奇异性增大。这是因为随着承力索张力增大，各吊弦点处的接触网刚度变化率增大，使各吊弦点处的接触压力高频分量增大。

综上所述，各吊弦点处的奇异性与吊弦点两侧的刚度变化有关。刚度变化率越高，吊弦悬挂点处接触压力的奇异性越大。

(2)接触网线索线密度变化

通过小波分解，获得接触网线索线密度变化时的接触压力高频分量，如图12所示。

图12 接触网线索线密度改变时接触压力高频分量

在图12中，接触线线密度和承力索线密度增大，各吊弦点的高频分量基本呈增大趋势，即奇异性增大。这是由于接触线线密度和承力索线密度的增大，增大了各质点的惯性。而吊弦作为连接接触线和承力索的连接装置，形成了质量集中点，其惯性增大更加明显，各吊弦点的接触压力高频分量增大，接触压力奇异性增大。

综上所述，各吊弦点的接触压力奇异性与质点惯性成正比例的关系，接触线和承力索的线密度越大，各吊弦点处接触压力的奇异性越大。

4 结论

本文采用小波变换方法分析接触压力的周期特征和奇异特征，讨论接触压力的跨距周期分量、吊弦间距周期分量和奇异性与接触网线索参数间的关系。得到如下结论：

(1)接触压力的跨距周期与接触网刚度和接触网质点惯性成正比例关系。接触网线索张力越大、线索线密度越大，接触压力的跨距周期分量越大。

(2)接触压力的吊弦间距分量直接受到接触网刚度变化率及接触网质点惯性的影响，即增大接触线张力或者减小承力索张力，可以减小吊弦间距内的刚度变化率，使吊弦间距周期分量减小。接触网线索线密度增大，质点惯性增大，吊弦间距分量增大。

(3)各吊弦点处接触压力的奇异性与刚度变化率及质点惯性成正比例关系，即增大接触线张力或者减小承力索张力，使各吊弦点接触压力奇异性降低。增大接触网线索线密度，将使各吊弦点处接触压力的奇异性增大。