基于累积前景理论的高速铁路差异化定价与坐席分配联合优化方法
秦 进,吴志君,杨 康,毛成辉,黎熙琼,CHANTHAVONG Vanpadith
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.轨道交通大数据湖南省重点实验室,湖南 长沙 410075)
我国高速铁路(以下简称“高铁”)营业里程已近4万 km,路网规模、运输密度等均居世界首位。根据统计资料,2019年我国高铁动车组发送旅客同比增长14.1%,至22.9亿人次,占全路旅客发送量64.1%[1],这表明高铁已经成为我国铁路旅客运输的主力。但目前高铁的市场化运营水平相对航空、汽运等仍比较落后,尤其是客票定价还未能充分考虑市场需求特征,无法实现客流的有效引导和调节,导致热门车次供不应求和冷门车次供过于求的情况同时存在,造成一定程度上的高铁运输资源浪费,也降低了高铁服务水平和企业收益。
差异化定价是指对具有可替代性的多个产品制定不同的价格,调节供需匹配关系,从而实现服务水平和企业收益最大化的一种商品销售定价策略,如法国高铁允许同一起讫点(Origin-Destination, OD)的列车根据旅行时间、发车时段以及服务水平等因素设置不同的价格。目前我国高铁正进行市场化运营的改革探索,在票价方面,也开始有学者尝试通过对高铁列车实施差异化定价,以达到调节客流、提高列车上座率的目的。Van[2]根据边际成本理论研究铁路客运最优定价决策,建议铁路在不同发车时段采取不同票价;尹少成[3]指出铁路应借鉴航空领域市场化经营经验,列车票价应随发车时段、购票时间等因素波动;王灿灿等[4]提出应根据运输淡旺季的客流峰值不同,进行季节性的差异化定价;文献[5-8]基于列车属性特征的不同,以平衡列车能力利用率和实现系统效益增收为目标,构建多列车差异化定价方法。
由于客票定价与坐席分配之间存在密切联系[9],因此将两者进行联合优化正成为当前的研究热点。既有研究多基于随机效用理论或期望效用理论,假设旅客完全理性,构建相应优化模型,如赵翔等[10-11]考虑随机需求特征,分别构建单交通模式和多交通模式下的平行车次差异化票价票额综合优化模型;宋文波等[12]提出固定需求环境下的多列车差异化票价和票额的综合优化方法;Hu等[13]通过形式票价描述坐席分配策略,有效降低问题规模。但这些研究在描述旅客行为时往往忽略旅客出行特征的不同。
出行特征是旅客选择行为的主要影响因素之一[14],Espino等[15]指出忽略旅客出行特征不能准确描述旅客选择行为,从而导致高估所得优化方案的效果。部分学者为解决这两个问题做出了尝试。Qin等[16]利用前景理论描述旅客的有限理性,但是由于前景理论自身局限性,模型适用范围较小。文献[10,17-18]也有意识地考虑旅客出行特征,但模型中对于出行特征的体现不够全面,均只涉及部分内容。
综上所述,在高铁差异化定价的既有研究中,对于旅客决策行为的非完全理性和旅客出行特征均考虑较少。行为科学领域中的累积前景理论(Cumulative Prospect Theory, CPT),在保留前景理论能够刻画有限理性的优点的同时,利用累积变形概率函数实现了理论大范围适用和满足一阶随机占优现象,因此在高铁差异化定价问题中引入CPT更具优势。从理论层面看,高铁票价影响需求,坐席分配决定供给,将票价和坐席分配进行联合优化,是充分考虑供需匹配关系。从实践层面看,高铁票价制定与坐席分配相互联系不可分割,在定价问题中联合优化坐席分配,可进一步提升客票总收益,同时也可在一定程度上,避免实际需求与坐席分配方案相差较大,从而给工作现场带来大量临时调整工作[9]。本文基于历史客票数据分析旅客出行特征并进行旅客分类,利用CPT描述每类旅客出行选择行为的有限理性,在此基础上以客票总收益最大化为目标,提出弹性需求下高铁差异化定价和坐席分配的联合优化方法。
1 变量定义及问题分析
旅客根据高铁票价、旅行时间、发车时刻等多个因素进行列车选择,最终形成多列车多OD间的客流分布。差异化定价的目的,在于给高铁列车制定有差别的票价,引导客流转移,形成新的票价水平下的客流分布状态,使得列车之间的客流需求更为均衡,提高运力资源的利用效率和总收益的增长。
客流需求规律是进行科学差异化定价的基础[19]。为准确描述高铁旅客客流需求规律,需要深入分析高铁旅客的出行特征。旅客出行特征主要包括出行目的、出行距离、出行时间和出行费用[20]。这些因素的细微差异,都可能会影响具体旅客的出行选择决策。因此对每位旅客个体进行单独的选择行为描述是无法实现的。本文根据上述因素对旅客出行行为的影响规律对旅客进行分类,在此基础上刻画每类旅客的选择行为。
另外,相关研究表明,旅客在出行选择过程中的有限认知能力和逻辑推理能力,使得其决策过程呈现出有限理性的特征[21],例如,旅客的出行决策都存在参照点依赖,并更倾向于追求低概率的“高价值获益”和避免低概率“高价值损失”,同时旅客对损失的规避程度和对相同程度获益的偏好程度也并不相同,但都厌恶损失[22-23]。
CPT是Tversky等[24]提出的描述性决策理论,认为有限理性的自然人是极大累积前景效用的追求者,累积前景效用是所有可能情形下价值函数值与累积概率值的乘积之和,价值函数与累积概率函数均是实际结果和决策人内心参照点偏离程度的函数。CPT理论主要贡献在于将参照点作为价值曲线原点来体现参照点依赖,利用不对称性的价值曲线反应厌恶损失,采用累积变形的概率函数解释人追求小概率事件的心理,利用CPT可以较好解释人在决策过程中的有限理性。因此本文根据客票数据对高铁旅客进行分类,基于CPT理论进行不同类旅客的出行选择行为的有限理性特征刻画。
本文研究的问题可以描述为:针对给定的高铁线路,首先根据旅客出行特征进行旅客市场细分,并准确刻画各类旅客出行行为的有限理性选择特征,在此基础上构造科学的高铁旅客弹性需求函数,以客票总收入最大化为目标,充分考虑列车运输能力(坐席数量)、票价水平区间和票价不倒挂等约束,求解线路上服务各OD间的各高铁列车的最优票价和和相应的最优席位分配数量。为简化问题,做出以下合理假设:
(1) 列车开行方案已经给定且不发生变化。
(2) 按照旅客先到先得的规则服务,超出票额限制的出行需求将不被满足。
(3) 旅客出行需求主要受票价、旅行时间、发车时刻和退票成本4个因素影响。
(4) 不考虑列车席位等级。
为方便后面描述,符号及定义见表1。

表1 符号及定义
2 旅客分类
出行特征是旅客选择行为的主要影响因素之一,不同出行特征的旅客选择行为呈现一定的差异[14]。本文依据出行特征对旅客进行分类,将出行特征类似的旅客归为一类,为后续弹性需求函数的构建奠定基础。高铁的历史客票数据包含着大量旅客行为信息,可以直观反应旅客的旅行时间、出行距离和出行费用,尽管出行目的在客票数据中无法直接体现,但旅客的出行日期和提前购票天数可以从侧面和局部反映旅客的出行目的。因此,本文考虑从历史高铁客票数据中选取出行日期、提前购票天数、旅行时间、出行距离、出行费用5个外显变量,利用潜在类别模型实现考虑旅客出行特征的旅客分类。
潜在类别模型是一种将潜在变量理论和分类相结合的统计分析技术,利用最少的潜在类数目解释外显变量之间的联系。既有研究多利用潜在类别模型对给定高铁线路所有OD服务的所有旅客同时分类,仅能处理小规模数据,在客票数据超过5万条时分类效果难以满足要求[25]。此外由于客票数据中仅包含高铁的出行费用和旅行时间,而目前高铁出行费用和旅行时间都与出行距离密切相关,因此对所有旅客同时分类的方式,会忽略距离相近但备选交通方式集不同的OD间出行费用、旅行时间的差异,从而不能准确反映旅客出行特征。以京沪高铁为例,济南西—南京南和北京南—南京南的距离相差不大,但济南西—南京南无直达航班,组合出行费时又昂贵,因此绝大多数旅客都会选择高铁出行,因此该OD间旅客备选交通方式主要为公路和铁路。而北京南—南京南之间有直达航班,备选交通方式有公路、铁路及航空。这两个OD间旅客的备选交通方式的旅行时间集合、出行费用集合显然有较大差异,在旅客类别细分时必须加以考虑。
本文以历史客票数据为基础,对每个OD间的旅客进行单独分类。因为对于同一OD间的旅客,其出行距离相同,可选交通方式相同,所以旅客备选交通方式的旅行时间集合与出行费用集合组成是相同的。在后续旅客选择行为描述中,通过不同的参数取值即可体现各OD间旅行时间、出行距离和出行费用不同给旅客带来的影响,因此这3个外显变量在旅客分类过程中不予考虑。再利用剩余出行日期A、提前购票天数B两个能够从侧面反应出行目的的外显变量,对每个OD间的旅客进行单独分类以区分出行目的,即可实现在模型中全面考虑出行特征的主要内容。对每个OD间的旅客分类,也是对历史客票数据的降维,可以处理更大量级的数据。
选取好外显变量之后,提取的数据并不能直接用于分类,需要对所有外显变量数据进行处理,以不同的数字表示各外显变量的不同取值。借鉴文献[25]思想及高铁退票费率,分别对出行日期和提前购票天数分段进行适当调整。分水平处理结果见表2。

表2 分水平处理结果
根据潜在类别模型框架[25],对于外显变量组合为{a,b}的旅客,属于潜在类别i的分类效用值Uabi为
a=1,2,…,7b=1,2,…,5
( 1 )

( 2 )
外显变量组合为{a,b}的旅客属于潜在类别i的概率P(i|{a,b})为
( 3 )
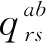
( 4 )
( 5 )
( 6 )
3 弹性需求函数构建
考虑到高铁网络中任意列车票价的变化,会影响系统内所有客流需求的时空分布,进一步又会影响多趟相关列车的需求分担比例。因此不宜单独确定单趟列车需求与其票价之间的弹性关系[10]。考虑到OD间的总需求与不同列车需求之间的内生关系,可以分2步确定列车的弹性需求函数,首先构建任意OD间的各类旅客总需求的弹性函数,然后建立服务该OD间所有列车的各类旅客需求分担比例函数,对各类需求求和即可获得不同列车的客流需求量。使用累积前景效用描述旅客出行行为的关键,在于构建出行效用函数和参照点。
根据累积前景理论,旅客是极大累积前景效用的追求者。累积前景效用的计算与高铁出行效用、旅客内心参照点相关。累积前景效用的计算过程见图1。
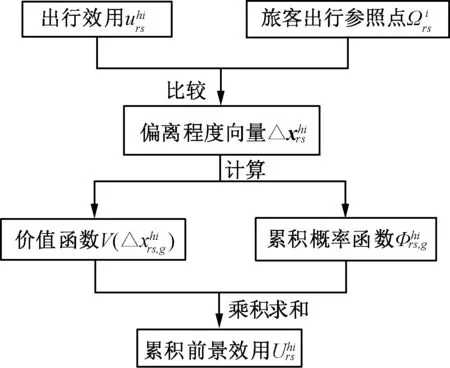
图1 累积前景效用计算过程
(1)高铁出行效用函数
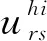
( 7 )
( 8 )


( 9 )

考虑现实中旅客对于出行效用微小差异的辨别能力十分有限,可利用离散分布拟合效用的连续分布[21]。舍弃高铁出行效用连续分布两侧的小概率极端取值,保留一定置信水平y%下中间的置信区间。然后将置信区间等距分割成K份,认为该等距分割段的中值与该段其余值仅存在微小差异,可以取中值代表该等距分割段,作为高铁出行效用波动的一个结果。由此,得到高铁出行效用向量表达为
(10)
每一等距分割段上的概率分布值作为相应波动结果出现的概率,得到概率向量为P=(P1,…,PK)。
(2)出行决策参照点

(11)
s.t.
(12)

(13)
(3)高铁出行需求弹性函数

(14)

1≤g≤K
(15)
式中:α、β(0<α≤1,0<β≤1)用于判断远离参考点的敏感性变化,α、β的值越大,出行者对风险的感知越强;λ为损失规避系数,且始终存在λ>1,体现了决策者对损失的敏感性更强。
累积概率函数是描述旅客对客观风险概率的反应程度,用参数δ反应累积概率函数的曲率。旅客的累积概率φ(P)为
(16)
(17)

(18)
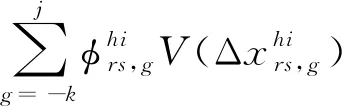
(19)
(20)

(21)
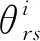

(22)
对所有类旅客求和,即可得到列车h的价格弹性需求函数为
(23)
4 联合优化模型

以期望总客票收益最大化为目标,构建高铁差异化定价与坐席分配联合优化为
(24)
s.t.
(25)
m∈[1,N-1]h∈Hrs
(26)
(27)
(28)
(29)
h∈Hrs
(30)
(31)
h∈Hrs
(32)
模型中,式(7)体现了根据旅行时间、发车时段等不同因素对列车差异化定价的影响,由差异化价格调节需求;式(24)、式(25)体现了差异化定价和坐席分配的联合优化;式(26)为列车运输能力约束;式(27)为票价上下限约束;式(28)、式(29)表示对于同一到站或同一发站,较长区段的票价应高于较短区段的票价,避免产生票价倒挂现象;式(30)表示长区段票价应不小于其他可以拼接成该区段的各较短区段的票价之和,避免旅客多段拼接购票或者“买短+上车补票”;式(31)表示坐席分配取值下限,τ为最小满足客流需求比例,避免一味追求最大利益而致使某些OD不分配坐席数量;式(32)表示决策变量的取值范围。
5 模型求解
5.1 基于多段映射罚函数的模型转化
模型中式(28)~式(30)是有关票价的关键约束,为求解算法设计带来了困难。可以采用非固定多段映射罚函数对其进行转化处理,以避免罚函数法中难以确定罚因子难题[30]。
构造广义目标函数为
(33)

惩罚力度与惩罚项的更新公式为
(34)
(35)
(36)
(37)

上述联合优化模型属于混合整数非线性规划,并且票价和预期售票数量组合维度大,基于CPT构造的弹性需求函数含有正态分布和多次非线性变化,一般优化算法难以在有效时间内求取高质量的最优解。基本灰狼算法(Grey Wolf Optimizer, GWO)是一种全新的群智能优化算法,通过模拟狼群狩猎行为实现优化,由于全局搜索能力强、调整参数少等优点,在工程领域应用广泛[31-32]。本文结合所研究问题的特征,在对基本灰狼算法进行改进的基础上,设计求解方法进行计算与分析。
5.2 GWO算法基本思路
GWO算法的基本原理,是狼群中每一只狼位置信息代表问题的一个解,最容易捕获的猎物位置代表优化问题的最优解,狼群逐渐靠近猎物实施抓捕,即不断优化获得最终解的过程[31]。首先通过随机的方式,在可行域范围内随机生成初始狼群位置,对每一个体灰狼位置进行适应度值计算。根据适应度值将狼群划分为4个等级,狼群中位置最优个体、次优个体、次次优个体分别记为记为G1、G2、G3,其余灰狼均为低等级狼G‘。
在迭代过程中,G1、G2和G3被认为是3只高等级狼,拥有获取猎物位置的潜在能力,高等级狼共同指导所有低等级灰狼G‘进行位置移动。捕食过程前期,狼群离开当前猎物位置前往别处搜寻更容易捕获的猎物,即进行全局搜索;到了后期,狼群逐渐靠近当前猎物实施抓捕,进行局部搜索。
算法执行中通过线性变化的距离控制参数d来影响狼群采取何种行动。狼群位置每更新一次,重新计算适应度值,根据适应度值更新高等级狼的位置,新的高等级狼继续指导狼群移动,循环往复,直至捕猎行为结束。当算法迭代结束时,G1狼的位置代表优化问题的最终解。
5.3 GWO算法的改进
GWO存在以下几处不足:首先,初始狼群位置随机生成,狼群位置分布并不总是均匀的,而既有研究已证明初始种群均匀分布能提升群智能算法的寻优能力[33];其次,线性变化的距离控制参数d并不能始终很好地平衡算法全局搜索能力和局部搜索能力;最后,算法中缺乏陷入局部最优后的跳出机制。针对上述不足,对GWO算法进行改进。
(1)初始狼群的改进
利用佳点集策略生成均匀分布的初始狼群。任意给定一定数量的点,用这些点的函数值构成的任何加权求和形式来近似计算函数在欧式空间单位立方体上的积分时,所取得的误差最小的点集称为佳点集。佳点集本质上是一个均匀分布的点集。将欧式空间单位立方体上的佳点集映射到求解空间能够使初始狼群在解空间中均匀分布。记问题决策变量维数是Dim,取Q个点的佳点集Dn(m)用以狼群初始化。
Dn(m)={({exp(1)×m},{exp(2)×m},…,
{exp(Dim)×m}),m=1,2,…,Q}
(38)
式中:{exp(·)×m}为exp(·)×m的小数部分。Dn(m)佳点集的每个分量均在[0,1]之间,为了将单位立方体上的佳点映射至解空间,还需要将佳点集进行映射处理。映射f为
f[exp(g)×m]=lbg+{exp(g)×m}×(ubg-lbg)
(39)
式中:lbg、ubg分别为第g个分量的取值上下限。对佳点集Dn(m)中每个佳点的每个分量执行映射f,即得初始狼群。基于此方法构造的初始狼群隐含票价上下限约束,能保证票价在上下限范围内均匀取值。
(2)距离控制参数的改进
灰狼算法中距离控制参数d的设置,影响着算法全局搜索能力和局部搜索能力的平衡。可以考虑使参数d非线性递减以提升算法性能,即在迭代的前期,选择较大的d值可提高全局搜索能力以避免算法出现早熟收敛的情况;迭代后期,有较小的d值可以让狼群在某区域内集中搜索,加强局部搜索能力。
(40)
式中:iter和itermax分别为当前迭代次数和最大允许迭代次数。
(3)最差位置改变策略
基本灰狼算法没有考虑陷入局部最优之后的跳出策略,因此本文借鉴随机蛙跳算法[34]对适应度最差蛙的位置改变策略对灰狼位置更新方式进行改进。在每一次迭代过程中,计算每个灰狼个体对应的适应度值,记录最差适应度值的灰狼个体。引入蛙跳概率Pfrog,在每次迭代过程中生成随机数和Pfrog的值进行比对。当随机数大于Pfrog时,最差灰狼个体按基本灰狼算法更新位置;当随机数小于等于Pfrog时,最差灰狼个体按照式(41)更新自身位置,即最差灰狼个体跳出当前解,根据最优灰狼位置去寻找更优解。
(41)

5.4 算法步骤
具体算法步骤如下:
Step1根据给定线路,从历史售票数据中获取列车开行方案、固定票价下客流量等数据。设置模型和算法所需的参数。
Step2初始化算法迭代参数。当前最优适应度值Fmax=-∞,迭代次数iter=0,3只高等级狼G1、G2和G3的位置向量设为零向量。
Step3初始化狼群。根据佳点集理论初始化灰狼种群,每一只灰狼的位置向量对应一组票价集合。

Step5G1、G2和G3适应度值及位置向量更新。将当前代灰狼种群的适应度值与G1、G2和G3的适应度值进行比较,更新G1、G2和G3适应度值以及对应的位置向量。
Step6狼群位置更新。根据式(40)计算距离控制参数,更新灰狼位置向量;同时按照蛙跳概率Pfrog更新最差灰狼位置使其能跳出局部最优。
Step7判断算法是否满足收敛条件。如果是则算法终止,输出最优票价组合G1位置向量及其对应最优坐席分配方案,输出最优客票收益值Gα对应的适应度值;否则返回Step4继续迭代。
6 算例分析
以京沪高铁下行(北京南往上海虹桥)的G1、G3、G5、G7、G11、G13、G15、G17共8列车为研究对象进行计算分析。当前运行图中各列车的停站方案见图2。为避开假期等特殊时期对客流的影响,选取2017年6月1日至30日作为数据统计时段,将每趟列车的日平均客流量作为算例的初始客流需求。

图2 停站方案
6.1 旅客分类结果分析
为了便于求解和保证结果合理性,需要找出既具有较少类别,又具有较好拟合优度的旅客分类结果。进行拟合优度检验的主要方法有似然比卡方统计量检验G2、Pearson 检验χ2,基于似然比卡方检验的信号评价指标AIC和Bayesian信号评价指标BIC。这里将上述4种指标结合起来进行模型拟合优度的评价,指标越小表明模型适配度越高。利用Latent Gold软件对潜在类模型进行求解,将潜在类别个数从1开始逐个增加至5,结合BIC、AIC、χ2、G24种评价选取最终潜在类别个数。以OD对北京南—上海虹桥为例,潜在类模型检验指标输出见表3。随着潜在类别个数的增加,指标χ2、G2一直下降;而BIC、AIC先下降后又升高,分别在潜在类别个数为4和5的时候达到最小值。当数据量较大时,BIC是主要参考指标,因此北京南—上海虹桥最佳潜在类别个数为4。

表3 北京南—上海虹桥潜在类模型检验指标
不同OD对之间达到最优拟合效果的潜在类别个数并不完全相同,算例中所有OD的最优潜在类别见表4。

表4 各OD最优潜在类别数目
对于最优潜在类别为1的OD对,表明在算例研究范围内该OD对的全体旅客出行特征都类似,不需要额外进行分类。对于其余OD对,考虑到多个潜在类别会增加联合优化模型的求解复杂度,且模拟结果中这些OD潜在类别为2时BIC的值与最小值相差均不超过1%,故本文将这些OD旅客分为2类,即潜在类别数目为2。以济南西—上海虹桥为例,潜在类别数目设置为2时,参数拟合结果见表5。

表5 济南西—上海虹桥潜在类模型参数拟合结果
将2类旅客分别命名为公务型旅客和休闲型旅客。从参数拟合结果来看,该OD对旅客以类别1为主,占比达64.45%。类别1旅客的显著特点是倾向于在工作日出行,一般较晚购票,计划性较弱,此类旅客的出行目的偏向于公务出差,因此命名为公务型旅客;而类别2旅客倾向于周末出行,提前较长时间进行购票,计划性较强,这些特征表明该类旅客出行目的偏向于休闲旅游,因此命名为休闲型旅客。
6.2 结果分析
所得的最优方案中,8趟列车的总客票收益为4 528 824元,较原始固定票价下的总客票收益(4 326 914.5)元增加了4.67%,优化后票价结果见表6。从表6可知,相对于初始票价,不同OD对的票价有不同的波动情况。北京南—上海虹桥运输距离长,同时有直达航班,旅客需求弹性大,各列车通过降价的方式吸引更多旅客进行购票。而北京南—济南西运输距离超出了公路的优势运距范围,且没有直达航班,旅客需求弹性较小,各列车票价上涨以达到提升收益的目的。值得注意的是,同一OD对各列车差异化定价结果,并不完全取决于该OD间初始客流需求的分布。以北京南—济南西为例,G15初始客流需求仅为19人,但优化后票价上涨了18.16%。这是因为G15大量席位被分配给北京南—上海虹桥的旅客,仅有少量席位可供北京南—济南西的旅客预定。因此G15在北京南—济南西票价上涨,正是通过票价调节需求,使得旅客选择其他高铁列车。这从侧面说明了高铁差异化定价是一个复杂的组合优化问题,最终票价结果需综合考虑所有OD需求在各列车之间的分布情况。

表6 优化后票价 元
将最大值与最小值之差与平均值的比值定义为差异值,用以衡量各列车优化后票价的差异大小。不同OD对不同列车之间优化后票价差异见表7。由表7可知,在具有多趟列车的6个OD对中,优化后的票价差异比较明显,始终处于[5.83%,28.67%]。

表7 优化方案票价差异值情况 %
票价发生变化,各OD的客运需求也发生改变,因此各OD的票额分配数量也相应变化,最终实现列车发送旅客人数变化,各OD总客流变化情况见表8。由表8可知,在差异化定价方案下,总发送客流量呈现上升趋势。从不同OD 来看,差异化定价方案下长途客流增加,短途客流减少。在采取单一票价时,由于费率采取递远递减的梯度设置,在短途客流能完整裂解全程席位的情况下,分配短途票额能使收益达到最大化。但是在差异化定价条件下,单位费率并不一定符合递远递减的梯度原则。并且短途初始票价不高,客流需求弹性系数也相对更小,同等比例的票价变化幅度对短途客流需求调节力度相对更弱,票价对客流的调节作用并不总能实现大量短途客流完整裂解全程席位。结合表6的票价优化结果,差异化定价方案倾向于以低票价吸引长途客流,以最大程度利用列车运输能力,发挥高铁运距长的优势。

表8 各OD总客流量变化情况
差异化定价提升客票收益的关键在于提高列车能力利用率。票价优化前后,各区段列车客座率对比情况见表9。由表9可知,优化之后更多区段趋于饱和,部分车次在部分区间客座率有明显提升。结合表7中各OD总客流量变化可知,长距离OD客流量增加足以弥补短距离OD客流量的部分减少,从而使得各区段客座率有不同程度提升,部分区段甚至所有列车的客座率均达到1。

表9 不同列车不同区段客座率变化情况
各区段列车客座率的方差见图3。由图3可见,从列车客座率的方差角度来看,每个区段列车客座率方差均显著减小,这说明不同列车客座率之间的差异减小,差异化定价充分发挥了客流调节作用,使得旅客在不同列车之间的分布更为平衡。

图3 客座率方差
7 结论
固定票价无法有效调节高铁客流,可替代列车之间客座率相差较大,造成运输资源浪费,未能充分挖掘高铁盈利能力。本文着眼于该实际问题,从不同高铁列车之间的可替代性出发,对高速铁路差异化定价进行了研究。首先,利用潜在类别模型对旅客进行分类。其次,引入CPT构建差异化定价下的弹性需求函数。之后,构建高铁差异化定价和坐席分配的联合优化模型,并设计改进的灰狼算法对模型进行求解。最后,通过数据实例验证模型和算法的有效性。主要结论如下:
(1)与既有方法相比,本文考虑了出行特征不同给旅客选择行为带来的影响,体现了差异化定价背景下旅客决策的有限理性,从而使得构建的弹性需求函数更贴近真实情况,对于铁路企业市场化改革更具借鉴意义。
(2)京沪高铁算例的数值验证结果显示,本文方法所得各OD间各列车之间票价差异明显,坐席分配方案科学合理。在不投入更多运输资源的同时,差异化定价与坐席分配联合优化可使企业客票收益上涨4.67%。本文研究成果能指导铁路企业灵活定价和科学分配坐席数量,有助于提高服务水平,扩大收益,实现企业健康长足发展。
(3)高铁差异化定价是复杂的组合优化问题,某OD间某列车的票价优化结果并不仅仅取决于该OD间初始客流需求,而是多OD间多列车共同作用的结果。因此,多OD间多列车定价问题研究更具意义。
(4) 差异化定价对客流有明显调节作用。票价优化后,各OD间客流量产生明显变化。长途旅客相较于短途旅客,弹性系数大、初始票价高,在运输资源较为充裕的前提下,差异化定价方案更倾向于以低票价吸引更多长途旅客,从而提升客票收益。差异化定价方案有利于发挥高铁在中长途运输中的运距优势。各列车区段客座率有明显提升,多个区段能力趋于饱和。同时,各列车区段客座率方差显著减小,说明差异化定价后旅客需求在不同列车之间分布更为均匀。

