基于多元线性回归的新车型投产时间预测研究
徐雯霞 黄世杰
(同济大学,上海 201804)
0 引言
汽车产品的销量逐年递增,随之而来的产品质量投诉也日益增多。由2021年车质网的统计报告可知,汽车的投诉量在2010—2020年间增长了近50倍,其中有约40%的投诉内容来自整车产品质量问题。这既反映了国内消费者对汽车产品的质量要求和期望在不断提高,也说明了为了加快新车型的上市速度,大部分车企很有可能在产品设计或生产工艺上没有做好充分验证。
投产又称为新项目导入,即企业把概念化和数字化的设计转化为规模化量产的消费产品,主要任务是按时实现质量达标的整车产品以及配套达标(设计产能、稳定性)的生产线的量产,并实现高效率生产的经济效益。投产环节紧密衔接设计—制造—质量,可有效验证产品设计缺陷、防堵制造工艺漏洞、试错作业员可能存在的操作失误,使生产线上的新工艺和新员工顺利完成磨合和爬坡,使整个产品线高效稳定运行。这是汽车产品成功投放市场、维护品牌良好口碑必不可少的环节。
1 新车型投产时间的影响因素
目前,各大合资车企对投产时间的预测仍以经验总结和专家评审的方式为主,虽然欠缺科学性的论证,但仍然具有较高的参考价值。很多车企在制订新车型投产计划时会进行专家评审,并充分结合之前新项目投产时积累的经验,尽量避免以过多的假设承担计划外的风险[1]。分解并罗列投产阶段的关键路径以及影响其所需要的时间的行为,即可得出影响投产时间的关键因素。PT1和PT2的持续时间和需要验证的工艺站点数量和复杂程度相关,所以“新工艺设备验证”也是投产时间影响因素之一。对各类型合资车企影响投产时间的因素进行总结,见表1。
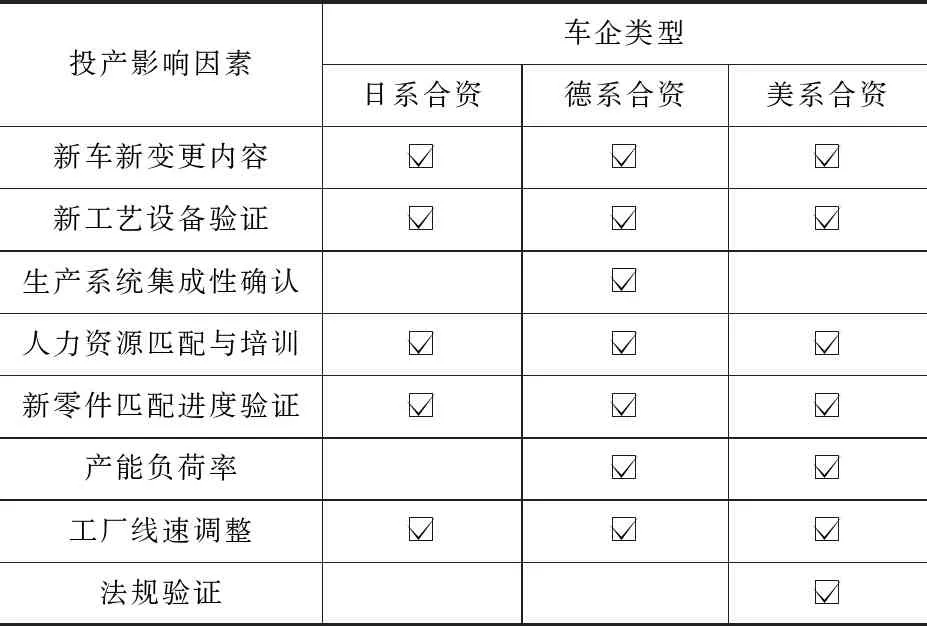
表1 影响投产时间的因素
2 新车型投产时间预测模型构建
通过对投产阶段关键步骤的调研与归纳,结合福特汽车的投产管理模型(LQOS),构建新车型投产时间影响因素的数据库:上车身变化为X1,下车身变化为X2,动力总成变化为X3,工厂线速或生产节拍为X4,工厂班次为X5,新车型投放市场的数量为X6,工厂在产车型的数量为X7;因变量Y为投产所需的时间(以周为单位)[2]。将过去5年间投产的新车型的投产数据作为模型样本,新车型投产时间统计见表2。

表2 新车型投产时间统计
其回归模型为:Y=β0+β1X1+…+β7X7+ε。其中,βn是未知参数,称为回归系数;ε是均值为0、方差为σ2(σ>0)的随机误差,代表其他随机因素对投产事件Y产生的影响。对于总体(X1,X2,…,X7;Y)的n组观测值(x11,x22,…,x77;yi)(i=1,2,…,7),线性回归模型可用矩阵表示为:Y=Xβ+ε。
利用SPSS软件计算多元线性回归模型,对线性回归方程进行求解,如下
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT投产时间
/METHOD=ENTER车身 底盘 动力总成 节拍 班次 市场数量 在产车型
/SCATTERPLOT=(*ZPRED,*ZRESID)
由SPSS的计算结果分析:
(1)调整后R方为0.73,也就是说明在所选自变量中能够解释因变量投产时间变化的73%,也就是说投产时间的变化情况中有73%是由于以上变量影响造成的。在统计学中只要变量影响达到30%就代表关系成立,所以所选参数设置是可以被接受的。
(2)德宾-沃森值为1.679,接近2,说明方程各自变量之前自相关性可以被接受,但数值与标准值仍有所偏差,暂时猜测为某一个或者几个变量可能存在一定的自相关性或者共线性。
(3)方差分析结果(ANOVA),模型的P值(显著性)为0.00,远小于0.05,证明模型至少含有一个自变量对因变量Y(投产时间)存在显著影响,所以此模型显著性关系成立。
由此得出以下回归方程,用于表示因变量投产时间与自变量影响因素之间的关系
y=2.548x1-0.981x2+1.997x3-0.078x4+2.881x5+0.047x6+0.111x7+17.763
方程系数的解集见表3。
各个数据的VIF值除了“下车身变化”,其余自变量的VIF值均小于5,见表3(严格的统计学意义中,VIF小于5说明变量之间没有强烈的共线性),说明除了“下车身变化”可能与其他变量存在共线性,其余变量均为相互独立的自变量。表3中上车身与动力总成变化的显著性分别为0.002和0.004,远小于0.05,说明上车身变化量能够显著影响投产时间的长短,同时系数分别为B1=2.548、B3=1.997。也就是说,上车身和动力总成的变化范围与投产时间成正比,符合模型之前的原假设,这两个变量X1和X3对于方程成立。
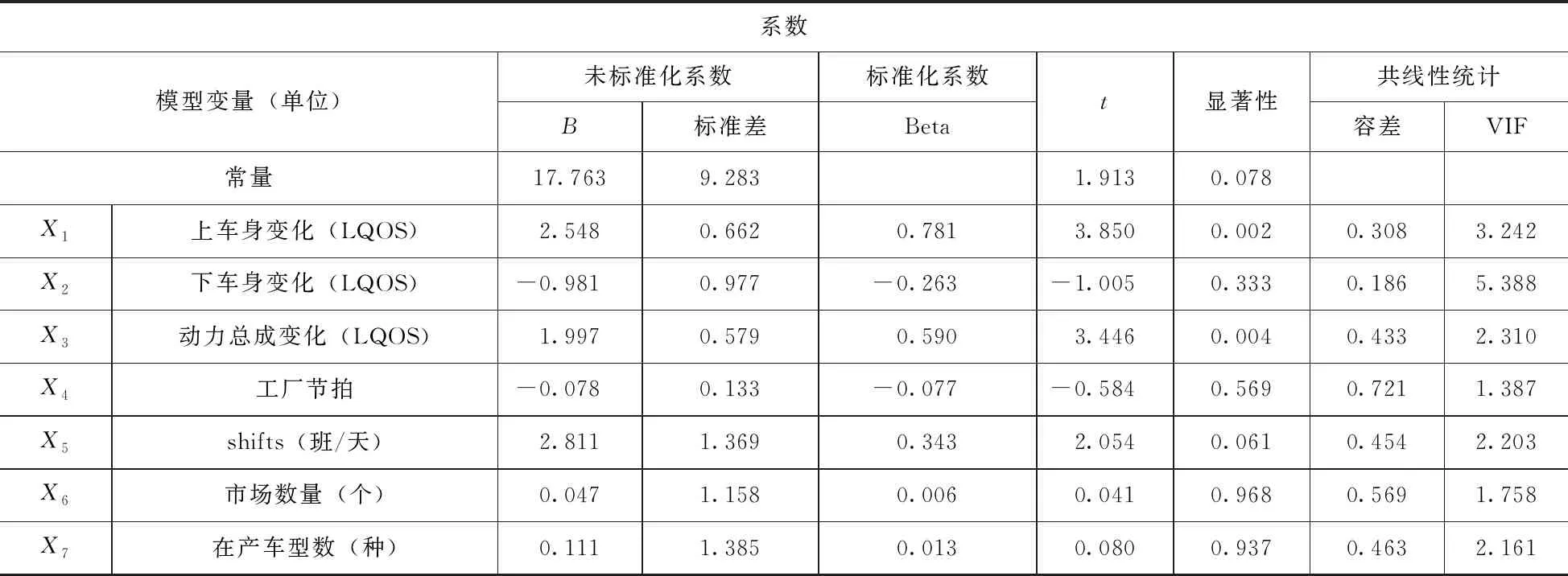
表3 方程系数的解集
另一个变量X5班次的显著性参数为0.061,也非常贴近0.05。考虑到样本数量存在不够充分的潜在缺陷,暂时认为此变量也对因变量Y投产时间有显著影响。系数B5=2.811,为正值,也与模型原假设一致,故也可认为其成立。
自变量下车身变化X2和生产节拍X4对于方程不成立,因为这两个自变量的系数计算结果为负数,与原假设和实际情况不符,即下车身变化范围和工厂节拍越大,投产所需的时间越长。同时,下车身变化也不满足统计学共线性(VIF<5)的指标。
3 残差分布分析
标准化残差的直方图如图1所示,显示残差值分布集中于-1.5~1.5,不吻合正态分布,因此按照这些样本分析出的模型并不能很好地匹配自变量和因变量的关系,此线性回归模型存在问题,有可能是问题变量所造成的,即“下车身变化”和“工厂线速或生产节拍”。
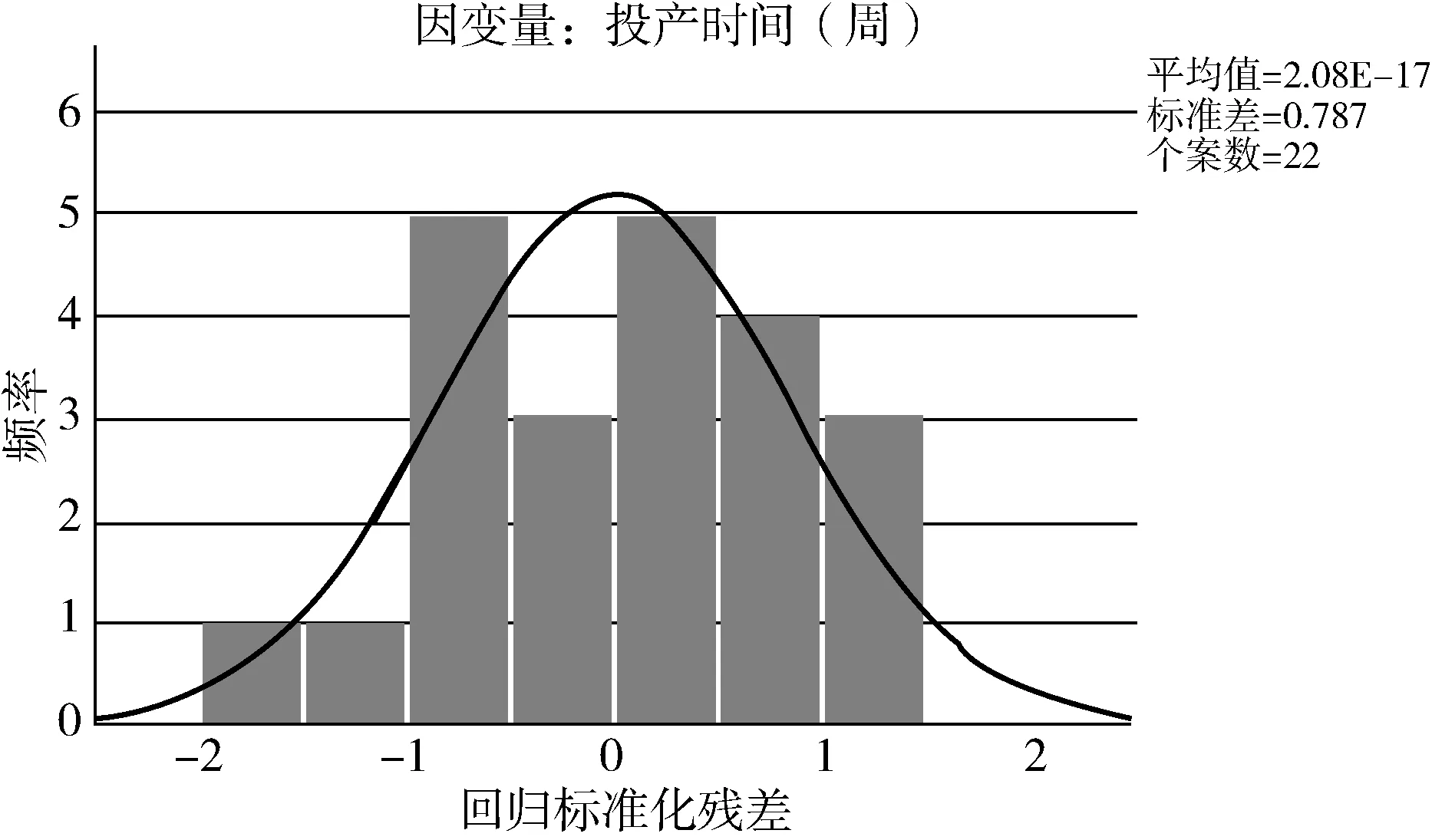
图1 标准化残差直方图
4 预测模型的修正
删除问题变量进行变量调整[3],重新利用SPSS计算。调整后模型R方为818,相较调整前R方835并没有因为变量的减少而降低,反而增大了,有可能是因为去除了干扰的无效变量反而使得模型更能契合自变量对因变量造成的影响。同时,德宾沃森指数由1.697增大为1.841,调整后的模型比原模型更接近2,说明新的模型比原模型的自相关性更低,优于原假设。
调整后的模型显著性为0.000,小于原模型的0.001,远小于0.005,说明显著性上更新的模型也要优于原模型。
修改后的模型VIF值均小于5且远小于原模型,因此说明各个变量基本不存在共线性,更新后的模型和自变量切合度更高,同时变量对应的系数均为正值,这也符合原假设即这些自变量均与因变量成正相关性。
相较于原回归模型的直方图,修正后的模型残差更贴近于正态分布,如图2所示。表示模型预测出现误差的概率更趋于随机性或者意外性,从而证明利用修正后的模型具有更高的概率预测出实际的自变量和应变量的变化关系,模型的残差正太分布可以被接受[4]。线性回归方程按照修正后的模型系数解得
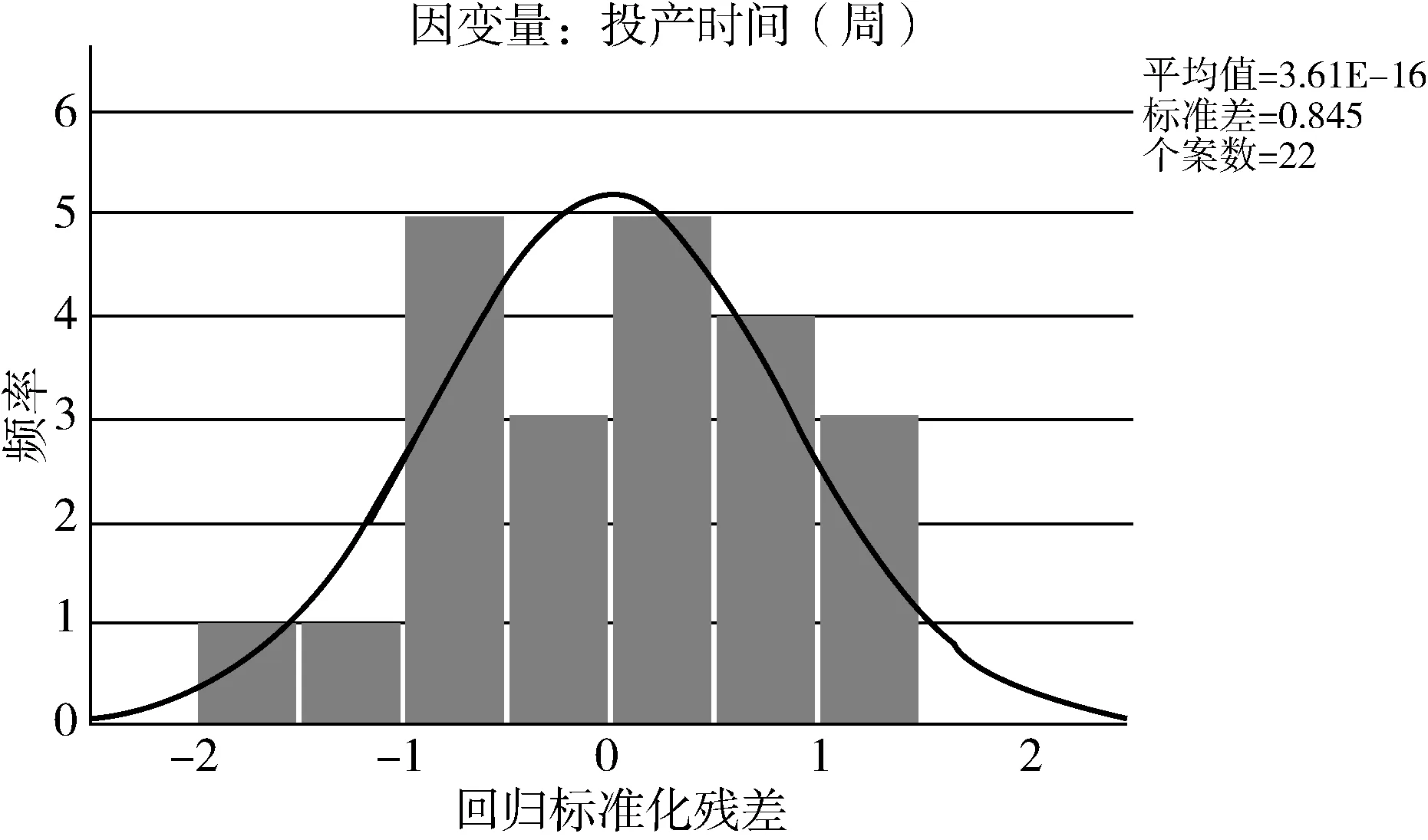
图2 调整后模型残差直方图
y=2.804x1+1.619x2+1.927x3+0.635x4+0.79x5+14.082
5 误差变量分析
在实际案例中,下车身的变化往往不会单独发生,而是与上车身变化或者动力总成变化同时发生,或者说它必然会和其他两个变量中的一个或者两个同时存在强相关性。因为从新车型设计的角度而言,下车身的变化一般都是被动调整以满足上车身的变化需求,如车型的换代升级增加了科技配置使底盘的布线布置和前后桥设计需要调整,又或者为了满足燃油经济性对原有发动机进行换代升级而对底盘进行设计变更用以匹配调教全新的动力总成配置等。不管是哪种情况,基本不会单独对下车身单独做设计变更,并且大部分整车厂会选择尽量不更改底盘设计。所以,实际上没有下车身变化独立产生的情况,也不会对投产时间造成真正的显著影响。
另一个问题变量是生产线节拍,节拍越高,则制造相同数量样件时所需的时间越少。虽然理论上这样的逻辑是成立的,但在工厂实际运营中有另外一个关键参数,即“产能利用率”。工厂生产线节拍提升的主要原因是产量的需求增加,节拍高的产线相比节拍低的产线每日的产量更大,根据“交付客户优先”的管理原则,大部分车企会优先实现量产交付,这也意味着可以被投产样车试制所利用的富余产能其实比低线速的工厂更少。与此同时,由于线速的加快对于操作工和一线管理的难度加大,需要更长的时间将产能爬坡至量产需求的稳定性(一般OEE85%以上、FTT90%以上),生产节拍在某些情况下与投产时间成正比关系。据此,该假设与原模型中成反比(系数为-0.78)不匹配。
6 结语
基于影响投产时间的关键因素建立数据库,采用多元线性回归模型并利用SPSS软件对投产时间影响因素进行多元线性回归分析。在得出方程系数的初步计算结果后对回归方程进行R方、显著性、变量共线性和残差分的检验,发现两个共线性较强的干扰变量。对变量进行删选并重新建模,得出的新方程解在自相关性和系数显著性上明显优于原方程,且更贴合正态分布的曲线。虽然可能由于样本数量不够的关系,依然存在少数变量的显著性不够,但是从统计学的角度,优化后的方程符合应用标准,故优化后的模型理论上可以成立。同时,结合实际的投产管理和生产制造经验对筛选出的干扰变量进行分析,解释其在现实案例里的实际意义。各个系数和解均满足多元线性回归方程的拟合度要求,并且大部分可以与实际案例相联系。为了使模型回归更准确,还需要进一步扩大样本搜集数量,并结合新智能制造的技术方案不断优化模型参数。
——与非适应性回归分析的比较

