跨中横隔板对箱形梁畸变效应影响研究

张元海，龙均翊，陈东亮，王晨光

(兰州交通大学 土木工程学院, 甘肃 兰州 730070)

随着箱壁厚度的日趋减小，箱形梁在偏心荷载作用下扭转时横截面变形即畸变不容忽视，由此产生的附加翘曲应力往往大于刚性扭转翘曲应力，而且畸变使箱板产生横向弯曲，因此，箱形梁的畸变效应分析受到许多学者的广泛关注。近年来，有些学者运用三维有限元数值模拟方法分析箱形梁的畸变效应，并分析了不同荷载形式、横隔板间距、高跨比、高宽比及板厚等参数变化对箱形梁畸变翘曲应力的影响[1-5]，其中，文献[1-2]对偏心荷载进行分解后，直接在有限元模型上施加分解后的畸变荷载，因而求得的应力即为畸变翘曲应力；文献[3-5]通过分别计算偏心荷载和相应对称荷载作用下的应力然后相减的途径，间接得出偏载作用下的翘曲应力，显然这样得到的应力包含了扭转翘曲应力与畸变翘曲应力，并未得出独立的畸变翘曲应力。除三维有限单元法外，一维梁段有限单元法也常被用于分析箱形梁的畸变效应及其他空间效应[6-8]，如，文献[6]建立的梁段单元可对箱形梁的弯曲、扭转、畸变及剪力滞效应等进行统一分析。虽然有限元数值解法特别是三维有限元法可用于任意边界条件下复杂箱梁的空间分析，但获得的变形、应力或内力不便于设计人员对结构的特定刚度进行判断或采取相应构造措施，而解析法却可以针对箱形梁的某种单一变形状态如畸变状态进行针对性分析，并直观反映各种影响因素，因此，解析法也被许多学者用于分析箱形梁畸变效应。王晨光等[9]基于广义坐标法原理，针对双轴对称矩形截面箱梁，用总势能变分法建立了畸变控制微分方程，并分析了剪切变形对畸变效应的影响；张元海等[10]在箱梁横截面的畸变中心处定义畸变角并建立控制微分方程，分析了顶板和底板两侧均设置外伸悬臂板的箱形梁畸变效应。近年来，波形钢腹板组合箱梁的畸变效应分析也受到关注。李运生等[11]用总势能变分法推导了波形钢腹板曲线箱梁的弯扭及畸变控制微分方程；文献[12-13]在分析箱梁各板元的面内和面外力系平衡条件的基础上，建立了波形钢腹板箱梁的畸变控制微分方程，分析了几何参数对畸变翘曲正应力的影响。然而，上述文献中的畸变效应解析法只能用于无跨内横隔板的箱梁。文献[14-15]提出了一种分析有跨内横隔板的箱形梁畸变效应解析法，可考虑横隔板的面内变形影响。部分学者对箱形梁畸变效应开展了试验研究[16-17]。

本文提出一种分析有跨内横隔板时箱梁的畸变效应解析法，首先解除跨内横隔板对畸变变形的约束作用，并代入相应的未知畸变矩，然后利用畸变变形协调关系求解未知畸变矩，继而在无跨内横隔板的初参数解基础上获得有跨内横隔板箱梁的畸变效应解析解，最后以承受均布畸变荷载的简支箱梁为例，分析跨中横隔板布置对箱形梁畸变效应的影响。

1 箱梁畸变变形描述

具有竖向对称轴的单室梯形箱梁横截面示意见图1。图1中，A、B、C、D分别为4个角点位置，b1、b2、b3分别为顶板、底板、悬臂板宽度，bw为腹板的斜高，h为梁高，θ为斜腹板的倾角，t1、t2、tw分别为顶板、底板及腹板的厚度。

图1 箱梁横截面示意

图2为箱梁横截面发生畸变变形后的示意图，角点A、B、C分别位移至A′、B′、C′。图2中，P为竖向反对称分布荷载，P1、P2、Pw分别为反对称荷载分解后作用于顶板、底板及腹板的分布畸变荷载。选取角点B处腹板与底板夹角的改变量γ作为畸变角，并以使∠ABC减小时为正。

图2 荷载及变形简图

由图2可以看出，截面畸变角γ由腹板的偏转角γ1和底板的偏转角γ2两部分组成，即

( 1 )

式中：uAB为角点A、B的相对水平位移；vBC为角点B、C的相对竖向位移。

若用f1、f2、fw分别表示箱梁顶板、底板及腹板在畸变荷载P1、P2、Pw作用下各自的面内位移，则有

uAB=f1+f2

( 2 )

图3为角点B、C处变位示意图，根据图3所示角点B、C处的变位关系，可得

( 3 )

将式( 2 )和式( 3 )代入式( 1 )，可得

( 4 )

图3 角点B、C处变位示意

2 畸变微分方程初参数解

根据总势能变分法[18]，可得箱梁的畸变控制微分方程为

( 5 )

根据总势能变分要求的边界条件可知，与畸变角γ及其一阶导数γ′(广义翘曲位移)相应的畸变内力分别为

Md=-EJdγ‴Bd=-EJdγ″

( 6 )

式中：Md为畸变矩；Bd为畸变双力矩。

令微分方程( 5 )中md=0，即先不考虑跨内畸变荷载作用，可得相应齐次微分方程的通解为

γ(z)=[C1sin(λz)+C2cos(λz)]sinh(λz)+

[C3sin(λz)+C4cos(λz)]cosh(λz)=

C4Φ1(λz)+(C2+C3)Φ2(λz)+2C1Φ3(λz)+

2(C3-C2)Φ4(λz)

( 7 )

式中：C1～C4为积分常数；Φ1(λz)～Φ4(λz)为克雷洛夫函数，即

Φ1(λz)=cos(λz)cosh(λz)

Φ2(λz)=0.5[sin(λz)cosh(λz)+cos(λz)sinh(λz)]

Φ3(λz)=0.5sin(λz)sinh(λz)

Φ4(λz)=0.25[sin(λz)cosh(λz)-cos(λz)sinh(λz)]

选取4个初参数为γ0、γ′0、Md0、Bd0，分别为箱梁起始端(z=0)的畸变角、畸变翘曲、畸变矩、畸变双力矩，由式( 6 )和式( 7 )建立各积分常数与各初参数之间的关系后，可将箱梁的畸变位移和内力通过初参数表达为

( 8 )

( 9 )

Bd(z)=4λ2EJdγ0Φ3(λz)+4λEJdγ′0Φ4(λz)+

(10)

Md(z)=4λ3EJdγ0Φ2(λz)+4λ2EJdγ′0Φ3(λz)-

4λBd0Φ4(λz)+Md0Φ1(λz)

(11)

当箱梁沿全跨承受均布畸变矩荷载md作用时，只需在式(8)～(11)的初参数解基础上按Md0所在项补充相应的荷载项，从而可得初参数解为

(12)

(13)

Bd(z)=4λ2EJdγ0Φ3(λz)+4λEJdγ′0Φ4(λz)+

(14)

Md(z)=4λ3EJdγ0Φ2(λz)+4λ2EJdγ′0Φ3(λz)-

(15)

式(12)～式(15)中，4个初参数可根据箱梁两端的边界条件确定。刚性固定端或梁端设置面内面外均为无限刚性的横隔板时，满足γ=γ′=0，即截面不变形且不产生翘曲位移；当梁端设置面内无限刚性但面外无限柔性的横隔板时，满足γ=γ″=0，即截面不变形且不产生翘曲正应力；当梁端不设置横隔板时，满足γ″=γ‴=0，即不产生翘曲正应力和剪应力。

3 跨内横隔板的处理

横隔板位置及其约束畸变矩简图见图4。图4中，跨内第1道和第i道横隔板所在截面的纵向坐标分别为z1和zi，任一计算截面的纵向坐标为z；若将跨内各道横隔板解除，其对畸变变形的约束作用可分别用相应的未知畸变矩L1、Li代替。

图4 横隔板位置及其约束畸变矩简图

根据初参数解，箱梁在畸变外荷载及未知畸变矩共同作用下的畸变位移和内力可表达为

(16)

(17)

Bd(z)=4λ2EJdγ0Φ3(λz)+4λEJdγ′0Φ4(λz)+

(18)

Md(z)=4λ3EJdγ0Φ2(λz)+4λ2EJdγ′0Φ3(λz)-

(19)

式中：n为计算截面至箱梁起始端之间的跨内横隔板总数。

根据跨内各道横隔板所在截面zj处畸变角为零的变形协调条件，可建立补充方程为

γ(zj)=0j=1, 2,…,N

(20)

式中：N为跨内横隔板总数。

根据箱梁两端4个边界条件及式(20)，即可求得4个初参数及N个未知畸变矩Lj(j=1, 2,…,N)。

4 畸变翘曲应力及横向弯矩计算

箱梁发生畸变时，除在其横截面上产生畸变翘曲正应力和剪应力外，由于组成闭合箱室的各板件还发生横向弯曲变形，故在各箱板内还产生横向弯矩。畸变横向弯矩可在沿箱梁纵向截取的单位长度梁段所形成的闭合框架上按结构力学方法进行计算，注意到横向弯矩关于横截面竖向对称轴呈反对称分布，且在各角点处有最大值，故只需计算角点A和B处的横向弯矩MA和MB，可利用畸变角γ表示为

MA=ψAγMB=ψBγ

(21)

式中：ψA、ψB分别为角点A、B处的畸变横向弯曲系数。

箱梁横截面上任一点的畸变翘曲正应力σd为

σd=-Eωdγ″

(22)

式中：ωd为畸变扇性坐标。

利用式( 6 )中畸变双力矩Bd的表达式，则式(22)可表示为

(23)

定义ξ为角点A和B处的翘曲正应力之比，即ξ=σdA/σdB，ξ可根据畸变翘曲正应力的自平衡条件确定，其大小只取决于横截面的几何尺寸。根据畸变翘曲正应力分布特征，只要求得角点B处的畸变翘曲正应力σdB，则箱梁全截面的翘曲正应力即可确定。角点B处的畸变扇性坐标ωdB为

(24)

为了计算畸变翘曲剪力流qd，需利用箱板微元体的平衡条件。箱板上任一点P处的微元体受力简图见图5。图5中，t为箱板厚度，s为沿板厚中心线度量的周边坐标，在箱梁正面上以逆时针方向为正。根据微元体的纵向平衡可得

(25)

图5 箱板微元体受力简图

将式(22)代入式(25)并对s积分，可得

qd=qd0+Eγ‴Sdω

(26)

利用畸变翘曲剪力流qd在箱梁横截面上不合成扭矩的条件，可求得qd0为

(27)

将式(27)代入式(26)，并利用式( 6 )中畸变矩Md的表达式，可得畸变翘曲剪力流qd计算式为

(28)

必须注意，式(28)中的积分应在箱梁全截面上进行计算，即对于带悬臂板的箱梁，积分区域包括闭口箱室和悬臂板。有些文献中只在闭口箱室范围内进行积分计算，这显然是错误的，只对无悬臂板的纯闭口截面箱梁才适用。

为便于实际应用，给出畸变翘曲惯性矩Jd和横向框架惯性矩JR的表达式为

b2t2+2bwtw(ξ2-ξ+1)]

(29)

(30)

式中：I1、I2、Iw分别为顶板、底板、腹板的横向单宽抗弯惯性矩。

5 数值算例分析

预应力混凝土简支箱梁计算跨径l为40 m,梁端和跨中均布置有横隔板，其厚度均为0.3 m，箱梁横截面尺寸见图6。箱梁采用C50混凝土，其弹性模量E为35 GPa，反对称竖向均布荷载10 kN/m作用于两侧腹板与顶板交接处，其方向与图2相同。

图6 箱梁横截面尺寸(单位：m)

按本文解析法和有限元软件Ansys中的壳单元Shell63分别对箱梁的畸变翘曲应力进行了计算，跨中截面和1/4跨截面角点A处的畸变翘曲正应力见表1。有限元计算时，全梁共离散为3 350个壳单元，3 378个节点；从反对称荷载中分解出各板件的畸变荷载后，以集中力方式施加在各相应节点上。由表1可以看出，本文解析解与Ansys有限元数值解总体上吻合良好。

表1 角点A处畸变翘曲正应力比较

为考察跨中布置横隔板后对箱梁畸变效应的影响，按本文解析法分别计算了有跨中横隔板和无跨中横隔板时箱梁的畸变效应，图7～图9分别绘出了畸变双力矩、畸变矩及角点A处横向弯矩沿跨度分布曲线。

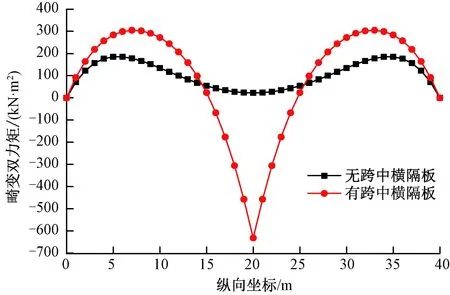
图7 畸变双力矩分布

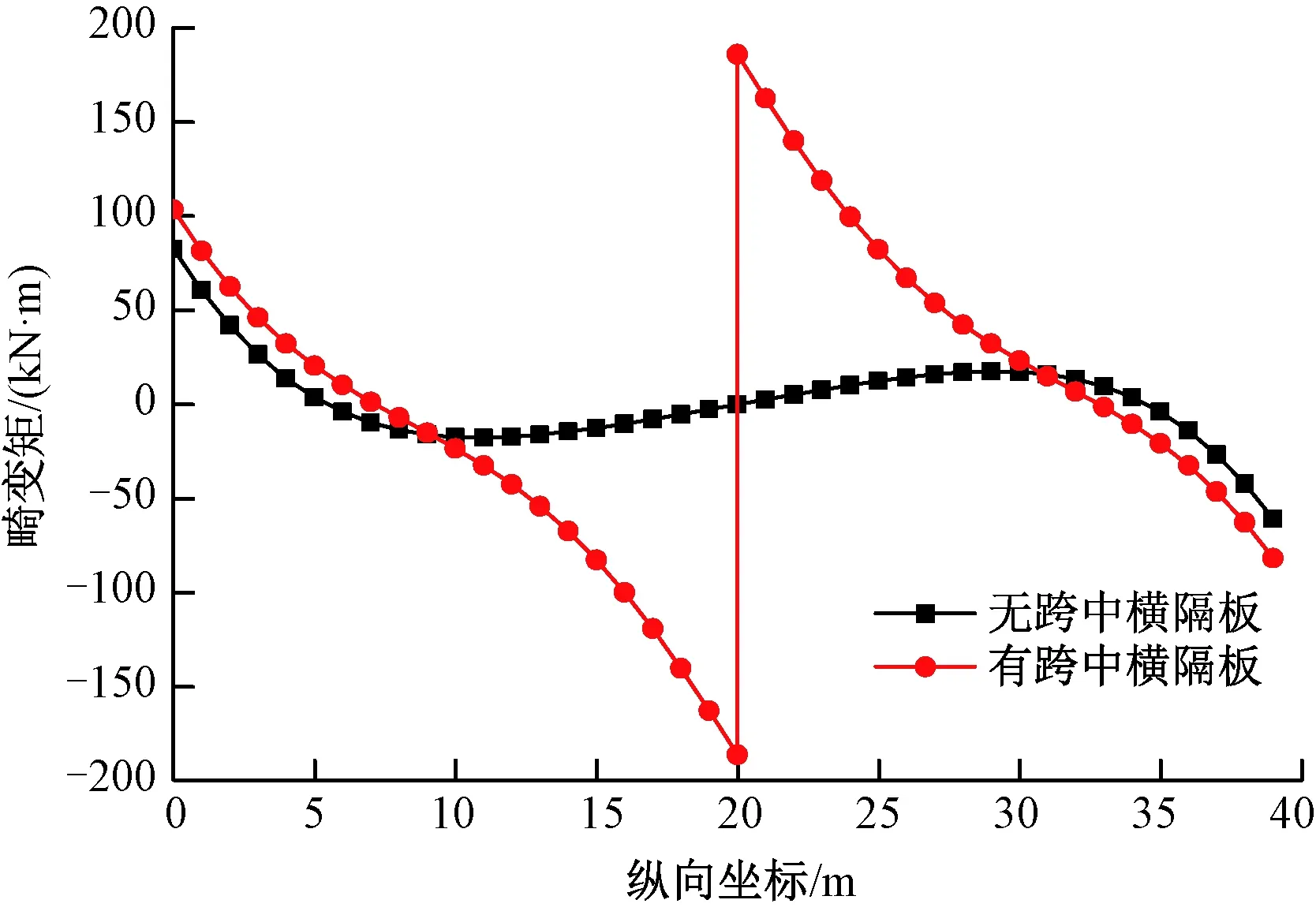
图8 畸变矩分布

图9 角点A处畸变横向弯矩分布

由图7～图9可以看出，在跨中截面布置横隔板后，虽然使跨中截面的畸变横向弯矩变为零，四分之一跨截面的横向弯矩也减小了34.4%，然而，跨中截面的畸变双力矩绝对值却增大了27.2倍(由22.39 kN·m2变为-631.23 kN·m2)，四分之一跨截面的畸变双力矩也增大了1.02倍，而且畸变矩内力也显著增大了(如跨中截面由零变为±185.98 kN·m)。可以看出，要通过设置跨中横隔板的方式减小畸变变形和畸变横向弯矩，必须以显著增加畸变双力矩和畸变矩从而显著增加畸变翘曲应力为代价。对预应力混凝土箱梁，畸变翘曲应力的显著增加必然会降低正截面和斜截面的抗裂性。进一步计算表明，与仅在跨中截面布置横隔板相比，若同时在1/4跨和3/4跨处也布置横隔板时，畸变内力分布才能得到明显改善。因此，在实际箱形梁的设计中，是否需要布置横隔板以及在哪些位置布置横隔板，必须根据具体情况决定。

跨中布置横隔板时箱梁跨中右截面的畸变翘曲剪应力分布见图10，图10中79.6 kPa为腹板上的畸变翘曲剪应力最大值，箭头表示剪应力方向。由图10可以看出，本例箱梁全截面最大剪应力发生在悬臂板根部，在底板中点及腹板内也存在较大的畸变翘曲剪应力。

图10 跨中右截面畸变翘曲剪应力分布(单位：kPa)

为了考察悬臂板宽度变化对畸变翘曲应力的影响，引入悬臂板相对宽度概念。定义悬臂板相对宽度κ为悬臂板宽度与顶板宽度之比，即κ=b3/b1，在维持顶板宽度b1不变的条件下，令悬臂板宽度从0增大至4.7 m，则相应κ从0增大至1.0，用本文解析法得到设置跨中横隔板的箱梁跨中截面角点A和角点B处畸变翘曲正应力随κ变化曲线见图11。由图11可以看出，随着悬臂板相对宽度的增大，角点A处畸变翘曲正应力迅速减小，而角点B处畸变翘曲正应力绝对值虽然逐渐增大，但其增大幅度很小。可见，角点A处畸变翘曲正应力对悬臂板宽度的变化很敏感。

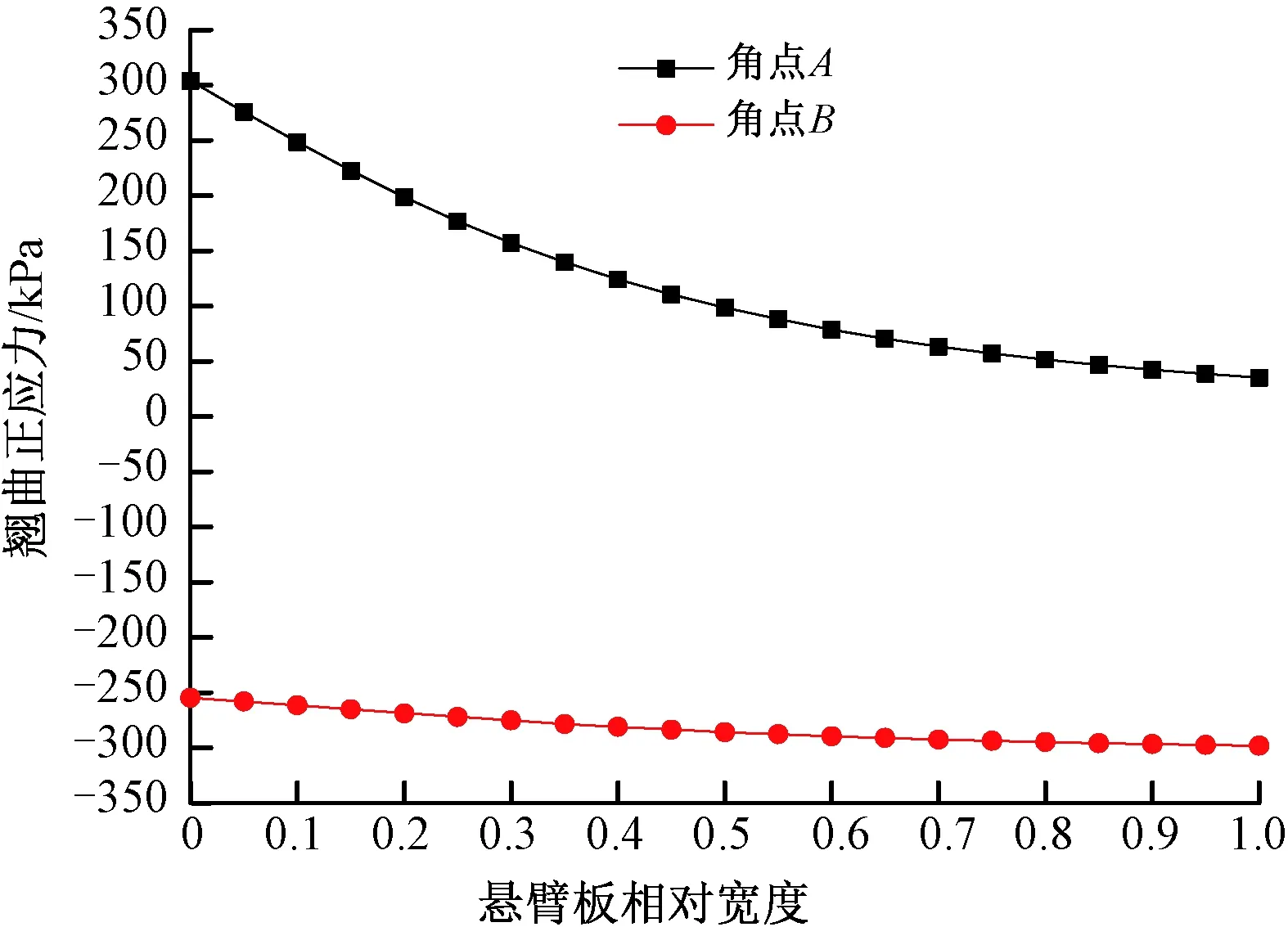
图11 畸变翘曲正应力随悬臂板相对宽度变化曲线

6 结论

(1) 本文提出了一种适用于跨内有横隔板箱梁的畸变效应解析法，将跨内横隔板用相应的约束畸变矩代替并根据变形协调关系确定其大小，从而在初参数解基础上获得有跨内横隔板的箱梁畸变效应解析解，通过Ansys有限元数值解验证了本文解析法的正确性。

(2) 布置跨中横隔板虽然可以减小箱梁的畸变变形及畸变横向弯矩，但同时显著改变了箱梁的畸变双力矩和畸变矩大小及其分布规律，从而使横截面内畸变翘曲应力显著增大，设计中应充分重视。

(3) 悬臂板宽度变化对顶板与腹板交接处的畸变翘曲应力有显著影响；随着悬臂板宽度的增大，顶板与腹板交接处的畸变翘曲应力迅速减小，而腹板与底板交接处的畸变翘曲应力变化很小。

(4) 算例箱梁的畸变翘曲剪应力最大值发生在悬臂板根部，在底板中心处及腹板内也有较大的畸变翘曲剪应力，在验算预应力混凝土箱梁斜截面抗裂性时应充分考虑畸变翘曲剪应力影响。