基于有限元法的挤压铝型材结构振动分析
秦德昭, 张天临, 余润洲, 张 勇
(1.上海电力大学, 上海 201306; 2.兰州兰石石油装备工程股份有限公司, 甘肃 兰州 730314)
铝合金型材应用十分广泛,在航天航空、工程建设、医疗器械、体育设施、家庭用具等各种领域扮演着重要角色。自1952年第一个铝合金车身应用于英国地铁以来,今天日本的高速列车全部由铝合金制成,欧洲国家铝合金车身制造技术也越来越好。与其他合金相比,铝合金具有高强度和轻质、耐腐蚀性和导热性好,以及制造工艺简单、整体制造成本低等优点。1958年,中国唐山机车车辆制造厂开发出中国第一辆铝合金乘用车[1]。1959年,铁道部四方机车厂通过铝和钢的混合铆接和焊接,成功实现了重量轻、重心低的生产目标。
目前,实现高速列车轻量化的最好材料是中空挤压铝型材,具有高比强度、高比刚度、耐腐蚀、较强设计性以及可再利用等优点。在速度超过200 km/h的高速列车上实现了全部铝化,其余轨道列车的用铝率也在逐渐增加,由此铝合金型材的需求随之迅速增长。
在结构分析中,铝合金结构的阻尼是重要参数之一,其阻尼性能对结构的分析结果有重大影响。结构的阻尼性能与结构本身所具有的结构特征,如振幅、自振周期、频率、耗能等参数有关[2]。因此,有必要对铝合金结构的振动进行分析和研究。针对铝合金结构的板式节点受力特性[3]、破坏机理[4-5]、节点刚度和承载力[6],国内外学者展开了相关研究并取得了诸多成果;针对铝合金板式节点网壳结构的静力承载性能的研究也趋于完善[7]。通过模态分析可以得到结构振型、固有频率、阻尼等参数,可为研究结构的振动特性[8]、分析产生故障的原因以及结构的动态优化设计提供依据[9]。
考虑到结构特性的不同,其振动特性也将有所不同。因此,本文结合结构模态分析,得到各阶自振频率和模态响应,并对所得数据进行了统计分析,得到了铝合金结构的固有频率;然后运用所得参数对结构有限元模型的动力响应进行了分析;最后,对铝合金不同结构件的振动特性进行了讨论。
1 3种结构的型材模拟分析
1.1 有限元模型的建立
本文以ANSYS软件为基础,对铝型材车体隔声特性进行研究,建立模型并进行仿真计算。ANSYS建立实体模型有两种途径[10]:一是利用ANSYS软件自带的建模功能创建仿真模型;二是使用ANSYS软件从其他软件导入构建的2D或3D实体模型。
本文通过ANSYS有限元软件建立铝型材车体的侧墙部分截面,采用1∶1比例建立,能更加真实地反映铝型材车体的隔声特性,避免因过度简化导致仿真结果误差过大。建模过程中的一些焊缝、圆角等忽略不计。采用由关键点连线,再由线生成面,最后拉伸得到体的建模方式。在有限元计算中,模型两侧的小矩形面受x,y,z自由度约束[11]。
此次建模规格为1 m×1 m×0.05 m的中空挤压铝型材。其框架结构如图1所示。为便于探究之后两侧板厚、肋板厚度、材料高度等因素对隔声特性的影响,初次建模只建立最简单的框架结构,未加肋板[12]。铝型材材料参数如下:型材结构密度为2.7×103kg/m3;弹性模量为700 GPa;泊松比为0.33;型材两侧轮廓厚度为5 mm;分析单元类型为Solid Brick20node 186[13]。

图1 型材框架结构
1.2 3种截面结构的对比分析
参考列车中常使用的肋板结构型材,铝合金型材的3种结构设计截面如图2所示,分别为矩形肋板、梯形肋板和三角形肋板。

图2 3种型材模型截面形状
本次研究采用Lanczos算法,用向量实现Lanczos递归计算。在模态分析完成且对模型施加必要的约束后,可以执行解算计算。不同肋板结构型材的10阶固有频率计算结果如表1所示。

表1 不同肋板结构型材的10阶固有频率
将不同肋板形状型材的各阶固有频率进行对比可知,原始框架第8阶模态之前的振型较规律,变形很小。从第8阶模态开始,振型在型材上出现较大变形,由此可推论在第8阶模态之前,型材结构的振动是整体性的;从第8阶开始,型材结构的振型开始呈现局部振动;第10阶虽然最大变形看似最小,但实际上对模态结构的整体破坏最大。此外,在各阶固有频率下,型材结构的危险点不仅影响铝型材结构的降噪特性,而且会影响其强度与安全性。矩形布置的肋板后型材结构的固有频率在第5阶到第6阶有一个大的飞跃,同时整体变形处于一个由局部变化大到整体变化大、再到整体变化小的过程;由第10阶整个模态结构位移可以看出,虽然整体最大变形变小了,但整个结构的危险区域大大增加。梯形布置的肋板与三角形布置的肋板在各阶固有频率上十分接近,型材的变形均随着阶数的增加处于一个先上升、再下降的波浪式趋势;危险变形区域也先随着阶数上升逐渐变小,最后再变大,与位移呈反比。将不同肋板结构型材的1阶和10阶振型进行比较,结果如图3和图4所示。
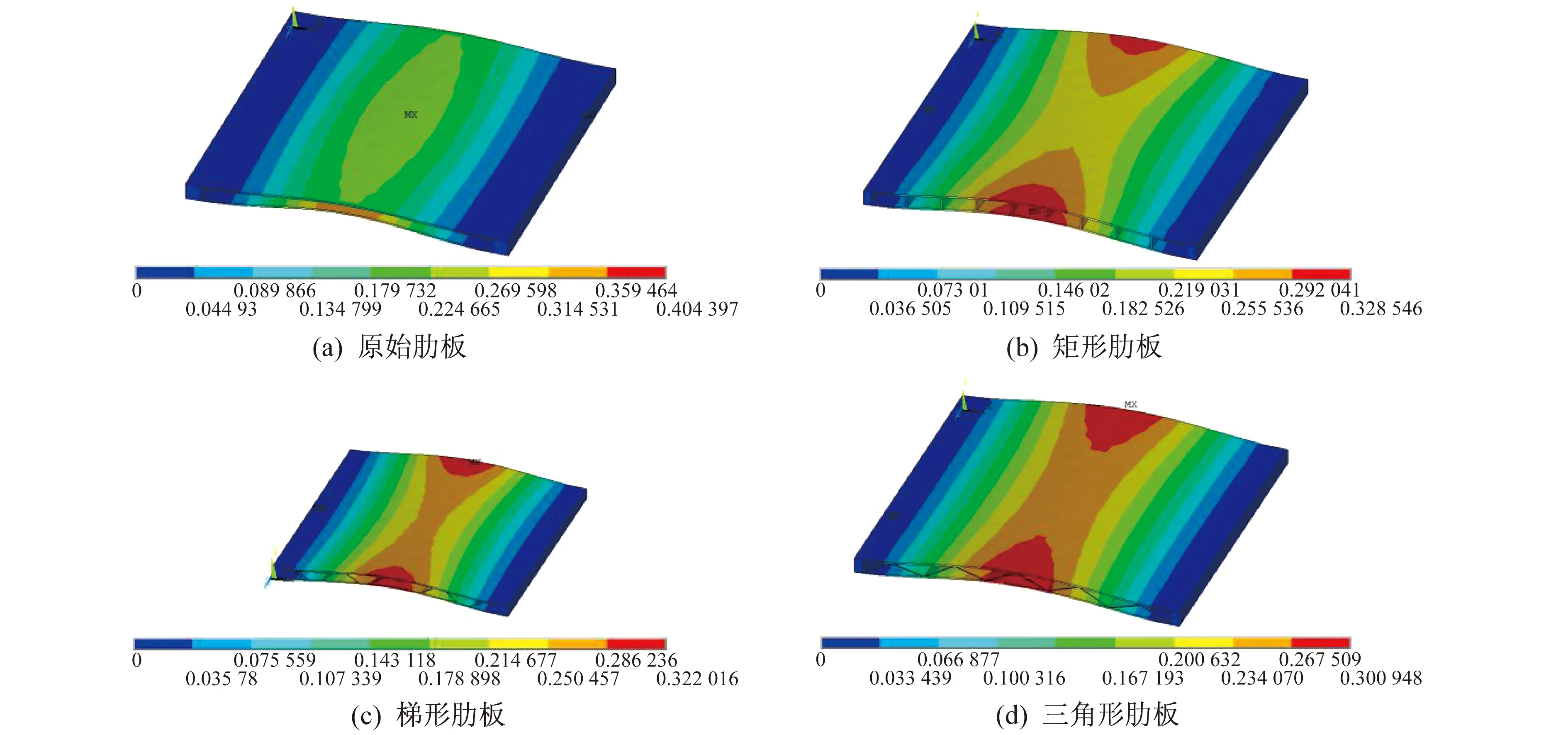
图3 不同肋板结构型材的1阶振型
由如图3和图4可以看出,1阶时,原始框架结构下板向上振幅较大,危险点处于下板中部,此时在型材下板中间,上下板一起变形,下板比上板变形更快。布置矩形肋板后型材结构的固有频率有所提高,同时整体变形处于一个由局部变化大到整体变化大,再到整体变化小的过程,型材中间外侧上下壁板一起变形。布置三角形肋板或矩形肋板后的各阶固有频率差距不大,但变形程度不同,布置矩形肋板后的变形是随阶数的增大而增大再减小,而布置三角形肋板后的变形是随阶数的增大一直增大。
无论是布置三角形肋板还是布置矩形肋板,整个型材的各阶危险区域在低阶很接近,但随着阶数的上升逐渐变得不同。在低阶时,三角形肋板布置方式变形更小;当阶数变高时,矩形肋板布置方式的变形更小。

图4 不同肋板结构型材的10阶振型
3种肋板布置方式的频率和变形情况比较,如表2所示。由表2可知:三角形肋板布置方式在其基频下变形最小,同时三角形肋板布置方式和梯形肋板布置方式比矩形肋板布置方式的基频频率更高;梯形布置虽然基频频率高于三角形布置,但是其变形比三角形更大;3种肋板布置方式的最大变形位置大体相同,说明即使是不同的型材结构,在一定固有频率下结构发生的振动是有规律的,模态结构的振型十分接近,只是变形的大小有所区别。综合来看,三角形肋板布置结构更加稳定与实用。在型材结构设计上,应根据实际情况选用三角形肋板布置方式。

表2 不同肋板布置方式比较
2 3种不同结构型材的振动特性分析
在10~450 Hz的频率范围内,以三相电磁振动台为激振源,对3种结构件提供加速度值为3g的简谐力激励。分别对3种结构件进行振动方向为水平(x向和y向)、垂直(z向),扫频速度为1个倍频的正弦振动。对同一载荷激励下、不同结构件的加速度响应函数进行测试,并进行下一步数据的处理和分析。
对于不同肋板布置的型材进行加速度(a)、位移(u)、频率(f)响应测试,取其最大值进行对比研究,结果表3所示。
由表3可知:加速度响应、位移变化、频率响应从矩形肋板、梯形肋板、三角形肋板依次减小,说明相同材料不同形状型材的肋板的振动情况为矩形肋板型材的振动响应大于梯形肋板和三角形肋板。

表3 不同型材最大加速度、位移和频率比较
3 结 论
对不加肋板的中空挤压铝型材结构进行了建模仿真计算,可以看出各项数据并不理想。然后对原始结构进行不同肋板优化布置,并对矩形肋板布置、梯形肋板布置、三角形肋板布置3种方式进行了设计建模和振动响应测试,计算了它们在相同材料属性、结构参数等条件下的各阶固有频率,探究了3种肋板布置方式对铝合金型材车体结构的影响,结论如下。
(1) 三角形肋板布置方式在其基频下变形最小,同时该方式和梯形肋板布置方式比矩形肋板布置方式的基频频率更高。梯形肋板布置方式虽然其基频频率高于三角形肋板布置方式,但在3种结构中其最大变形最小。
(2) 3种肋板布置方式的最大变形位置大体相同,说明即使是不同的型材结构,其在一定固有频率下结构发生的振动是有规律的,模态结构的振型十分接近,只是变形的大小有所区别。
(3) 型材系统结构的减振降噪特性的研究与其基频的关系更为紧密,综合来看,三角形肋板布置方式更加稳定与实用。因此,在型材结构设计上,应根据实际情况选用三角形肋板布置方式。

