“恒定电流”能否通过理想变压器*——对一道变压器调考题的深入研究

姜付锦 喻 聪

(武汉市黄陂区第一中学 湖北 武汉 430300)

黄亦斌

(江西师范大学物理与通信电子学院 江西 南昌 330022)

理想变压器是高中物理中一个非常重要的物理模型，它是从普通变压器抽象出来的，高中学段的学生对理想变压器的规律非常熟悉，但是对普通变压器的工作原理[1]，他们未必清楚，所以很有必要把理想变压器与普通变压器的区别与联系搞清楚.

1 普通变压器

首先假定两线圈(包括内部的铁芯)是线性元件(铁芯无磁滞、涡流等铁损)，于是可定义自感L1，L2和互感M.如图1所示，建立各物理量的正方向，其中副线圈中的电流i2的正方向可由要求M>0(i2在铁芯内产生的磁通方向与i1产生的一致)而确定.于是，根据法拉第电磁感应定律，两线圈的感生电动势(自感和互感之和)分别为

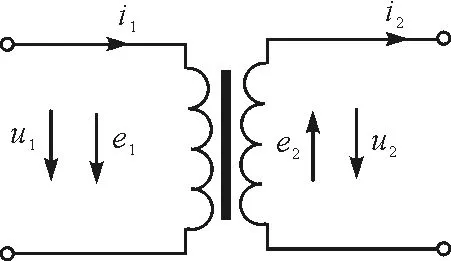
图1 变压器原理图

(1)

其中，磁通匝链数(磁链)Ψ1,Ψ2分别为

Ψ1=L1i1+Mi2Ψ2=L2i2+Mi1

(2)

线圈本身由金属导线制成，满足部分电路欧姆定律.设两线圈的内阻分别为R1和R2，则

u1=-e1+i1R1u2=e2-i2R2

(3)

若变压器无漏磁，此时每匝线圈的磁通量Φ都相等，故原、副线圈的磁链可以写成

Ψ1=N1ΦΨ2=N2Φ

(4)

无漏磁即是耦合达到最大，此时互感系数为[2，3]

(5)

将式(5)代入式(2)，可得

(6)

其中括号内的量平方的一半为

(7)

正是变压器的磁能，它正常情况下应该是有限大小.

联立式(4)和(7)得

(8)

在能量方面，联立式(1)～(3)得

(9)

式(9)表明：输入功率与输出功率之差提供了线圈内阻和介质中磁能的变化.如果线圈内阻为零且无漏磁，则由式(1)、(3)、(7)联立得

(10)

(11)

同时，式(9)可以变为

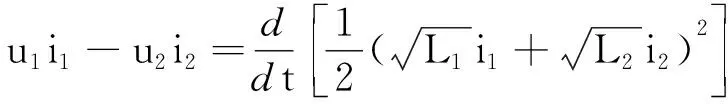
(12)

若已知u2(t)=i2(t)R，代入式(6)和(10)消去u2(t)和i2(t)得

(13)

若i1(t)已知，由式(13)可以求出u1(t)和u2(t).

2 理想变压器

若是理想变压器，则有

L1→∞L2→∞

(14)

则由式(13)得

(15)

再考虑到初始状态

(16)

再结合式(6)和(16)，输入电流和输出电流总成正比且反相，与具体变化情况无关，即

(17)

式(17)是瞬时关系，与具体的时间变化情况无关，有一段过程是常数时也照样成立.

3 一道调考题的分析

【调考题】一理想变压器的原、副线圈的匝数比为2∶1，在副线圈的回路中接有伏特表和阻值R=10 Ω的定值电阻，如图2(a)所示.原线圈一侧接在如图2(b)所示的交流电上，交流电的前半个周期为正弦交流电，后半个周期为恒定电流.伏特表的示数为

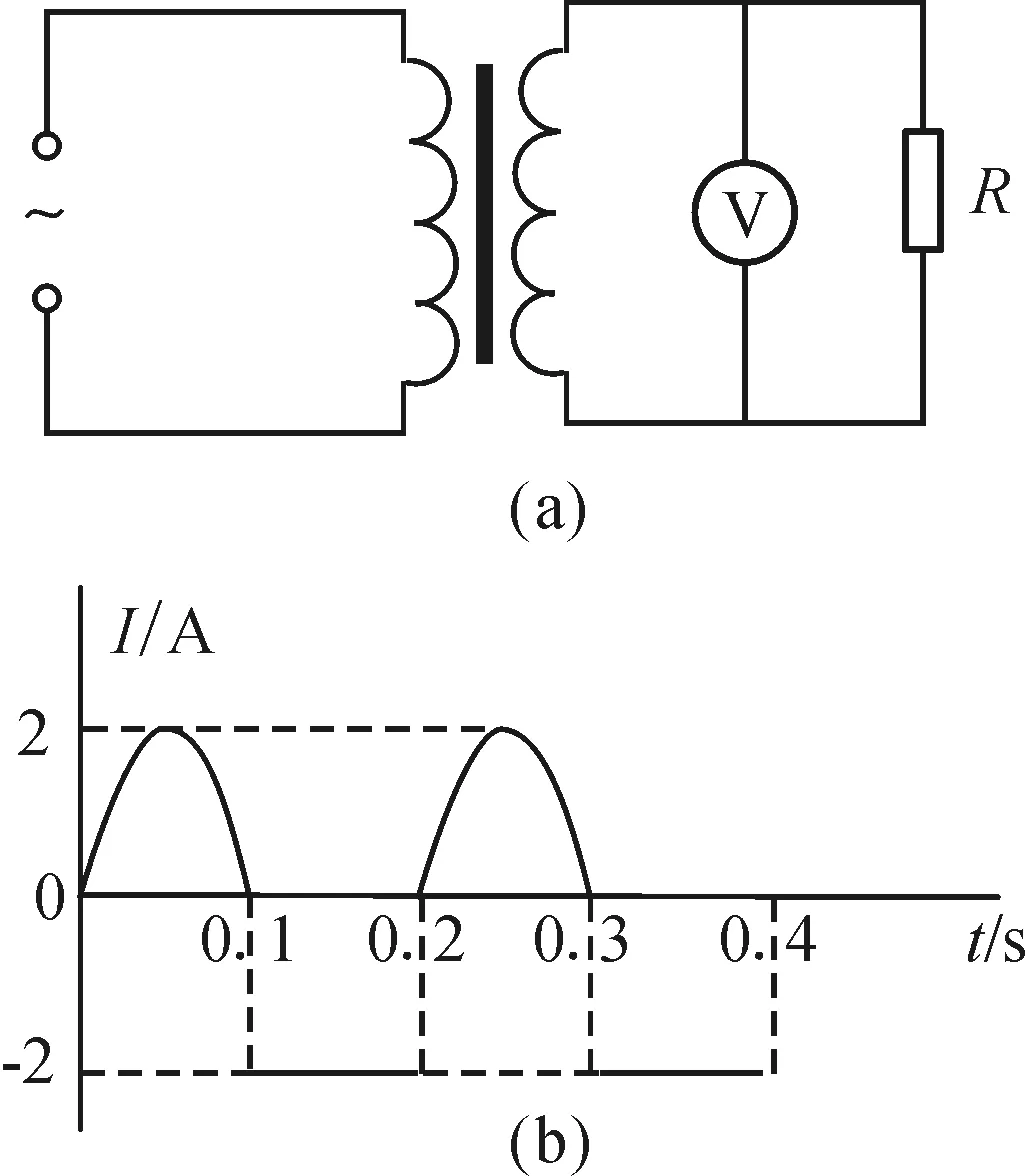
图2 调考题题图

3.1 参考答案

此题提供的参考答案为选项C，设原线圈中电流有效值为I1，由有效值定义得

(18)

解方程得

(19)

由电流比关系得

(20)

由欧姆定律得

U2=I2R

(21)

联立式(19)～(21)求得

(22)

所以，答案应该选C.

3.2 可能存在的4点疑惑

对以上调考题答案，很多教师认为是选项A.争议的焦点是图2(b)中负半周內变压器是否工作，毕竟直流电流是不能通过变压器的.

(1)输入电流为常数，就没有电磁感应吗？

错，别忘了互感，而我们并不清楚输出电流.只要副线圈中电流变化，那么原线圈和副线圈中都会有感应电动势，即使原线圈中电流为常数.

(2)输入电流和输出电流均为常数，就没有电磁感应吗？

这只是L趋近无穷时的结果，实际上，原线圈和副线圈都可以有(至少一边有)微弱变化，用电流变化率乘上无穷大的自感系数后，两边的电流和感应电动势就都不为零了.

(3)如果电流为常数的那段过程很长呢？比如一天的时间.

此条件与自感系数趋近于无穷大条件是相互矛盾的.具体情形依赖于到底谁更大.在正弦电流情形，这相当于问ωL是什么情况.过程很长，周期趋近于无穷大，ω→0.同时L→∞.那么ωL是什么情况？这需要重新定义，如果ωL→∞，那就说电流为常数的过程还不够长，L→∞为主要因素，变压器仍可视为理想变压器，上面的所有结论都成立，包括“直流变直流”(前提是整个周期中电流有变化的).如果ωL→0，那意味着L很大，但还不足够大，周期趋近于无穷是主要因素，前面理想变压器的结论不成立，需要重新考虑.(当然，考虑的结果就是无感应电动势)

(4)如果原线圈中电流一直是常数呢？

如果是这样的话，此时不能用L→∞，从而变压器不能认为是理想变压器.其处理方法是根据式(4)～(12)，式(12)在原线圈中电流一直为常数条件的解是变压器中磁场能是一个常数(初始条件包含在衰减项中)，于是从长时间来看，原线圈和副线圈中电压都为零，从而i2=0.

3.3 数学分析

一个非正弦周期函数，只要满足狄里赫利条件[4]，都可以展开为傅里叶三角级数.方波是一种非正弦曲线的波形，满足狄里赫利条件，可以展开为傅里叶三角级数

(23)

由方波的傅里叶三角级数展开可知:方波是由正弦基波和正弦奇次谐波的合成而成的.由此可知，变压器完全可以在方波情形下工作.还可以用傅里叶三角级数展开定量分析空载励磁电流：当输入电压为方波时，励磁电流是三角波，即磁通量变化是三角波，产生的感应电动势是方波.如图3所示，原线圈中的电压u1与空载电流i0有90°的相位差，电流表达式中分母的(2n+1)2是考虑到感抗与频率成正比，对i0求导后可以发现感应电动势正好是方波的傅里叶三角级数展开式.当副线圈接上负载后，输入电流的增量与输出电流在铁芯内的磁通量时刻抵消，不会影响输入电压方波的波形.

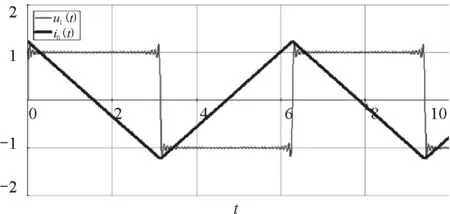
图3 方波电压和方波电压的励磁电流

4 数值模拟与仿真

4.1 接线图说明

如图4所示，仿真平台为Matlab2018a，在simulink中搭建电路图.因电流波形周期为0.2 s，故仿真时间设置为0.2 s，即可看出规律.区域1用于产生题中所示电流源，区域2是电流表，区域3是理想变压器，区域4是电阻，区域5是电压表.

图4 仿真电路图

4.2 仿真结果

仿真结果如图5和图6所示.

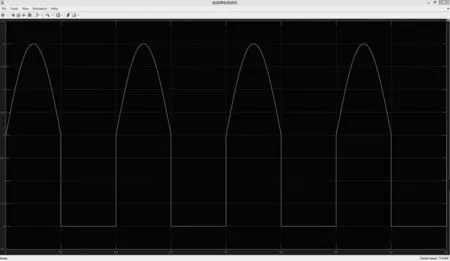
图5 电流源波形

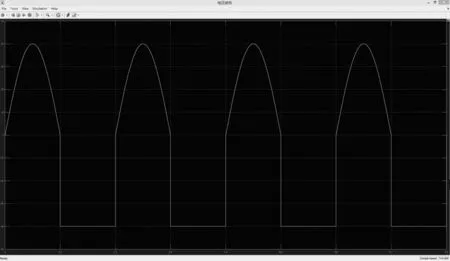
图6 电压表波形

可以看出，输入电流顺利地通过了理想变压器，电压表上的波形与输入端相同，所以输入电流中的“直流部分”可通过理想变压器.

4.3 补充说明

理想变压器中有一个参数magnetization resistance and inductance，该项设置为inf(无穷大)则表示理想变压器，但设置为inf后仿真失败，无法计算.于是改为1019，仿真才得以顺利进行.当设置为100或者1时(特性上比较接近于普通变压器)，电流通过普通变压器后有些失真.图7和图8为理想变压器设置参数与普通变压器的输出电压波形.

图7 理想变压器参数

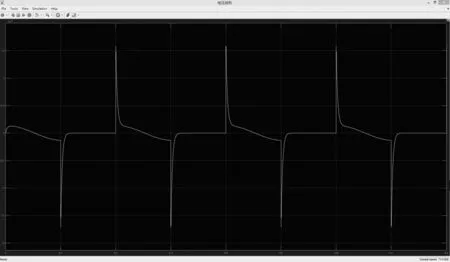
图8 普通变压器的输出电压波形

5 结束语

通过以上分析，不难发现：理想变压器是可以实现“直流变直流”(前提是整个周期中电流有变化)；变压器的原、副线圈存在互感现象，当L→∞时，原、副线圈中的电流只要有微弱变化，用电流变化率乘上无穷大自感系数后，原、副线圈的电流和感应电动势就都不为零了；当原线圈中的u1为方波信号时，u1与线圈中的空载电流i0有90°的相位差，对i0求导后，可以得出感应电动势正好是方波的傅里叶展开式，当副线圈接上负载后，输入电流的增量与输出电流在铁芯内的磁通量时刻抵消，不影响电压波形，故交变电流中的“直流部分”可以通过理想变压器.

致谢

本文中的数值模拟电路设计和仿真是由笔者的一个学生——李卓完成，他是华中科技大学光电与信息技术学院2017级研究生；在数学分析时也得到了重庆十一中学郎军老师的精心指点，在此特别感谢李卓和郎军老师对这个问题分析与解决所付出的努力.