基于距离置信度分数的多模态融合分类网络

郑德重， 杨媛媛， 黄浩哲, 谢 哲, 李文涛

(1. 中国科学院上海技术物理研究所 医学影像信息学实验室， 上海 200080； 2. 中国科学院大学，北京 100049； 3. 复旦大学附属肿瘤医院， 上海 200032)

在处理机器学习分类问题时，模型准确率的提高总是会被优先关注.较高的准确率固然很重要，但在有限样本的情况下，学习到的模型准确率可能很高，但模型的可靠性并不一定很高.在统计学中，置信度是度量系统可靠性的一个典型指标.置信度的重要性在于，如果一个决策支持系统对某个样本进行预测的信心太低，则可能需要人类专家参与决策过程.在实际应用中，置信度还具有识别未知类别样本的能力.因为当分类时，如果置信度较低，则表明要鉴别的样本与建立模型时用到的样本差异度较大.借助置信度能够扩大样本训练范围，通过再训练改善模型，提高模型的泛化能力[1-4].因此，良好的置信度应该是模型设计的一部分[1].在部署任何机器学习分类模型时，好的模型不仅要求有较高的准确率，而且还要能以较高的置信度进行正确分类.

机器学习中大多数生成的模型本质上都是概率模型，可以直接得到这样的置信度.但大多数判别模型无法直接获得每个类的预测概率，而是将相关的非概率分数作为一种替代，如支持向量机(SVM)分类器中的最大间隔[1,5-6].在评估一个神经网络模型的好坏时，通常会使用各种不同类型的分数来衡量模型的置信度.常用的方法是将最后一级输出单元通过Softmax软件归一化.此外，还可以利用输出单元的熵来计算，当预测某个样本的不确定性越低时，熵越小.虽然这些从输出端得到的分数与置信度相关，但使用这些分数度量置信度也存在一些缺陷，一些不可察觉的扰动可能改变神经网络的输出值.文献[7]通过实验在图像分类样本中加入噪声扰动，原本能够正确分类的样本在加入扰动后可以得到完全相反的预测结果，而加入噪声的图像在人的视觉观察中感觉不到任何变化.神经网络相比于人类在对数据的理解方面存在巨大差异，可能存在某些反直觉的情况“盲区”，也间接说明了神经网络可能存在某些人类难以觉察的不确定性，这种不确定将会直接影响输出结果和置信度[7-8].对于分类而言，将最后一级单元通过Softmax软件获得的概率最大值视为分类置信度是不准确的，因为这种方式忽略了与其余类预测概率间的关系，与真正的置信度之间有时存在着一定的偏差[3,9].既然从模型的外部计算出来的置信度不一定能够代表其真实的概率估计，那么可以尝试从模型内部入手.

为了获得一个对于神经网络分类模型可靠的置信度分数，许多研究者将注意力集中在神经网络的嵌入阶段，这些嵌入层被证明可以在许多相关任务中提供更好的语义表示[10-12].使用这种语义表示，通过估计嵌入空间中样本的局部密度来计算置信度分数，进而可以计算样本属于不同类别的概率.基于此，本文在嵌入空间提出一种基于距离置信度分数(DCS)的计算方法来度量模型的置信度.此方法不依赖于特定的分类模型，可以嵌入任何分类器中进行置信度计算.通过实验证明所提方法不仅可以用在单一模态分类模型中，还可对此进行扩展，将其用在多模态分类模型的置信度度量中.综上所述，本文的主要贡献如下：① 提出一种不依赖于特定分类模型的置信度度量方法，该方法不仅可以用在单模态分类问题，还可以用在多模态分类问题中；② 对于多模态分类问题，该方法可以量化评估单模态数据对于模型最终决策的影响，同时还可以知道不同模态信息对于最终决策时的重要程度差异.

1 研究理论

本文提出的基于距离置信度分数，主要借鉴以往两方面的研究：神经网络置信度分数和多模态融合研究.因此，下文将从这两个方面介绍相关工作.

1.1 置信度分数

Bayes模型在数学上提供了一种用来计算置信度的基础框架.文献[13-14]使用神经网络上的参数计算后验分布，用于估计预测不确定性来进行置信度的度量.文献[15]利用Bayes网络模型的拓扑结构结合多模态信息对非常规性突发事件的可能性进行量化评估.虽然利用Bayes方法来计算置信度的数学理论成熟，但在实际应用中实现起来相对困难，且计算成本高.文献[16]提出在模型测试时用dropout操作作为Bayes网络的一种简单替代，通过输出结果观察模型的不确定性.文献[17]提出使用对抗训练来改进网络基于熵分数的不确定性度量方法.模型置信度通常是从输出端的激活函数或其归一化中计算得到的，这些方法大多是通过对模型输出端进行外部观测，并将观测结果用于计算模型置信度.鉴于通过外部输出计算置信度有较多不足之处，希望能找到一种通过模型内部观测的方法，即找到一种能够代表真实概率估计的方法来计算置信度.

在度量学习研究领域中，如人脸识别、图像检索等，通过嵌入的方法可以学习从原始特征空间到一个低维稠密向量空间(嵌入空间)的映射，在该空间中样本的相似度可以通过距离进行度量.文献[18]在使用ImageNet数据集训练一个深层网络时，通过嵌入得到一个图像语义丰富的表示，并在此基础上进行分类.文献[10]基于深度嵌入的度量学习思想，在有限标记的成对样本之间进行相似性学习，完成不同图像的匹配任务.文献[11]通过提取图像特征学习高层次的嵌入语义来实现图像压缩.文献[1]还通过对抗性实验证明嵌入空间不仅含有丰富的语义信息，而且还具有一定的抗干扰能力.由此可知，通过嵌入方式可以将网络提取的特征从原来的特征空间映射到一个稠密的、可度量的嵌入空间中.在这个嵌入空间对样本进行局部概率密度估计，有望找到一种可以度量模型的置信度分数.

1.2 多模态信息融合

融合不同来源的信息主要有3种方式：早期融合、中期融合和后期融合.早期融合是在训练模型之前，将不同模态的特征串联起来，然后从串联特征中进行学习.中期融合首先是对各个单模态数据的特征进行一些初步学习，然后将学到的初级特征通过第2阶段融合加工进一步学习，最后将这些学习到的综合特征用于最终决策.中期融合方式目前大多是通过深度学习来实现的[19].后期融合方式是针对各种不同模态数据独立使用不同算法，然后根据任务特点使用一些技术组合方式进行最终决策.早期融合方式的主要优势是可以识别不同模态特征之间的关系，但该方式无法充分利用每种模态数据中自己的模式.早期融合只适用于相同类型数据间的融合，不同类型之间的数据不能直接融合，例如图像数据和文本数据.此外，早期融合方式着重于组合不同模态的特征，因此其通常具有很高的特征与样本比，容易导致分类时模型过拟合.后期融合方式与中期融合方法相比，后期融合方法实现更简单，但无法充分利用不同模态间的交互信息，只能通过每种模态信息独立判断后进行综合决策.中期融合方式目前在利用模式内信息和模式间交互信息方面具有一定的优势，并且可以充分利用深度学习强大的特征提取能力[20].本文提出的基于距离置信度分数来评估多模态分类模型置信度就是通过中间融合方式融合信息的.

2 计算方法

接下来，先介绍两种通常使用的从外部输出端得到的模型置信度分数.然后再介绍所提的从内部嵌入空间评估模型的置信度分数计算方法，最后介绍这种新的置信度分数在多模态分类模型中的构建.

2.1 输出端置信度分数

给定一个训练好的模型，通常使用以下两种分数来评估分类的置信度：基于最大距离置信度分数(MMCS)和基于熵置信度分数(ECS).文献[21]的实证研究表明，对外部输出而言，用这两种方法是相对有效的评估模型置信度的方法，文献[1]也曾用这两种分数评估模型的置信度.两种分数定义如下：① 基于最大距离的置信度分数.归一化后，网络输出层中的最大激活单元.② 基于熵的置信度分数.网络输出层中激活单元的(负)熵.

2.2 嵌入空间中基于距离的置信度分数

所提出的基于距离置信度分数的主要思路是借鉴度量学习方法，在网络特征提取后添加一层嵌入层，将原来网络中提取的特征进行映射，映射到一个语义丰富且可以度量的稠密空间中.在该嵌入空间中估计样本的局部密度，进而计算模型置信度，如图1所示.由图1可知，左侧特征提取部分用来提取样本特征；右侧两层全连接层，一个用于嵌入获得样本的向量表示，一个用于映射到输出以获取相应的预测值.

图1 基于距离置信度分数的计算示意图Fig.1 Schematic diagram of distance confidence score calculation

(1)

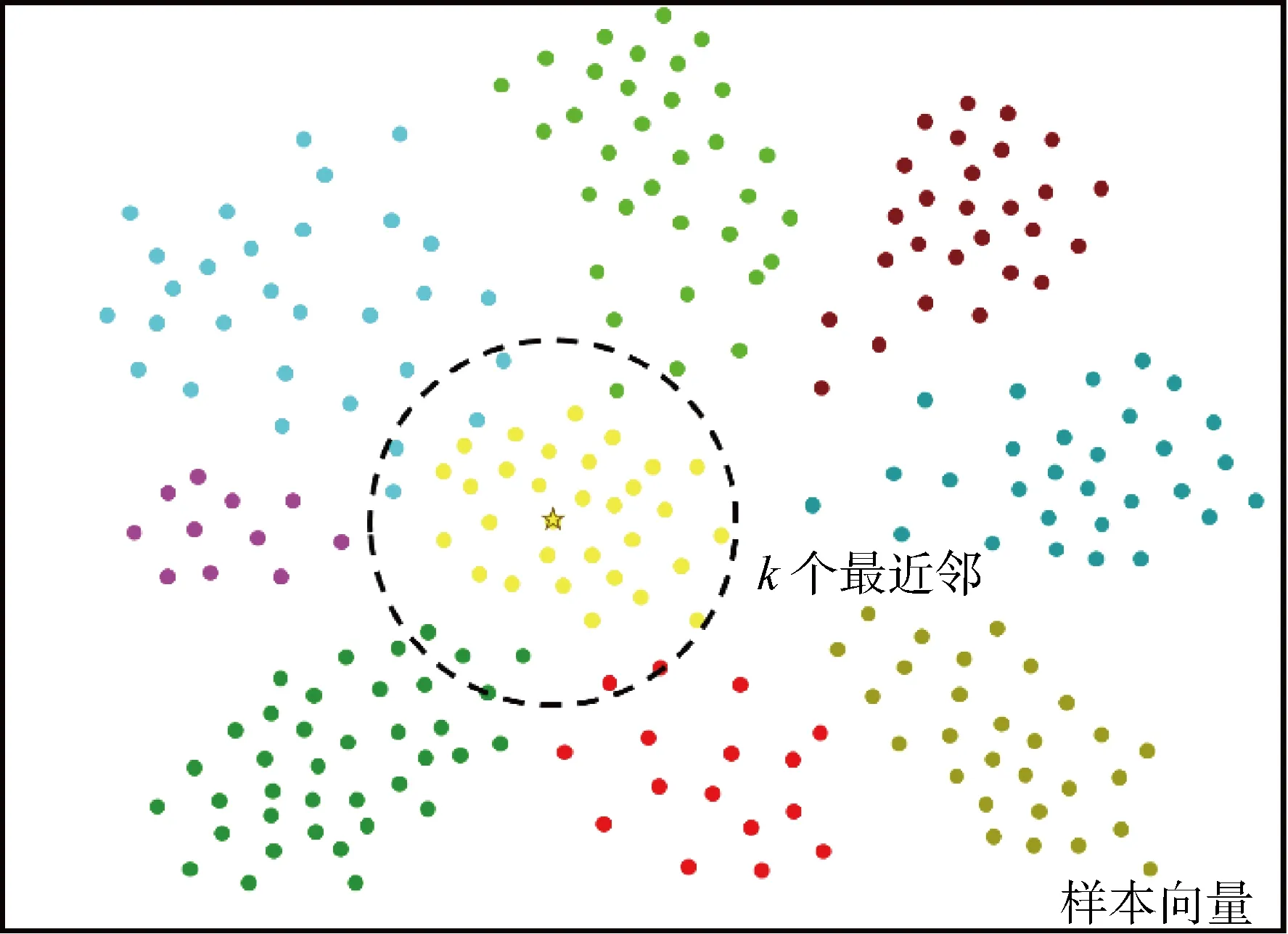
图2 最近k个点的密度估计Fig.2 Estimation of density of the nearest k points

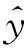
(2)

式中：max (·)为测试样本xi预测类别最大的分数，即最有可能的分类.

2.2.2利用中心损失提高嵌入效果 在度量学习应用中，鉴别的样本对象之间差异度相对较小，其分类模型要在能够对其进行细粒度鉴别的同时保持稳健性.早期主要是通过交叉熵损失来训练优化模型的，之后有学者提出了三重态损失训练模型，但在训练过程中三重态样本配对组合的差异度会影响模型的学习速度[22].文献[23]提出将中心损失用于面部识别，根据中心损失的梯度更新每个mini-batch中心，作为三重态损失的一种替代取得了良好的效果.文献[24]在少样本学习中使用了类似的方法，不断更新mini-batch的中心来进行优化，在场景识别任务中取得了不错的效果.中心损失优化时，最小化具有相同标签的样本到其样本中心之间的距离，将属于同一类的数据点聚集在一起，以获得在嵌入空间更好的向量表示[24].为了提高嵌入表达效果，使用中心损失来优化模型.中心损失可表示为

(3)

式中：Lso为交叉熵损失；Lcen为中心损失；f(xi)为第i个训练样本通过网络后得到的高维特征向量；hci∈RD为ci的样本中心，ci为xi的样本类别标签，xi∈RD，D为特征向量的维度；M为mini-batch的样本数量；λ为超参数.

2.3 距离置信度分数在多模态分类网络中的构建

图3 基于距离置信度分数的多模态分类网络构建示意图Fig.3 Schematic diagram of multimodal classification network construction based on distance confidence score

由上述可知，嵌入层添加在模型的特征提取模块之后，对于多模态分类模型可以使用相同的方法在各自模态特征提取后添加嵌入层用于计算置信度，如图3所示，其中：N为输入信息序号.在单一模态分类中由于信息源只有一个，不用考虑模式中特征重要程度的差异.但在多模态分类中，由不同信息来源间的模式提取到的特征重要程度存在差异，因此引入注意力机制.注意力机制最早在计算机视觉任务中提出，随后在自然语言处理领域也开始逐渐应用，随着BERT(Bidirectional Encoder Representation from Transformers)模型和GPT(Generative Pre-Training)模型在该领域中取得显著的效果，人们也越来越注意到注意力机制.注意力机制可以帮助模型将提取到的特征赋予不同权重，对关键、重要信息进行强化，帮助模型做出更加准确的判断[25-28].在多模态分类网络的特征提取阶段，为了强化不同模态提取自己的关键信息，在各自模态中做了注意力机制的处理.在提取图像特征时，使用了通道注意力和空间注意力机制[29]；在对文本类结构化信息提取时，使用了自注意力机制[27]；最后，在各自模态信息特征提取完成后再添加一个嵌入层，获取各自模态的高维向量表示，用来计算多模态分类任务中单一模态信息的置信度.在多模态分类网络的特征融合阶段，将各模态信息进行连接，并将连接后的所有信息再次嵌入，对多模态信息融合信息进行再次学习，其嵌入向量表示可以用来计算特征融合后的置信度.

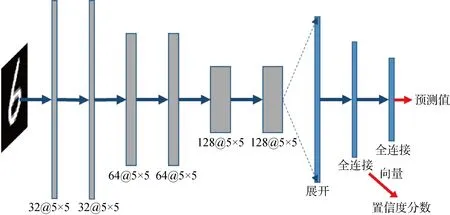
图4 MNIST分类网络Fig.4 MNIST classification network

3 实验和结果

在本节中，将通过3个实验任务来评估所提置信度分数.3个任务分别为：单模态分类任务MNIST数据分类、单模态分类任务CIFAR-10数据分类、多模态分类任务肺部腺癌数据分类.上述提到的需进行比较的3种置信度分数分别为：① 外部输出得到的基于最大距离的置信度分数；② 外部输出得到的基于熵的置信度分数；③ 所提出的通过内部嵌入得到的基于距离的置信度分数.

3.1 实验数据

(1) MNIST数据分类.手写数字数据集，该数据包含6×104个训练集示例，1×104个测试集示例，是美国国家标准与技术研究所(NIST)数据集合的子集.

(2) CIFAR-10数据分类.由10个类的6×104张32像素×32像素的彩色图像组成，每个类包含 6×103张图像，有5×104张训练图像和1×104张测试图像.

(3) 肺部腺癌数据分类.来自一家三甲医院采集的肺腺癌数据，包含 1 675 个样本，其中532例浸润性肺腺癌和 1 143 例非浸润性腺癌.每个样本数据有3种模态数据：高分辨计算机断层扫描(HRCT)图像数据、患者的结构化临床基本信息和血液检查信息.

3.2 实验设置

3.2.1MNIST单模态分类 该任务中，使用了一个由6层卷积层和2层全连接层构成的网络进行训练，如图4所示.其中：每个卷积层的卷积核参数用符号表示，如32@5×5表示32个5×5的卷积核.第1层全连接提取样本向量表示用于估计概率密度，进而计算所提出的DCS.第2层全连接输出用于计算MMCS和ECS.该实验分别使用了交叉熵损失与中心损失来进行优化比较.

3.2.2CIFAR-10单模态分类 对于CIFAR-10分类任务，使用了常规的ResNet50模型的特征提取器和2层全连接层构成的网络进行训练，如图5所示.其中：z为每个残差模块的输入；sg(g=1, 2, 3, 4)为残差模块;RelU为激活函数.模型首先提取图像特征，然后经过2层全连接，第1层将ResNet50模型提取特征进行嵌入，用来获取样本的向量表示，进而计算所提出的DCS.第2层全连接输出用于计算MMCS和ECS.该实验中，同样使用了交叉熵损失和中心损失来进行优化比较.

图5 CIFAR-10分类网络Fig.5 CIFAR-10 classification network

图6 基于注意力机制的图像特征提取Fig.6 Image feature extraction based on attention mechanism

3.2.3肺部腺癌多模态分类 肺部腺癌多模态数据包含1组图像数据和2组结构化文本数据.对多模态数据进行分类的网络由两部分组成：不同模态信息特征提取和多模态特征融合决策.

在特征提取部分，针对图像数据使用了添加注意力机制的ResNet50网络结构.在ResNet50网络结构的基本残差模块中，添加通道注意力和空间注意力两种注意力模块，用以提高图像重要部位的特征提取能力，如图6所示.其中：C为卷积核的通道数量；G为卷积核深度；H、W分别为卷积核的高和宽;ωch为通道注意力输出权重；ωsp为空间注意力输出权重；Sigmod为转换函数.对于另外两组结构化文本数据，使用了多层感知机提取特征，同时使用了自注意力模块来提高重要信息的提取能力，如图7所示.其中：ωse为自注意力输出权重；tanh为激活函数.

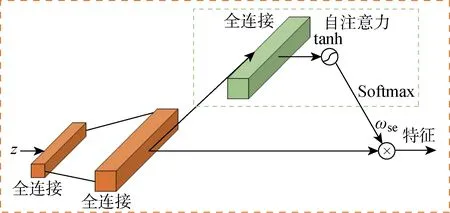
图7 基于注意力机制的结构化文本特征提取Fig.7 Structured text feature extraction based on attention mechanism

多模态特征融合决策部分如图8所示.首先, 将不同模态提取来的特征进行第1次嵌入，该嵌入空间的特征可以用来计算所提出的DCS，该分数可以反应不同模态信息的置信度.然后，将这些高维向量进行拼接并进行第2次嵌入，第2次嵌入空间的高维特征向量可以用来计算融合特征的DCS.最后，通过一层全连接进行输出，输出的向量用来计算MMCS和ECS.在该实验中，使用中心损失来对模型进行优化.

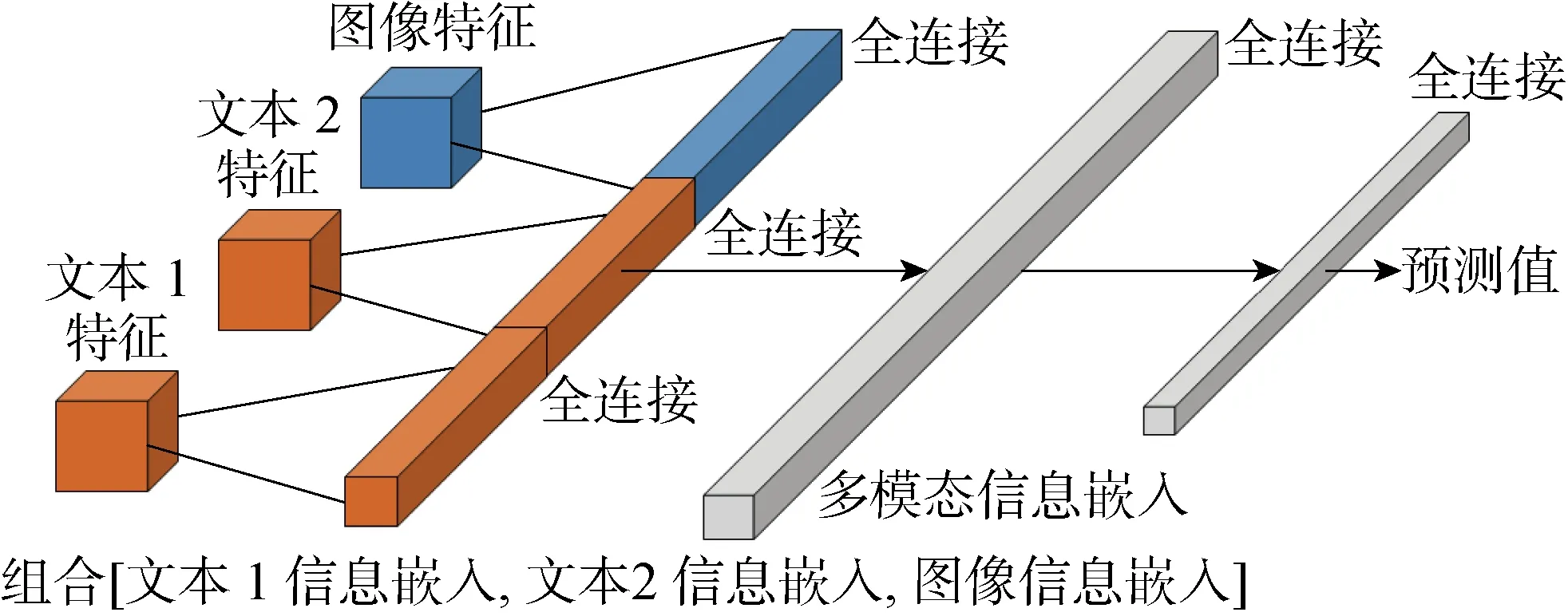
图8 多模态特征融合Fig.8 Multimodal feature fusion

3.3 评价指标

Brier分数(BS)是一种用来评估模型预测概率准确性的指标，是一种成本函数[30].Brier分数越低，其预测概率越准确，模型不确定性越低，置信度更高；反之，则置信度更低.Brier分数的取值范围为0～1.二分类Brier 分数的计算公式如下：

(4)

式中：Pi为预测概率；oi为二分类预测输出值，oi∈{0, 1}.对于多分类Brier 分数BSmut，其计算公式如下：

(5)

(6)

q=0, 1, …,Q-1

式中：Pij为多分类预测概率；oij为多分类预测输出值；Q为预测输出值可能的数量, 如10分类，则Q=10.

3.4 实验步骤

实验对每个模型进行30次训练迭代，计算每个训练迭代次数中的3种置信度分数：由外部输出计算的MMCS、ECS和由内部嵌入计算的DCS，观察其变化规律.在3个任务中选择训练出来的最佳模型，比较所获得模型的性能指标：准确率、接受者操作特征曲线下面积(AUC)、Brier分数.

由熵的定义可以知道，熵是预测结果不确定性的度量，不是预测每种可能性的度量分数，无法计算其Brier分数.基于熵的分数只用来观察其变化规律，不计算Brier分数，所以在实验中约定将外部输出得到的MMCS作为外部Brier分数(BSo)，将内部嵌入得到的DCS作为内部Brier分数(BSI).

图9 MNIST数据集上的模型准确率和AUC随E的变化曲线Fig.9 Model accuracy and AUC versus E on MNIST dataset

3.5 实验结果

3.5.1MNIST 模型训练中，准确率A、AUC随训练迭代次数(E)的变化规律，如图9所示.由图9可知，随着训练次数的增加，模型准确率和AUC逐步提高，最后趋于稳定，使用中心损失优化可以得到更高的准确率和AUC.3种置信度分数MMCS、ECS和DCS随E的变化曲线，如图10所示，其中：δ为置信度分数.由图10可知，随着E的增加，从输出端得到的MMCS和从内部得到的DCS都是逐渐增大后趋于稳定的，两者最后趋于相同，而ECS则是逐渐减小后趋于稳定的(见图10(a)).通过变化曲线的一阶差分可以知道，DCS和ECS正相关(见图10(b))，DCS与ECS负相关(见图10(c)).3种置信度分数间的相关系数如表1所示，其中：R为线性相关系数.

图10 MNIST数据集上3种置信度分数随E的变化曲线Fig.10 Three kinds of confidence scores versus E on MNIST dataset

表1 MNIST数据集上3种置信度分数间的相关系数

当训练稳定后，使用不同损失函数得到的最佳模型结果如表2所示.使用中心损失优化可以得到准确率和AUC，并且通过内部计算嵌入得到的Brier分数更低，反映出通过内部参数计算出来的置信度分数更加接近真实情况.

表2 MNIST数据集上由不同损失函数训练获得的模型性能

3.5.2CIFAR-10 模型训练中每个E的准确率、AUC随E的变化规律，如图11所示.由图11可知，随着E的增加, 模型准确率和AUC逐步提高，最后趋于稳定，使用中心损失优化可以得到更高的准确率和AUC.3种置信度分数随E的变化曲线如图12所示.由图12可知，随着E的增加，从输出端得到的MMCS和从内部得到的DCS都是逐渐增大最后趋于稳定， 最后两者趋于相同， 而ECS则是逐渐减小后趋于稳定的(见图12(a)).通过变化曲线的一阶差分可以知道，DCS和ECS正相关(见图12(b))，DCS与ECS负相关(见图12(c)).3种置信度分数间的相关系数如表3所示.

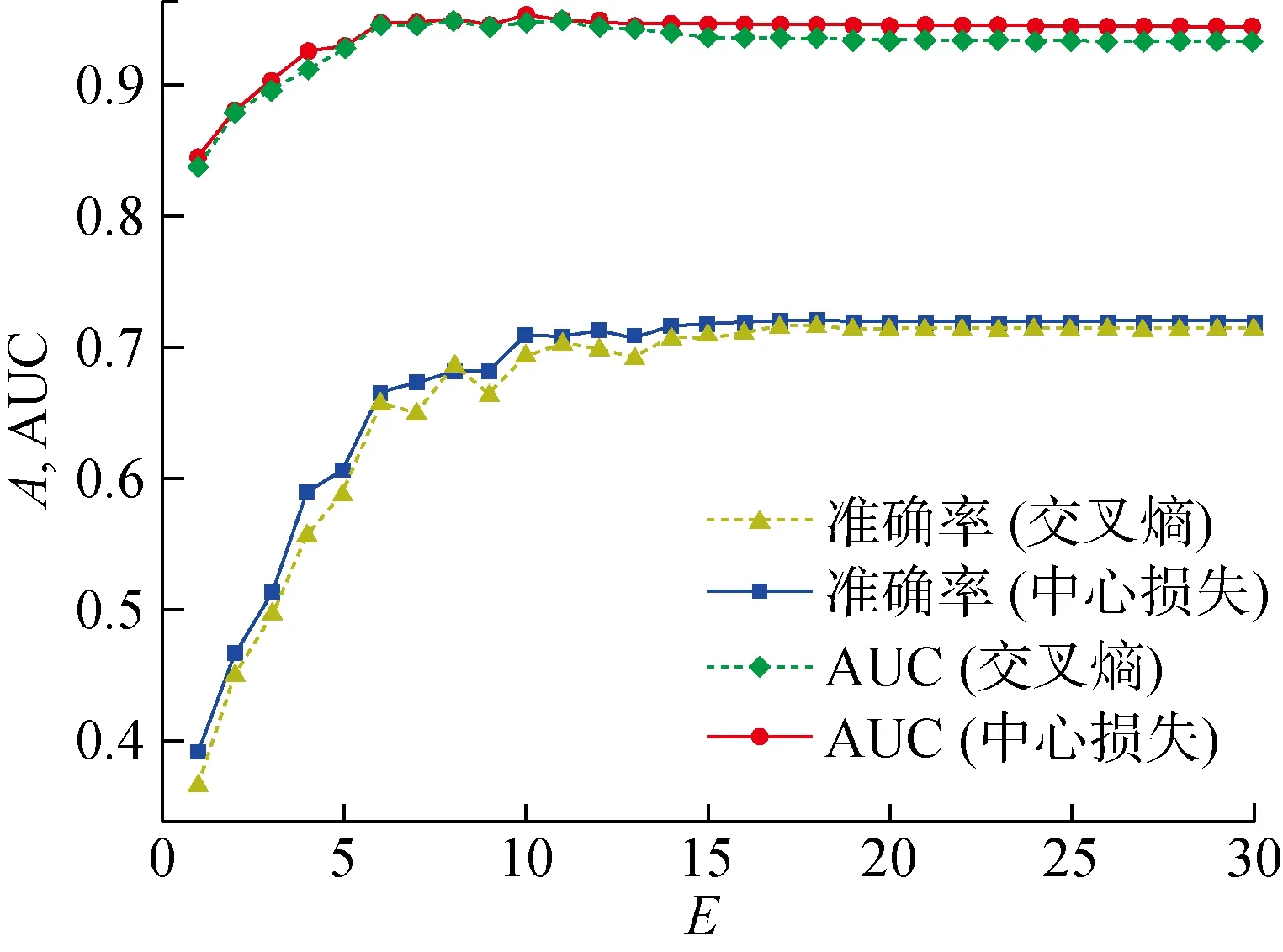
图11 CIFAR-10数据集上的模型准确率和AUC随E的变化曲线Fig.11 Model accuracy and AUC versus E on CIFAR-10 dataset

表3 CIFAR-10数据集上3种置信度分数间的相关系数

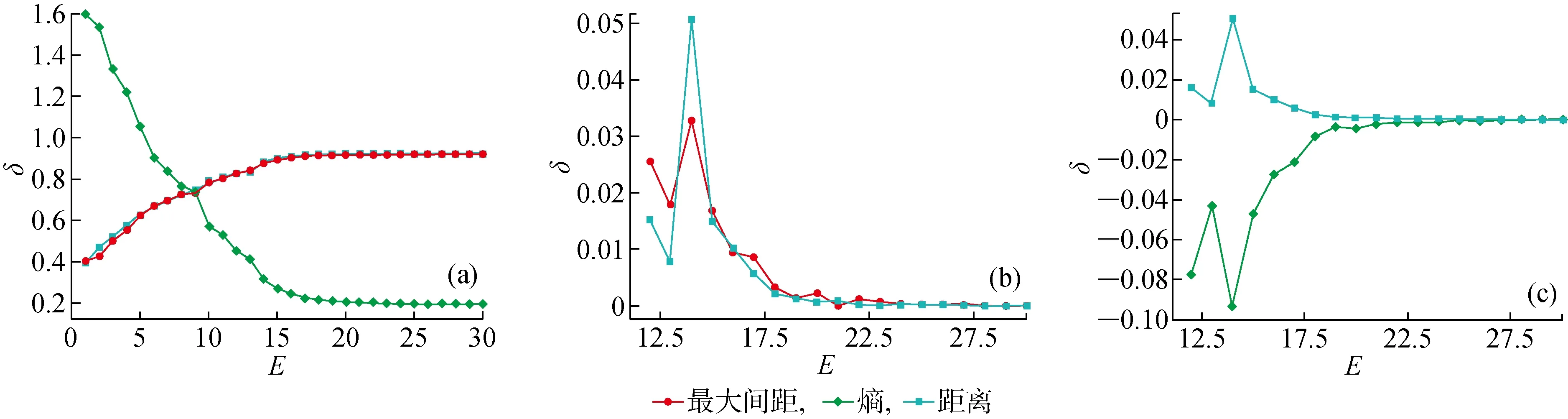
图12 CIFAR-10数据集上3种置信度分数随E的变化曲线Fig.12 Three kinds of confidence scores versus E on CIFAR-10 dataset

当训练过程稳定后，使用不同损失函数得到的最佳模型结果如表4所示.与MNIST类似，使用中心损失优化可以得到准确率和AUC，并且通过内部计算嵌入得到的Brier分数更低，反映出通过内部参数计算出来的置信度分数更加接近真实情况.

表4 CIFAR-10数据集上由不同损失函数训练得到的模型性能

3.5.3肺部腺癌 对于肺部腺癌多模态数据分类任务，不再对优化器方面进行比较，该任务全部都使用中心损失优化以获得更好的嵌入表示.训练中模型的准确率和AUC，如图13所示.由图13可知，随着E的增加，模型的准确率、AUC逐步提高，最后趋于稳定.当多模态数据加入后，相比于原来的单一模态图像数据，模型性能得到了提高.通过由输出端得到的MMCS、ECS和由内部嵌入得到的DCS随E的变化如图14所示.通过变化曲线的一阶差分可以知道，DCS和ECS正相关(见图14(b))，DCS与ECS负相关(见图14(c)).3种置信度分数间的相关系数如表5所示.

当训练稳定后，使用不同损失函数得到的最佳模型表现如表6所示.由表6可以看到，多模态数据可以增加模型分类的准确率、AUC，并且通过内部计算嵌入得到的Brier分数更低，反映出通过内部参数计算出来的置信度分数更加接近真实情况.

图13 肺部腺癌数据集上的模型准确率和AUC随E的变化曲线Fig.13 Model accuracy and AUC versus E on adenocarcinoma dataset

图14 肺部腺癌数据集上3种置信度分数随E的变化曲线Fig.14 Three kinds of confidence scores versus E on adenocarcinoma dataset

表5 肺部腺癌数据集上3种置信度分数间的相关系数

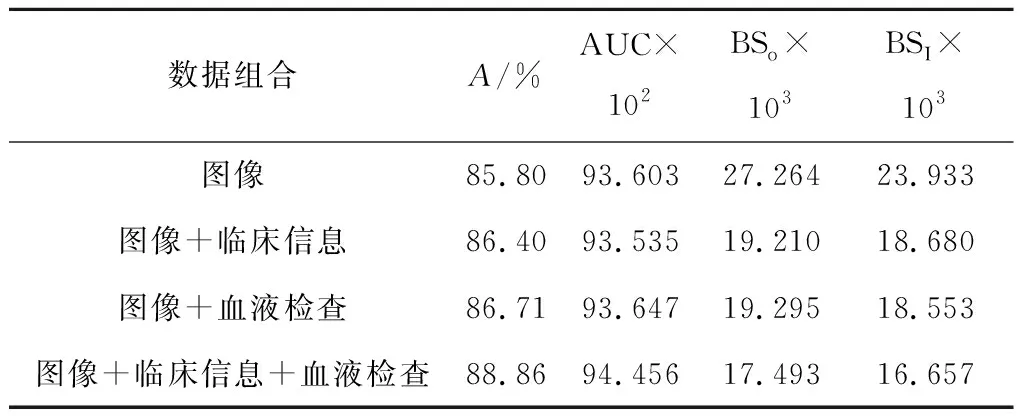
表6 肺部腺癌数据集上的多模态分类模型性能

表7 基于距离置信度分数的多模态数据Tab.7 Multimodal data based on distance confidence score

3.5.4结果分析 通过上述3组不同的实验数据可以知道，使用中心损失可以在获得更好的嵌入表示的同时提高模型的性能(准确率、AUC和置信度).另外，所提通过嵌入得到的基于距离的置信度分数与输出得到的基于最大距离的置信度分数和基于熵的置信度分数一样可以作为一种度量模型的置信度方法，且所提方法更能真实地反应概率预测情况.此外，相比两种由外部参数计算得到的置信度分数而言，在处理多模态数据分类时，所提出的基于距离的置信度分数不仅可以获得模型整体的置信度，还可以获得多模态数据基于自身信息在判断时的置信度，并可以量化不同模态信息的重要程度.

4 结语

本文提出一种在嵌入空间基于距离的置信度分数计算方法来度量模型的置信度.该方法在处理单一模态分类任务时，与其他通过模型输出端计算置信度分数方法相似，可以作为一种度量模型置信度的手段.在处理多模态融合分类任务时，不仅可以用来度量模型整体的置信度，还可以用来评估和量化多模态数据对于模型最后判断时的置信度影响，知道各种模态数据对于决策的重要程度.这一点在实际应用中对模型可靠性和可解释性都有要求的场合中具有重要意义.