风力机翼型非定常流场POD和EPOD分析

孙 翀， 田 甜， 竺晓程， 杜朝辉

(上海交通大学 机械与动力工程学院， 上海 200240)

风能是当前最具大规模开发价值的可再生能源之一，风力机作为风能利用的主要装置，在向大功率发展的同时，其产生的噪声对人们生活的影响也日益明显，降噪已经成为风力机研究的重要方面[1-2].二维翼型作为风力机叶片最基本单元，其非定常流场对风力机整机性能以及气动噪声水平具有重要的影响[3].在气动噪声方面，有研究表明由翼型绕流产生的气动噪声包括：尾缘噪声、钝尾噪声和失速噪声[4].其中，现代大型水平轴风力机气动噪声又以涡团通过叶片尾缘后形成的尾缘噪声为主[5].为此，需对翼型的非定常流动进行精细的求解和分析.

实验测试和计算流体力学(CFD)是研究翼型非定常流动的主要方法.其中，CFD方法拥有花费低，限制少等优势，因此被广泛运用于翼型流场数据的获取.但是，由CFD得到的非定常流场数据非常庞大，直接对其主要流动结构分析较为困难.降阶模型方法通过一组低维变量构成的特征模态来表示非定常流场.其中，本征正交分解(POD)方法是模态分析方法中较为传统和常用的一种方法，通过POD方法可以提取获得非定常流场的主要流动模态，其特征值直接表征对应模态的能量[6].在翼型非定常流动的POD应用方面，董圣华等[7]研究了超临界翼型在跨声速抖振下的非定常流场，采用POD方法提取了导致抖振的主要流动模态.Zhao等[8]使用POD方法研究了凹凸前缘翼型流动控制机理和气动特性.

对于流场中某个特定的区域或者某些观测变量的研究，若其能量占流动总能量的比例较小时，POD方法会有一定的局限性， Borée[9]提出了扩展本征正交分解(EPOD)方法，可以获得与某个区域中与观测变量最相关的流动结构.Schlegel等[10]基于EPOD方法，研究了射流中于气动噪声最相关的流动结构.

本文通过大涡模拟(LES)方法，数值计算风力机S809翼型在不同攻角下的非定常流场，并求解Ffowcs Williams-Hawkings(FW-H)方程获得远场翼型远场气动噪声.通过POD方法对流场数据进行降阶处理，获得主要的非定常流动结构，并进一步通过EPOD方法，构建远场气动噪声与翼型非定常流动的关系，提取与气动噪声最相关的流动结构，揭示风力机翼型气动噪声形成和传播的物理机制，为大型风力机降噪提供理论依据.

1 数值计算

对典型风力机S809翼型进行数值计算，翼型弦长c=0.2 m，计算域原点为翼型气动中心(1/4弦长位置)，半径为20c，展向长度为c.使用ICEM (The Integrated Computer Engineering and Manufacturing)软件对计算域做结构化网格划分，周向288个节点，径向215个节点，展向41个节点，总网格数达到250万，全局网格如图1所示.为提升壁面边界层内的计算精度，对翼型附近网格进行加密，近壁面第1层网格高度设置为0.005 mm，该值保证了壁面无量纲距离y+小于1，并将网格壁法向膨胀比设置为1.1以实现边界层计算高分辨率.

计算边界条件参考文献[11-12]，如图2所示.进出口设置于翼型前后20c处，进口给定来流速度v0=38.63 m/s，出口背压设置为一个大气压，由于风力机翼型来流马赫数低，计算域足够大，该边界设置与远场条件非常接近；展向边界设置为对称面；翼型表面设置为无滑移壁面.使用商业软件ANSYS CFX进行数值计算，湍流模拟使用LES Wale模型.计算时间步长设置为dτ=0.02 ms，使计算平均库朗数在1左右，以保证对湍流发展的数值模拟精度.

图1 翼型计算网格Fig.1 Computation mesh of airfoil

图2 计算域边界Fig.2 Computation domain

2 POD及EPOD方法

(1)

j=1,2,…,n

式中：φj(ξ)为第j个空间模态；aj(t)为第j个时间系数.POD方法则是为这样的分解形式寻找一组正交的模态[13].为寻找这样的一组正交模态，可以采用快照方法.首先，定义离散时刻下的流场快照zi∈Rm×1，m为流动变量q的空间维数，则有：

(2)

i=1,2,…,n

式中：ti为研究时间t内的离散时刻.将这些快照组成快照矩阵：

(3)

求解快照矩阵协矩阵的特征值问题：

ZTZΨj=λjΨj

(4)

j=1,2,…,n

式中：ψj为第j个特征向量；λj为第j个特征值.该特征值λj即为流动变量q的POD特征值λqj，而q的POD特征模态φPOD,j由特征向量ψj的变换获得：

(5)

j=1,2,…,n

动能可以通过POD特征值之和来表征，每个模态能量占总能量的比重可以由对应特征值与特征值之和的比值表示.因此，将特征值从大到小排列，所对应的前几阶POD模态便为表征流场波动的主要模态.

根据式(1)，通过POD特征模态φPOD,j的原始快照zi为

(6)

i=1,2,…,n

式中：βqi,j为模态系数.

通过求解式(6)可获得模态系数矩阵：

(7)

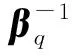
(8)

若有另一个时空域Ω上的流动参数l，则EPOD研究了l对q的模态投影的关系.为获得EPOD模态，首先对参数q做POD分解，可以得到参数l的POD特征值λl，以及参数l的POD模态系数βl,则q关于l的EPOD模态φEP满足如下关系[9]：

(9)

EPOD模态被证明为表示q中所有与l相关的流动结构[9]，由模态特征值λl的大小排序，可以得到与l最相关的流动结构.

3 计算结果

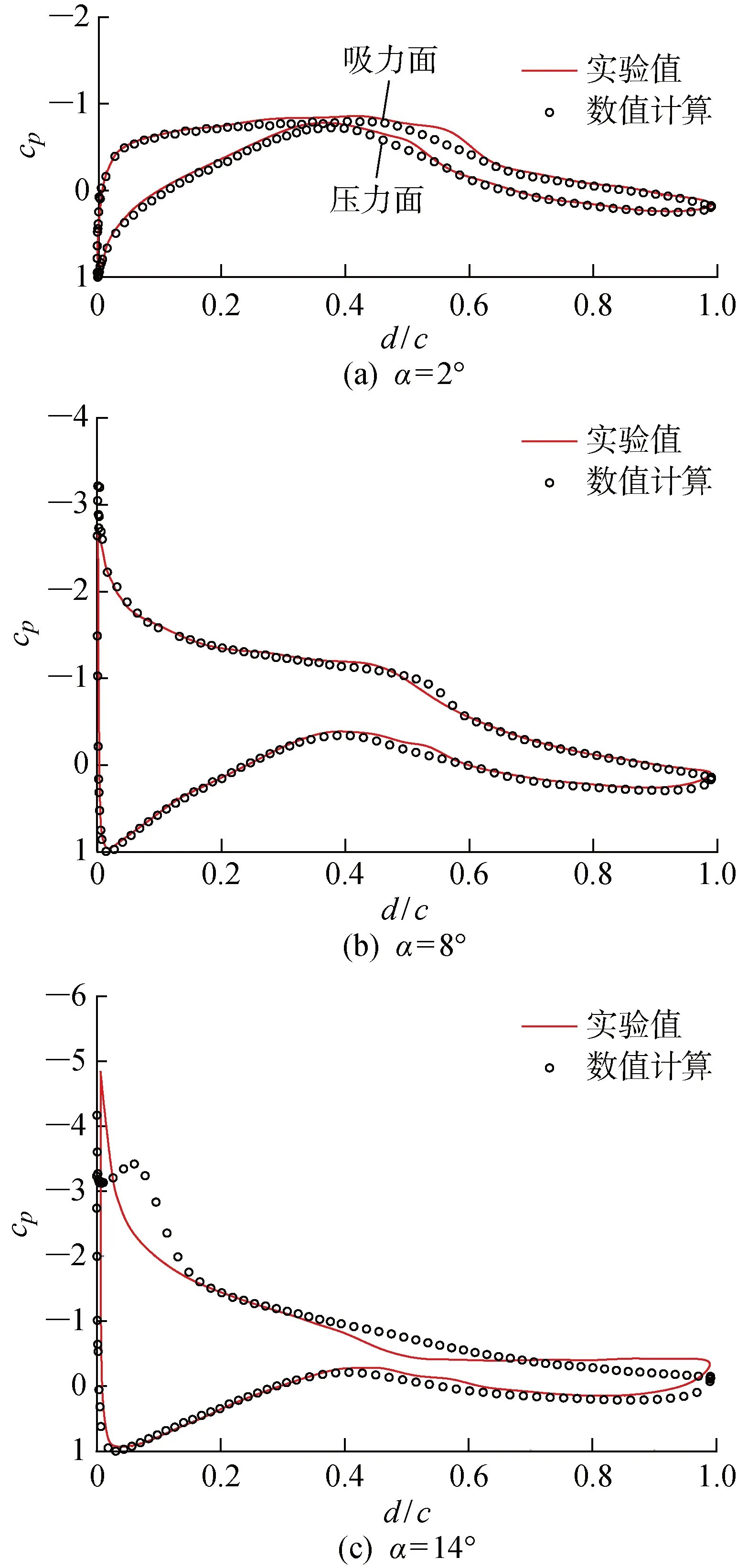
图3 翼型表面压力系数Fig.3 Pressure coefficients of airfoil surface

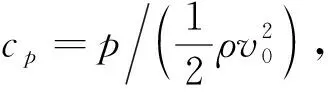
根据以上数值计算结果，通过求解FW-H方程，可以获得声压监测点下的翼型气动噪声.当翼型攻角为8° 时，气动中心正上方2 m位置处的监测点声压频谱如图4(a)所示.其中：f为频率；SPL为声压级.气动噪声呈宽频凸起特性，驼峰对应频率在500～800 Hz范围，整体变化规律与NREL的BPM(Brooks, Pope, Marcolin)翼型自噪声预测模型结果接近.

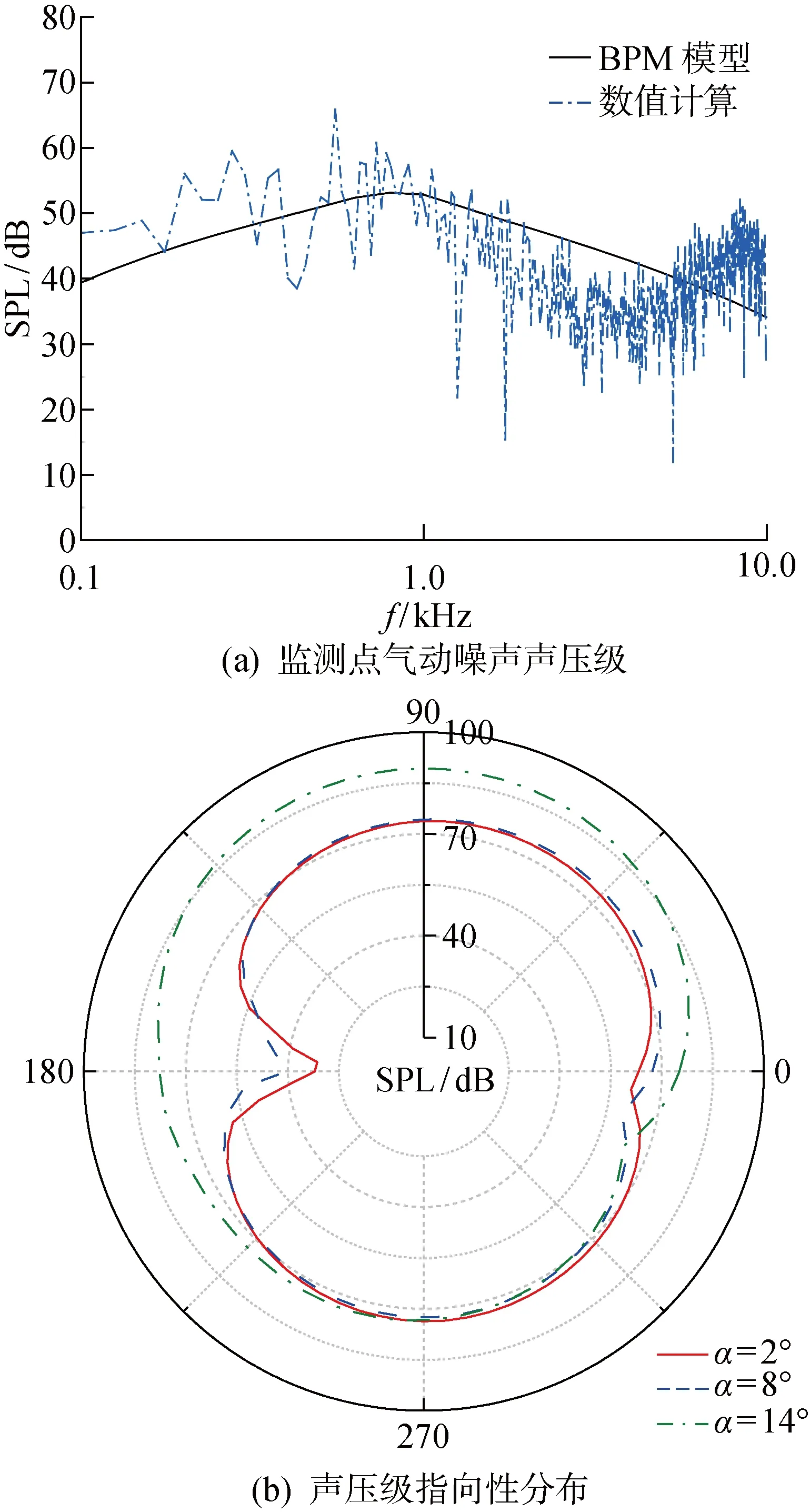
图4 翼型气动噪声Fig.4 Aerodynamic noise of airfoil

为研究翼型气动噪声指向性，需要计算不同传播方向上的气动噪声强度，翼型气动中心为圆点，以10c(即2 m)为半径，圆心角每隔5° 布置一个声压监测点，共72个监测点。计算这些监测点上的时均总声压级，获得的不同攻角下翼型气动噪声声压级指向性分布如图4(b)所示.由图4(b)可知，当翼型攻角为2° 和8° 时，气动噪声强度在翼型上下对称，而在翼型前后明显衰减，具有偶极子特征.翼型前部气动噪声强度明显弱于尾部，但随着攻角的升高，翼型前部气动噪声逐渐增强.进一步比较可以发现，翼型在攻角由8° 上升至14° 后，翼型吸力面侧噪声显著增强，而压力面侧噪声强度变化不大.

4 流场POD和EPOD分析

根据翼型在8°攻角下的非定常流场，每隔10步提取一个涡量流场数据作为一个快照样本(快照间隔为2×10-4s )，共550个快照构成快照矩阵Z，并做POD分解，获得的POD特征值λ如图5所示，其中：N为模态序号.由图5可知，POD特征值大小迅速下降，前4阶POD模态占流场波动总能量的45%，前40阶模态占总能量的90%.

图5 POD特征值Fig.5 Eigenvalues of POD

因此，POD方法可以有效地降阶高维非定常流场.分解得到的POD前4阶模态及其对应模态时间系数的频谱分布如图6所示.其中：x，y为翼型平面几何坐标；A为振幅.从图6中可以看到，第1阶模态结构主要出现在尾缘位置.因此，翼型涡量流场最主要的非定常结构表现为翼型附近尤其是尾缘处的涡团，其模态系数的频谱呈宽频特征，且主要集中在中低频(小于1 kHz).第2、3阶模态结构从前缘开始，主要表现在翼型中部位置，该位置接近转捩位置.在转捩位置之前， 层流流动附着壁面，随着逆压梯度逐渐增强，流动开始失稳，层流边界层脱离壁面，随后湍流边界层再次附着，在翼型壁面上形成层流分离泡，并在此处发生流动转捩.根据模态系数频谱，该两阶模态有明显的主要频率 1.265 kHz.第4阶POD模态类似第1阶模态，表现在转捩位置之后的翼型湍流边界层及尾缘附近的涡团结构，其尺度较大，频率较低.

图6 POD模态Fig.6 Modes of POD

为研究与气动噪声形成并向下游传播有关的流动结构，测点参考文献[10]，在翼型正上方10c处，平行于来流方向，向下游每0.05 m布置一个声压监测点.提取这些监测点的时域气动声压计算数据，并分析翼型非定常涡量场关于该列测点气动声压的EPOD，获得的EPOD模态特征值如图7所示.

由图7可以看到，EPOD特征值大小迅速衰减，前4阶EPOD模态就占声压波动能量的75%，相对于气动噪声，EPOD模态具有更好的降阶特性.

前4阶声压EPOD模态及其对应的模态系数频谱如图8所示.将得到的各阶EPOD模态单位向量化以与POD模态进行对比.由图8可以看到，声压EPOD模态不仅表现在翼型附近，更表现为尾迹中的涡团结构，可以发现经过尾缘后衰减，再逐渐放大、饱和后再衰减的类似波包的结构，该结构在射流噪声中被认为与气动噪声源有关[15].通过EPOD模态系数频谱可以看到，前几阶EPOD模态系数频谱具有宽频凸起的特征.第3、4阶EPOD模态系数在频率0.1～1.5 kHz范围内都具有较高的幅值，表明与气动噪声生成和传播的湍流结构频带更宽，波动更复杂.

图7 EPOD特征值Fig.7 Eigenvalues of EPOD

进一步分析翼型气动噪声源，不同攻角下翼型声压EPOD模态如图9所示.由图9可知，当翼型攻角为2° 时，声压EPOD模态在尾迹区的结构与翼型攻角为8° 时的情况较接近，表现出翼型前部气动噪声强度明显较尾部弱的特征(见图4(b))，说明在小攻角下，翼型尾部和尾迹的涡量波动主导气动噪声.而在翼型攻角为14° 时，分离涡从前缘开始脱落.通过EPOD模态可以发现，上方吸力面侧都存在不同尺度的、与气动噪声相关的湍流结构，并一直延伸至尾迹，而压力面上模态结构却相对较弱，与翼型攻角为2° 和8° 时的EPOD模态结构差异较大.在此攻角下，翼型上方吸力面侧的气动噪声强度显著高于下方.

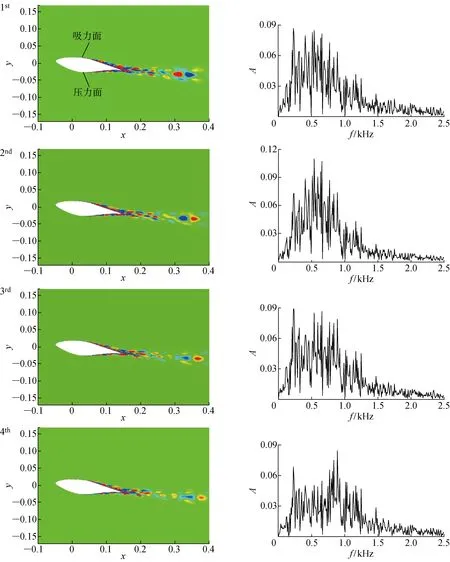
图8 EPOD模态Fig.8 Modes of EPOD

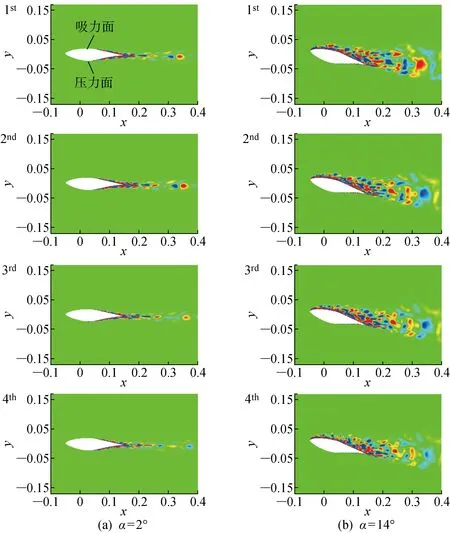
图9 不同攻角下的EPOD模态Fig.9 EPOD modes at different angles of attack

5 结论

本文采用大涡模拟方法对风力机S809翼型的非定常流场进行了数值模拟，并结合FW-H方法获得了翼型气动噪声，采用POD提取了非定常涡量流场的主要降阶模态结构，并采用EPOD方法，揭示了与翼型气动噪声最相关的非定常流动模态结构，获得如下主要结论.

(1) 采用大涡模拟对翼型流动的计算结果与实验测试值基本吻合，计算得到的翼型气动噪声在频谱图上呈宽频凸起特征，峰值频率在500～800 Hz范围.在小攻角情况下，翼型气动噪声指向性具有偶极子特征，随着攻角的升高，翼型前方以及吸力面侧的气动噪声强度有所增强.

(2) POD方法可以有效地降阶翼型非定常流场，前4阶POD模态占流场波动总能量的45%，模态结构均出现在翼型表面的中后部分，表明非定常流动的主要特征为翼型表面层流分离泡及尾缘附近涡团.

(3) 基于翼型气动噪声的非定常流场EPOD分析，前4阶EPOD模态占声压能量的75%，对气动噪声降阶较好.翼型尾迹中的湍流结构都被发现与气动噪声相关，表明尾缘噪声是翼型最主要的气动噪声源.而在大攻角下，吸力面分离中的湍流结构也与气动噪声相关.