面向加工领域的数字孪生模型自适应迁移方法

沈 慧， 刘世民， 许敏俊， 黄德林， 鲍劲松， 郑小虎

(东华大学 机械工程学院， 上海 201620)

数字孪生技术[1-2]，通过在虚拟空间实时映射物理实体状态以实现虚实强化.众多研究表明，数字孪生具有强大的应用潜力以提升制造业的经济效益[3-5].其中，设备和产品的质量监测是数字孪生在加工领域的研究热点[6-8].针对加工过程中的产品质量监测，有学者提出基于数字孪生对产品质量信息进行多粒度表达[9]，基于多智能体系进行加工过程数字孪生建模[10]，或建立零件高保真数字孪生模型[11]等，从而实现加工过程的质量监测和辅助决策.针对加工过程中刀具设备的状态监测，部分学者提出基于数据驱动的数字孪生建模[12-13]，通过加工信息的虚实交互，实现刀具磨损和剩余寿命的状态监测.在上述研究中，数字孪生大多基于固定工况建模，忽略了数字孪生模型在其他场景中的自适应能力，导致其性能随工况变化[14]而降低.

随着当前制造业个性化需求日益增长[15]，产生了多品种小批量的生产制造车间.在这类车间的生产现场中，需根据不同生产要求对工况进行调整(如刀具、夹具更换等)，因此对传统数字孪生模型产生了自适应工况变化的需求.现有研究主要从工况变化的两个方面来考虑数字孪生模型的自适应更新方法.因设备刀具等性能衰退导致工况发生被动变化的相关研究有：文献[16]针对机床磨损导致的性能衰减，建立具有时变性的数控机床数字孪生模型以适应工况变化；文献[17]提出基于两种时间尺度演化的数字孪生模型，实现在新增时间尺度上映射工况的动态变化.文献[18]建立了刀具数字孪生模型，实现刀具磨损和自身性能衰退过程的精确映射.基于工况被动变化的数字孪生建模可真实反映物理实体的实时状态，但在多品种小批量生产车间中，工艺条件变化(例如刀具、夹具更换等)对数字孪生模型精度也具有一定影响.因此，在另一方面，因工艺条件改变而导致的工况变化称为工况发生主动变化.部分学者对工况主动变化下的数字孪生模型可重构性[19-20]展开相关研究，然而大部分研究集中于数字孪生系统的快速重构框架，针对数字孪生模型自适应重建方法的研究极少.本文在现有研究的基础上具有以下创新点：① 在工况动态变化的多品种小批量生产车间中，构建具有可迁移性的数字孪生模型；② 针对数字孪生模型迁移方法的研究空白，提出数字孪生模型迁移流程；③ 根据工况变化的不同类型，提出两种数字孪生模型迁移策略，以提高模型迁移效率.

本文首先提出数字孪生模型迁移框架；其次，搭建可迁移的数字孪生模型，实现加工质量在线监测[21-22]；同时，结合迁移学习[23]相关理论，提出数字孪生模型迁移流程及迁移策略；最后，以钻削加工系统为例，在变化工况下对数字孪生模型自适应迁移的可行性进行验证.实验结果表明，迁移后的数字孪生模型仍能保持较好的预测精度.本文对数字孪生模型迁移方法的研究，为提高数字孪生模型变工况自适应能力提供了新思路.

1 数字孪生模型的自适应迁移框架

在多品种小批量的生产车间中，生产要求改变是导致工况发生动态变化的原因.为提高数字孪生模型在变化工况下的自适应能力，保证质量预测精度，提出了一种数字孪生模型迁移框架，如图1所示，其中: DT为各工况下的数字孪生模型.

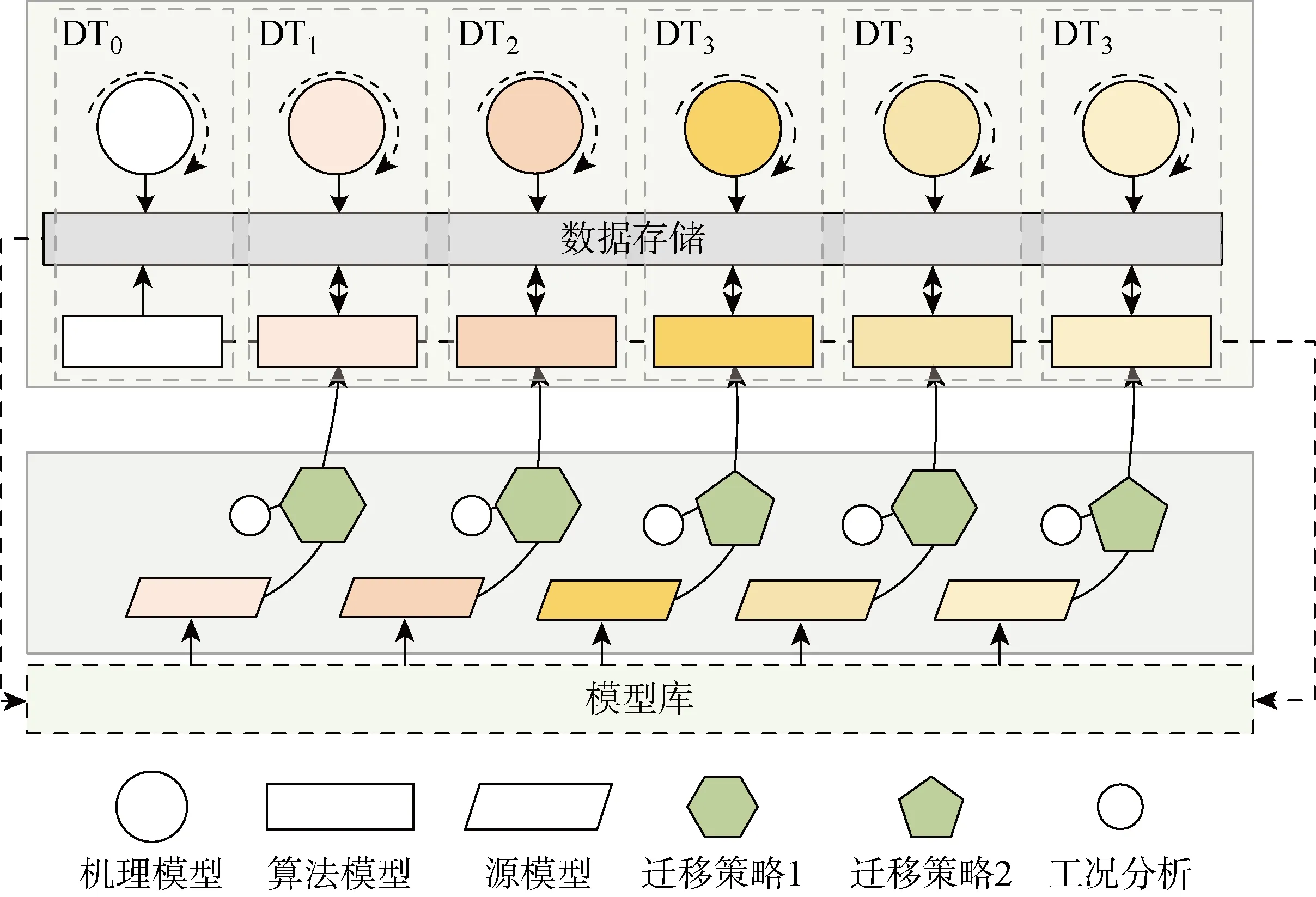
图1 数字孪生模型自适应迁移框架Fig.1 Adaptive transferring framework of digital twin model

该框架主要由数字孪生模型和模型迁移两部分组成.数字孪生模型主要包括质量预测模型，数据存储运算和模型库，可实现变化工况下的质量在线监测.其中，质量预测模型由机理模型和算法模型组成，是数字孪生模型和模型迁移的关键；数据存储运算和模型库为数字孪生模型迁移提供数据和模型基础.

当工况发生动态变化时，模型迁移可实现质量预测模型迁移更新，以提高新工况下数字孪生模型的自适应能力.本文将工况变化划分为简单工况变化和复杂工况变化，工况变化对质量指标影响较大则为复杂工况变化；反之，为简单工况变化.模型迁移首先基于新工况数据完成机理模型的自更新，然后从算法模型库中匹配待迁移的源模型，并基于工况变化分析(简单或复杂变工况)和对应迁移策略实现模型的迁移更新，从而获得适应新工况的数字孪生模型.最后，将迁移后的模型存储于算法模型库中，为后续其他变工况模型迁移提供丰富的模型基础.

2 建立可迁移的数字孪生模型

创建初始工况数字孪生模型是模型迁移的基础.本文提出一种可迁移的数字孪生模型，在变工况下实现自适应迁移更新，其结构如图2所示.其中：G1，G2，G3为工况1，2，3；T为加工时间信息；C1，R1，S1，H1分别为工况G1下的各质量指标的特征数据.物理空间中包括加工设备、刀具、工件、夹具和各类传感器，根据不同加工要求组成不同工艺条件.信息空间中包括数据预处理、数据存储、质量预测模型以及算法模型库.数据预处理主要对采集的时序数据进行时序信号碎片化，信号预处理和时频域特征提取.在质量预测模型中，机理模型(如铣削加工表面粗糙度机理[24]，钻削加工毛刺生成机理[25]等)用于提取时序数据的初级特征；而算法模型采用深度学习方法对时序数据进行深层特征提取和质量预测.通过机理模型和算法模型融合对加工质量进行预测.当工况改变时，通过特征数据运算，从算法模型库中匹配获得待迁移的源模型并进行自适应更新.迁移更新后模型产生的加工数据将存储于加工数据库，为后续其他变工况模型迁移提供数据支持.

可迁移的数字孪生模型具有两种时变性.第1种是当工况不变时，如图2中的常态数据流方向所示，数字孪生模型通过采集处理加工过程中的时序数据，对加工质量进行预测；第2种是当工况发生变化时，如图2中的动态数据流方向所示，数字孪生模型首先进行自适应更新，然后基于更新后模型预测加工质量.

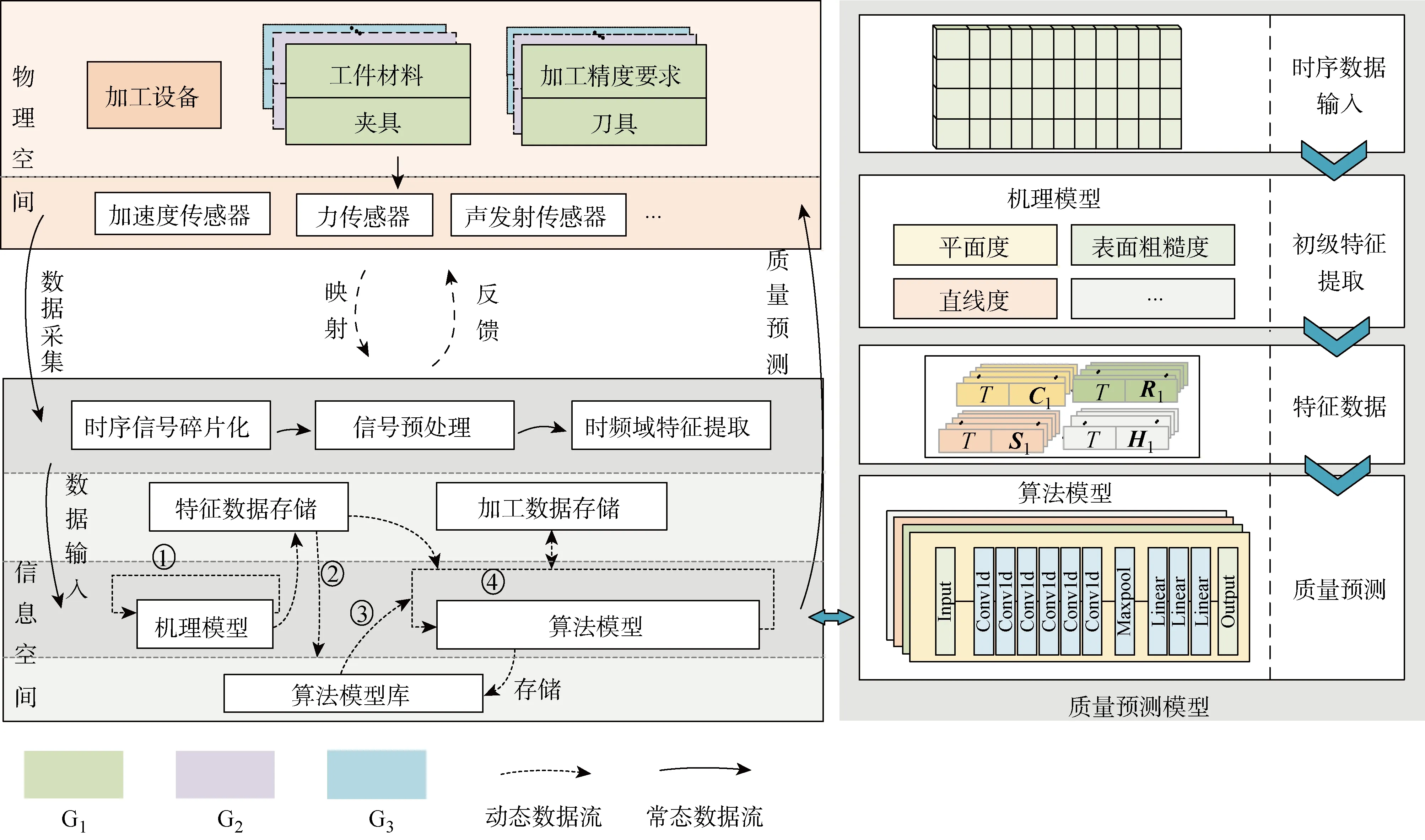
图2 可迁移的数字孪生模型Fig.2 Transferable digital twin model

3 变工况下的数字孪生模型迁移方法

针对上述数字孪生模型第2种时变性，提出数字孪生模型自适应迁移策略.本节首先介绍模型迁移的具体流程；随后，分别详述简单变工况和复杂变工况下模型所采用的迁移策略原理.

3.1 数字孪生模型迁移流程

数字孪生模型迁移可按迁移角度不同划分以下两种情况：同种质量指标间和不同质量指标间的数字孪生模型迁移.不同加工质量指标间实现跨领域模型迁移存在理论上的可行性[26]，但当其领域间不存在相似性或基本不相似，实际模型迁移会非常困难.因此，本文选择前者作为数字孪生模型迁移方法的初步探索，其具体内容如图3所示.其中：G0为初始工况； G4为工况4；Mn为源模型；M0，M1，M2，M3，M4分别为G0，G1, G2, G3，G4下的算法模型.

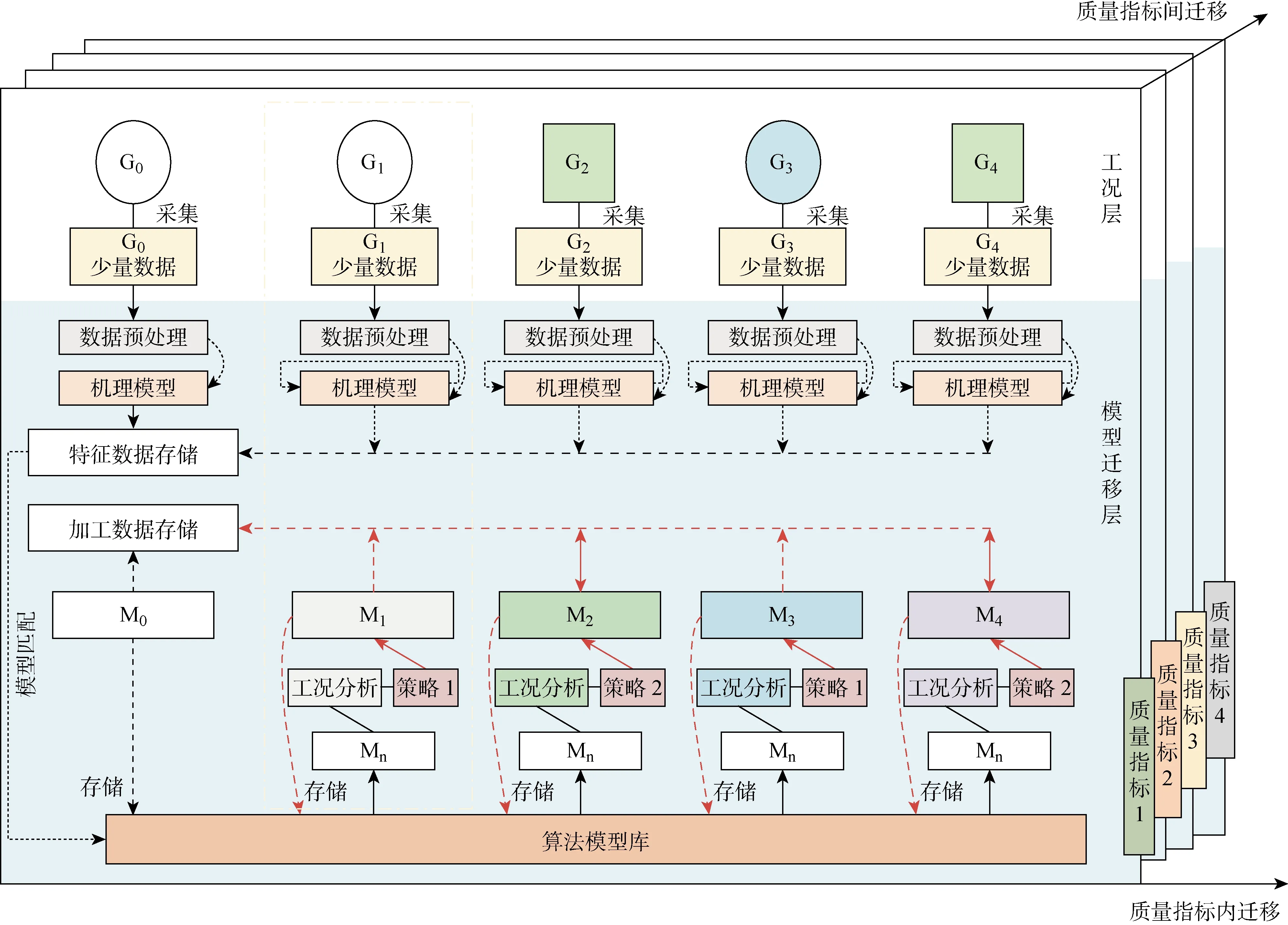
图3 数字孪生模型迁移流程示意图Fig.3 Transferring flow diagram of digital twin model

由图3可知，工况层描述了工件在不同工况条件下进行加工和数据采集.模型迁移层描述当工况变化时，数字孪生模型及时进行自适应迁移更新.面向加工的数字孪生模型可进行多种质量指标的在线监测(表面粗糙度，直线度和圆柱度等)，因此为实现数字孪生模型的完整迁移，需对其所有质量指标预测模型分别进行迁移更新.

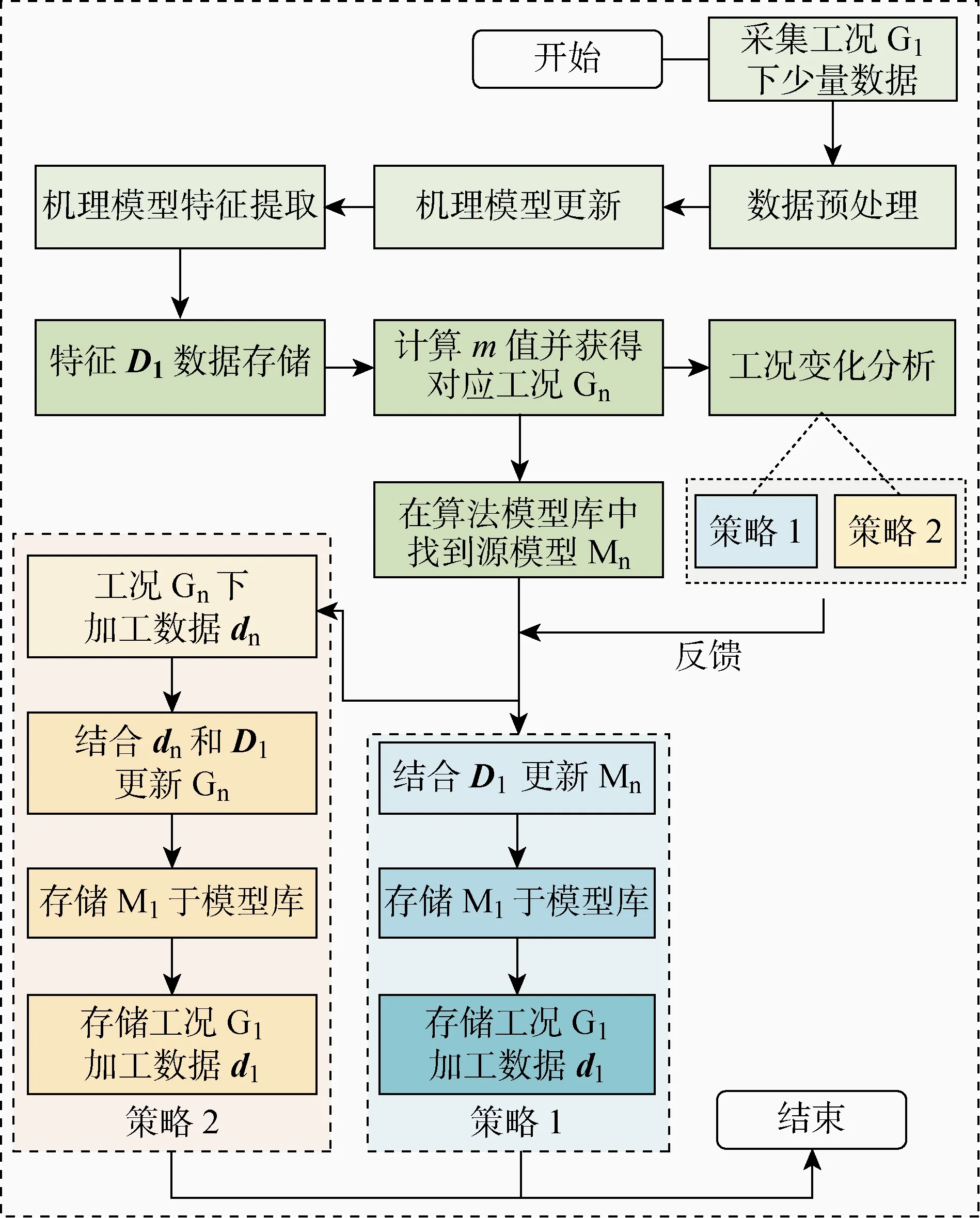
图4 数字孪生模型迁移步骤Fig.4 Transferring steps of digital twin model

下面将以一种加工质量指标为例，介绍数字孪生模型迁移的具体步骤，如图4所示.其中：D1为工况G1下的特征数据；Gn为源模型Mn所处工况；m为当前工况与其他工况的特征数据之间的最大平均差异(MMD)[27]的最小值；dn为源模型Mn对应工况Gn的加工数据；d1为迁移后工况G1下的加工数据.当工况改变时，采集新工况下少量数据并进行预处理获得原始数据集；基于原始数据，对机理模型进行实验参数微调以完成自更新；提取原始数据的初级特征，获得新工况的特征数据并存储于特征数据库； 分别计算新工况和特征数据库中存储的其他各工况特征数据之间的分布距离，并比较获得分布距离最小的特征数据集；基于该数据集，在算法模型库和加工数据库中进行索引，获得源模型以及加工数据集；由于源模型并不完全适用于新工况，需分析工况的变化类型，选择合适的迁移策略对模型进行迁移，最终获得新工况下的算法模型；最后，将该模型存储于模型库中，而后在加工生产中将其产生的加工数据存储于加工数据库.

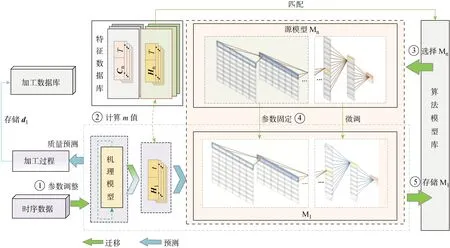
图5 简单变工况质量预测模型迁移Fig.5 Quality prediction model transferring under simple changing conditions

3.2 简单变工况下的数字孪生模型迁移策略

基于工况变化的假设，分析质量指标的相对工况变化类型.当工况变化对其特征数据的分布情况影响较小(如仅加工精度要求改变)，则属于简单变工况，需采用策略1对模型进行快速更新，其相关内容如图5所示.其中：Cn，Hn为源模型Mn对应工况Gn下的各质量指标的特征数据.

在工况G1下，基于原始数据调整机理模型并获得特征数据D1；以两工况特征数据分布情况最相似为目标，从模型库中匹配得到源模型Mn.本文采用MMD度量准则计算数据分布相似度，如下式所示：

(1)

式中：Φ为函数集；X，Y为两种工况的特征数据集；k(·)为核函数；xa，xb和ya，yb分别为X,Y的样本；N1，N2分别为X，Y样本数.通过求两种特征数据在映射函数上的函数值均值并作差，获得对应映射函数上的均值差异.通过搜索使均值差异最大的映射函数，得到MMD值.依次计算新工况和特征数据库中其他各工况特征数据的MMD值，并基于MMD最小值m，从算法模型库中索引获得Mn.

基于迁移策略1调整源模型Mn的具体实施步骤如下.

步骤1基于D1微调Mn，获得M1：简单工况变化下的两种特征数据分布相似，固定源模型前几层网络参数，利用特征数据D1进行全连接层的网络参数微调[27]；最终获得迁移后算法模型M1并存储于模型库中.

步骤2模型迁移更新后，存储加工数据d1：

迁移后模型可预测新工况G1下的实时加工质量，并将其产生的加工数据存储于加工数据库中.

上述简单变工况迁移策略用伪代码算法1描述如下.其中：Z1为微调函数；I为算法模型库；L1为工况G1下的机理模型；da为新工况原始数据；E为加工数据库.

算法1迁移策略1运行流程

输入源模型Mn，当前工况特征数据集D1.

输出当前工况预测模型M1, 加工数据d1.

/*模型迁移及存储*/ M1←Z1(Mn,D1)

I[1]←M1

/*加工数据存储*/

采集处理工况G1下的加工数据

D1←L1(da)

E[1]←d1←M1(D1)

return

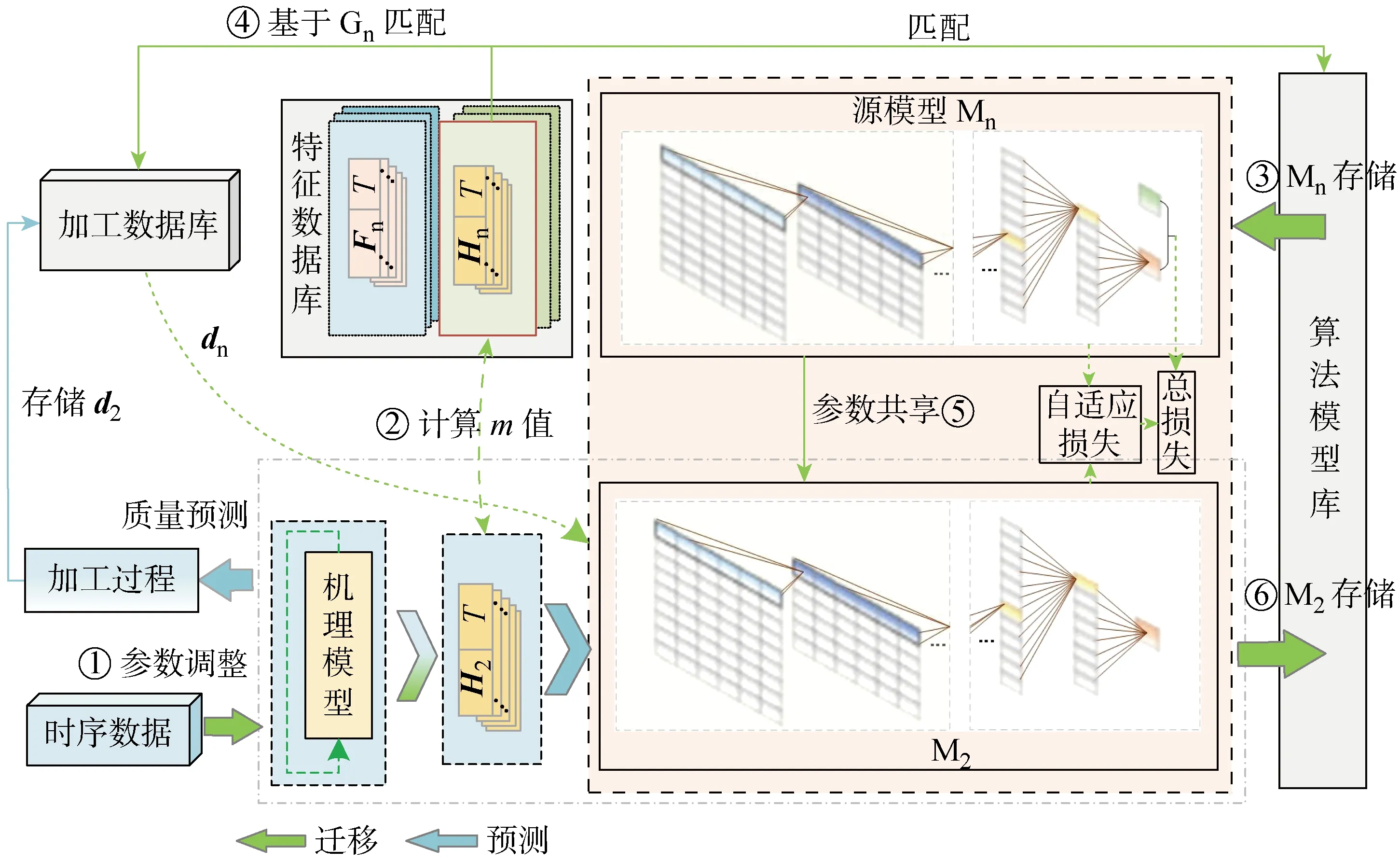
图6 复杂变工况质量预测模型迁移Fig.6 Quality prediction model transferring under complex changing conditions

3.3 复杂变工况下的数字孪生模型迁移策略

基于工况变化的假设，分析质量指标的相对变工况类型.当工况变化对其特征数据分布情况影响较大(如刀具更换)时，两种工况的特征数据分布不同，采用策略1更新源模型难以达到所需预测精度，当特征数据分布差异过大时，采用策略1甚至导致较差的效果.因此，针对此类复杂工况变化采用策略2更新源模型，其相关内容如图6所示.其中：H2为工况G2下的质量指标的特征数据；d2为工况G2下的加工数据；Dn为源模型对应工况Gn下的特征数据.

类似于简单变工况模型迁移，复杂变工况模型迁移需从模型库中匹配获得源模型Mn，随后采用迁移策略2对Mn进行迁移更新，获得新工况G2的算法模型M2.迁移策略2的具体实施步骤如下.

步骤1由工况Gn索引获得加工数据dn.

步骤2基于dn和特征数据D2，并结合迁移学习理论更新Mn，获得M2.

策略2的核心是采用深度神经网络的领域自适应[28]方法来解决两种工况下数据分布不同的问题.基于深度网络自适应方法进行迁移的关键在于确定合适的自适应层[29].由于模型预测任务和数据特征相同，故暂选择在全连接层添加自适应层，自适应度量采用MMD准则；同时，将源模型特征提取层的网络参数固定共享.策略2通过添加自适应层，使得模型训练总损失函数由带标签的加工数据的预测损失和两种工况下的数据自适应损失的权重加和组成，如下式所示：

l=lC(Dsou,ysou)+λlA(Dsou,Dtar)

(2)

式中：l为模型的总损失函数；Dsou为源模型的加工数据集；ysou为其对应加工质量的标签集；Dtar为新工况特征数据；lC(Dsou,ysou)为加工数据的预测损失函数；lA(Dsou,Dtar)为两种工况数据的自适应损失函数；λ为权衡两部分损失的权重参数.基于D2和dn对模型进行微调，从而完成复杂工况变化下的预测模型迁移.

步骤3模型迁移更新后，存储加工数据d2.

迁移后模型可预测新工况G2的实时加工质量，同时将其产生的加工数据d2存储于加工数据库中.

上述复杂变工况迁移策略用伪代码算法2描述如下.其中：Z2为微调函数；L2为工况G2下的机理模型.

算法2迁移策略2运行流程

输入加工数据库E, 被迁移模型Mn及其对应工况Gn, 当前工况特征数据D2.

输出当前工况预测模型M2, 加工数据集d2.

dn←E[Gn]

/*模型迁移及存储*/ M2←Z2(Mn,dn,D2)

I[2]←M2

/*加工数据存储*/

采集处理工况G2下的加工数据

D2←L2(da)

E[2]←d2←M2(D2)

return

4 案例和讨论

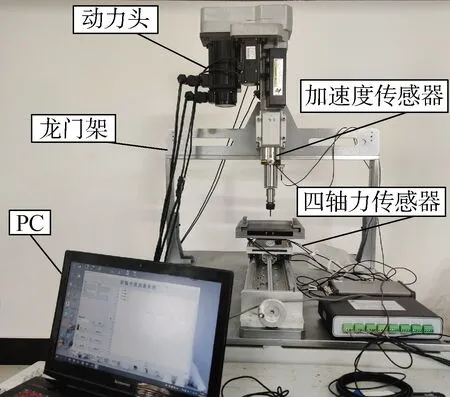
图7 自动钻削加工系统Fig.7 Automatic drilling system

实验搭建了钻削加工系统实物平台，如图7所示.在钻削加工后期，刀具离开工件时，部分未被切离的工件材料因挤压变形而形成出口毛刺.出口毛刺易产生且危害大，本实验以钻削加工出口毛刺高度质量指标为例，在变化工况下，对钻削加工系统数字孪生模型自适应迁移的可行性进行验证.

首先设定钻削加工系统初始工艺条件：采用合金钢直柄麻花钻在45钢上钻削6 mm的孔，主轴钻速为 2 000 r/min，进给量为0.16 mm/r.毛刺出口高度测量过程如下：利用线切割将工件切开，并利用螺旋测微仪采样毛刺上的6个点，最后以采样点的均值作为毛刺高度的实验结果.

收集初始工况下时序数据，并进行预处理：利用四轴力传感器采集钻削过程中的力信号，加速度传感器采集钻削过程中的振动信号，信号的时频域图像如图8所示，其中：a为加速度；t为时间；f为频率；A为幅度.使用小波对源信号进行降噪和统一化处理，同时按加工时间设置切分时序信号，并对每段时序信号进行时频域特征提取获得该工况的原始数据.

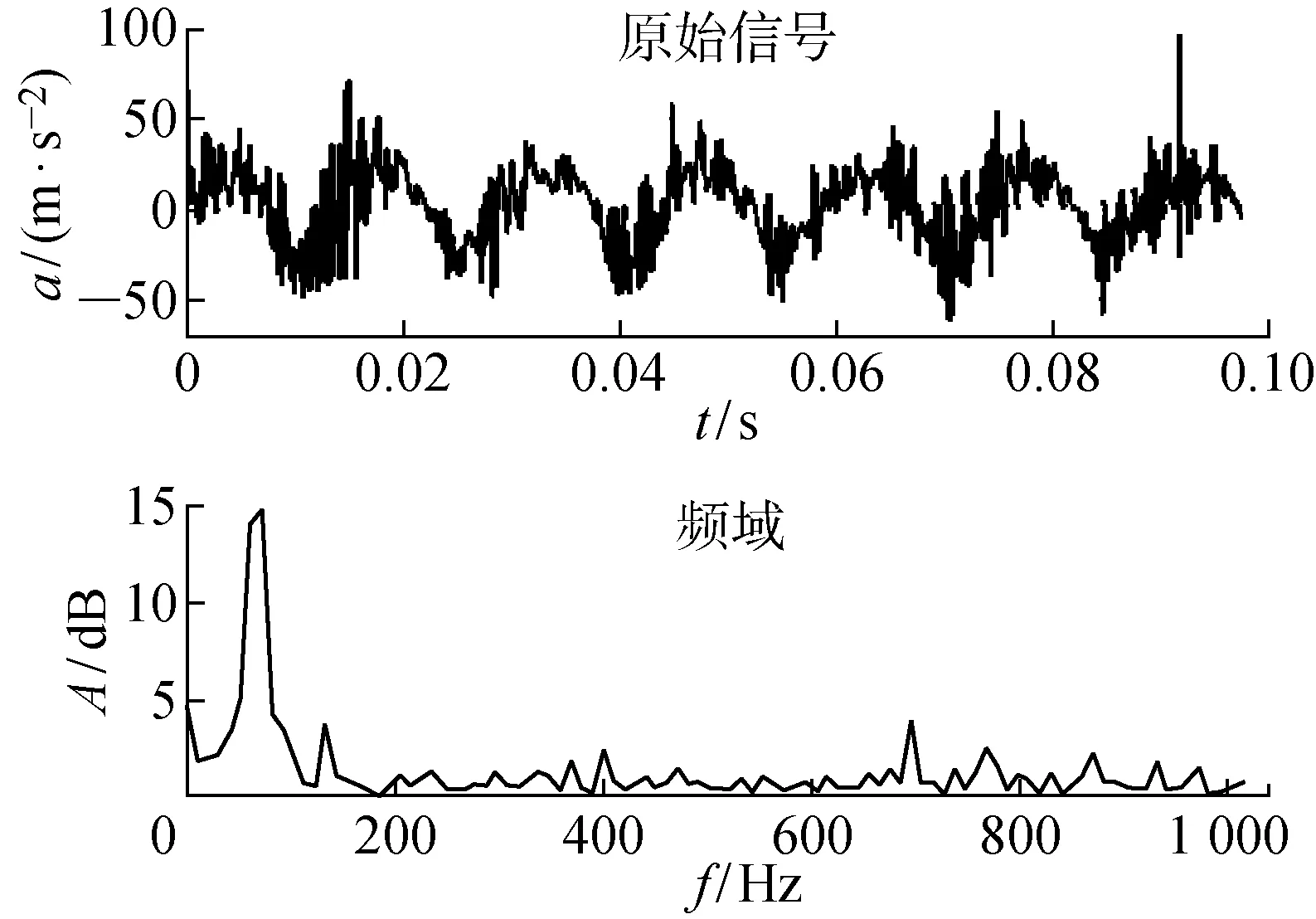
图8 初始工况振动信号时频域图像Fig.8 Time frequency domain image of vibration signal under current working condition

数字孪生钻削加工系统中毛刺质量预测模型由毛刺生成机理模型和算法模型组成.毛刺的产生与加工过程中的钻削状态以及材料韧性断裂状态密切相关，分别从两种极端条件下对毛刺建模.第1种不完全钻削加工，此时忽略韧性断裂因素，毛刺形成过程为纯粹的挤压塑性变形；第2种由韧性断裂和塑性挤压变形的共同作用，由于加工后期的加工硬化程度高，工件材料发生挤压变形，并在边缘部位产生断裂，通过预测工件初始裂纹的位置来预测毛刺高度，最后通过上述两种情况的不同能量组合来表示真实加工所产生的毛刺.毛刺生成机理模型参考团队以往的研究成果，如下式所示：

H(r,F,Bt)=

(3)

式中：Fe为轴向力影响因子；F为无量纲化的轴向力；μs为钻削过程存在的等效间隙；ks为间隙影响系数；Ps为锋角；ψ为收缩率；Bt为钻削过程中轴向和径向的振动振幅比值；Kε为应变影响因子；εf为破坏应变；h1为最大未切削厚度；r为半径；KH1和KH2为能量重构系数；Kb2、Kb1为实验系数.不同工况下机理模型存在细微差异，初选机理模型工况实验参数KH1=0.650，Kb1=0.005，Ks=55.975，KH2=1.001，Kb2=0.750，Kε=1.001；由于钻削加工过程中的信号具有强烈的时序特征，本文搭建一维卷积神经网络作为预测毛刺高度的算法模型.

首先，通过机理模型提取原始数据的初级特征，再基于该初级特征数据训练集对算法模型进行训练，最后将测试集带入该模型进行验证.图9为部分实验的预测结果.从图9中可以看出，虽然毛刺产生具有较大的随机性，但建立的初始工况预测模型结果基本符合实际毛刺高度.

基于上述建立的预测模型，在不同工况下对模型迁移可行性进行验证.本实验通过重新设定工艺参数(主轴钻速 2 200 r/min，进给量为 0.16 mm/r)以间接表示新工况1；采集处理新工况下的少量数据，进行预处理和时频域特征提取获得其原始数据.

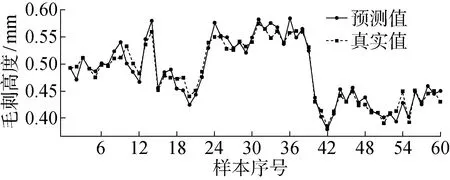
图9 毛刺高度预测模型的预测结果Fig.9 Prediction results of burr height prediction model

保持机理模型总体结构不变，基于新工况1的原始数据微调其部分实验参数(KH1=0.67，KH2=1.05，Kb2=0.33), 使其更好拟合原始数据，最终获得新工况1的机理模型.然后进行初级特征提取和训练集划分.

由于算法模型是在机理模型基础上进行质量预测，所以可根据迁移后算法模型的预测准确性来评估模型总体迁移效果.由于在迁移框架运行初期，故选择初始工况模型作为待迁移的源模型.其次，以工艺参数调整来间接表示工况变化，使得两工况间数据分布差异小，所以选择策略1进行迁移即：基于特征数据训练集，对源模型的线性层进行微调，最终获得迁移后模型.

为说明在工况变化下模型迁移更新的优势，本文将新工况1的测试集分别带入不同模型进行测试(迁移前模型，迁移后模型以及基于特征数据重新训练的网络模型)，比较各模型的预测效果，如图10 所示.

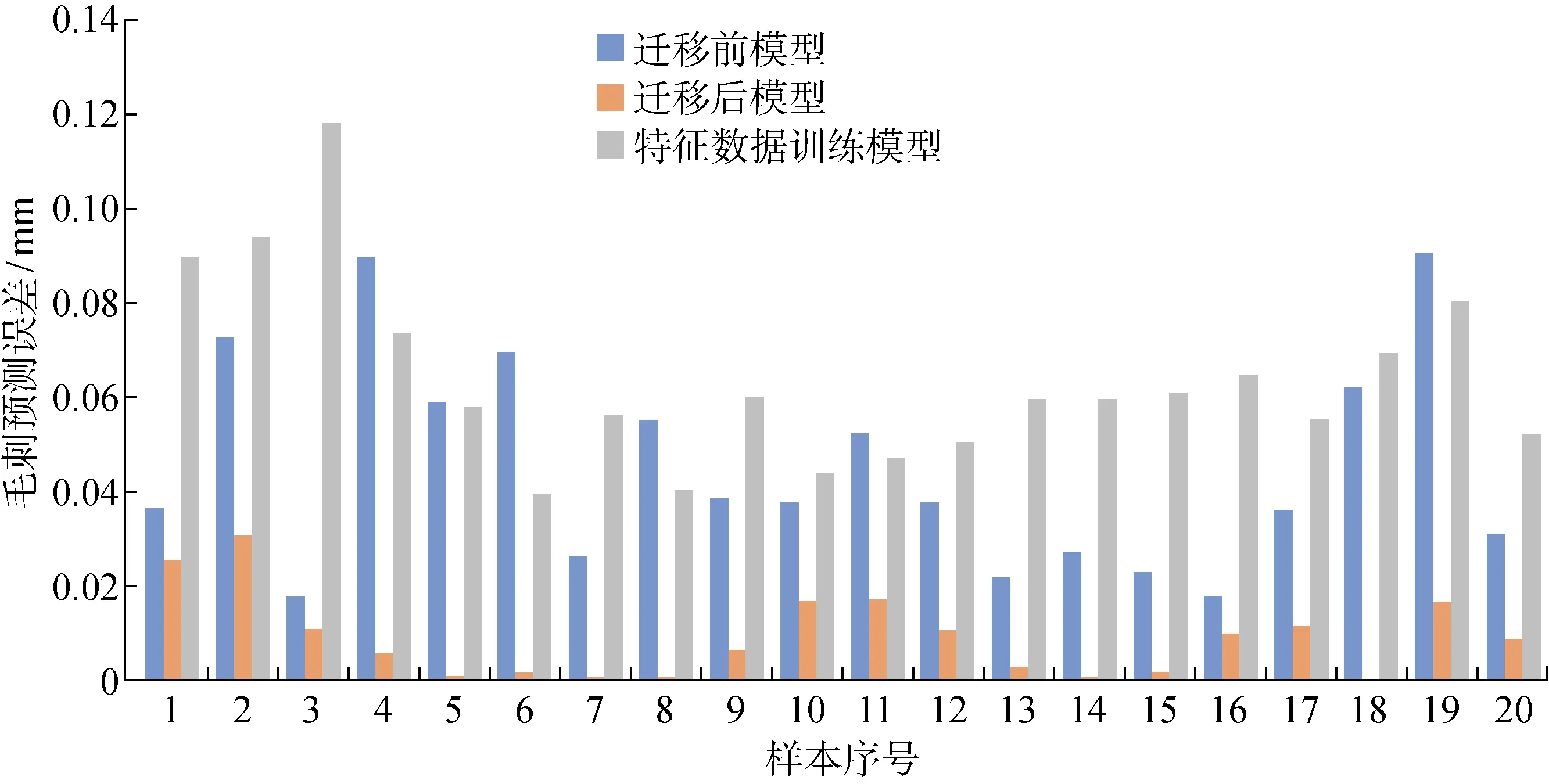
图10 新工况1下不同模型预测结果Fig.10 Prediction results of different models under new condition 1

采用平均绝对误差(MAE)对3种不同模型的预测结果进行对比，如表1所示.

另取一组工艺参数(主轴转速为 1 800 r/min，进给量为0.12 mm/r)来间接表示新工况2，进行实验验证.基于新工况2的原始数据对机理模型的实验参数进行微调更新(KH1=0.71，KH2=1.5，Kb2=0.24)；分别计算其特征数据与上述初始工况和新工况1特征数据的MMD值；通过计算发现初始工况相比较工况1，其特征数据分布和工况2更为接近，故选择初始工况模型作为源模型.3种不同模型在新工况2测试集数据上的预测效果如图11所示.

3种不同模型的预测结果对比如表2所示.

从实验结果可以看出，工况变化导致迁移前模型的预测性能下降，基于新工况少量数据重新训练的模型由于数据不足而导致过拟合.而迁移获得的模型，其预测效果相比较迁移前模型和特征数据训练模型具有一定优势.同时通过模型迁移，避免了数据量缺少和重新建模成本高的问题.该实验结果验证了模型迁移具有一定可行性，且有利于提高变工况下的数字孪生模型自适应能力.

表1 新工况1下不同模型预测结果对比

表2 新工况2下不同模型预测结果对比

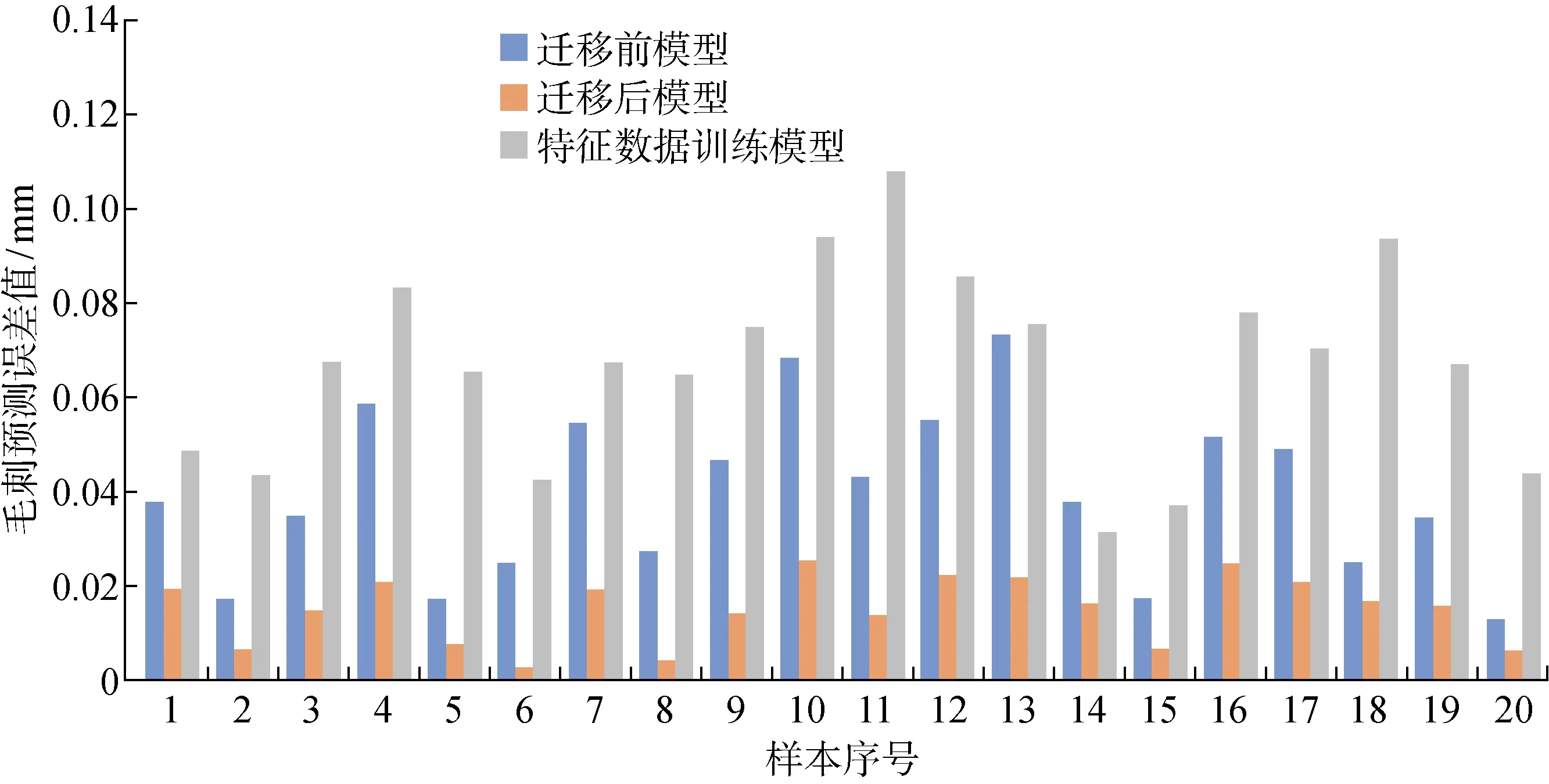
图11 新工况2下不同模型预测结果Fig.11 Prediction results of different models under new condition 2

5 结论

多品种小批量的生产制造车间中的数字孪生模型，需要具备针对变工况的自适应能力，论文提出一种新颖的基于迁移学习的数字孪生自适应方法，获得以下结论.

(1) 建立可迁移的数字孪生模型，可实现变化工况下的数字孪生模型自适应更新.

(2) 结合迁移学习理论，提出了数字孪生模型迁移策略，可满足不同工况变化类型下的模型迁移需求，提高模型性能和迁移效率.

(3) 搭建钻削实验平台，对数字孪生模型迁移的可行性进行验证，实验结果表明工况发生改变时，迁移后模型的性能具有一定优势，预测误差低于1.5%.

(4) 下一步将重点研究数字孪生模型中不同质量指标间预测模型的迁移方法，完善数字孪生模型迁移的方法体系.