刚性基底弹性转动约束矩形板各受载条件下屈曲分析

吴 韬， 莫时旭,b， 向勇斌， 邹泽群， 郑 艳,b

(桂林理工大学 a. 土木与建筑工程学院； b. 广西岩土力学与工程重点实验室，广西 桂林 541004)

随着钢材加工性能的改善，轻型化、薄壁化的钢结构设计在工程中有着越来越广泛的应用，薄板钢结构带来的稳定性问题越来越受到重视.部分充填混凝土-窄幅钢箱连续组合梁中支座处的下箱室由于充填了混凝土，底板和腹板的局部抗屈能力较大提高.但是要使其达到结构实际使用的要求，还需要进一步研究合理的截面尺寸，建立该种条件下薄板实用的局部屈曲强度计算公式.

近年来国内外学者从不同方向出发，提出对薄板屈曲问题的多种研究方法.文献[1-6]分别运用不同方法研究了各种边界条件矩形薄板在不同条件下的屈曲问题.

薄板屈曲的一大主流研究方法是能量法.能量法主要包括Galerkin法(伽辽金法)和Rayleigh-Ritz法(瑞利-里兹法)等.根据屈曲模态的不同，矩形薄板的屈曲理论又可分为两类.一类是双向屈曲问题.Timoshenko等[7]利用里兹法研究了在周边不同边界条件下受面内不同作用力的矩形薄板弹性屈曲理论模型.Qiao等[8-9]根据屈曲模态提出多种挠曲面函数，研究了四边受均布压力四边弹性转动约束矩形板的屈曲和受剪切荷载两对边简支两对边弹性转动约束矩形板的临界屈曲荷载.陈沐宇等[10]采用里兹法推导了弹性转动约束的钢混组合梁腹板在弯曲、剪切荷载单独作用下的临界屈曲应力.另一类是单向屈曲问题.Wright[11]研究了钢管约束混凝土的局部屈曲问题.毛佳等[12]运用里兹能量法获得弹性支承上非加载边弹性转动约束均匀受压矩形板的临界荷载计算公式.郑艳等[13-14]研究了刚性基底上非加载边弹性转动约束受面内线性压力作用下的矩形板局部屈曲问题.

国内外学者对基于刚性基底上弹性转动约束边界受面内复杂荷载作用矩形薄板的屈曲问题研究尚少，对于复杂边界条件下的屈曲问题多依赖试验和有限元数值分析[15-16]，这对于参数分析有较大局限性.获得具有刚性基底和弹性转动约束边界薄板的屈曲系数解析解，研究相关的理论公式仍极具意义.因此本文运用Rayleigh-Ritz法探究了在刚性基底上弹性转动约束边界薄板在四边受压、受剪的屈曲模式，分别获得临界屈曲系数的理论计算公式，依据相关规范中稳定相关性公式确定组合应力下的屈曲方程，并采用壳单元和弹簧单元建立相关有限元模型验证本文理论计算的适用性及正确性.还对不同转动约束刚度下的临界屈曲系数进行了参数分析.

1 刚性基底上弹性转动约束边界矩形 薄板屈曲分析

使用静力法求解板的屈曲问题，确定板的挠曲面函数必须归诸于板在相应荷载下的弯曲平衡微分方程在相应边界条件下的积分：

(1)

式中：w=w(x,y)为板的挠曲面函数；D为板的单宽抗弯刚度；Nx、Ny和Nxy为板中面沿x、y方向的压力荷载和xOy面内的剪力荷载;E、ν为板的弹性模量及泊松比；t为板厚.作为高阶偏微分方程，其求解是困难的.Rayleigh-Ritz法作为应用势能驻值原理求解稳定问题的一种近似方法，采用具有广义坐标的位移函数近似地代替真实位移曲面方程，也即将泛函变分问题转化为求解函数极值问题，将求解偏微分方程变为求解代数方程来处理.

1.1 刚性基底上弹性转动约束矩形板线性荷载压 屈分析

1.1.1计算模型以及挠曲面函数的选取 先考虑受压屈曲的情形.为了满足弹性转动约束的边界条件，挠曲面函数的选取必须满足一定条件.图1所示为刚性基底上双边弹性转动约束矩形板受压屈曲模型，图中γ为长宽比.通过选取带参数的多项式函数来模拟在y方向上的弹性转动边界[9]，选取一般三角级数来模拟在x方向上的固支边界和单向屈曲模态，则刚性支承上弹性转动约束边界矩形板压屈时面外位移函数的形式为

(2)

(3)

(4)

式中：m、n分别为x、y方向的屈曲半波数；am为广义坐标；a为板长；参数N为需根据板非加载边的边界条件方程个数确定.在式(3)中，为了构造弹性边界的特征函数，考虑幂级数[12]：

(5)

将式(5)代入式(3)，将式(3)、(4)代入式(2)，即可写出弹性转动约束受压矩形板的挠曲面函数为

(6)

式中：b为板宽.

图1 刚性基底上双边弹性转动约束矩形板受压屈曲模型Fig.1 Local compressive buckling mode of rectangular plate with rotationally restrained sides on rigid base

如图1(a)所示，矩形薄板的厚度为t；作用在刚性基底上，加载边y=0、y=b的弹性转动刚度分别为kb、kt.为分析方便，可以假设薄板的上下边界均布两种刚度的弹簧.

如图1(b)所示，N0和Nb为y=0和y=b处的压力荷载，简支边x=0、x=a受面内荷载Nx作用，弹性转动约束边y=0、y=b受荷载Ny作用，沿作用边线性分布，单位板宽的荷载表达式为

Nx=σxt

(7)

Ny=μNx

(8)

(9)

式中：μ为纵横荷载比；σ0为y=0处的压应力值；λ=(σ0-σb)/σ0为荷载梯度.

显然该位移函数满足边界x=0、x=a面外位移为0和转角为0的边界条件.根据边界y=0、y=b受弹性转动约束的边界条件，面外位移为0且板边弯矩与约束力矩相等，即满足：

(10)

(11)

(12)

根据弹性转动边界的边界条件方程个数，式(6)中N可取为4，则式(6)可改写为

(13)

式中：待定系数a0～a4是由边界条件式(10)～(12)确定.

将式(13)代入式(10)～(12)，求出待定系数a0～a4：

a0=0

(14)

(15)

(16)

(17)

(18)

式中：χb、χt为引入的无量纲刚度系数.

则挠曲面函数可表示为

(19)

式中：广义坐标bm=a1am；ai(i=2, 3, 4)的值由式(14)～(17)给出.

1.1.2压屈板各部分能量及其变分 板产生弹性屈曲变形的弯曲应变能：

(20)

上下边界受弹性转动约束的势能：

(21)

面内线性压力荷载所作的功：

(22)

对弯曲应变能求一阶变分为

(23)

边界弹性约束势能的一阶变分为

(24)

对压力做功求一阶变分：

(25)

根据最小势能原理有：

δΠ=δUe+δUΓ-δWN=0

(26)

式中：Π=Ue+UΓ-WN，为板产生屈曲变形时的总势能.于是

(27)

将求解泛函变分问题转化为求解关于bm的特征值问题，由式(27)可得关于bm的线性方程.为了使广义坐标bm存在非零解，则其系数矩阵的行列式必须为0.由此可求得矩形板在线性压力作用下发生屈曲的临界荷载Nx，其表达式可整理为

(28)

对于单位厚度的线性荷载：

(29)

式中：κ为受压屈曲系数.

1.1.3压屈板临界屈曲系数的解析解 将式(19)代入式(23)～(27)，可得到刚性基底上弹性转动约束边界矩形板受四边线性压力荷载时的屈曲系数解析解为

(30)

A1=η1+η2+η3

A2=η4+η5+η6

A3=η7+η8+η9

A4=η10+η11+η12

A5=η13+η14+η15

式中：长宽比γ=a/b；η1～η15为刚度系数χb、χt的函数；η10～η15还包含荷载梯度λ.

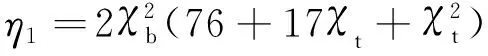
η11=18χb[18(52-31λ)+105(2-λ)χt+

η12=162[204(2-λ)+2(52-21λ)χt+

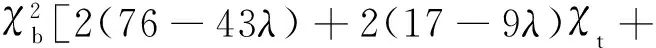
η14=2χb[12(95-51λ)+136(2-λ)χt+

η15=2[2 232(2-λ)+12(95-44λ)χt+

由此可见，屈曲系数κ是半波数m、刚度系数χb、χt、长宽比γ、荷载梯度λ和纵横荷载比μ的函数.

取λ=0，由式(30)可得，对于每一屈曲半波m=1, 2, …, 可绘制出κ与γ的关系曲线，如图2所示.

图2 κ与γ的关系曲线(λ=0, χb=χt=0)Fig.2 κ versus γ(λ=0, χb=χt=0)

(1) 当μ=0即Ny=0时，κ-γ曲线如图2(a)所示，可见每一支曲线先减再增，最低点处为临界屈曲系数.

各屈曲半波数m和γ相关，若表示半波m=p-1 与m=p两支曲线相交，则令：

κ|m→p-1=κ|m→p

(31)

式中：p-1表示前一半波数.式(31)为曲线交点(γp-1, p,κp-1, p)所满足.代入式(30)，可得：

(32)

p(γ)=γ-1(p)=

(33)

m=[p(γ)]

(34)

式(34)表示对p(γ)取整.

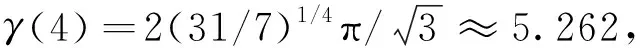
(2) 当μ>0即四边均受压时，κ-γ曲线的形态出现较大差异，如图2(b)所示.在特定条件下曲线的每一支单调递减，最终收敛于某一值，即临界屈曲系数.探索纵横荷载比μ对于κ-γ曲线单调性的影响，令∂κ/∂γ=0，代入式(30)得：

(35)

μ(γ)是单支κ-γ曲线的下界，若要使每一支κ-γ曲线单调，γ将趋于无穷大，即

(36)

当给定荷载梯度λ和刚度系数χb、χt时，式(36)给出每一支κ-γ曲线满足单调递减的纵横荷载比最小值.以λ=0、χt=10、χb=0为例，代入式(36)得μmin=0.845，即当纵横荷载比μ大于0.845时，屈曲系数κ始终随着薄板长宽比γ的增大而减小，并收敛于临界值κcr.

1.1.4压屈板临界屈曲系数参数分析 设当κ取得最小值κcr时，纵横比为γcr.令∂κ/∂γ=0，代入式(30)得：

(37)

式(37)也可通过式(35)的反算推出.

将式(37)代入式(30)，得临界屈曲系数：

(38)

进一步得临界屈曲荷载：

(1)γcr与χb、χt的关系.

由式(37)可得m=1时，γcr随χt、χb变化的关系曲线，如图3所示.μ=0，对于χb=0，χt=0, 5, 10, 50, 100时，γcr分别为1.519，1.350，1.302，1.237，1.226.由此可见，相同屈曲半波数时，γcr随着χb、χt的增大而减小.χt一定时，γcr随着χb的增大而减小.χt增大时，γcr-lgχb曲线整体下降，且γcr的变化幅度减缓.由于弹性转动边界的刚度系数χb、χt具有对称性，γcr-lgχt曲线随χb的变化规律与图3完全一致.

(2)κcr与χb、χt的关系.

由式(38)可得λ=0,χb=χt时，曲线κcr-lgχb随纵横荷载比μ变化的关系，如图4(a)所示.纵横荷载比越大，临界屈曲系数越小；纵横荷载比为负值时，Ny表现为拉力，因此临界屈曲系数大幅提升.

当μ=0,χb=χt时，曲线κcr-lgχb随荷载梯度λ变化的关系如图4(b)所示.荷载梯度越大，矩形板受拉区越大，临界屈曲荷载越大，相应的屈曲越难发生.

同样，当λ=0,μ=0时，曲线κcr-lgχb随单边弹性刚度系数的χt变化如图4(c)所示.随着χt的增大，κcr-lgχb曲线整体上升，但κcr的变化幅度减缓，可见板弹性转动边界刚度的提高对板抗屈能力的提升是有限的.

对χb取常用对数，可看出每条κcr-lgχb曲线都有上、下两条渐近线，分别代表矩形板弹性转动约束边界退化为固支和简支时的临界屈曲系数κcr.

图3 γcr与χb、χt的关系Fig.3 γcr versus χb and χt

图4 κcr与lg χb的关系Fig.4 κcr versus lg χb

1.2 刚性基底上弹性转动约束边界矩形板纯剪屈曲分析

1.2.1计算模型以及挠曲面函数的选取 刚性基底弹性转动约束矩形板受剪屈曲的计算模型如图5所示.

图5 刚性基底双边弹性转动约束受剪薄板屈曲模型Fig.5 Buckling mode of rectangular plate under shear with rotationally restrained sides on rigid base

与受压屈曲相似，矩形板受剪屈曲时的挠曲面函数满足式(2)，由分别满足x和y方向的边界条件函数耦合而成.x方向的特征函数仍选用式(4)，为构造y方向弹性边界的特征函数，考虑选用关于待定权重系数w1的三角函数一次组合：

(39)

(40)

(41)

但是受剪屈曲时由于倾斜角的存在，如图6所示，假设板的变形是线性，且满足小变形假设，则图示的理想倾斜节线的坐标近似满足以下关系：

(42)

(43)

式中：α为节线与y轴的倾斜角.

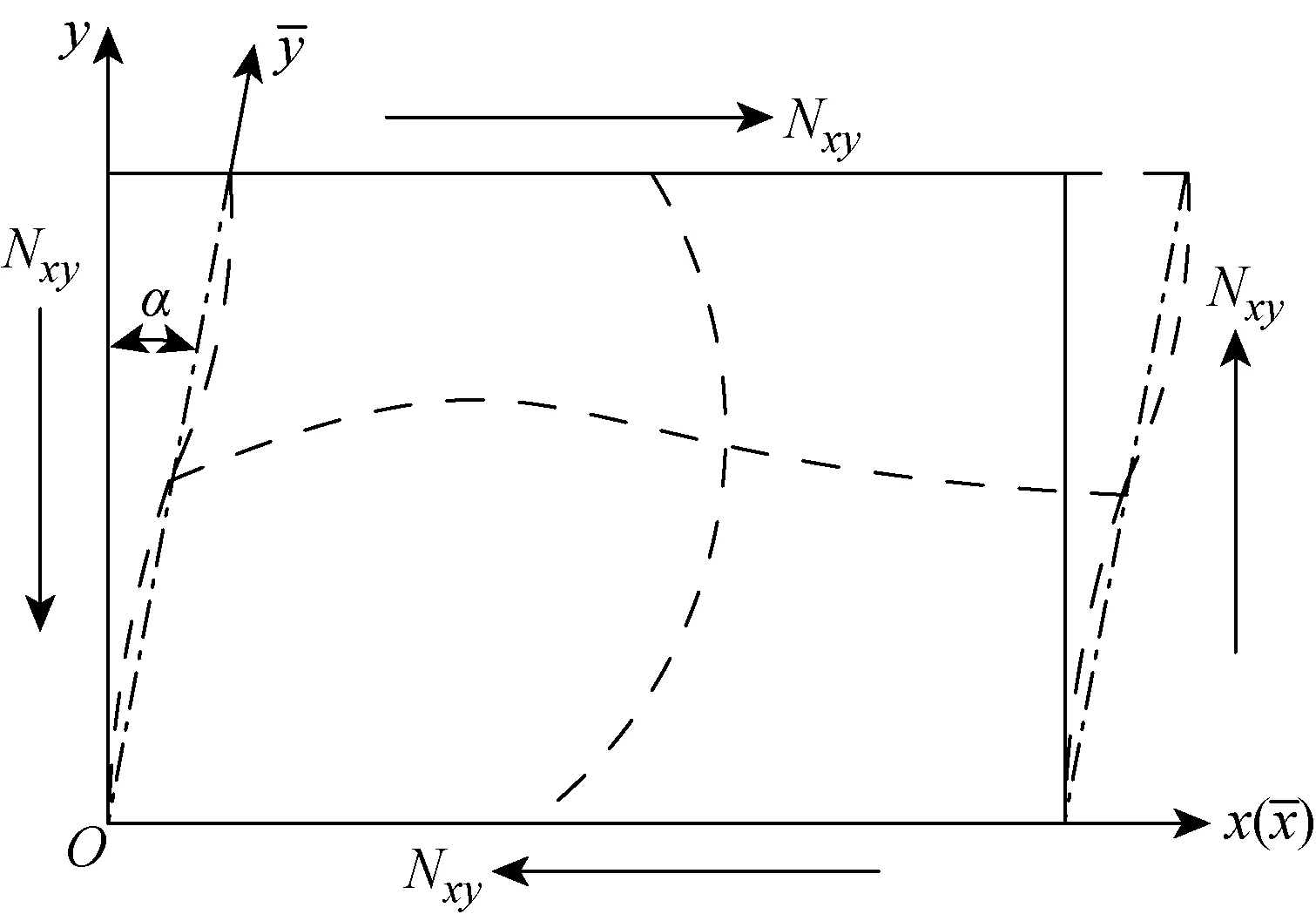
图6 受剪薄板屈曲变形示意图Fig.6 Buckling deformation diagram of plate under shear

为简化模型，将两弹性转动边界的刚度均取为ky，将式(39)～(43)代入式(2)，可写出刚性基底上弹性转动约束受剪矩形板屈曲时的挠曲面函数为

(44)

w1由板的边界条件方程式(10)～(12)确定：

(45)

1.2.2剪屈板各部分能量及其变分 刚性基底矩形板受剪屈曲时各部分能量与压屈板屈曲时各部能量基本一致.

将式(21)修改为

(46)

将式(22)修改为

(47)

同样可求得矩形板在剪切荷载作用下发生屈曲的临界荷载Nxy，其表达式同样可整理为

(48)

式中：κ2为受剪屈曲系数.

1.2.3剪屈板临界屈曲系数的解析解 为后续参数化研究，引入无量纲刚度系数：

将式(44)代入式(26)～(27)，可得到刚性基底上弹性转动约束边界矩形板受剪切荷载时的屈曲系数解析解为

(49)

式中：ξ1～ξ4为屈曲半波数n和刚度系数χ2的函数.

由此可见，屈曲系数κ是半波数m，n、刚度系数χ2、长宽比γ和节线倾斜角α的函数.

图7 受剪薄板κ与γ关系曲线Fig.7 κ versus γ of plate under shear

同样，当n=1时，由式(49)可知，对于每一屈曲半波m=1, 2, …,可绘制出κ与γ的关系曲线，如图7所示.若表示半波m=p-1与m=p两支曲线相交，令：

κ2|m→p-1=κ2|m→p

(50)

代入式(49)，可得：

(51)

p(γ)=γ-1(p)=

(52)

m=[p(γ)]

(53)

1.2.4剪屈板临界屈曲系数参数分析 设当κ2取最小值κ2cr时，长宽比为γcr，倾斜角为αcr.考虑到必有一组(γcr,αcr)使得Nxy取得最小值(Nxy)cr，令：

(54)

代入式(49)得：

γcr=

其中：

将γcr的表达式代入式(49)，得临界屈曲系数：

κ2cr=

(55)

(1)γcr与χ2的关系.

由式(55)可得m=1, 2, …时，临界长宽比γcr随刚度系数χ2变化的关系曲线，如图8所示.随着屈曲半波数的增加，γcr均匀递增；对于同一屈曲半波数，γcr随着弹性转动刚度的增大而递减.在m=1,χ2=0时，γcr约为1.91.

(2)αcr与χ2的关系.

由γcr的表达式可得临界倾斜角αcr随刚度系数χ2变化的关系曲线，如图9所示.临界倾斜角随χ2的增大而递增，在χ2=0, 100时，存在上下渐近线，αcr约为0.76和0.82.

(3)κ2cr与χ2的关系.

由式(55)可得临界屈曲系数κ2cr-lgχ2的关系曲线，如图10所示.κ2cr随弹性转动约束刚度系数χ2的增大而增大，可以看出κ2cr-lgχ2曲线同样存在上、下两条渐近线，分别代表矩形板弹性转动约束边界退化为固支和简支时的状态.

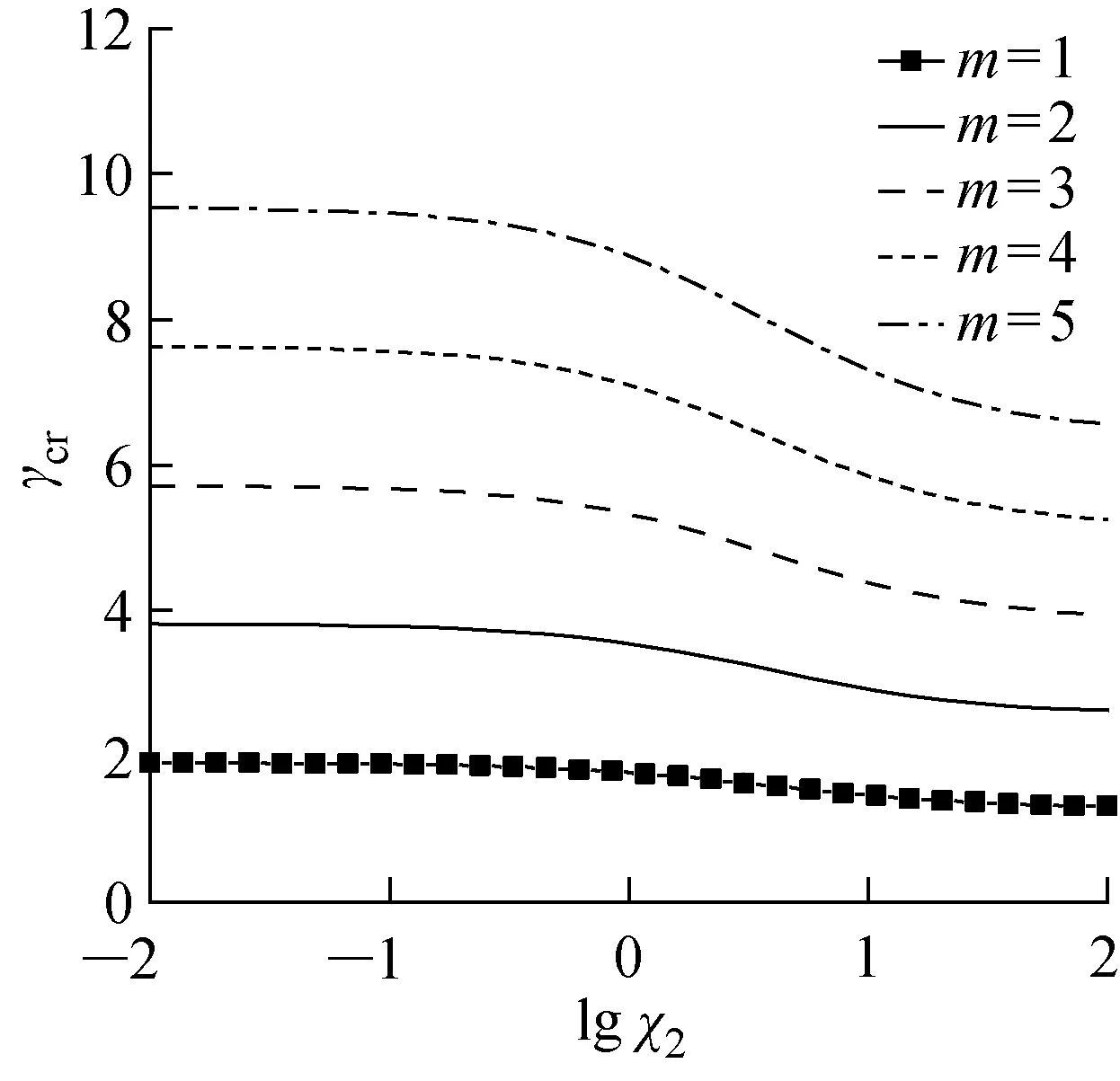
图8 γcr与χ2的关系Fig.8 γcr versus χ2

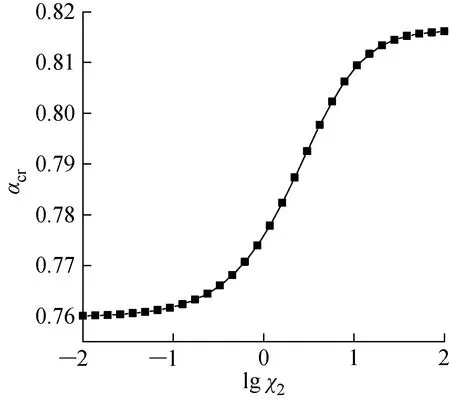
图9 αcr与χ2的关系Fig.9 αcr versus χ2

图10 κ2cr与χ2的关系Fig.10 κ2cr versus χ2

2 刚性基底上弹性转动约束边界矩形 薄板复合应力下屈曲分析

复合应力指的是矩形薄板面内同时作用有弯曲应力和切应力，这种情况更符合工程实际，如钢箱-混凝土组合梁受横力弯曲时，腹板上同时存在弯矩和切应力.钢-混组合剪力墙承受剪力的同时承受竖向荷载，故只研究矩形板在单一应力下的单侧屈曲行为是不够的.理论上找到符合复合应力下的屈曲模态的挠曲面位移函数比较困难，故求解复合应力下的稳定问题也较不容易，因此一般是以稳定相关性验算公式来判断屈曲问题.

2.1 复合应力下矩形板屈曲计算相关性公式

为了使复合应力下的计算公式简便且适用于工程上的验算，采用以下两个经验公式比较分析.

(1) 《钢结构稳定设计指南》[17]提出的在非均受压、剪切组合作用下腹板局部稳定性计算公式：

(56)

(2) Bijlaard[18]提出的偏心受压、剪切联合作用的屈曲计算公式：

(57)

式中：τcr、σcr分别为在纯剪、纯弯状态下的临界屈曲应力；τ、σ分别为复合应力状态下的剪切、弯曲应力.

2.2 矩形板弹性转动约束刚度计算公式

利用式(56)验算实际工程中板的屈曲，需要确定板的临界屈曲应力，而临界屈曲应力取决于板的临界屈曲系数，它又是弹性转动约束刚度系数的函数，因此在得到弹性转动约束刚度后，才可确定临界屈曲应力.以充填混凝土-钢箱连续组合梁的腹板为例，利用文献[14]，将约束钢板的宽度折减一半，以考虑内填混凝土对约束转动刚度的提高，得到钢板非加载边弹性转动约束系数的近似计算公式：

(58)

(59)

(60)

2.3 半充填式钢箱-混凝土组合试验梁负弯矩区腹 板屈曲分析

试验的主要目的是研究组合梁钢箱腹板的局部屈曲的行为，将试验实测的屈曲临界荷载与理论计算数据进行比较，验证理论公式的正确性.

2.3.1试验梁的设计 试验梁整体尺寸设计：试验梁纵长 4 400 mm，翼板宽 1 000 mm，厚120 mm，采用混凝土强度等级为C40，如图11所示.

钢箱梁高为300 mm，顶板、底板的宽度均为180 mm，顶板、底板厚度均为10 mm，腹板的厚度为 4 mm，高度为280 mm.在端部支座区设置横向加劲肋，钢梁采用Q235级钢板焊接而成.钢箱全长半充填混凝土高度为138 mm，强度等级为C40，试验梁横截面如图12所示.

图11 钢-混组合试验梁立体图(mm)Fig.11 Diagram of steel-concrete composite test beam (mm)

图12 试验梁横截面图(mm)Fig.12 Cross section of test beam (mm)

2.3.2加载方案与测点布置 半充填式钢箱-混凝土组合试验梁采用反向加载方式来模拟负弯矩区受力状态.将千斤顶置于地面，千斤顶压力通过置于上面的压力传感器来测量，产生的推力由分配梁通过一个活动支座和一个固定支座，分成两对称集中力分别作用于试验梁下翼缘的钢箱底板，两作用点间距为 1 400 mm.在试验梁混凝土翼板中轴线上距梁端200 mm处布置同样一活动支座和一固定支座，通过反力架提供反力.试验梁的计算跨径为 4 000 mm.如图13所示.

钢箱腹板表面布置的应变片如图14所示.在跨中两加载点之间的纯弯段(1.4 m)内设3个应变测量断面，用来测量负弯矩区的弯曲正应变.在靠近边支座处的东侧钢箱腹板表面设置3个断面粘贴应变花，用来测量剪应变.

图13 试验梁加载图(mm)Fig.13 Loading diagram of test beam (mm)

图14 翼板和钢箱腹板应变片布置图(mm)Fig.14 Strain gauges for flange plate and steel box web (mm)

2.3.3试验结果分析 在两点试验的加载值F=570 kN 时，钢箱负弯矩区支座腹板处发生板件局部屈曲，如图15所示.

图15 负弯矩区钢箱腹板局部屈曲失稳Fig.15 Buckling of web in negative moment region

假设钢箱腹板上的切应力均匀分布，梁截面满足平截面假定，则试验梁加载点处负弯矩区钢箱腹板屈曲时计算简图如图16所示.板长为屈曲范围400 mm，板宽为腹板高度280 mm.

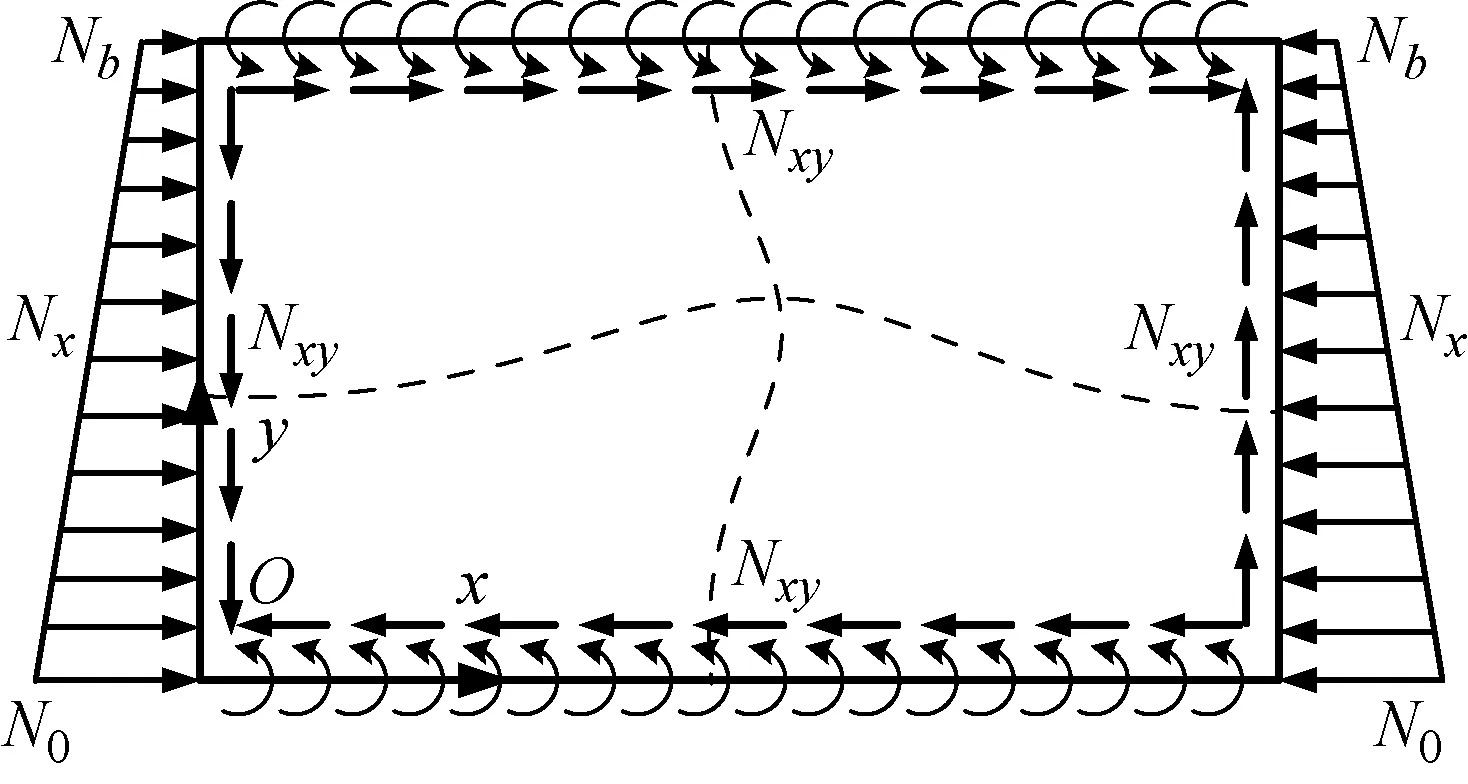
图16 负弯矩区腹板受复合应力屈曲计算简图Fig.16 Calculation diagram of box web buckling under combined stress in negative moment region

钢箱负弯矩区支座处腹板应变片数值如表1所示.根据平截面假设，截面钢箱腹板应变随梁高总体呈线性关系，可计算出腹板下缘即10 mm处正应变ε为 -1 132.36×10-6，腹板上缘即280 mm处正应变ε为 -319.06×10-6.

同样，在横力弯曲段靠近端支座处钢箱腹板表面设置3组应变花，由测量的应变数据可得屈曲时切应变γ为 -1 547.82×10-6.则试验梁钢箱腹板发生屈曲时实际应力为

表1 YY1截面屈曲时正应变数值表Tab.1 Normal strain of section YY1 during buckling

σ=Eε=226.47 (MPa)

(61)

(62)

式中：E为弹性模量.负弯矩区支座弯曲荷载梯度为

λ=(σmax-σmin)/σmax=0.718

(63)

利用式(58)，由图12可得腹板下缘的弹性转动约束刚度系数χb=56.05.钢箱上箱室虽未填充混凝土，但考虑到剪力钉对翼缘板弹性转动约束的制约作用[10]，仍考虑折减一半约束钢板的宽度，得到腹板上下缘的弹性转动刚度系数χt=χb=56.05.

根据式(30)、(49)可以计算得到弹性转动约束的板件在弯曲、剪切荷载单独作用下的临界屈曲系数，考虑腹板高度方向只有下箱室充填了混凝土，故对屈曲系数折减一半，可得：

κ=8.75，κ2=6.20

代入式(29)、(48)可得在弯、剪单独作用下的临界屈曲应力为：σcr=323 MPa，τcr=228 MPa.

那么稳定验算相关性公式可以写出：

文献[17]：

(64)

文献[18]：

(65)

试验结果和式(64)、(65)在弯-剪复合作用下腹板局部稳定性计算公式如图17所示.

图17 试验值与理论弯-剪复合屈曲应力曲线对比Fig.17 Comparison of test value and theoretical bend-shear complex buckling stress

由此可知，本试验结果略低于文献[17]和文献[18]弯剪复合屈曲应力值，吻合良好，验证了本文对于刚性基底弹性转动约束矩形板受压屈曲和受剪屈曲系数求解的准确性.计算结果比简单地将非加载边界按简支或固支处理的计算结果更符合钢箱-混凝土梁腹板局部屈曲的试验结果.

3 部分充填式钢箱-混凝土组合梁负 弯矩区腹板屈曲有限元分析

由于全梁模型钢箱腹板的临界屈曲系数受腹板自身宽厚比、上下翼缘板宽厚比、剪力钉的连接刚度、混凝土充填高度、加载点和弯剪比等诸多因素的影响，为了控制单因素条件得到复杂受力下的弯-剪复合临界屈曲应力，对在受力状态(图(16))下的腹板单独建立ANSYS有限元模型，并结合试验及本文理论解比较分析其适用性.

薄板模型采用Shell63四节点弹性壳单元.对于弹性转动边界和刚性基底，分别采用两种Combin14弹簧—阻尼器单元模拟，分别赋予沿板边的扭转自由度和垂直于板面的自由度，使弹簧单元只有绕坐标轴的扭转刚度或沿坐标轴的轴向拉压刚度.需要指出的是，在薄板底面布置双向拉压弹簧，用来模拟在弹性基底上的薄板屈曲行为.本文通过将底面弹簧的刚度系数χ1控制在一个较小值以模拟试验中半填充混凝土钢箱腹板的屈曲特性.

引入的无量纲刚度系数χ1定义为

(66)

式中：k0为弹性基底的支承刚度，分布化后作为每个底面弹簧的倔强系数.χ1描述了底面弹簧和矩形板刚度的相对大小.

为满足重复分析的需要，编写了模型建立和特征值屈曲分析的命令流程序.采用先生成全部节点，后建立相关单元的模式，可快速便捷建立有限元模型.设定主要参数有：χ1、χ2、γ、λ和弯剪比β.采用国际单位制，薄板的弹性模量取E=2.1×1011Pa，泊松比μ=0.3，板厚t=0.014 3 m.为方便起见，板宽b取为定值1 m，根据γ确定板长a.模型沿x轴方向的板边为弹性转动边界，同时板四边简支，对于不与薄板相连的弹簧单元节点，约束其全部自由度.布载时首先在模型上作用一个较小的剪力值，称作扰动值，再根据弯剪比β确定作用的压力值，分布化后作用在各个节点上.

根据本文第2部分的试验，等比例缩放板的尺寸a=1.43 m，b=1 m，t=0.014 3 m；λ=0.72；χ2=56.1.鉴于刚性基底和弹性基底的定量关系尚不明确，χ1分别取0、5、10进行分析.弯-剪屈曲荷载有限元计算结果如表2所示.

表2 在基底刚度χ1=5时的弯-剪复合屈曲荷载值Tab.2 Load of bend-shear complex buckling at χ1=5

图18所示为在3种基底刚度下共39个模型屈曲时的弯-剪复合应力值，用光滑曲线相连与图17通过理论计算的规范曲线和试验值对比发现，有限元结果和本文计算理论曲线走向一致，基底刚度系数χ1=5的曲线与本文理论曲线吻合较好，证明本文理论计算的可行性.半充填式钢箱-混凝土组合试验梁由于只在下箱室充填了混凝土，故负弯矩区腹板不能完全视为处于刚性基底之上，而是给予基底一个刚度系数较为合适.通过有限元分析可得，腹板基底的刚度系数略低于5.腹板屈曲在3种基底刚度下的一阶屈曲模态如图19所示.

部分充填式钢箱-混凝土组合梁全梁1/4纵横对称Abaqus模型腹板特征值屈曲模态如图20所示.由此可见，负弯矩区位于中支座正下方的腹板由于钢箱下箱室充填的混凝土，屈曲强度有了较大提高.而在充填混凝土范围之外的腹板则较易发生局部屈曲.说明无侧向混凝土约束的腹板屈曲强度低，混凝土的充填能显著提高钢箱组合梁负弯矩区腹板的抗屈能力.

图18 有限元值与理论弯-剪复合屈曲应力曲线对比Fig.18 Comparison of FEM value and theoretical bend-shear complex buckling stress

图19 3种基底刚度下腹板的一阶屈曲模态Fig.19 First set of buckling modes of web plates at 3 kinds of base stiffnesses

图20 部分充填式钢-混组合梁模型屈曲模态Fig.20 Typical buckling mode of partially filled steel box-concrete composite beams

4 结论

(1) 本文根据受压受剪矩形板屈曲变形特点，分别提出不同的挠曲面函数，通过利用Rayleigh-Ritz法导出了刚性基底上弹性转动约束边界矩形薄板在线性压力荷载单独作用下和剪力单独作用下的屈曲系数理论计算公式，形式较为简洁，便于参数化分析，为进一步分析匀质矩形薄板在复合应力条件下的屈曲问题提供了理论依据.

(2) 通过对屈曲理论解求极值，分析了受压临界屈曲系数随边界刚度系数χb、χt的变化规律，对比分析了在不同纵横荷载比μ和不同荷载梯度λ下受压临界屈曲系数的变化曲线；同时也分析了受剪临界屈曲系数随χ2的变化规律，证实了弹性转动约束边界不可简单地视为简支或固支边界.

(3) 通过一根半充填式钢箱-混凝土组合试验梁的反向加载试验分析了负弯矩区腹板的屈曲情况.结合文献复合屈曲应力公式，运用本文推导的单独受压、剪屈曲系数公式计算出临界压、剪屈曲应力，结果显示试验值位于根据本文理论解绘出的复合应力曲线之上，证实了本文理论解的可行性.

(4) 建立腹板的有限元模型，借助于对弹性基底的研究方法，对试验梁半充填混凝土的腹板赋予弹性基底刚度系数，数值分析表明，有限元结果和本文计算理论曲线走向一致，弹性基底刚度系数χ1=5的有限元曲线略高于本文理论曲线，半充填混凝土试验梁负弯矩区腹板基底的刚度系数略低于5.