明文图像可逆信息隐藏综述

2022-01-27 04:26欧博殷赵霞项世军

中国图象图形学报 2022年1期

欧博，殷赵霞，项世军

1. 湖南大学, 长沙 410082； 2. 安徽大学, 合肥 230601； 3. 暨南大学, 广州 510632

0 引言

可逆信息隐藏自诞生以来，就受到了业内的广泛关注。通过此技术，载体可以预先嵌入特定的秘密信息，然后在提取端无损恢复出秘密信息和原始载体。而在传统信息隐藏中，嵌入、提取操作会对载体造成永久性的改变。对于司法、医学、军事等强调载体内容精确性的应用领域，这种信息损失往往不可接受，因为原始内容的信息价值要超过水印价值，用原始信息的损失换取水印信息的嵌入得不偿失。在此背景下，学者们提出了可逆信息隐藏(又称可逆水印)技术来满足此类重点领域的需求。最早的可逆概念来自于20世纪九十年代的美国分界。此后，各类算法相继出现。今天，可逆算法已逐步应用于图像真实性认证、医学图像处理、视频纠错恢复、立体图像编码、工程矢量图像恢复等领域。同时，可逆研究面对诸如人工智能等技术所引发的社会新业态、新问题，也开始展现出变革、融合等不断发展的新趋势。

限于篇幅和能力所限，本文主要介绍明文域的图像可逆信息隐藏算法。

1 BMP图像可逆水印回顾与发展

1.1 3大发展阶段

位图(Bitmap, BMP)图像泛指未经过明显压缩、保留了自然图像大部分冗余性的图像文件格式。该格式对于算法研究有很强的普适性，各类算法、理论都能在其身上“一展身手”，并得到很好的发展。相关综述颇多，其中以Shi等人(2016)撰写的综述最新、最权威也最全面。鉴于此，本文不再过多重复，而更多关注研究发展脉络和未来发展方向。本文以可逆信息隐藏发挥影响力、受人关注为角度，将BMP图像的可逆研究划分为3个阶段。

第1阶段：从“0”到“1”。这是一个开创性的阶段，实现了从无到有的发展。作为可逆研究的源头(Tian，2003；Alattar，2004；Celik 等，2005；Ni等，2006；Chang等，2006；Thodi和Rodriguez，2007，Coltuc 和Chassery，2007a)，它们存续时间最长、引用次数最多，影响力也最大。其中Tian(2003)、Ni等人(2006)、Thodi和Rodriguez(2007)、Coltuc和Chassery(2007a)先后提出的差值扩展算法(difference expansion, DE)、直方图移位(histogram shifting, HS)、预测误差直方图扩展(prediction-error expansion, PEE)和整数变换(integer transform, IT)奠定了此项研究的基础，引领了此学科研究的发展。今天研究者依然能够通过回顾这些经典从中获得灵感。

第2阶段：从“1”到“100”。这是承上启下的时期，即继任者将基础理论丰富发展，加以变化，进一步深化理论应用的阶段。其中Li等人(2011，2013b，2015)提出了自适应嵌入理论，并具象为若干实际算法，如扩展PEE为2维映射(Ou等人，2013)、像素排序预测算法(pixel value ordering, PVO)、多直方图平移(multiple histograms modification, MHM)等技术。此外，Zhang等人(2012)和Zhang等人(2013)分别推广了基于压缩的思想，提出了先进编码与可逆嵌入融合的理论算法。这一时期成果出类拔萃，独具特色。

第3阶段：从“100”到“1 000”。此阶段是当前研究所处的阶段。从创新上看，因可依循前人成熟框架，难度略微降低。但从增量上看，需要增加“900”，并由点及面地推广可逆算法，任务并不小。要真正做好，需要耗费的时力将要超过前两阶段，难度和意义也不亚于前者。这也是当前可逆研究的难点和主要任务。此外，该阶段研究受限于旧的应用场景，突破性的进展暂未出现。但值得庆幸的是，从总体引用次数在不断增加这一事实分析，从事可逆研究的人数在增加、基础也在加厚，学科潜力依然存在。另一方面，随着人工智能技术的推广应用，水印技术被认为可以作为一种事前防御的手段，展现出新的生机。可逆水印若能在此方面有所作为，解决智能时代的安全问题，将极具价值。

1.2 经典算法解读

就空域处理而言，可逆实现的代表性框架共有3类：第1类是基于无损数据压缩(lossless data compression)设计而成的。该方案从图像中选取合适的特征，然后利用成熟的编码压缩技术来完成数据压缩，空出空间并直接填补上隐密信息。第2类方案受哈尔小波变换启发设计而成，取名为差分扩展算法，并逐步衍生为后续的整数变换、预测残差扩展等算法。第3类框架是对图像直方图进行移位，通过直接改变图像的统计特性来完成信息嵌入。下面分别对这3类算法做简要描述。

1.2.1 基于数据压缩的理论探讨

从编码角度看，可逆信息隐藏可以理解为载体在嵌入前后信息熵的变化问题。基于该思想，这类算法直接对载体的部分信息进行无损压缩，从而节余出空间来完成隐密信息的嵌入。在此过程中，嵌入者先用无损压缩算法迫使载体实现熵减，转为更紧凑的表达形式，然后再嵌入水印信息(一般为加密后的随机序列)迫使其又向无序方向变化，即熵增。一减一增的过程，即为可逆嵌入的实质。其难点在于增减过程还必须保持载体信息间固有的主要联系，即图像语义。增减变化太大，载体的语义信息就被破坏；增减太小，则容量受限。大多数情况下，介于其中是最好的选择。此平衡性依赖于对具体应用的理解和算法的巧妙设计来如实满足。此外，算法设计的人为偏差也会导致熵的增减，影响平衡性。该研究推荐关注率失真模型和最优转移概率模型等研究(Zhang等，2013； Hu等，2015；Zhang，2013)。

1.2.2 差分扩展算法(DE)

DE算法将图像元素单个处理，依次对单个像素或像素向量实现可逆操作，从而实现全图的可逆性。对应的科学问题变为，如何将任意一个像素对(pi,pi+1)可逆地转为(p′i,p′i+1)，如下式所示

(1)

式中，符号|·|为上取整函数，b为二进制比特。该算法采用的是整数哈尔小波变换的思路，以两个像素的均值为水印嵌入的基准，在此基础上微小改变均值，就能兼顾水印嵌入和图像语义表达。两两像素互为参考为一个基本嵌入单元，每对像素嵌入1 bit信息。依靠此思路推广到多个像素互为参考，则得到整数变换算法。DE算法实现可逆性需要较多的辅助信息，后续代表性算法大多在此问题上讨论优化(Kim等，2008；Hu等，2006，2008，2009)。此外，DE也具备较好的应有扩展性，如早期的2维矢量图水印算法(Wang等，2007)和适配人眼感知的水印算法(Yang等，2009)都是该类算法直接应用的成功例子。

1.2.3 整数变换(IT)

将DE推广为更一般的情况，可逆问题转为修改像素向量(p0,p1,…,pn)为(p′0,p′1,…,p′n)，如下式所示

(2)

一个长度为n的向量可嵌入的容量为n-1比特。多个像素联合考虑后，它们的均值更稳定，不易受到水印嵌入的扰动。这类方法能够统筹多个像素联动嵌入，可以实现很高的水印嵌入率。在同等条件下，若减少水印嵌入，则该方法会表现出较强的鲁棒性。整数变换继承了DE的优点和不足，因而也需要考虑位置图等辅助信息的优化，性能出色的算法都比较巧妙地记录了位置信息(Lee等，2007；Weng等，2008)。

1.2.4 预测残差扩展(PEE)

PEE算法设计模块丰富，相关研究较多。完成一个PEE算法设计包含特征选取和特征修改两个步骤。其中，嵌入特征不再是简单的像素差值，而是预测残差。这相当于对差值做评分，“好”的差值能够有利于后续的水印嵌入。残差“好”与“坏”由评价指标决定，相应的预测器辅助实现这一目标。在以PSNR(peak signal-to-noise ratio)为主导的评价体系中，像素改动越小，算法性能越优异，因而预测越准确，让残差接近于0便是“好”的标准(Luo等，2010； Coltuc，2011,2012；Coatrieux等人，2013；Dragoi和Coltuc，2014)。这个步骤也是重新构建嵌入特征的过程，把原有的像素分布转为预测残差分布。因残差分布近似于拉普拉斯分布，图像信息表达更紧凑，实现了有效熵减。预测残差计算公式为

(3)

接着修改残差，修改方式与差分扩展算法类似，差别在于参考基准由均值变为预测值，修改公式如下

(4)

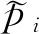
1.2.5 直方图移位(HS)

HS基于简单图像统计特性(即不同灰度值的像素个数)来完成可逆嵌入提取。因为图像的总体统计特性不会大幅改变，因而可以作为可逆参考的基准，也能够保持图像语义。HS的优点在于简单、有效。它的迁移性最强，基于统计类、全局性修改的算法设计均可借鉴和使用。HS在得到直方图后选择两个嵌入点(l,r)，然后对满足该条件的嵌入水印信息，其余像素相应联动，即

(5)

除了灰度直方图外，类似的图像统计类特征还很多，如可利用差值构建直方图完成修改(Tai等，2009)。若能结合特定的目标函数来指导直方图修改，不再仅仅局限于容量和失真这一对常规评价指标，则有望实现具备较好应用价值的算法。在理论推进方面，诸如，通过直方图嵌入框架研究(Li等人，2013a)2维直方图扩展研究(Li等人，2013c),结合率失真模型的方法(Wang等，2017)和结合通信码分复用的方法(Ma和Shi，2016)都是近期有代表性的工作。在实际应用方面，早期比较有代表性的算法有Huang等人(2011)和Jung等人(2011)在2维码和人眼视觉感知上的探索。

2 JPEG图像可逆信息隐藏回顾与发展

JPEG是当前应用最广泛的一种图像格式，与空域图像相比， JPEG 图像可逆信息隐藏区别在于：

1) JPEG 图像已经压缩，其数据冗余远少于未压缩格式图像，如何实施高效的可逆信息隐藏是一个颇具挑战性的任务；

2) JPEG 图像可逆信息隐藏易引起载体数据的增加，如何协调嵌入量、载体失真与载体数据扩展之间的关系是实际应用中必须考虑的问题；

3) JPEG 图像数据体现为离散余弦变换(discrete cosine transform, DCT)系数的熵编码形式，相关理论偏少，亟待进一步补充。

从理论、方法和应用等多层面、系统地开展 JPEG可逆信息隐藏研究，对推动可逆信息隐藏领域的均衡全面发展和实际应用具有重要意义。根据修改载体的不同，将现有的JPEG图像可逆信息隐藏方法分为修改DCT系数的方法和修改哈夫曼表的方法。

2.1 修改DCT系数的方法

根据嵌入算法的不同，修改DCT系数的方法可进一步被分为4类：1)基于无损压缩的方法；2)基于系数扩展的方法；3)基于零游程值(zero-run value，ZRV)对旋转的方法；4)基于直方图平移的方法。

2.1.1 基于无损压缩的方法

基于无损压缩的JPEG可逆信息隐藏方法由Fridrich等人(2002)首次提出。该方法基本嵌入过程如图1所示，通过语义无损压缩数字载体中的子集以腾出空间实现额外信息的嵌入。Fridrich等人(2002)选择将DCT块中部分中频系数的最低有效位(least significant bit， LSB)作为子集。该方法并未考虑DCT系数修改对文件大小造成的影响，导致修改后的图像文件大小膨胀明显。随后Fridrich等人(2004)提出了一种保持文件大小不变的方法。与Fridrich等人(2002)方法相比， Fridrich等人(2004)通过构造嵌入对来限制系数的选择和修改范围。同一系数对的系数值在修改前后编码长度不会发生变化，因此可以实现文件大小保持不变。Wang等人(2013)提出一种新的辅助信息构造方式以增大嵌入容量(其中，X为载体，X′为含密载体，B为原始码流，BC为压缩后的码流，M为待嵌入信息)。与Fridrich等人(2002，2004)直接压缩系数的LSB不同，Wang等人(2013)首先将交流系数的LSB设置为全0后，通过分析空域的像素块效应来从中重建原始的LSB，以实现更高的压缩率。

图1 基于无损压缩的可逆信息隐藏基本过程Fig.1 The framework of reversible data hiding method based on lossless compression

由于系数的LSB序列中0，1分布概率较为均匀，经无损压缩后可腾出空间有限，因此基于无损压缩的方法可获得的嵌入容量较低。

2.1.2 基于系数扩展的方法

2.1.3 基于ZRV对旋转的方法

基于ZRV对旋转的方法由Ong和Wong(2013)中首次提出。ZRV对是对AC系数采用游程编码得到的中间形式。该类方法将DCT块中ZRV对序列以顺逆时针的顺序进行旋转，得到若干状态的ZRV对序列，分别对应若干比特数据。因此可以通过旋转ZRV对序列以实现信息嵌入。Long等人(2016)取消对ZRV对分组，从而获得更高的嵌入容量。

基于ZRV对旋转的方法在信息嵌入过程中只修改ZRV对的排列顺序，对交流系数幅值并无修改，文件大小在信息嵌入前后不会发生明显改变。但信息嵌入后非零交流系数位置发生明显变化，会导致较高的视觉失真。此外，由于需要多个ZRV对来表示信息，该类方法实际得到的嵌入容量有限。

2.1.4 基于直方图平移的方法

基于直方图平移的方法通过将系数直方图峰值点外元素平移以制造零值点来实现信息嵌入。图2展示了直方图平移的基本嵌入过程。对于一个特定序列，首先确定其峰值点x，然后将峰值点右方的元素向右平移一个单位以腾出空间，嵌入时根据待嵌入信息将峰值点元素修改或保持不变。基于直方图修改的方法由于能提供更高嵌入容量，且具有良好的率失真性能和文件大小保持性能，近年来成为JPEG可逆信息隐藏研究的主流方法。

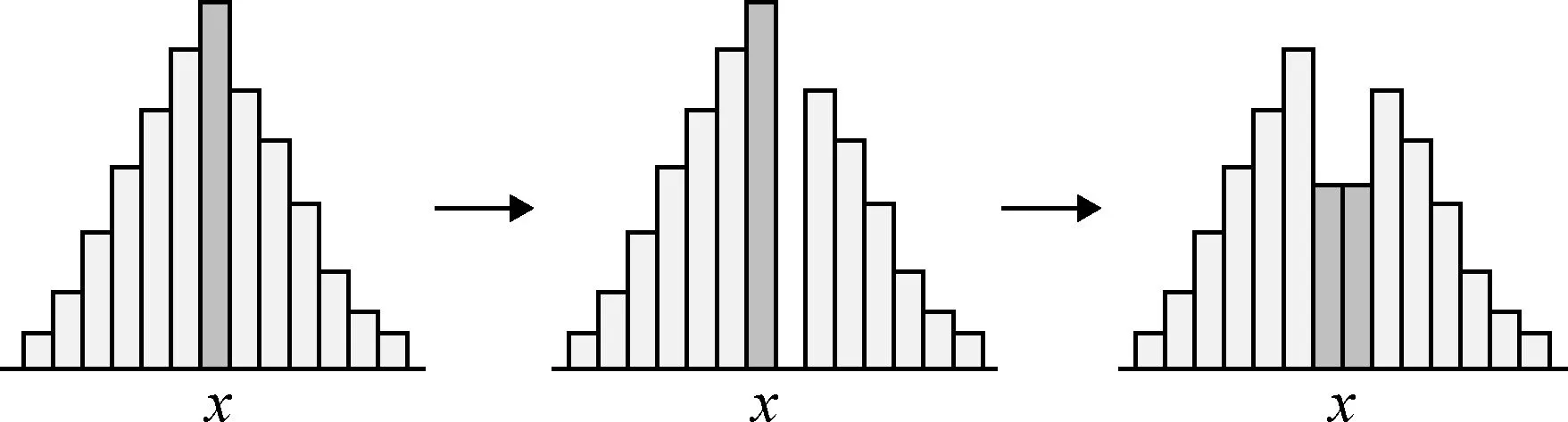
图2 基于直方图平移的嵌入过程Fig.2 The embedding procedure in HS

Xuan等人(2007)首次将直方图平移的嵌入思想应用到JPEG图像，提出基于直方图对的方法实现信息嵌入。在该方法中，根据所设阈值构造直方图对。为了保证直方图对中存在零值点，需要进行直方图扩展操作。构造完成后该直方图即可用于数据嵌入。为了提高嵌入容量，该方法可进行多轮嵌入。为了选择合适的阈值，Xuan等人(2007)还设计了最优参数搜索策略以确定最优的阈值。Sakai等人(2008)提出直方图扩展操作在纹理复杂区域相较于平滑区域引起更大失真，因此提出通过计算块中直流系数的方差来将其作为块排序依据，将附加信息优先嵌入到平滑块中以提高率失真性能。Xuan等人(2019)基于最小熵原则设计了一种块选择策略以减少视觉失真。Nikolaidi(2016)提出将绝对值大于阈值的系数向两边扩展以制造零值点用于信息嵌入。Huang等人(2016)提出修改直方图时保持零值交流系数不变，但只选取值为±1的交流系数作为峰值点用于携带附加信息。同时还提出一种新的块选择策略以减轻视觉失真：优先在零值交流系数个数多的块，也即平滑块中嵌入信息。Huang等人(2016)提出的方法为基于直方图修改的JPEG可逆信息隐藏研究注入新的活力。此后，相关改进工作层出不穷，主要集中在优化选择策略以及峰值点构造两方面：

1) 选择策略。选择策略包括块选择策略与频率选择策略，目的分别是优化DCT系数块间修改顺序和块内修改顺序。Qian等人(2017)提出一种排序嵌入策略，优先将信息嵌入到数量较少且相应零游程较短的块，有效降低了文件大小膨胀。Wedaj等人(2017)发现不同频率的系数中可供嵌入和只用来扩展的系数存在明显差异，对不同频率的交流系数修改造成的失真也不同，故提出通过计算每个频率的嵌入效率以用于排序。Hou等人(2018)提出计算不同频率的交流系数的单位失真，并计算其对应的模拟失真作为排序依据。嵌入时每个块只选择失真较小的部分交流系数来进行直方图修改，从而提高率失真性能。He等人(2020)基于DCT系数分布来估计块失真，将其作为块排序依据。上述方法提出的选择策略是从两个方面来设计优化目标，即尽可能保持文件大小或优化率失真性能。He等人(2019b)提出一种负影响模型，同时考虑两方面性能并根据实际需求，通过调整权重来兼顾两者。Yin等人(2020b)采用多目标优化算法将文件大小的变化与视觉失真同时纳入考量，从而提高综合性能，在Huang等人(2016)和Hou等人(2018)的工作上进一步验证了所提出的多目标优化算法的效果。王洋洋等人(2020)则提出一种新的联合度量标准即单位失真与增长比作为视觉质量与文件扩展关系的定量评价指标。

2) 峰值点构造。Yin等人(2017)使用K近邻算法自适应选择峰值点并优先将附加信息嵌入到非零交流系数少的块中以提升嵌入容量及视觉质量。Kim等人(2019)利用相邻块间的直流系数相关性较强的特点，建立对应的预测误差直方图并对其进行扩展以嵌入数据。Li和Huang(2020)提出一种基于成对非零交流系数的直方图扩展方法。通过将两个非零交流系数联合考虑，建立系数对直方图，并针对该直方图设计可逆2维映射。Xiao等人(2021)则提出使用多直方图修改嵌入框架并建立率失真模型以准确估计嵌入失真，同时采用贪婪算法以搜索最优解。

除上述方法外，Chen等人(2021)将非一致失真度量下的递归直方图修改方法与直方图平移结合，通过将绝对值大于2的DCT系数向两边平移以将值为±1、±2的系数作为载体序列，再使用递归直方图修改的方式实现信息嵌入。因为考虑了多种失真度量，Chen等人(2021)在视觉质量、文件大小膨胀甚至不可检测性上取得优异性能。

2.2 修改哈夫曼表的方法

修改哈夫曼表的方法也被称作无损信息隐藏方法。该类方法在信息嵌入前后只修改压缩数据流，不涉及对DCT系数的修改，所以解码后得到的图像内容与载体图像相比无失真。

修改哈夫曼表的方法利用JPEG压缩编码冗余，通过修改JPEG文件头中的哈夫曼表信息及压缩数据流实现信息嵌入。在JPEG图像中，标准哈夫曼码表构造的编码空间常有剩余。基于该特点，Mobasseri等人(2010)提出一种基于变长编码(variable length code, VLC)映射的方法，通过翻转已使用编码的若干比特来构造编码映射关系。然而，在重映射过程中，一些附加位信息可能会被修改，导致含密图像的视觉质量受到影响。为此，Qian和Zhang(2012)在构造映射关系时不再修改附加位，而是为已使用编码分配若干未使用的编码来建立映射关系，使含密图像无视觉失真。为保持嵌入数据后的文件大小不变，同一映射集中已使用编码与未使用编码长度需保持一致。图3展示了基于VLC映射的信息嵌入示例。

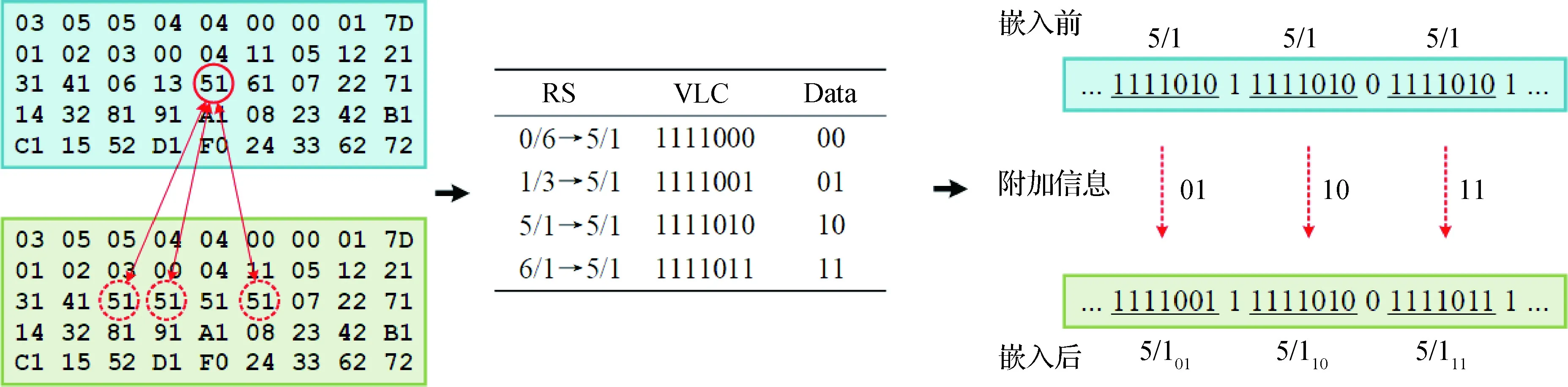
图3 基于VLC映射的无损嵌入示例Fig.3 Example of VLC-based lossless data embedding

Hu等人(2013)利用已使用VLC的频率信息，在构造映射关系时将更多的未使用VLC优先分配给高频已使用VLC，以提高嵌入容量。Qiu等人(2018)还将VLC映射与重排序方法结合，通过混洗原始哈夫曼码表中定义的编码顺序，进一步提高嵌入容量。Zhang等人(2020b)充分考虑了VLC每种组合的可行解以建立最优映射关系。为了降低算法计算复杂度，Zhang等人(2020a)还提出了一种参数优化方案以重新定义优化目标并精简解空间。

因Qian和Zhang(2012)、Hu等人(2013)、Qiu等人(2018)和Zhang等人(2020a)需要满足嵌入后文件大小保持不变，因此实际获得嵌入容量有限。在允许文件大小有一定增长的条件下，对嵌入率和文件大小保持性能的探索更具实用意义。对此，Qiu等人(2021)中提出结合不同长度VLC的中继移位算法，在有效控制文件大小增量的前提下，嵌入容量获得显著提升。Du等人(2020)则将VLC映射与多直方图平移技术结合实现高嵌入容量，同时建立模拟嵌入模型用于选择最优的映射组合以抑制文件大小增长，所提方法的文件大小保持性能优于一些最新的修改DCT系数的工作，如Qian等人(2017)、Wedaj等人(2017)和Hou等人(2018)。Zhang等人(2020b)考虑了优化文件大小的增加，通过使用概率转移矩阵以模拟理论模型并设计优化规则以构建更优的VLC映射关系。

尽管Qiu等人(2021)、Du等人(2020)和Zhang等人(2020b)在嵌入容量和文件大小保持性能方面与目前其他JPEG可逆信息隐藏方法相比达到了领先水平，但仍存在适用性的问题亟待解决。具体来说，该类方法只适用采用标准哈夫曼表压缩得到的JPEG图像，不适用采用优化哈夫曼表压缩的JPEG图像。因为优化后的哈夫曼表考虑了图像自身分布特性，表中定义的编码在实际编码中均被利用，所以无法直接构建映射关系。Yin等人(2020a)中利用游程大小值的分布特性来构造映射关系，根据给定嵌入率分配不同数量的编码，从而将编码映射形式化为组合优化问题并采用遗传算法求解。不管原始JPEG图像采用何种哈夫曼表压缩得来，映射关系都可以正常构建，因此适用性问题得到解决。同时文件大小保持性能也相较于Du等人(2020)有了进一步改善，其性能领先于基于修改DCT系数的方法(He等，2019b；Li和Huang，2020)。

除此之外，近年来也有一些针对密文域JPEG图像的工作(Qian等，2014，2018，2019；Yin等，2018；戴禹和殷赵霞，2018；He等，2019a)。

3 可逆鲁棒水印回顾与发展

载体无损鲁棒水印技术是信息隐藏研究领域中的前沿热点之一。该技术同时具备可逆性和鲁棒性的优点，在未受攻击时可以提取水印并无损恢复原始载体；当遭受一定程度攻击时则以放弃载体恢复为代价，保证提取出水印信息的正确性，来认证数字媒体内容。同传统的鲁棒水印技术相比，该技术在发送端和接收端都具有明显的优点：

1) 在发送端，所有者无需担心因水印嵌入会造成载体永久失真，在存储时也可只保留嵌入水印的文件，在应用的广度和深度上更好。

2) 在接收端、无攻击情况下，合法用户可从含水印文件直接恢复出原始载体，避免重新发送原始文件，在应用上更加方便。

近年来，国内外的研究者已做了一些初步的相关研究工作，根据嵌入策略的不同，主要可以分为以下两类。

3.1 基于直方图平移的载体无损鲁棒水印技术

基于直方图平移的载体无损鲁棒水印技术(Gao和Shi，2015，)也称鲁棒可逆水印技术，主要用于数字媒体内容的半脆弱认证。该技术的水印嵌入示意图如图4所示。整个水印嵌入过程主要由两个步骤组成：1)选取鲁棒特征并构建鲁棒特征的直方图，如图4(a)所示；2)平移直方图以嵌入水印并产生鲁棒区，如图4(b)所示。可以看出，在完成水印嵌入后，比特1区与比特0区之间存在鲁棒区G。因此，即使含水印的载体遭到一定程度的攻击，若鲁棒特征没有因为攻击而落入错误的比特区中，水印仍然可以被正确地提取出来。基于直方图平移的载体无损鲁棒水印技术最早由Ni等人(2008)提出，后续得到了进一步发展(Gao等，2011；Zeng等，2010；Liang和Xiang，2020)。基于直方图平移技术方案的优点是容量比较大，可以有效地对抗有损压缩、滤波以及高斯噪声等常规信号处理操作。

图4 基于直方图平移的载体无损鲁棒水印技术Fig.4 Histogram-based robust reversible watermarking method

3.2 基于二阶段嵌入策略的载体无损鲁棒水印技术

基于二阶段嵌入策略的载体无损鲁棒水印技术最早由Coltuc和Chassery(2007b)提出，主要思想是将水印的嵌入过程分为两个阶段(如图5所示)：在第1阶段中进行鲁棒水印的嵌入；在第2阶段将鲁棒嵌入时产生的失真作为补偿信息进行可逆嵌入，从而实现载体无损。考虑到在空域可逆嵌入补偿信息可能会降低水印的鲁棒性， Wang等人(2020)通过哈尔小波变换将水印信息嵌入到低频子带来实现对JPEG压缩等常规操作的鲁棒性；将水印在低频组件的嵌入失真作为补偿信息可逆嵌入到高频子带来实现载体可无损恢复的目的。为了对抗旋转、拉伸和平移等几何失真， Hu和Xiang(2021b)分别利用低阶Zernike 矩和极弦变换来实现鲁棒水印的嵌入，进而通过优化减小补偿信息并嵌入来实现可逆。这两个方法不仅对有损压缩等常规信号处理具备鲁棒性，也可以有效对抗旋转和拉伸等几何失真。

图5 基于二阶段嵌入策略的载体无损鲁棒水印技术(M为图像因鲁棒嵌入产生的变化量)Fig.5 Robust reversible watermarking based on two-stage embedding strategy, where M denote the changes on the image after the robust embedding

基于二阶段嵌入的载体无损鲁棒水印技术可以充分利用鲁棒水印技术的优点，并借助可逆水印方法来实现了载体无损。由于可以将水印嵌入到图像或音频的鲁棒特征(如低频系数，几何不变矩等)来对抗常规信号处理和几何攻击，具有嵌入灵活、鲁棒性好的优点。目前，对载体无损鲁棒水印技术的研究仍处在初期阶段，现有算法在嵌入容量、不可感知性以及鲁棒性等方面仍有待改进。关于未来的研究方向，有以下3点思考：

1) 如何构建与位置无关的鲁棒统计特征，从而设计出无需二次嵌入补偿信息、可抗几何攻击的载体无损鲁棒水印算法；

2) 如何在多时域或变换域中考虑JPEG图像、MP3文件等使用的普遍性，实现载体无损鲁棒水印算法；

3) 载体无损鲁棒水印技术需要考虑可逆性、鲁棒性、嵌入容量和不可察觉性四者之间的平衡，目前尚缺少理论基础模型的支撑。

4 思考与展望

当前，社会正在进入认知计算时代，即计算机在某些特定方面逐步获得了接近于人的智力。在计算智能时代，可逆研究要融合当前先进的认知计算能力，首要任务是转化传统的可逆优化问题为计算机可以理解的方式，同时将可逆嵌入提取的行为模式也转化为认知计算可以量化的单元，尤其是过去经典的、成功算法的行为模式。在此基础上，利用深度学习、强化学习等多层次、大运量的计算，去加速和改进过去人为寻优的传统方式。以此为切入点是初期可行的路径。随后，在迁移过程中去发现的新问题和矛盾，然后设计真正全新的算法。显然，新问题的提出、特定应用问题如何描述、从无到有的新方案设计是不能依赖计算机去完成的，创新的问题只能依靠人来完成。这留给研究者以足够的发挥空间。如能结合认知计算能力，让重复性的、验证性的工作交由计算机，人则有余力去探索更新的领域，可逆研究的应用面就会扩大。

对于现有的可逆算法，研究目标似乎也可随时代略微调整。过去可逆水印一直强调载体完全无失真的恢复，但实际评价好坏的主体始终是人。数字上完全精确的复原，对于人而言并非必要。实际上，人无法感知特别细微的变化，那么完全实现无失真恢复似无必要。实事求是地说，数字图像本身就是自然景象的一定程度失真后的反映，人依然可以在此“失真”的载体上做出正确判断和使用。那么在医学、司法等领域，是否保证图像大体恢复，接受微小的失真也合理？这值得讨论探索。如果把过去的可逆信息隐藏称之为完全可逆，那么不妨把实现大体可逆的算法叫做深度可逆。在此概念下，则不必图像的所有区域完全可逆恢复，又或者不必每个像素在恢复后完全没有失真。嵌入的信息也不必再是版权保护的水印，可以为其它满足特定需求的信息。若可行，可逆设计的方法就会灵活得多，弹性得多，适用范围也必然广泛得多。其实，完美的可逆恢复本身要求就接近苛刻，必然只能局限于极个别的领域，是小众的。而深度可逆能使用的场景将会十分丰富，是大众化的。

除此之外，经典可逆理论在新时代下也并未丧失活力，其潜在新应用依然不少，较为典型的应用方向(Hou等，2019)包括：

2)可逆隐写。该技术只是微小地嵌入信息到载体之中，来大幅提升可逆嵌入的安全性。因为修改变少，嵌入位置和规则都不必沿用传统可逆框架，不受传统限制而灵活很多。若将隐写看成是进攻的手段，可逆性则是将进攻所造成的自我损失尽量减少的弥补方式。在网络安全攻防日益被重视的今天，此研究的产出值得期待。

4)可逆图像处理。该技术可以用可逆嵌入的方式去模拟常规的图像处理操作，在完成特定信息嵌入的同时又能实现所要求的图像处理。如对比度增强，本质上就是直方图均衡的过程，可逆嵌入完全可以模拟此操作。这样，在完成可逆嵌入的同时，也完成了所需的图像处理操作。相关研究已经由Wu等人(2015)率先提出。

5 结语

可逆信息隐藏是一项用于图像恢复和水印提取的特殊技术，在现今强调信息价值的时代，有着很强的潜在应用价值。可逆信息隐藏的独特之处在于能够一定程度地恢复图像初始状态，因而在敏感领域的图像处理中率先应用。当然，这种针对图像的恢复、溯源能力也使其能够兼容大多数应用需求，从而发挥很强的辅助促进作用。可逆研究已近三十年，相比于初创时的环境，形势已经发生很多变化，先有所取舍，再有所发展，势在必行。若能回应时代热点需求，解决更难、更广泛的问题，才能长远发展。