立足课本 渗透素养——2021年安徽省数学中考第23题简析

刘清清

(上派初级中学，安徽 合肥 231200)

每逢中考季，关于中考分析的文章处处可见，从文章的篇数反映出中考试题的无穷魅力，而不同的写作角度折射出中考试题立意绵长，2021年安徽省数学中考的试题亦是如此.

1 试题回顾

例1如图1，在四边形ABCD中，∠ABC=∠BCD，点E在边BC上，且AE∥CD，DE∥AB.作CF∥AD交线段AE于点F，联结BF.

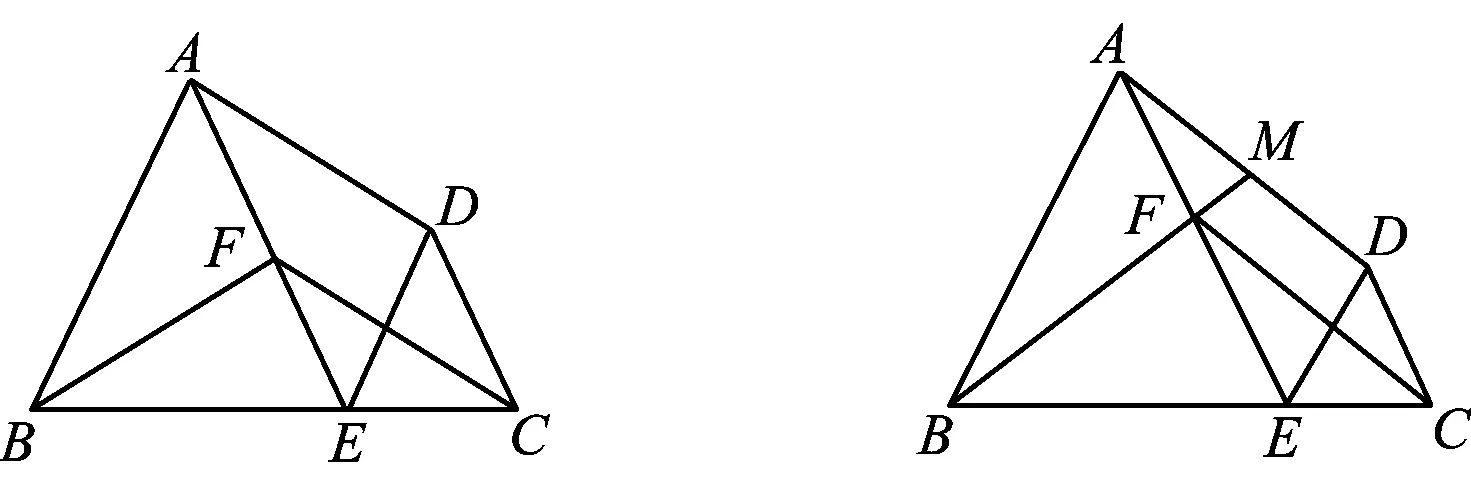
图1 图2

1)求证：△ABF≌△EAD；

2)若AB=9,CD=5,∠ECF=∠AED，求BE的长；

(2021年安徽省数学中考试题第23题)

2 试题简析

从图形的复杂程度来看，该题的图形可谓简洁清晰，没有“盘根错节”之感，更没有让人眼花缭乱的题干信息.考生审题、读图后的感受可谓清清爽爽，命题者力图让考生在感官上进行舒压，可见用心良苦和至简之心，展现了命题者的人文关怀和命题温度.

2.1 追根溯源

2021年3月18日，在安徽合肥举行的九年级复习研讨吹风会上就明确提出，复习时要紧扣课本，夯实基础，在课本的基础上适时、适当、适度地进行延拓与发散，不能忽视课本的本源性.“丢弃课本，一味追求题目的训练是不可取的，是错误的走向”，最终引导学生走出复习的误区.因此，此次吹风会让一线教师找到了复习的方向和最佳的复习教材——课本.那么，例1的“根”扎在课本何处呢？又“长”到哪里呢？

2.2 扎根课本

首先对题干信息进行简单地分析，便可迅速地得到△ABE和△DEC均是等腰三角形，且这个图形在沪科版《数学》八年级上册学习等腰三角形时可谓“司空见惯”.习题15.3中的第12题是这样描述的：

如图3，点C是线段AB上一点，△ACM和△CBN是等边三角形，AN交CM于点E，BM交CN于点F.求证：

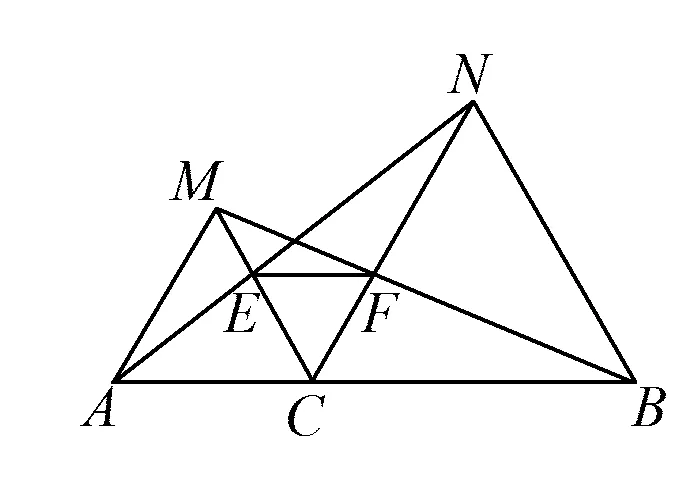
图3

1)CE=CF;

2)EF∥AB.

该题的已知条件“等边三角形”有点“完美”.正是因为过于“完美”的已知，锐减了本题的难度，缩短了思考的进程，降低了思维的维度.然而，这正是图1能够在此基础上进行改编的前提.

对比图1与图3，图1可以轻易地得到两个等腰三角形，图3是已知两个等边三角形，而等边三角形是等腰三角形的特殊情形.现在，我们探析图3，由于△ACM和△CBN是等边三角形，因此AM∥CN，CM∥BN.而在图1中，题目中用“∠ABC=∠BCD，且AE∥CD，DE∥AB.作CF∥AD”替代了“等边三角形”这个条件.二者相比较，命题者在拔高课本基本图形的同时进行逆向思考，将课本题目的已知条件进行适时变换，将图形进行适当调整，体现了“扎根课本，依托课本”的初心.回到课本的图3，通过日常的教学研讨可以发现，教师在讲解本题时，通过简单讲解和拓展，将题目变式为“如图3，△ACM和△CBN是等腰三角形，且AM∥CN，求证：AN=BM”.这样变式的目的有3个：一是为了巩固刚刚学习的等腰三角形；二是回顾平行线的性质；三是全等三角形的应用.无论是变式还是图1，课本中的图3就是原始图形；无论是变式还是图1，其解决办法均要用到全等三角形.如此综合来看，三者看似千丝万缕，最终殊途同归，再次说明了命题者“紧扣课本”的初衷.

2.3 回望往昔

上面一段主要简析了例1的图形在课本中的原型.从考题的解答形式，看是否有往年中考题的身影呢？首先从例1的论证(求解)形式来看，第1)小题是证明三角形全等，第2)小题是求线段的长度，第3)小题是求线段的比值.翻阅安徽省历年数学中考真题，2015年安徽省数学中考第23题是这样描述的：

例2如图4，点A,B分别在射线OM，ON上，且∠MON为钝角.现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点.

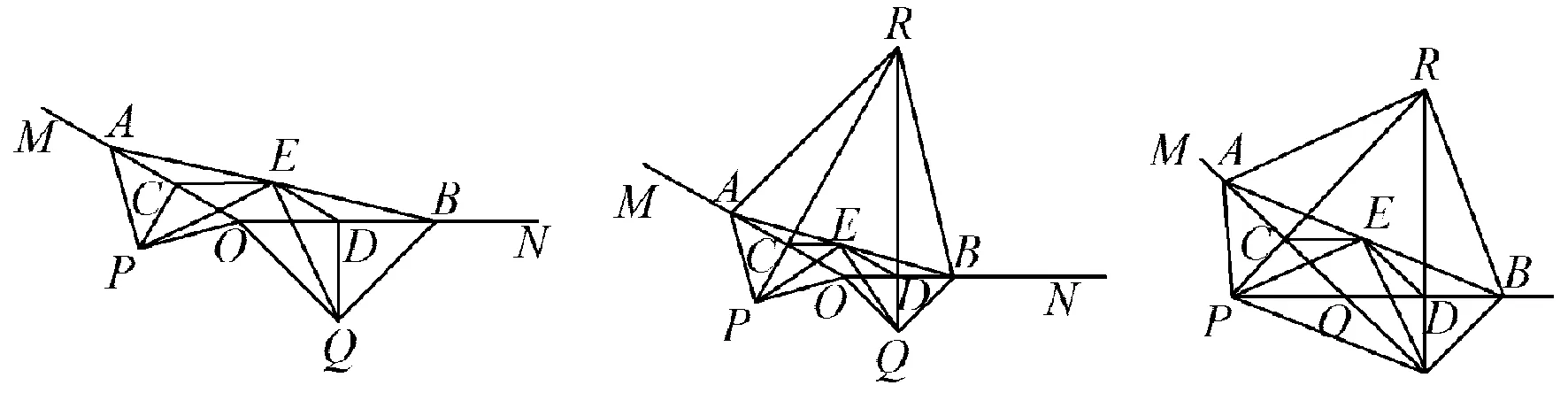
图4 图5 图6

1)求证：△PCE≌△EDQ.

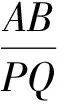
(2015年安徽省数学中考试题第23题)

从设问的结构上看，例1和例2有极大的相似之处，二者的第1)小题均是证明全等三角形，第2)小题或求线段的长度或求证等边三角形，第3)小题是线段的比值.极度相似的设问给予学生记忆上的“熟悉感”，消除紧张心理.再从二者的证明方法上看，也有共同之处，特别是第3)小题的解决方法上，例1和例2均是设某条线段的长度为单位1，从而由前两问得到启发，计算出线段的比值.

就第23题而言，2021年的题目胜于2015年的.首先，从图形的简洁性上看，2015年的图犹如迷宫，线段的走向也是错综复杂，让考生“望而生畏”.在紧张的环境中，困住考生的不是试题的难度，而是视觉的冲击造就了消极的心理暗示.2021年的考题，图形简洁，图形的轮廓了然于心，这无疑给学生传达出积极的心理暗号——静心答题，必有所成.接着从试题的已知条件上看，二者均是在等腰三角形的大背景下进行改编，而且二者均加入了角度相等或角的度数，让试题的内容更加丰富和多元.从这个层面上来看，二者不分伯仲.最后，从第3)小题的解题过程来看，例1的解题之路更为艰难.因为仅仅设CE=1是不够的，还需要假设BE=x,DC=a,先根据△MAB≌△MDG，再根据△FAB∽△FEG得到关于x的一元二次方程，最后求解x即可.从上面的简述过程可以看出，考生在解答时需要考虑3个变量，还要关注变量之间的数量关系，难度高于例2.因此，例1是例2的再提升、再创造.

2.4 变式拓展

3 教学启示

如果说中考试题的解法分析是发散思维、开拓思考的路径，那么中考试题带来的教学启示就是让思维有发散的源头，让开拓路径的基础更为坚实.例1又蕴涵着怎样的教学启示呢？

3.1 知识跨度，关注整体结构

例1的题干信息中有4个已知条件，其中3个都是关于平行线的.以沪科版《数学》为例，平行线的知识属于七年级下册内容，由已知信息导出的等腰三角形和证明全等三角形是八年级上册的内容，到根据需要证明平行四边形(八年级下册内容)，从七年级到八年级的横向跨度，显示出关注课本知识结构的设置，以及知识的螺旋式上升，这既符合学生分析问题的一般规律，也符合试题对综合能力的考查意图：需要学生前后联系七、八年级的相关知识，建立起有效的知识联结，进而快速解题.第2)小题相似三角形(《数学》九年级上册内容)，试题渐进式的设问体现了考生获取课本知识的先后顺序，思维量也随之增加.同时第2)小题追加了对计算能力的考量，这也为后面的第3)小题埋下了伏笔.

3.2 数学运算，关注学科核心素养

一年一度的中考测试，不仅是为了测试学生的“四基”“四能”，更是检测考生是否适合继续进行高中学习的依据之一.《普通高中数学课程标准(2017年版)》中明确提出数学学科素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的.在六大核心素养中，数学运算位列其中.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，是解决数学问题的基本手段，而数学运算是演绎推理，是计算机解决问题的基础[1].因此数学运算在高中三年的学习过程中展现得淋漓尽致，可谓“计算正确得天下”！如何将这讯号传递到初中阶段，引起初中学生的足够重视呢？将数学运算的思想渗透到中考考题中无疑是最好的选择.例1的第3)小题将数学运算糅合在平面几何的演绎推理中，将运算与推理巧妙地结合，既考查了学生的全等三角形、相似三角形的应用能力，又考查了学生的数学运算能力，也为研究中考试题的教师们指明了复习的方向和重点，一箭三雕可谓精妙.

初中阶段是小学阶段的延续，是向高中阶段过渡的关键时期，因此养好良好的思维品质是初中阶段学习的重要任务.然而通过笔者参加中考阅卷的经历来看，数学运算仍是考生失分的重要原因，培养学生的数学运算素养任重而道远.当前的复习教辅资料铺天盖地，良莠不齐，教师也难以抉择，例1给一线教师提供了最佳的复习材料——课本.在紧扣课本的同时，需要教师沉心静气，钻研课本，对课本上的图形进行适度的改编.只有考生“啃”透课本，才能以不变应万变.