基于单元统整的章起始课教学实践探索——以人教版“实数”为例

邢成云

(北镇中学实验初中部，山东 滨州 256609)

时下，单元整体化教学备受关注，这也是笔者从教以来的探索研究，目前已形成了基于课程统整之上的整体化教学主张[1]，其实这也是新的课程改革强调整体把握课程的大势所趋.但理念愿景与现实行动之间往往有距离，因此理念如何真正落地才是关键.笔者在教学中主张对“章起始课”进行探索，较好地解决了这一问题.现以人教版初中《数学》第6章“实数”为例，展示章起始课的设计历程，与诸位同仁共享.

1 通观资源，整体规划

1.1 对章前语、章头图的认识

两段文字一个图，文图呼应.第一段文字通过创设科学情景，引出了一个数学问题，即如何知道二次幂求底数的模型，揭开了本章的核心问题；第二段文字通过单位正方形获得对角线的长度问题，这个长度数值不是有理数，而是相克而生的一类数——无理数，由此数系扩展为实数，然后通过类比有理数引入实数在数轴上的表示及其运算，并用之解决实际问题.而章头图是火箭发射图，呼应了第一段文字的科学情境.总之，章前语、章头图共同把本章的核心内容以及研究思路摆了出来，为章起始课的设计提供了统摄性材料.

1.2 立足课标，解读教材

课标中对应本章课程内容：

1)了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根、算术平方根、立方根;

2)了解乘方与开方互为逆运算，会用平方运算求百以内整数的平方根，会用立方运算求百以内整数(对应的负整数)的立方根，会用计算器求平方根和立方根;

3)了解无理数和实数的概念，知道实数与数轴上的点一一对应，能求实数的相反数与绝对值;

4)能用有理数估计一个无理数的大致范围(可参见文献[2]中的例47，此处略);

5)了解近似数，在解决实际问题中，能用计算器进行近似计算，并会按问题的要求对结果取近似值；

6)了解二次根式、最简二次根式的概念，了解二次根式(根号下仅限于数)加、减、乘、除运算法则，会用它们进行简单的四则运算(可参见文献[2]中的例48).

在无理式退出义务教育教材后，二次根式被划进了实数大范围，这一大范围在现行的人教版教材中被分化为两章：一是七年级下册的“实数”；二是八年级下册的“二次根式”.作为七年级下册的“实数”，其学习目标是前5条(见前文)，第6条是二次根式的学习目标.

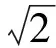
以上内容不仅是后面学习二次根式、一元二次方程以及解三角形等知识的基础，也为高中数学中学习不等式、函数以及解析几何等大部分知识做好“四基”的储备.

1.3 育人价值分析

1.4 整体规划单元学程

第一课时是章起始课.整体统摄，勾勒出本章的结构图(把教材的章前语、“阅读与思考”融入).

第二课时是顺承巩固课.在章起始课的基础上，进一步认识平方根、立方根以及算术平方根等概念及简单运算(把教材“活动1”融入，布置为课后作业，实现动手与动脑的结合).

第三课时是深度探研课.在章起始课的基础上，深化认识无理数、实数等概念，以有理数运算为基础，同构实数运算，感知数的发展历程，形成对实数的深入认识.

第四课时是小结统合课.本节课是对本章的二次统整，立足教材小结，形成完善的知识结构，从而提高学生整理知识、反思建构的学习力(把教材活动2融入，布置为课后选作作业，给有兴趣的学生以思维进阶的机会).

第五课时是分层考查课.分A,B,C三层级设立评价题目，形成AB,BC两个组合，由学生自选进行测试，其中A对应教材的拓广探索题，B对应教材的综合运用题，C对应教材的复习巩固题.B是保底评价题目，A,C两组题等分值设计.

根据“单元—课时”设计，本节起始课即为单元设计中的第一课时.

2 立足起始，整体统摄

2.1 教学目标

1)利用逆运算，获得平方根的概念，进而认识其基本性质，在此基础上获得算术平方根，会用根号表示，并了解算术平方根的非负性，明晰算术平方根与平方根的种属关系；

2)通过类比获得立方根的概念及有关性质；

4)通过渐成性板书勾勒出本章的知识概貌，形成整体研究路径.

2.2 教学重难点

重点：平方根(算术平方根)的概念及单元统摄结构的形成.

难点：平方根概念的获得以及对无理数的初步认识.

2.3 教学过程设计

环节1起于拼图.

问题1用两张面积为1的正方形纸片，能否通过有限次的剪切、拼接，拼出无缝隙的新正方形，用图示展示自己的拼法，并说明为什么能实现拼接.

教学说明事先安排学生课前先行尝试，动手拼图，课堂上用来展示与交流理由，以感知面积等于2的正方形边长的客观存在性.

学生展示两类拼图(如图1和图2所示)，引出关系式x2=2.

图1 图2

设计意图面积、体积是平方根、立方根的依附载体，正方形的面积、立方体的体积是平方、立方的可感质体，是数与形结合的有效介质，这为学生拼图的可行性奠定了基础，让平方的逆运算有了可感的元素.基于此，利用教材中第41页的拼图作为先行组织者，把核心问题揭示出来.

环节2成于互逆.

问题2章前语中第一段提出的问题以及环节1中的拼图形成的关系可抽象为x2=m的形式，这里m是已知的，求x的取值.由此我们联想到以前是怎么处理的？

教学说明通过一组填空唤起学生用逆运算研究的想法，然后引导学生回顾学过的逆运算：

-3+(12)=9， -3×(-3)=9，

-3+( )=9， -3×( )=9.

加减互逆：a+b=c→a=c-b，b=c-a.

顺势出示(-3)2=9与( )2=9，在师生问答中提出问题3.

问题3加法与减法互为逆运算，乘法与除法也互为逆运算.那么“已知指数2与幂m，求底数x”是什么运算呢？它和平方运算有什么关系呢？

预设由此又会出现一种新的运算叫开平方运算，结果叫平方根或二次方根，它与平方运算是互逆关系.

设计说明利用逆运算(类比加减互逆、乘除互逆)，引出新的运算——开平方运算(其本质就是求形式最简单的一元二次方程的根，故称之为二次方根或平方根).

问题4请同学们通过尝试活动及对互逆的认识，试着给出二次方根的定义.

预设一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，也称为二次方根(板书概念).求一个数a的平方根的运算，叫做开平方.

为拓展数的开方运算为式的开方运算，根据学情，若学生整体水平较高，则可增加一组练习如下：

1)求方程x2=4中x的值；

2)请观察下列方程，它们是怎样由方程x2=4逐步转化的：x2-4=0，(x-2)2-4=0，2(x-2)2-8=0；

设计说明本弹性环节既是拓展应用，又为解方程做铺垫.其中第1)小题是回归定义求解，第2)小题是以第1)小题为基础一步一步落实转化的，在化归中获得解方程的基本思路，第3)小题是通过第2)小题获得新发现并学以致用.

合作活动生生互助：一位学生给出一个数，另一位学生给出其平方根.

预设通过这样的开放性活动，学生会发现：4,9,16等的平方根均有两个，而2,5,6,7等的平方根没法写出来，-4,-16等的平方根又找不到，0的平方根只有一个……

至此提出问题5.

问题5学过的所有数是否都具有平方根呢？在求一个数的平方根的过程中会遇到哪些情况？

以上活动充分暴露了一个数的平方根的各类情况，通过追问和追问之下学生的探索，平方根的性质已成型，教师可以与学生一起归纳出平方根的性质(教师板书，学生默记)：

1)一个正数有两个平方根，它们互为相反数；

2)0有一个平方根，它是0本身；

3)负数没有平方根.

问题6通过学生互助活动，已经对平方根的性质有了一定的认识.但在活动中，也遇到了像2,5,6,7,11等数的平方根感觉有但又说不出来的问题，怎么办？

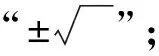
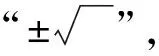
问题7关于平方根，我们研究了哪些内容？请同学们多角度地谈谈对平方根的认识？

预设从平方根的定义、性质、与方程的关系、运算(逆运算)、符号、应用等角度切入.

设计说明学生在七年级上册已学习了加、减、乘、除、乘方运算，积累了加和减、乘和除相互间存在互逆关系的数学活动经验.本环节基于学生的已有知识和已有经验，研究了平方的逆运算，即开平方，为后继环节立方根的学习搭起了框架结构，它在教学内容上起着统摄统领、承上启下的作用.

至此，思维启动起来了，如果就此打住，就失去了思维进阶的机会，由此，教师提出了问题8.

环节3发于类比.

问题8我们在学习数的平方后，还学习了立方以及乘方，体现了从特殊到一般的思想方法.类似地，在学完平方根后，还可以进一步研究什么？

预设研究立方的逆运算以及一般性的乘方的逆运算.如果一个数x的立方等于a，那么x叫a的什么？如果一个数x的四次方及n次方等于a，那么x叫a的什么？……由此引出立方根、四次方根及一般意义上的方根(n次方根).

相对应，立方与开立方也互为逆运算，即乘方与开方互为逆运算.

设计说明通过类比，获得开立方运算的结果称为立方根，进而提出n次方根的概念，但限于学段认知，n次方根将在高中阶段进一步学习，在此不展开，点到为止，只是为了实现从平方根到n次方根的贯通，体现前后一致性.初中阶段仅研究偶次方根和奇次方根的两个代表：平方根和立方根.这样从特殊到一般的研究思路呈现出来，不但扩充了知识，更重要的是拓展了思维，这是基于素养、着眼发展的好举措.

问题9根据刚才平方根的学习经验，同学们认为可以如何研究立方根？请同学们设想立方根的学习思路.

预设类比平方根的学习，我们需要研究立方根的定义、开立方的定义、立方根的性质、与方程的关系、立方根的符号表示、立方根的应用等.

设计说明充分利用平方根教学过程所形成的大思路、大框架，引领出立方根的学习脉络，并共同服务于大概念的教学——乘方与开方运算的互逆性.一个是教结构，另一个是用结构，它们逻辑连贯、一脉相承地彰显出来，其迁移性能得以展现，这就是单元教学的价值所在.

问题10请同学们从不同的角度谈谈对立方根的理解以及平方根、立方根的区别与联系.

预设略.

设计说明对比平方根和立方根的异同点，概括二者的相同点是一种同化过程，而理清二者的区别却是一种分化活动.分化的过程促进了学生对概念的理解，便于学生将新概念纳入已有的认知结构中，加深对新、旧知识的联系，优化知识在大脑中的储存和提取.

环节4终于内需.

预设讨论后指导学生阅读人教版七年级下册教材第58页的“阅读与思考”，初步感知无理数.或通过梳理数的发展历程的思路(再现数的逻辑发展历程：用微视频展播)，然后对照这4个数，发现它们不属于前面学习的各类数，那么它们到底属于哪类数呢？

由此，新的一类数出场的必要性突显出来，这类数的价值性不用多言，顺理成章，意义建构，有理数、无理数携手出场，实数的概念水到渠成.至此，本章的概貌基本形成.

环节5收于小结.

基于渐进性板书，知识系统的结构图水到渠成，通过完善板书终成概貌.

图3

设计说明结构图不仅仅是知识的组合，更是建立了一种知识点之间的内在结构，既可以展现学习的路径，也能表达数学概念学习的一般套路.这是对策略性知识的渗透，也是一种着眼于学生会学的行动.

3 教学反思

3.1 重构中厘清脉络

现行人教版教材的设计是把算术平方根设置为第一课时，然后才是平方根，随后是立方根，最后是实数的学习，这个脉络也体现了知识学习的基本路径.但笔者认为，作为具有统领性的章起始课，需要把本章学习的脉络厘清，让学生能见到“森林”，让知识之间的整体关联更加密切.基于此，笔者对教材进行了解构再统合，首先研究平方根，然后学习其中的特殊一族也是关键一族——算术平方根，如此，它们之间的一般与特殊的关系会愈加清晰，在此基础上学习立方根将不成问题，就在这样的研究过程中，不同于有理数的一类“数”登堂入室就水到渠成了.

3.2 互逆中见诸生长

平方与平方根、立方与立方根，相逆而生，代数中逆运算的构建、几何中逆命题的探索均是发现问题、提出问题的元认知性策略的践行.追溯旧知寻源头，逻辑发展即生长，是一种由内(基于数学的内部发展)而外的生成性学习，是对运算的自我完善，面对加、减、乘、除、乘方运算的发展，在加减互逆、乘除互逆已有现实经验的支持下，基于内部自洽，自然留下一个思维缺口——乘方是否有逆运算的构想.当然这样的思考也是基于前4种运算一致性的认识，是“大概念引领，大任务驱动”[3]，是整体观统摄、整体中孕育一贯、完善运算的行动.有了这种从逆运算角度引入新运算而完备知识系统的全息认识，使得教学更加自然顺畅，更加顺乎其然，展现出数学的本色.

3.3 类比中一脉相承

当平方根的学习落地后，类比平方根的研究思路自然获得立方根的系列知识，这是基于一致性的落实，就是把平方根的研究思路(吴亚萍教授的“教结构”)迁移到立方根的教学中来(用结构).如此，不但是借了力，降低了学生的认知负荷，简缩了探研时间，而且引导学生从学会走向了会学，真正落实了“教为主导、学为主体”的基本原则，在这样的一脉中加强了知识的逻辑连贯，章起始课的系统性、结构性、整体性跃然纸上.