挖掘例题价值 优化例题教学——以浙教版数学教材中的一道例题为例

赵妙妙

(浙江大学教育学院附属学校，浙江 杭州 31000)

例题是数学教科书的重要组成部分．李善良博士指出：“教材中的素材要坚持4个字，即精、典、新、思．尤其是数学教材中的例题、练习、习题，必须考虑学生的学习心理规律，根据数学运用的不同层次：辨认识别、变式练习、解决简单问题、解决复杂问题等，选配比较典型的题目，内部自成系统，相互联系，学生经过这些基本的训练足以掌握相关知识与技能，并且这些习题的量是最小的．”可见数学教科书中的例题是编者精心选编的，具有基础性、典型性、层次性、发展性和系统性等诸多特点．这就要求教师在教学的过程中，注重教材例题，深入研究教材，挖掘隐含在教材中的数学思想和潜在价值，培养学生的数学思维品质．

怎样才能更好地发挥课本例题的价值呢？我们知道数学知识不是零散的点，而是由点到面的系统知识．因此在进行例题教学时，要注意将数学基础知识进行有机地整合，使例题“活”起来．本文以浙教版《数学》八年级下册第5.2节“菱形”中的例2为例，谈谈笔者对例题教学的一点思考．

1 课本例题的呈现及思考

例1如图1，在矩形ABCD中，对角线AC的垂直平分线与边AD，BC分别交于点E，F，求证：四边形AFCE是菱形．

本题重点考查菱形的判定．虽然教材中只展示了一种证法，但是在例题教学中，恰当且适量地采用“一题多解”教学，进行多角度的解题思路分析，对学生巩固基础知识、提高解题技能、发展逻辑思维、提高分析问题和解决问题的能力十分有益[1].

本题主要有以下几种证明思路：

思路1定义法，即一组邻边相等和平行四边形．由△AOE≌△COF，得EO=FO或AE=CF，继而通过对角线互相平分或一组对边平行且相等证得四边形AFCE是平行四边形.又因为EF垂直平分AC，所以AE=CE，故四边形AFCE是菱形．

思路2对角线互相垂直和平行四边形．同思路1先证得四边形AFCE是平行四边形，再加上已知条件EF⊥AC，即可证得四边形AFCE是菱形．

思路34条边相等．由EF垂直平分AC，可知点A和点C关于EF所在的直线对称，易得EA=EC，FA=FC，再通过证明△ECF是等腰三角形，即可证得四边形AFCE的4条边均相等，则四边形AFCE是菱形．

如果本题到此，那么这道例题的价值也即将被忽视．整个初中阶段要求掌握的数学知识点基本不会有什么改变，但是每年都会有层出不穷的新题，这些新题就来源于改题、编题．充分地讲解，适当地改变，再让学生积极思考，自主解答，前后联系，归纳思想方法，学生对知识点的理解一定可以更加深入，举一反三和独立学习的能力也会进一步提高．就此题而言，笔者有这样的几点思考：1)题目的条件是矩形ABCD，换成平行四边形可以吗？2)是否可以在原题的基础上增加问题的设置？3)菱形既是轴对称图形也是中心对称图形，是否可以将折叠问题与本题相结合？

2 对例题思考的探究

针对以上思考，在课堂上笔者组织学生展开了对此题的探究，以下是探究实录．

2.1 关注题目的背景条件，试图更改

思考1题目的条件为什么是矩形ABCD，换成一般的平行四边形可以吗？

通过提问引导学生在对问题解答后进行“由一般到特殊”的思考．在证明四边形AFCE是菱形的过程中，无论是哪种证法，矩形ABCD只发挥了一组对边平行的作用，而对于满足一组对边平行的四边形有很多，是否可以更改题目的条件，减弱题目的条件信息，可以怎样改？请小组讨论，给出改编的题目．

生1：可以把矩形ABCD改成ABCD．

生2：还可以改成梯形ABCD．

生3：其实只要满足AD∥BC的四边形都可以．

师：大家赞同以上同学的结论吗？咱们来画画图吧．

生4(补充)：在画图的过程中发现对角线AC的垂直平分线与边AD或BC有可能没有交点．

师(追问)：那么题目的描述应该怎样改变？

生5：可以把“与边AD，BC分别交于点E，F”改成“与边AD，BC所在直线分别交于点E，F”．

师：如果本题对于四边形的形状不做要求，那么题目可改为：“在四边形ABCD中，对角线的垂直平分线与边AD，BC所在的直线分别交于点E，F，问：四边形AFCE具有怎样的性质？”

生6：四边形AFCE是一个轴对称图形，也就是“筝形”．

师生共同总结归纳：

1)通过探究可以发现：筝形+一组对边平行→菱形．

我们知道平行四边形+一组邻边相等→菱形．其实这两种思路恰好体现了菱形的轴对称性和中心对称性．

2)再次温馨提示：在日后的解题中，审题一定要仔细，认真思考每一个题目的背景条件，想想这个条件能给解题带来什么有效的信息．除了本题之外，我们经常会在一些数学题中看到与某“直线”或“射线”或“线段”相交，这些微小的改变有时会完全改变一道题的结果．通常在看到“直线”或“射线”后，我们要进行全面思考，把可能出现的情况分析到位．

2.2 关注例题的问题设置，试图增设

思考2是否可以增加问题的设置？

一道题的价值不是通过一个提问就可以发挥全面，而应对这一道题进行深入思考.在本题中除了可以证明四边形AFCE是菱形之外，还可以发现当矩形ABCD的长与宽确定之后，菱形的底和高也是唯一确定的，那么菱形的底与矩形的长有什么关系等问题就产生了．在平时的问题教学中，我们要善于主动实施变式训练，通过多问、多思激发学生思维的积极性和深刻性．比如赋予矩形ABCD的长与宽，求菱形的边长、面积、对角线的长度等，题目可以改编如下：

变式1如图2，在矩形ABCD中，AD=9，AB=3，对角线AC的垂直平分线与边AD，BC分别交于点E，F.

图2

1)求证：四边形AFCE是菱形；

2)求AE的长；

3)求EF的长．

第1)小题就是例1．第2)小题求AE的长用到了方程思想：设AE=x，则DE=9-x．因为EF垂直平分AC，可得AE=EC．在Rt△DEC中，由勾股定理32+(9-x)2=x2，可解得x=5，即AE=5．

第3)小题中EF是菱形AFCE的一条对角线.要求线段长，可构造直角三角形，利用勾股定理求解，该思路比较容易想到.有学生给出了如下解法1和解法2．我们知道菱形的对角线互相垂直，而对角线的乘积的一半就是菱形的面积，因此要求其中一条对角线的长，可以用等面积法(如解法3)．

3)解法1(构造Rt△EFG)如图3，作EG⊥BC交BC于点G，由第1)和第2)小题得AE=5，四边形AFCE是菱形，可知AF=FC=5，从而GC=ED=4,于是FG=1.在Rt△EFG中，

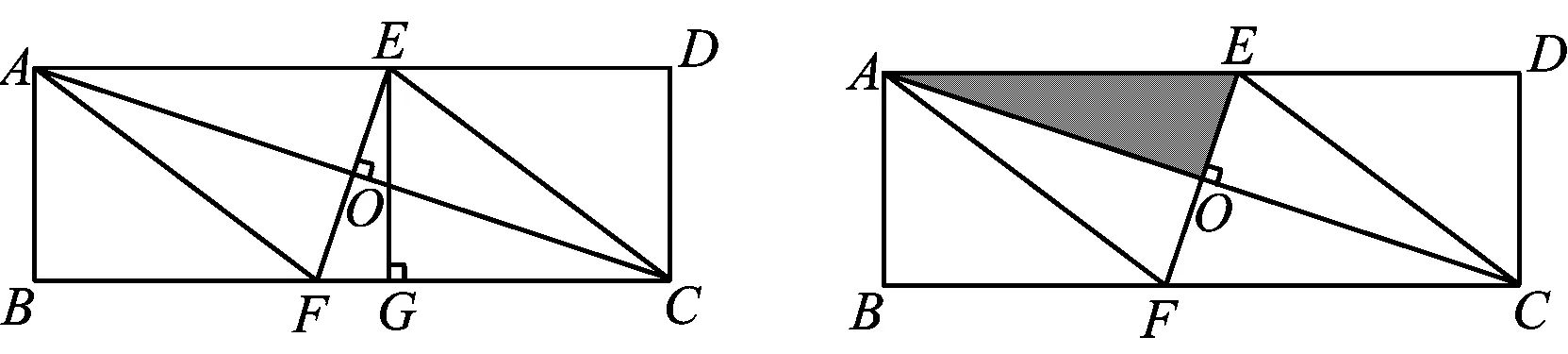
图3 图4

EF2=EG2+FG2=32+12=10，

故

解法2(找Rt△AEO)如图4,由第1)和第2)小题得AE=5，四边形AFCE是菱形.在Rt△ABC中，

AC2=AB2+BC2=32+92=90，

故

又因为四边形AFCE是菱形，所以

AO=OC,OE=OF,

从而

在Rt△AEO中，由勾股定理可得

解得

故

解法3(等面积法)如图4,由第1)和第2)小题得AE=5，四边形AFCE是菱形.在Rt△ABC中，

AC2=AB2+BC2=32+92=90，

故

于是

即

解得

2.3 关注例题的本质，试图建模

思考3菱形既是轴对称图形也是中心对称图形，如此对称的图形是否可以结合折叠问题？

笔者利用建模的思想将例题和配图做了完善，使其成为一个矩形的折叠问题．

变式2如图5，在矩形ABCD中，AD=9，AB=3，四边形ABFE沿着EF翻折，使点A恰好落在点C上.判断四边形AFCE的形状，并求出折痕EF的长度．

图5

折叠问题的本质就是轴对称性．而对于折叠问题，笔者曾做过一点探究，可以根据折叠后的位置进行分类.针对变式2，笔者继续思考：如果改变点A在翻折后的对应点A′的位置，使得四边形AFCE不是菱形，那么折痕EF的长度还可以求解吗？因此有了如下变式3：

变式3如图6，在矩形ABCD中，AD=9，AB=6，四边形ABFE沿着EF翻折，使点A恰好落在边CD的中点处，记为点A′，求折痕EF的长度．

图6 图7

这样的变式难度大了许多.笔者引导学生用例1求线段EF长度的方法来求解．学生给出了多种解法，其中还有一种不同于例1的解法，笔者既意外又惊喜．

解法1(方程思想，勾股定理)如图7，作EH⊥BC交BC于点H，联结A′F，设DE=x，则

AE=9-x.

32+x2=(9-x)2,

解得x=4，即DE=4,A′E=AE=5.

设BF=y，则FC=9-y,由翻折可得B′F=BF=y,A′B′=AB=6,∠B′=∠B=90°.在Rt△A′CF和Rt△A′B′F中,

32+(9-y)2=62+y2,

解得y=3，即BF=3,故

FH=BH-BF=AE-BF=2.

在Rt△EHF中，

EF2=FH2+EH2=22+62=40,

故

评注勾股定理在折叠问题中的应用具有典型性和普适性．不仅如此，在求解线段长度时也经常用到．解题时常常假设要求的线段或与该线段有关的线段的长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．

图8

评注这个解法可以说是一种“分离图形法”，从一个复杂的图形中抽离出基本图形，也可以是从一个复杂的问题中分离出一个个简单的问题．这样的解法不仅提升了学生的识图能力，而且可以让学生学会解“难题”——将难题分解成一个个简单的问题，逐一攻破．

解法3(借助等腰三角形、直角三角形)如图9，延长EA′,FC交于点T，作EH⊥BC交BC于点H，同解法1求出DE=4,EA′=5,易证△ETF是等腰三角形，从而△EDA′≌△TCA′，可得

图9

ET=2EA′=10=FT.

因为ED=HC=CT=4,所以

FH=10-8=2,

评注折叠带来了角平分线EF，与矩形中的两条对应边形成等腰三角形．利用等腰三角形的性质与勾股定理求出线段的长度．通过解法3可以发现学生的学习迁移能力是很强的.继续改变位置，比如改成三等分点或者4∶5的位置的点等，在学生学习了相似三角形之后，都可以手到擒来了．

叶圣陶先生说过：“教材只能作为教课的依据，要教得好，使学生受益，还要靠教师善于应用．”这就告诫我们要善于“用教材”，而不是“教教材”．只有理解教材，切合学生，对例题一题多解，解后思考；引申问题，丰富内涵；归纳题型，总结规律，才能有效地训练学生的思维能力，优化例题教学的效果[2].

3 如何优化例题教学

针对数学课堂，例题教学是非常重要的一个环节，是学习新知识的基础，需要教师对具体题目所涉及的知识与技能、数学思想方法有清晰的认识．教师通过对例题的开发、变式、建模，让学生在解决一个基本问题之后能够具备问题意识，学会解决一类题甚至几类题．《义务教育数学课程标准(2011年版)》(以下简称《课标》)中“四基”目标的达成，很大程度上依靠例题的教学来实现．而无论是数学思想方法的提炼还是数学基本活动经验的积累都需要依靠关键的例题．因此，如何优化例题的教学需要每一位教师认真思考，笔者认为可以从以下3个方面入手：

3.1 引导学生审视、更换题目的条件

我们经常会对学生说审题要仔细，作为学生学习的引导者，我们更应该发挥模范榜样的作用．在分析讲解一道题目的时候，对于题目表述的用词要多停顿、多琢磨；在对题目的理解欠佳时，可以通过更换题目的背景条件产生数学问题，帮助学生培养独立思考、举一反三的能力．比如文章中提到的“直线”“射线”“线段”的用词不同，用四边形ABCD来描述还是用以A,B,C,D这4个点为顶点的四边形来描述，用词不同可能造成题目的不同解．通过这样的审题、编题，可以帮助学生不因为看错题轻易丢分，通过用词更换产生的问题可以让学生对知识点以及数学思想方法理解得更加深入．

3.2 对例题进行二次开发

例题的运用如果是一次性的，那么这将会使得例题的作用得不到更有效的发挥．一道题开发得好，不仅可以减轻学生盲目刷题的负担，还可以帮助学生更加深入地理解题目．

3．3 基于例题和习题的建模

这里的建模指的是教师利用建模的思想，根据典型例题延伸出一类具有共性的题型．这样可以帮助学生更好地理解例题，学会归纳的思想，解决和掌握这一类题的通法，摆脱题海战术的枯燥．

《课标》强调：数学知识的教学，要注重知识的“生长点”与“延展点”，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性，体会对于某些数学知识可以从不同角度加以分析、从不同层级进行理解的过程．也就是说，在课堂教学中，要能够以课本例题为载体，进行一题多解或变式“改装”．数学的思想方法都隐藏在课本例题或习题中，我们在教学的过程中要善于对这类题进行深度挖掘，这不但能够培养学生的探究能力、归纳能力，而且有利于学生知识体系的建构．

综上所述，在对数学教材中的例题进行教学时，要认识到学生不是通过做一道习题就能对该知识点有充分的掌握．为了使学生能够更好地掌握数学知识，领悟到思想方法，我们应对例题进行认真思考，挖掘出例题的价值，真正做好例题的教学．