关注生之问 探寻教之策——以一道数列通项题的求法为例

郭建华, 于 健, 张云飞

(1．金陵中学，江苏 南京 210005；2．南京市鼓楼区教师发展中心，江苏 南京 210017)

对于数学解题教学，章建跃先生曾指出：要以如何发现和提出问题、如何获得数学对象、如何构建研究线索以及掌握解决问题的基本方法等为目标，即要让学生通过解题逐步学会认识和解决问题的基本方法．数学教学是以解题为中心展开的．然而，在当下课堂教学中，有的教师为了赶教学进度，把试题讲完就算完成任务了．在这种高容量、快节奏的课堂模式下，学生有思考的时间吗?有交流的机会吗?有探究的空间吗?在这样的境况下，何谈落实“四基”，培养“四能”，发展学生的数学核心素养？只有在解题教学中多和学生交流、沟通，才能了解学生需求什么(还学生话语权)、存在哪些困难(优化解题路径)，并通过设计精准、有效的解题教学方法和策略，让学生“知其然，知其所以然，何由以知其所以然”，真正促进学生学会解题．下面，笔者以一堂复习课上的解题教学为例，谈谈自己的做法和思考，供参考．

1 题目再现

例1已知各项都为正数的数列{an}满足an+2=2an+1+3an．

1)证明：数列{an+an+1}为等比数列；

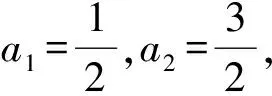
(2021年“八省(市)”联考数学试题第17题)

本题考查了依据连续3项的数列递推关系，求数列通项公式、证明等比数列等；考查学生灵活运用“转化与化归”思想进行解题的能力．

2 关注生之问

考后学生没有终止对这道题的探究，感兴趣的学生对这道题提出了一些问题，笔者梳理如下：

1)命题人是如何想到数列{an+an+1}为等比数列的?

2)如果改变an+2=2an+1+3an中项的系数，那么{an+an+1}是否仍为等比数列?

3)如果没有第1)小题，那么{an}的通项公式如何求?

4)求这类数列的通项公式是否存在统一的方法?

5)是否存在一个更一般的结论?

教师应该及时分析学生所提出的问题，因为它们是学生真实学情的反映，是学生现有认知水平的体现，是学生某些知识和方法缺失的暴露等．教师要与不同层次和需求的学生多沟通和交流，在遵循学生思维特点的基础上，开发好学生所提出的问题资源．面向全体学生以“最近发展区”理论设计探究教学，探寻适合学生的教学策略，让更多的学生真正做到思维的参与，从而达到教师教得“精准”、学生学得“深刻”的效果．

3 探寻教之策

3.1 引入辅助题目，以退求进

在波利亚的“怎样解题表”中提到：如果你不能解所提的题目，就先尝试去解某道有关的题目．你能否想到一道更容易着手的相关题目?一道类似的题目?……为了更好地解决学生的问题，选好探究问题的起点至关重要．

下面，先从学生熟悉的、连续两项的递推关系着手．

例2已知各项都为正数的数列{an}满足an+1=2an+3且a1=2，求{an}的通项公式．

由于学生对该题型比较熟悉，很快得到如下解法：

解法1(配凑法)将an+1=2an+3恒等变形为

an+1+3=2(an+3)，

因为a1+3=5≠0，所以{an+3}是公比为2、首项为5的等比数列，易求其通项公式为an=5×2n-1-3．

解法2(迭代法)由a1=2，an+1=2an+3，得

a2=2a1+3，

a3=2a2+3=22×a1+2×3+3，

a4=2a3+3=23×a1+22×3+2×3+3，

…

以此类推，得

an=2an-1+3=2n-1×a1+2n-2×3+…+2×3+3

=5×2n-1-3．

解法3(叠加法)由an+1=2an+3，a1=2，得

即

利用叠加法，易得an=5×2n-1-3．

有学生提出：解法1是如何想到的?如果所给的系数不是很好凑，那么又如何求解呢?让学生讨论并发现“巧妙配凑”背后隐藏的东西．让学生体会“配凑”的目的，就是将非等差、非等比数列转化为等差、等比数列．为了达到“式子结构”上的一种“平衡”，自然就会想到从系数入手，从而引入待定系数法，揭开了“巧法”的神秘面纱，解除了学生心中的疑惑．

解法4(待定系数法)设an+1+t=2(an+t)，其中t为待定的非零常数，即an+1=2an+t，与an+1=2an+3比较系数，得t=3，即an+1+3=2(an+3)，下面求解同解法1(略)．

趁机，让学生抽象出更一般的结论：若an+1=qan+p(其中pq≠0且q≠1)，则令an+1+λ=q(an+λ)，a1+λ≠0，再利用等比数列求其通项.

评注解法1技巧性较强，具有“想的巧，算的少”的特点；解法2通过特殊项探究一般项的规律，体现了从特殊到一般的解题思想；解法3通过分析式子的结构特征，将其恒等变形为可利用叠加法求通项的形式，体现了“转化与化归”的数学思想；解法4其实就是利用方程的思想换一种方式表征常数项．通过各种解法的比较，让学生体会到待定系数法的操作性更强．

3.2 巩固通项求法，变式跟进

在例2的基础上，教师给出相似题组变式，让学生思考能否从以下问题的解决，提炼出求解这类问题的更一般的思路和方法．

变式1已知数列{an}满足an+1=3an-4n，a1=3，求{an}的通项公式．

变式2已知数列{an}满足an+1=3an-n2，a1=3，求{an}的通项公式．

变式3已知数列{an}满足an+1=3an-4n，a1=3，求{an}的通项公式．

给学生时间，4人一组，让他们完成以上各变式的解答．分析和比较每道题的解法，在教师的引导下让学生提炼出待定系数法，体会它在每个问题中的不同呈现方式．

继续组织学生分组讨论，抽象出以上各题所具有的一般的结构：an+1=qan+f(n)(其中q≠0且q≠1)，并对待定系数的表征形式进行归纳和梳理．

1)若f(n)=an+b(其中a为非零常数)，则令an+1+λ(n+1)+μ=q(an+λn+μ)；

2)若f(n)=an2+bn+c(其中a，b为非零常数)，则令an+1+λ(n+1)2+μ(n+1)+c=q(an+λn2+μn+c)；

3)若f(n)=an(其中a为非零常数)，则令an+1+λ×an+1=q(an+λan)．

评注变式教学是一种行之有效的教学方法，课堂上要充分发挥学生的主观能动性，在教师引导下激发学生的探究热情，培养学生发现和提出问题的能力，提高分析和解决问题的灵活性，巩固和理解所学的知识和方法，揭示问题的本质，增强学生的认知水平和主动探究问题的意识．

3.3 依托变式探究，深化理解

通过对例2以及变式的分析，引导学生继续思考：如果出现连续3项的递推关系呢？那么待定系数法是否依然适用?给予充足的时间让学生尝试操作．

有学生立刻想到令f(n)=3an，下面，请学生用待定系数法分析求解例1．

由an+2=2an+1+3an，令an+2-λan+1=μ(an+1-λan)，得

an+2=(λ+μ)an+1-λμan，

与an+2=2an+1+3an比较系数，得

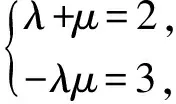
解得

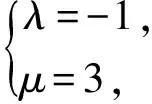
故

an+2+an+1=3(an+1+an),

或

an+2-3an+1=-(an+1-3an).

至此，不仅发现了命题人如何命制{an+an+1}为等比数列的“小秘密”，而且还找到了求解这类问题的通性通法．同时，学生还获得了一个意外的收获，那就是又构造出了一个数列{an+1-3an}.

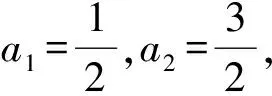
a2-3a1=0，

当n≥2时，

an-3an-1=0，

即

an=3an-1，

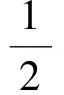
学生感觉收获颇大，探究的热情被激发起来了，抓住这个契机，放手让他们继续探究．伴随着问题的解决，有学生发现，构造数列{an+an+1}或{an+1-3an}，求{an}的通项是相同的，这是为什么？它们之间存在怎样的联系？

又产生了一个新的问题，大家的思绪又聚集起来了．等待片刻，一位学生提出，其实反映的就是一个问题的两种不同的表现形式，即

an+2=2an+1+3an，

an+2+an+1=3(an+1+an)，

an+2-3an+1=-(an+1-3an),

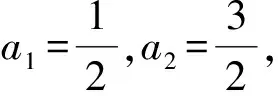
下面继续参照例1，让学生来做一回“命题专家”，能否利用已经掌握的知识和方法编拟类似于例1的试题.大家开始投入编拟试题的状态，教师巡视，选用几道典型的问题作为大家的课堂巩固练习．

变式4求满足下列条件的数列{an}的通项公式：

1)a1=1，a2=2，an+2=2an+1-an；

2)a1=1，a2=2，an+2=an+1+an；

3)a1=1，a2=2，an+2=2an+1-2an．

通过变式4的练习，学生在解题的过程中又发现了新的问题，有的二阶线性递推数列的特征方程有实数解，有的无实数解，教师给予说明，对于无实数解的暂不研究．对学生编拟的试题教师要给予指导和积极的评价，只要理解问题的背景，抓住命题的核心要素，编拟试题将不是难事．通过“命题”活动，让学生体验学习的乐趣，增强学习数学的信心．

评注只要给学生时间和空间，一定会呈现惊喜.学生通过探究，在思考和交流中抽象和归纳出求解问题的一般方法.在教师的引导、鼓励、帮助下，学生在“做数学”的同时体验成功的快乐和感悟探究的乐趣.

3.4 探究一般形式，融会贯通

通过以上分析，教师规定只要研究待定系数为实数的情况，继续让学生探究更一般化的结论．

例3[1]设数列{an}满足：a1=a，a2=b，an+2=pan+1+qan(其中pq≠0)，求an．

分析令an+2-λan+1=μ(an+1-λan)，则

an+2=(μ+λ)an+1-λμan，

从而

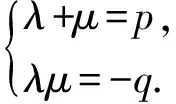
易知λ,μ为方程x2-px-q=0的两个根，当Δ=p2-4q≥0时，设该方程的两个根分别是α,β，则

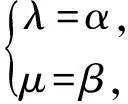
故an+2-αan+1=β(an+1-αan),

或an+2-βan+1=α(an+1-βan).

当a2-αa1≠0，a2-βa1≠0时，数列{an+1-αan}，{an+1-βan}分别是公比为β，α的等比数列，从而

an+1-αan=(a2-αa1)βn-1,

(1)

an+1-βan=(a2-βa1)αn-1.

(2)

根据前面解题方法的提炼，学生很容易得到式(1)和式(2)，面对这两个式子，如何确定数列的通项呢?经过讨论，得到以下两种情况：

1)当α≠β时，式(1)两边同时除以αn+1，或式(2)两边同时除以βn+1，再利用叠加法求得

获得结果的过程还是比较艰辛的．教师让学生观察和讨论有没有更简捷的办法得到an，有的学生想到前面已经分析过式(1)和式(2)都是数列{an}的两种不同表征形式，因此，由式(1)-式(2)，得

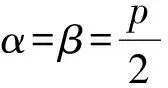
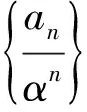
有的学生对“二阶线性递推数列的特征方程”不熟悉．下面，教师给予补充说明：

1)方程x2=px+q叫做二阶线性递推数列的特征方程，λ,μ是其特征根．其特征方程可以由所给的二阶递推数列直接得到．

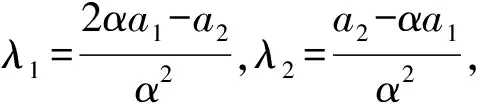
an=(λ1+λ2n)αn；

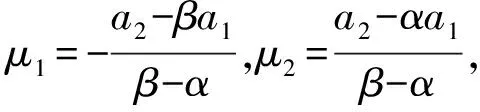
an=μ1αn-1+μ2βn-1．

再结合已知条件，便可迅速确定待定系数，让学生再次感受待定系数法在处理问题中的重要作用．

学生再次发现，有了这种简约的表达形式后，对于研究an+2=pan+1+qan的通项更为方便．继续让学生练习变式4中的第1)和第2)小题，让学生体验这种简捷形式的表达．其解题过程(略).

评注让学生体会从特殊化到一般化，再从一般化再到特殊化的探究问题的思维路径，旨在引导学生学会思考和学会解题，将所学的知识融会贯通，让学生的理解进一步得到深化和升华，达到举一反三、触类旁通的效果．

4 教学反思

4.1 鼓励学生发现问题和提出问题

善于从学习材料中发现问题，并通过抽象、概括提出问题的能力是当前学生的“短板”，应予以重视．对于学生能发现和提出的问题，教师要给予积极的评价和鼓励，以便更好地保护学生提出问题的积极性．只有关注学生发现问题和提出问题能力的培养，才能真正落实以学生发展为本、立德树人的根本任务，培育科学精神和创新意识，提升数学核心素养[2]．从数学的角度发现和提出问题应该渗透在日常的探究教学中，教师给予正确、适时的引导和帮助，为学生提供机会，鼓励学生敢于质疑、善于思考．通过学生发现和提出的问题，判断学生对知识的理解和对方法的掌握程度，进而更精准和更有效地调整“教”与“学”的行为．

4.2 注重学生自主探究和合作交流

解题教学活动的重心应该放在促进学生学会解题上，积极探讨有利于促进学生解题的教学方式、方法和策略，在教师引导下进行“再发现和再创造”的解题探究活动．在学生已有认知的基础上展开，选择适宜学生探究的起点，不仅能对问题的求解起到启迪作用，而且还能激发学生探究的热情．本节课采取“以退求进”的策略展开教学，在教师引导下，让学生在“做中学”和“学中做”，让学生表达和交流，发现“巧法”背后的“秘密”，进而找到解决这一类问题的一般方法．为了更好地促进学生对数学思想和方法的理解，让学生通过小组合作“编拟”试题，从而对试题不断进行修正和优化，进一步探究、归纳、提炼出更一般的结论，培养学生的团队协作意识和科学精神．教师通过从特殊到一般，再从一般到特殊的解题方式教学，让学生体验和掌握一种探究问题的方式，真正达到“授人以渔”的效果．