风电偏航轴承接触力分布与疲劳寿命分析*

黄龙艺 刘宇祺 王 华 刘 赛

(1.南京工业大学机械与动力工程学院 江苏南京 211816;2.南京工程学院机械工程学院 江苏南京 211167)

偏航轴承是一种大型、重载的特殊轴承，是风力发电机组中的核心部件，通常由带齿的内圈、外圈、钢球以及安装螺栓构成。其通常安装在风机机舱支撑结构上，根据风向调整风机迎风角度，起到了承载、导向和定位的作用。偏航轴承工作环境恶劣，承受较高的载荷，一旦失效，将造成整机无法运行，甚至会引发意外事故。因此，研发承载能力强、疲劳寿命高的偏航轴承具有重要的工程应用价值。

目前，国内外对大型轴承的研究，除了研究其失效机制外，其他研究内容还包括轴承接触力分布、承载能力的研究以及疲劳寿命的预测。贺业成、王燕霜等[1-2]建立回转支承的力学模型，研究了不同间隙下回转支承的承载能力。HE等[3-4]基于有限元方法构建轴承的等效接触模型，分析了不同滚道硬化层下的应力分布，从而确定最优的滚道淬火深度。张杰毅等[5]采用损伤力学和有限元计算相结合的方法，对球轴承的疲劳寿命进行预测，并开展疲劳强化实验验证了分析的正确性。AGUIRREBEITIA等[6]通过假设滚道为刚性体，构建了单排四接触点转盘轴承的力学模型，获取了极限接触力作用下的载荷接收曲线。王存珠等[7]分析了安装螺栓的预紧力对双排球式转盘轴承接触力的影响，表明非均布的预紧力会引起轴承接触力分布的波动。姬丽丽、WANG等[8-9]建立了三排滚柱式转盘轴承的有限元模型，通过将滚子等效为非线性的弹簧单元，减低了计算的规模，并进行压痕实验验证了非线性弹簧模型。王自彬等[10]分析了径向载荷、间隙、转速等对轴承运行稳定性的影响，研究表明载荷和间隙对运行稳定性的影响不是恒定的。牛荣军等[11]采用有限元方法分析了滚轮滚针轴承的承载能力，探讨了载荷、游隙、偏斜角对承载能力的影响。GÖNCZ等[12]用向量法求解三排滚柱式转盘轴承的承载能力，通过将滚子简化成非线性单元，考虑了间隙、制造误差、偏斜角等参数的影响。但该文献分析中未考虑套圈的变形量，为了提高计算精度，HERAS等[13]提出了理论分析法和有限元法耦合的半分析模型，该模型中考虑了套圈的变形。ZUPAN和PREBIL[14]构建了轴承承载能力和承载角、滚道曲率半径系数的函数关系，研究表明滚道变形会改变实际的承载角。GÖNCZ等[15]基于滚子和滚道的等效接触模型，在考虑滚道弹塑性和淬火硬化层深度的情况下，分析了不同修型滚子的应力场分布情况。

综上所述，许多学者对偏航轴承的承载能力和疲劳寿命开展了研究，但有关的静载实验研究还很少，同时轴承结构参数对接触区域应力场和疲劳寿命的影响需要进一步研究。因此，本文作者首先提出一种关于偏航轴承的有限元等效建模方法，获取轴承的接触力分布，并开展静载实验验证计算的正确性；随后，将求得的最大接触力施加给钢球与滚道的等效模型，获取接触区域的应力场；最后分析轴承接触角和滚道半径系数等结构参数对接触应力场合疲劳寿命的影响。

1 轴承有限元模型建立和实验验证

1.1 等效模型的建立

以010.40.1000单排四点接触偏航轴承为研究对象，其滚道截面见图1。滚道由4部分构成，各部分的曲率中心为Cid、Cod、Ciu、Cou(下标字母i、o分别对应内、外圈，u、d分别表示上、下滚道)。具体的结构和材料参数如表1和表2所示。其中轴承接触角α为45°，滚道半径系数f为1.05,轴承的滚道半径系数f可由以下公式来计算：

表1 偏航轴承结构参数

表2 偏航轴承材料参数

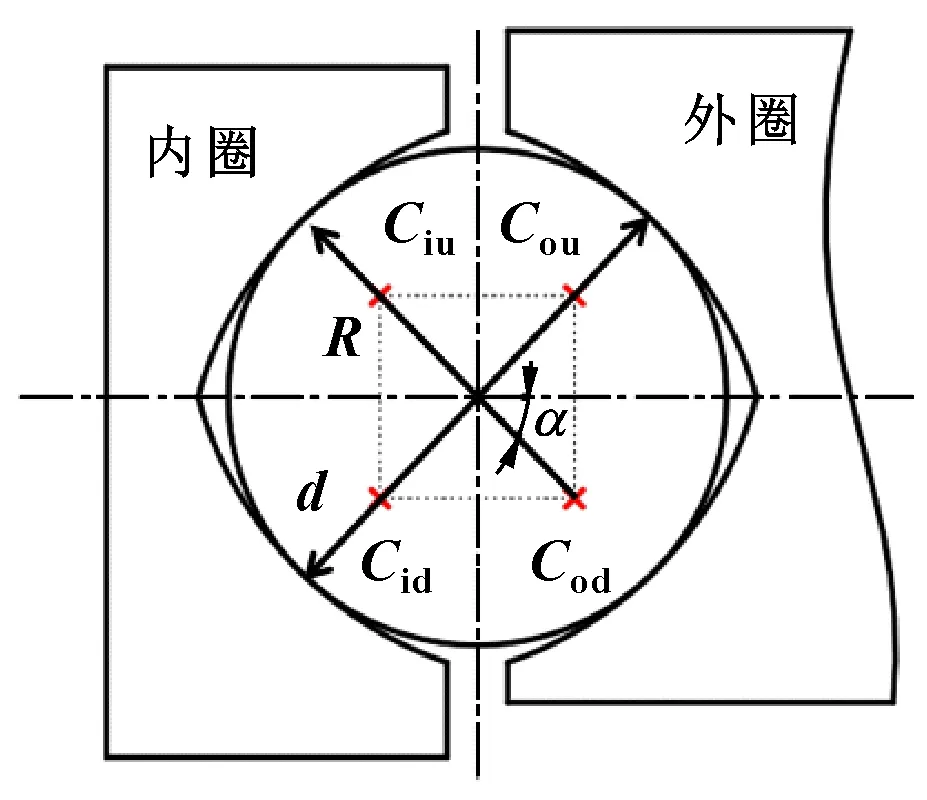
图1 滚道截面

(1)

式中：d为钢球直径；R为滚道曲率半径。

在钢球与滚道的赫兹接触中，钢球的接触力和变形关系[16]可表示为

(2)

式中：δ为钢球的变形量;Q为钢球的接触力。

偏航轴承通常承受倾覆力矩M、轴向负载Fa和径向负载Fr，根据经验公式，滚道上最大接触力Qmax[17]为

(3)

式中：n为钢球数量;D为滚道节圆直径。

公式(2)表明了钢球与滚道的非线性接触关系，因此，在建模中可采用非线性的弹簧单元模拟钢球-滚道的接触行为。钢球与滚道只在受压时产生变形，通过将图2中所示的接触力和变形量赋予弹簧单元，使弹簧单元与钢球的接触变形特征一致。模型中使用两根弹簧取代一个实体钢球，通过连接滚道中心的对角点，生成弹簧单元，并将滚道中心处的节点与滚道上的表面进行耦合约束。偏航轴承的等效模型如图3所示。根据赫兹接触理论，与滚道中心节点耦合的表面的尺寸为

图2 载荷变形曲线

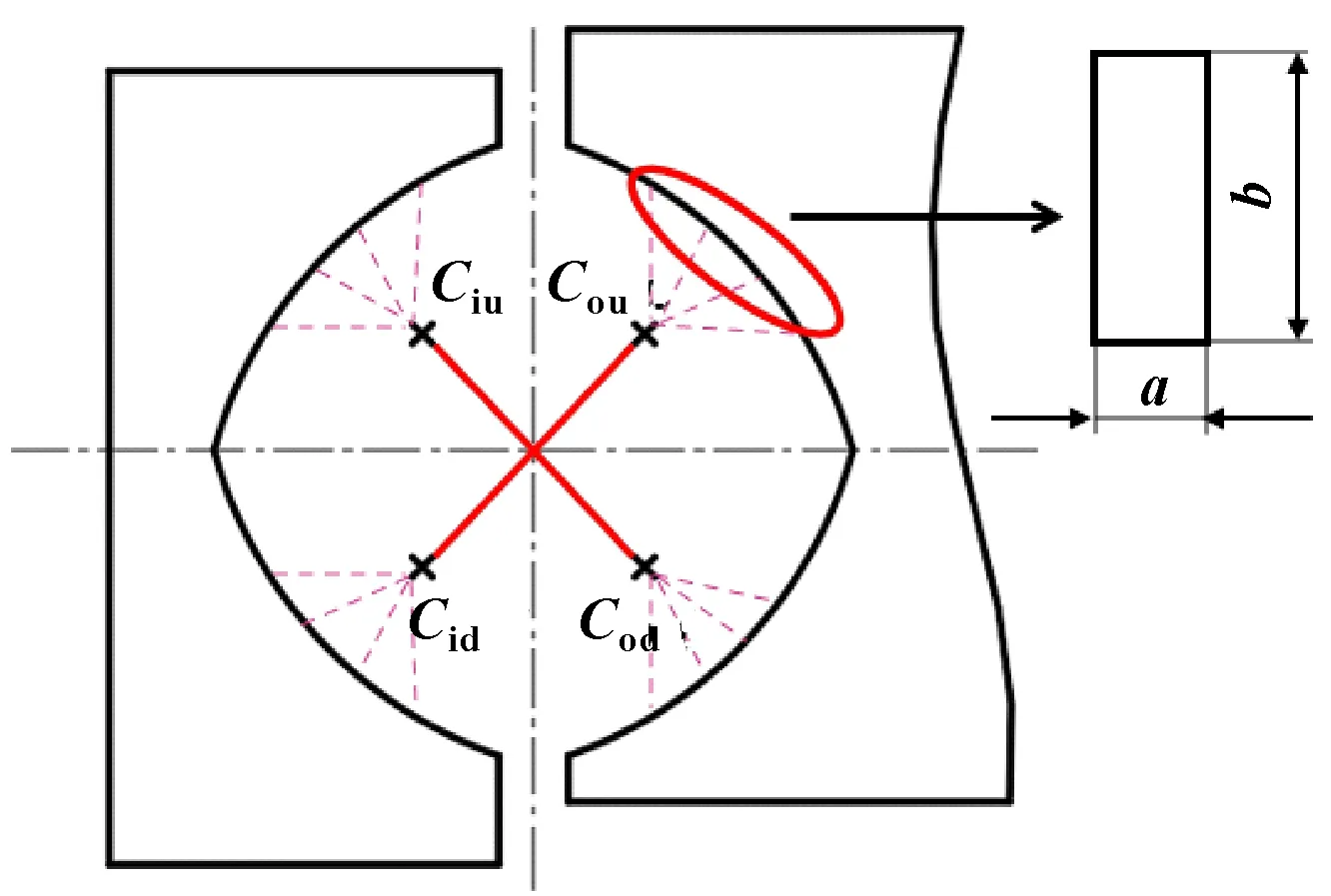
图3 等效模型示意

(4)

(5)

式中：a为耦合表面的宽;b为耦合表面的长。

建模时忽略结构中的小导角、油孔、内圈的轮齿等细节，以降低计算规模。轴承的整体模型如图4所示。为了便于观察各个钢球的接触力分布，对非线性弹簧对进行编号，见图5。在内圈和外圈的几何中心创建参考点RP-in和RP-out，将RP-in和RP-out分别与内、外圈安装结合面定义成耦合关系。在010.40.1000偏航轴承中，内圈固定，外圈可进行回转。因此，约束RP-in的所有自由度，释放RP-out轴向、径向的平移自由度和倾覆力矩的旋转自由度。施加的载荷值为轴向力Fa=520 kN，径向力Fr=175 kN,倾覆力矩M=450 kN·m。

图4 整体模型

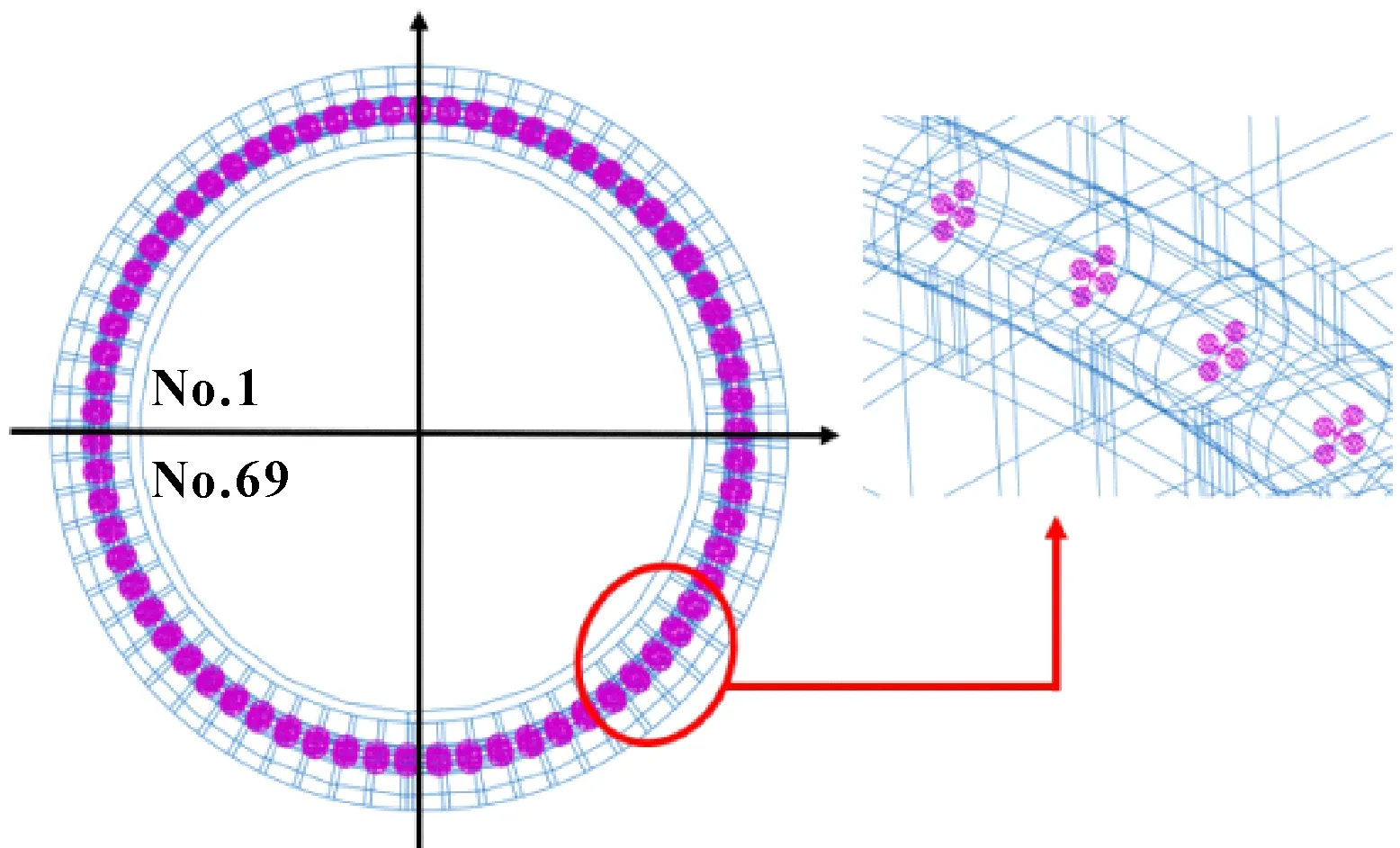
图5 非线性弹簧模型编号

提取弹簧中的载荷值，生成图6所示的接触力分布曲线。其中在No.68处的钢球有最大接触力，为47 776，而由经验公式(3)求得的最大接触力为54 826 N，误差为14.7%。仿真和理论结果的差异是由经验公式中的简化和假设引起的。理论方法认为轴承套圈是刚性的，而在有限元模型中，套圈在外载的作用下会变形。因此，有限元模型仿真得到的钢球的最大接触力与经验公式计算结果有所不同。从轴承的实际工作条件方面考虑，可将仿真分析的结果用于后续分析。

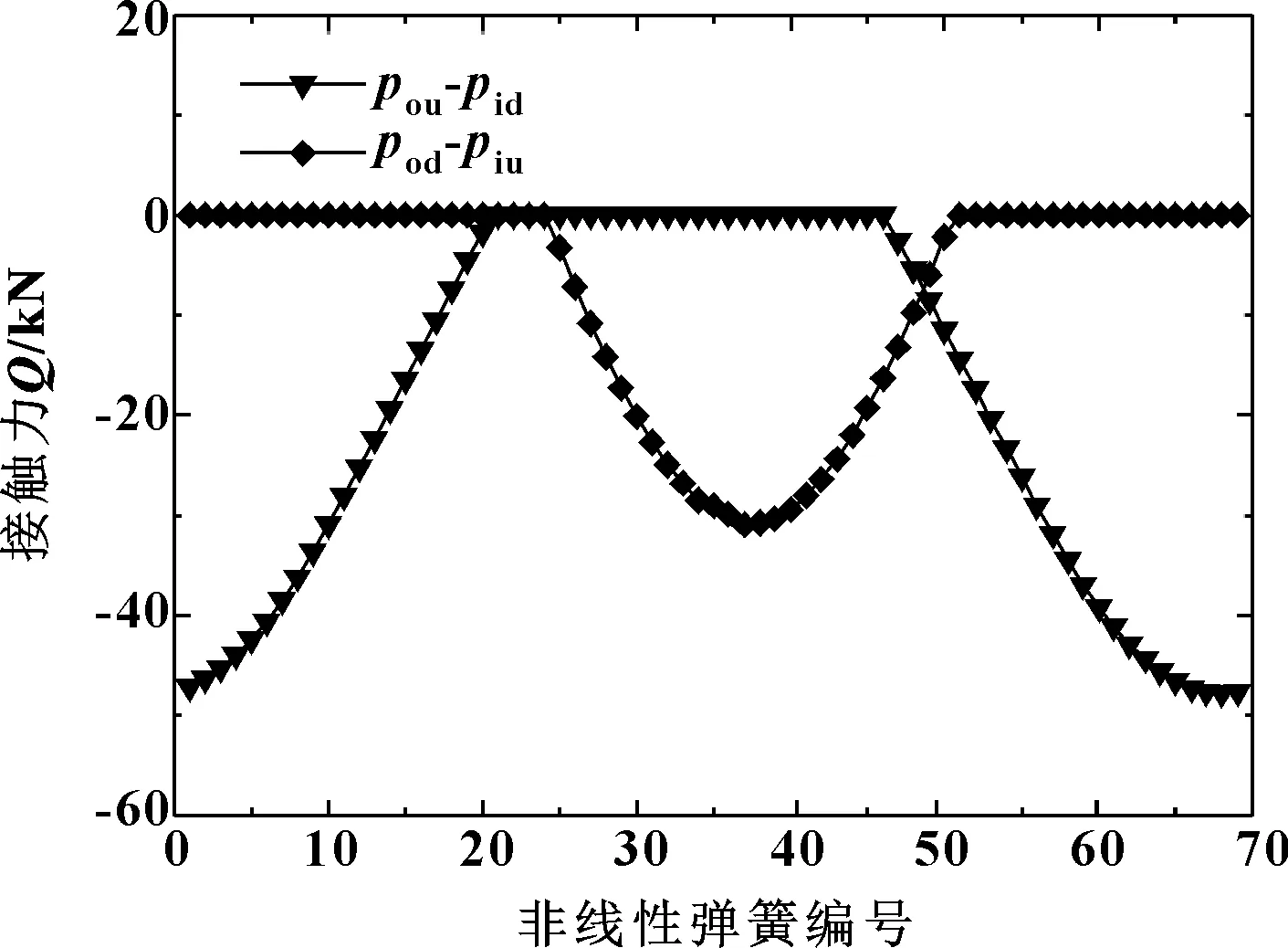
图6 接触力分布曲线

1.2 静态加载实验

为了进一步验证有限元模型的有效性，设计并开展了偏航轴承的静态承载实验。实验在小型偏航轴承实验台上进行，如图7所示。该实验台可同时对轴承施加倾覆力矩、轴向力和径向力。测试轴承以螺栓固定的形式固定在安装法兰上，其上端与加载盖连接，而加载盖与液压缸G1、G2、G3相连，通过液压缸的组合作用，实现不同的载荷输出。

图7 偏航轴承试验台

考虑到钢球与滚道的接触力无法直接获取，因此，实验中采用一种间接测量的方法，即通过在轴承内侧的圆周面均匀布置应变片，获取接近滚道外侧处的应力分布。如图8(a)所示，在轴承内侧布置69个箔式应变片，为了便于观察测量结果，对应变片进行编号，见图8(b)。测试中使用DH3815N-3应变系统，测量时进行温度补偿。为了保证数据可靠性，分别对轴承进行3次加载，每次加载的载荷如表3所示。

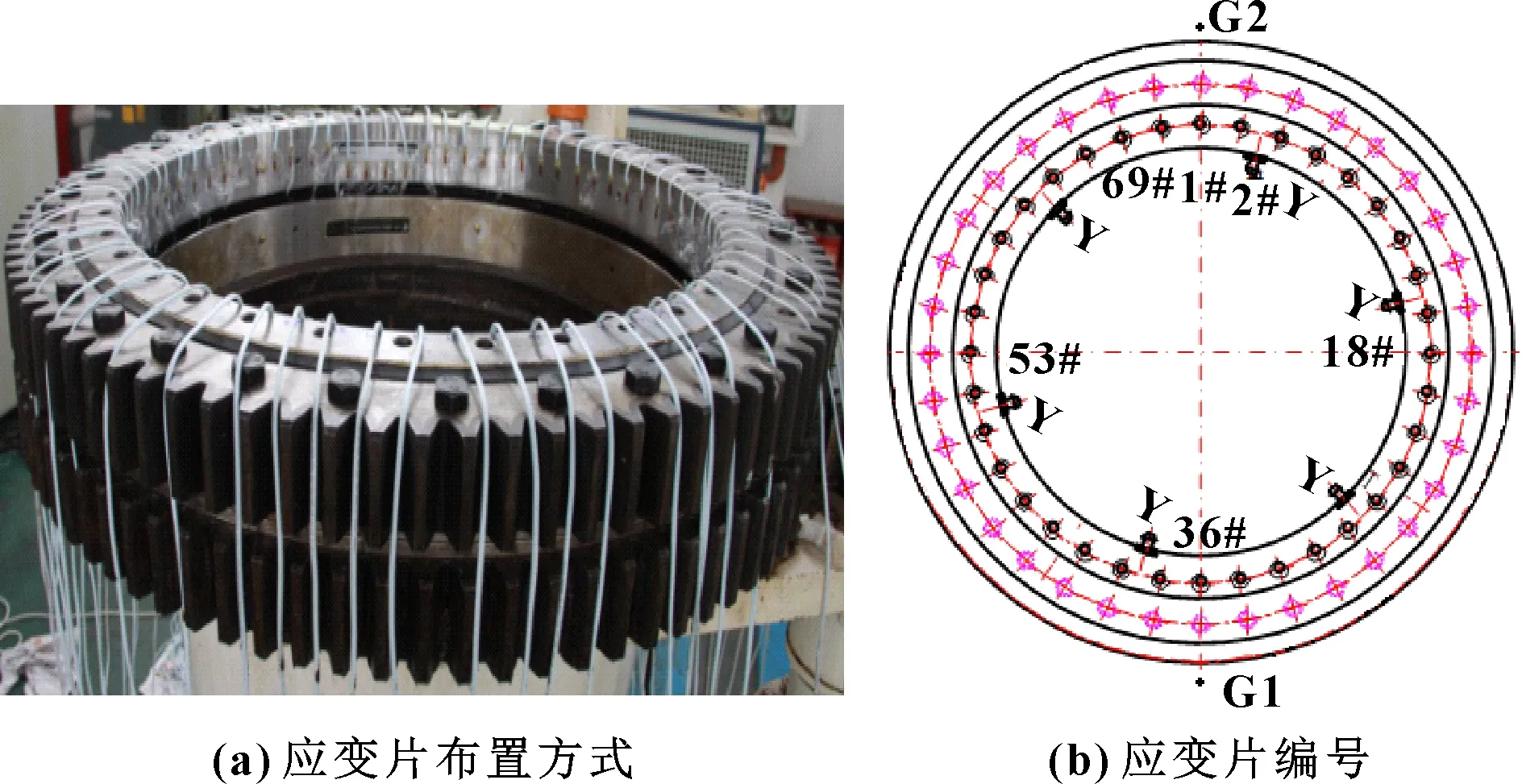
图8 应变片布置方式及编号

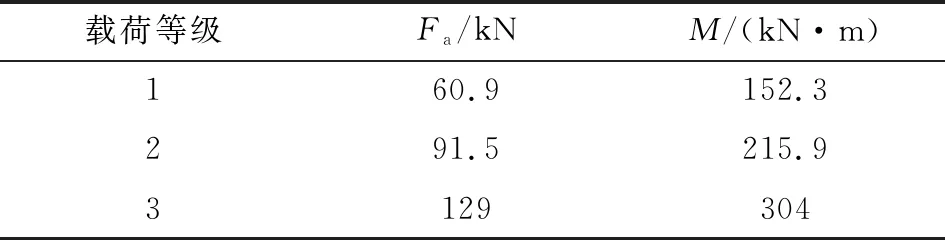
表3 施加的载荷值

实验开始前，令轴承以4 r/min的转速低速运转，待轴承运行平稳时，停止运转，此时轴承内部钢球与滚道已充分接触；随后，开始对轴承进行逐级加载。各级加载下测得的结果如图9所示，总体上，实验结果和仿真计算的变化趋势一致。但是，在编号No.15～25测点处，数值波动较大。造成实验结果和仿真误差的原因主要有：应变片安装表面处存在锈渍、沟壑等；轴承内圈处留有油孔的位置，使应变片无法均匀布置在安装表面上。综合分析在不同的载荷作用下结果，实验和仿真的应变最大值都出现于编号No.35的测点处，从一级加载到三级加载中，在编号No.35测点处的误差分别为8%、9.3%、8.4%。综合来看，实验结果和仿真分析结果的误差在可接受范围内，验证了非线性弹簧模型的有效性。

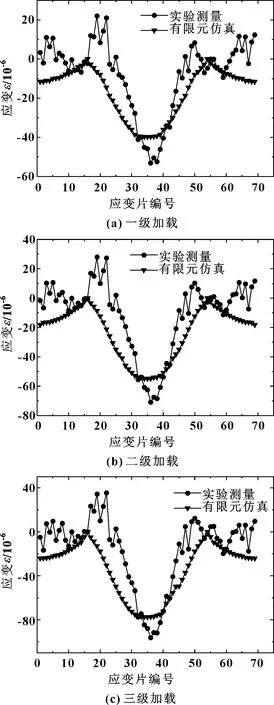
图9 实验与仿真结果

2 接触应力场和疲劳寿命分析

2.1 应力分析

当钢球和滚道表面承受压力时，接触点附近因为挤压而产生变形，最终形成椭圆形的接触面。根据赫兹接触理论[18]，接触面处的最大接触压力S为

(6)

式中：Q为接触力；a和b分别为接触面的长半轴和半轴，可由以下公式表示：

(7)

(8)

∑ρ=ρ11+ρ12+ρ21+ρ22

(9)

(10)

式中：∑ρ为钢球和滚道总的曲率比，接触体的曲率如图10所示；F(ρ)是主曲率函数，α和β依据F(ρ)来获得[18]。

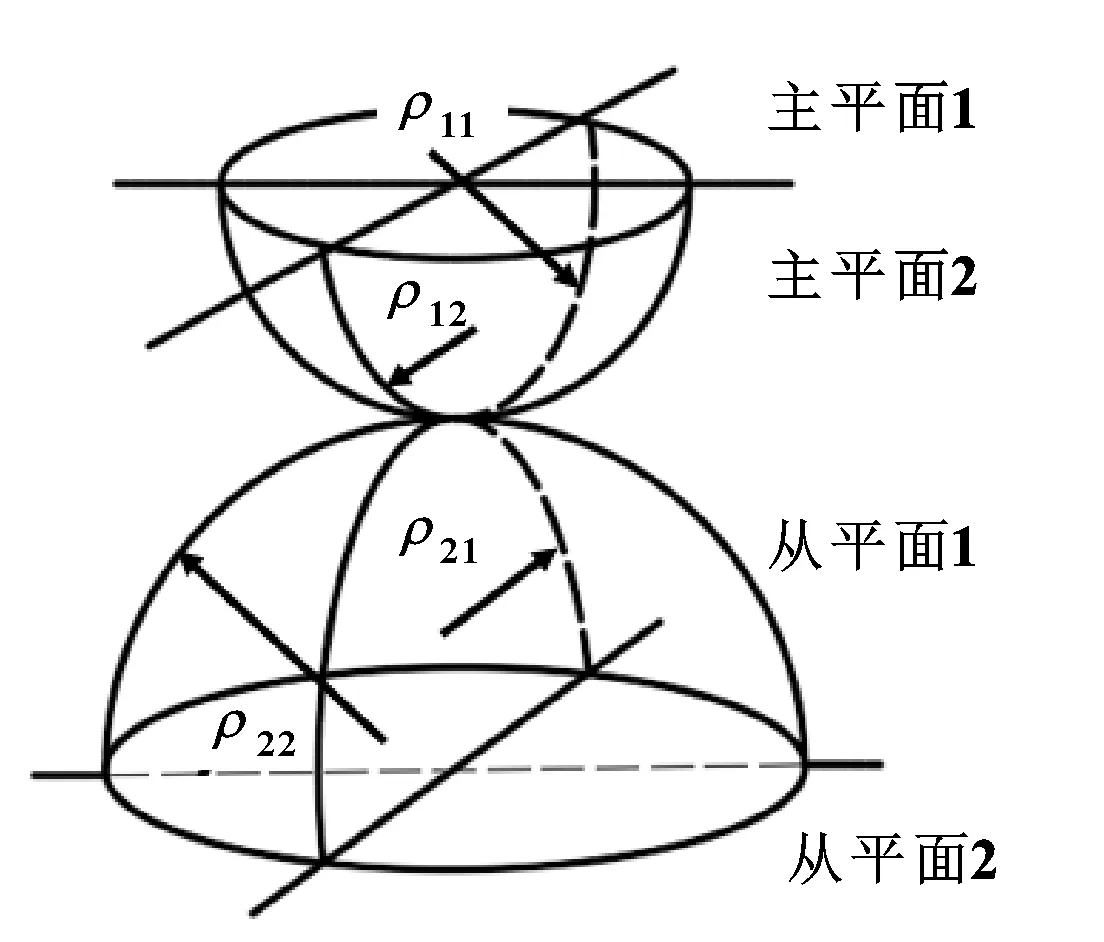
图10 曲率和主从面

进一步地，为考察钢球与滚道接触的应力分布情况，建立起钢球与滚道的等效接触模型。建模时，从减小计算规模和提高效率的方面考虑，根据偏航轴承的对称结构，选取了1/8的钢球和滚道接触模型进行计算，如图11所示。将对称面设置为对称约束，释放钢球Y轴方向下压的自由度。对于非线性接触计算，网格密度对分析结果有重要的影响。因此，对钢球和滚道的接触区的网格进行了加密处理，单元类型为C3D8R。由非线性弹簧模型求得钢球最大接触力为47 776 N，分析中只选用1/8的接触模型，所以施加的接触力Q为5 972 N。

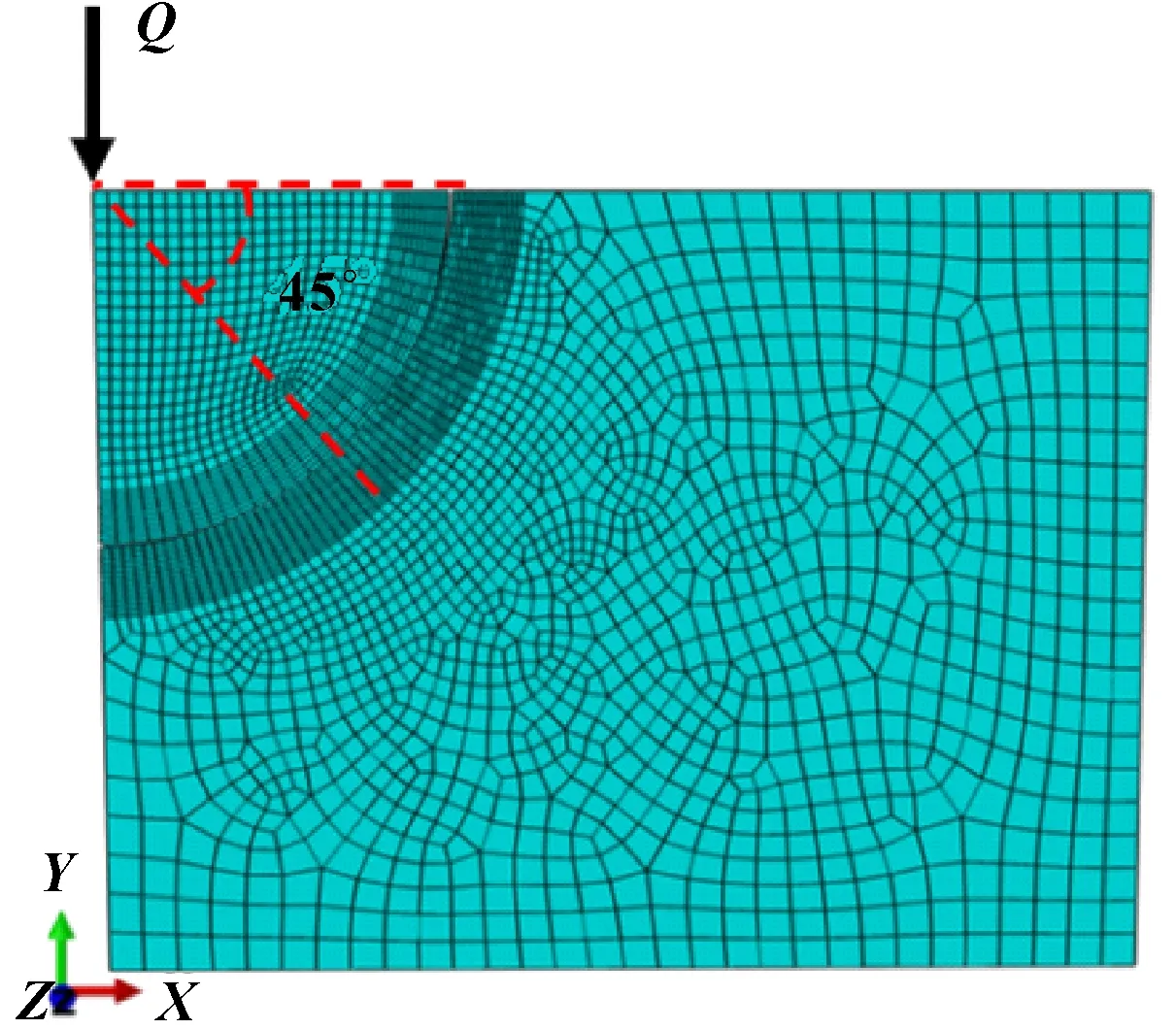
图11 等效接触模型

由图12可知，接触区域近似为椭圆形，在接触区域的中心应力值最高，为2 079 MPa。根据赫兹接触理论得到的接触应力为2 327 MPa，与仿真结果误差为10.6%，验证了有限元模型的正确性。但是赫兹接触理论简化了钢球与滚道的接触行为，而仿真分析可以考虑实际的工况如摩擦因数、接触角、滚道半径系数等。因此，在偏航轴承的应力场分析中，有限元方法比理论计算更可靠。

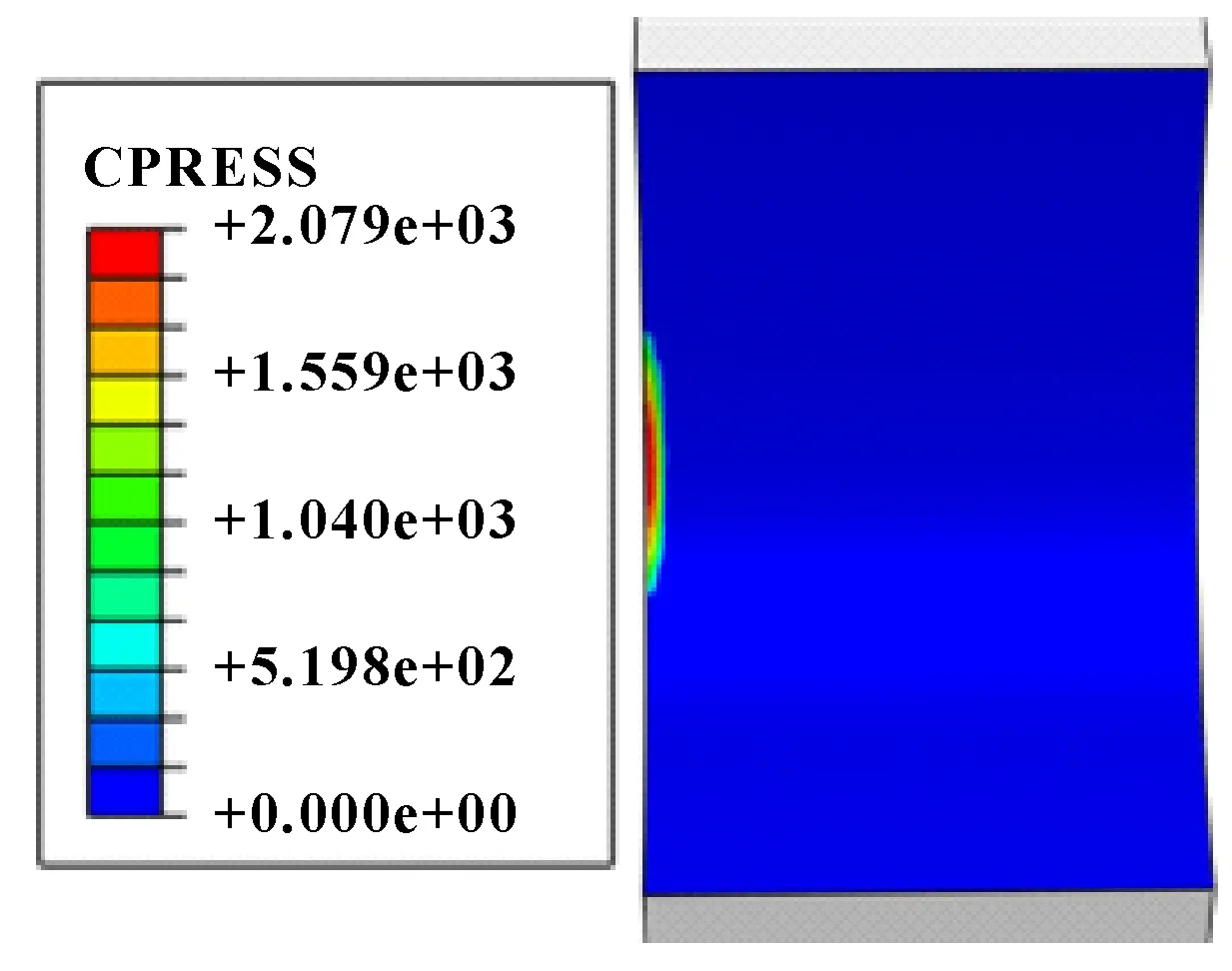
图12 接触应力云图(MPa)

von Mises屈服准则考虑了第四强度理论的独立法向应力和剪切应力的组合效应，认为当某处的等效应力达到一定值时，该点开始进入塑性状态。在分析中，010.40.1000偏航轴承滚道处的Mises应力场如图13所示，可知最大Mises应力为1 269 MPa。轴承滚道承受交变应力的作用，是最容易出现疲劳损伤的区域，图14表示了沿滚道表层深度的应力分布，其中，在表层深度0.5 mm处应力值最大，该位置往往出现剥落、压溃、塑性变形等失效形式。

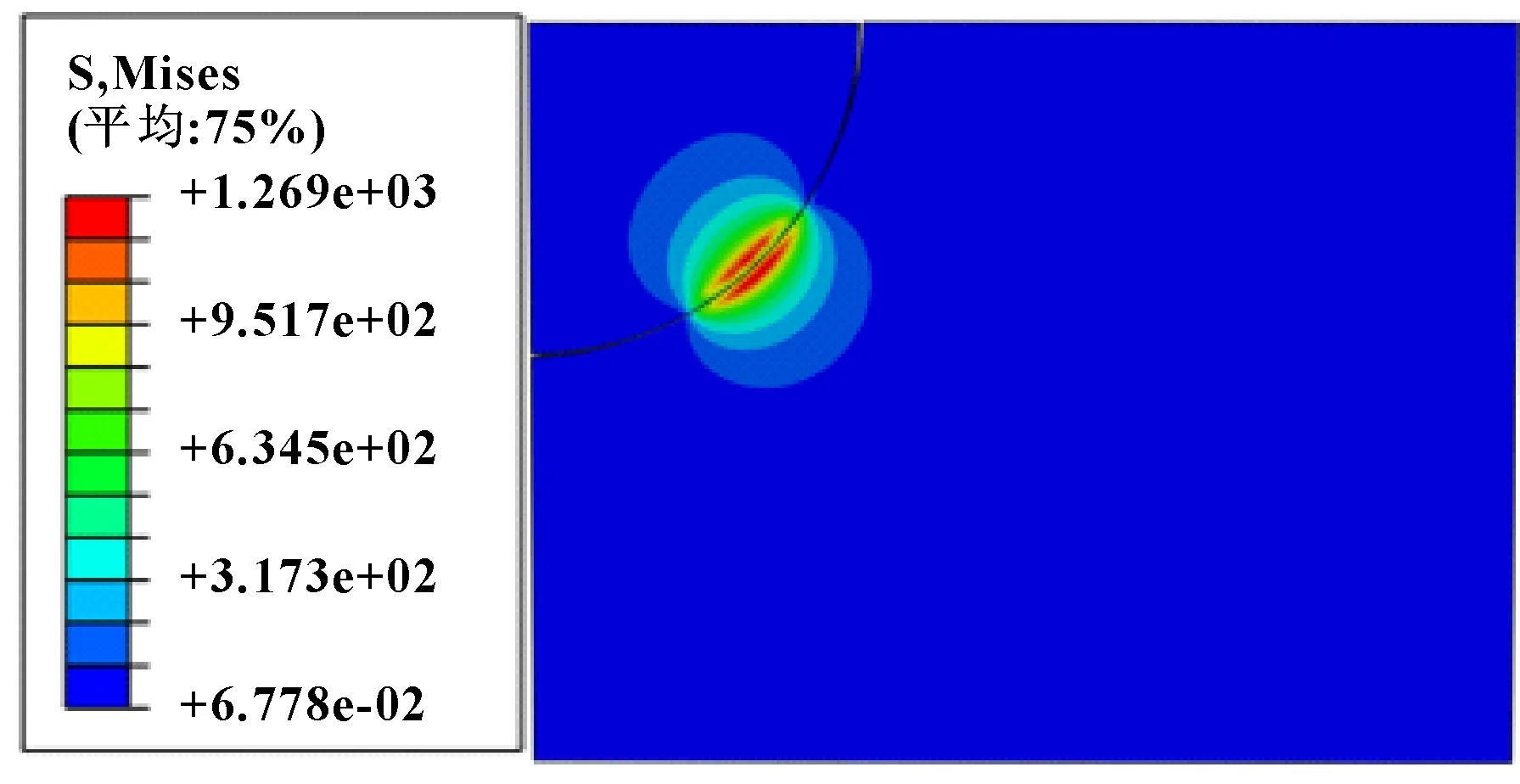
图13 钢球和滚道应力场(MPa)

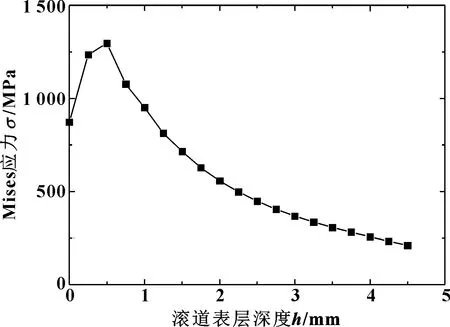
图14 滚道表层应力

2.2 滚道几何参数对应力分布的影响

轴承的几何参数如基圆内径、外径、钢球直径等已经标准化，而轴承接触角和滚道半径系数一般都是根据经验设计。但是，接触角和滚道半径系数对轴承承载能力产生影响。因此，有必要考察这些参数与轴承接触行为和疲劳寿命间的关系。

图15给出了不同参数下的应力分布，总体上，应力分布曲线变化趋势一致。而通过图15(a)和图15(b)可以看出，相比接触角对应力场的影响，不同滚道半径系数下的应力分布曲线层次更加明显，表明了滚道半径系数对应力场影响更显著。图16则给出了这2个参数下的最大应力值。由图16(a)可知，最大应力值随着接触角增大而减小，这是由于当接触角增大时，钢球与滚道接触点处所承受的法向分量的载荷值减小，所以在所施加的外载荷不变的情况下，最大应力值与接触角呈负相关关系。如图16(b)所示，最大应力值随着滚道半径系数的增大而增大。由于滚道半径系数是滚道半径与钢球直径的比值，滚道半径系数增大，钢球和滚道的接触面减小，甚至趋向于点接触形式，因此造成最大应力随滚道半径系数的增大而升高的现象。

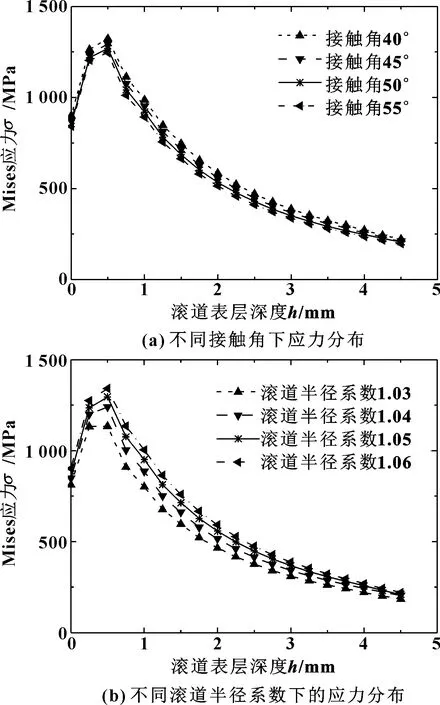
图15 不同参数下的应力分布情况

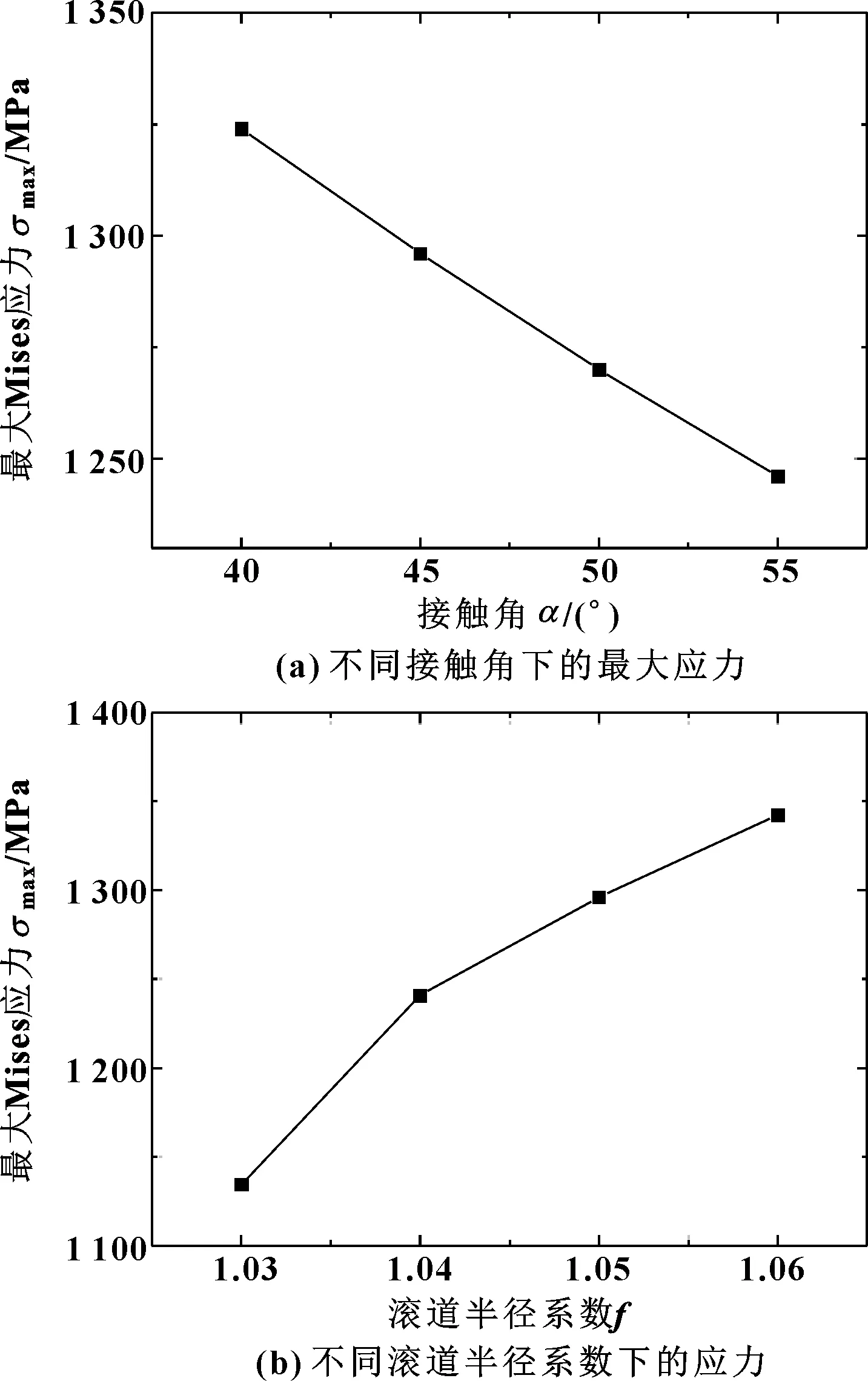
图16 不同参数下的最大Mises应力值

2.3 疲劳寿命分析

轴承滚道上几何参数的改变对接触区域的应力场产生影响，最终影响轴承的疲劳寿命，因此，接下来考察不同几何参数下轴承的疲劳寿命。分析中，采用Fe-safe疲劳计算软件进行轴承的寿命预测。

滚道材料为42CrMo，极限拉伸强度为1 080 MPa，弹性模量为207 GPa，屈服强度为930 MPa。Fe-safe的材料库中没有提供偏航轴承的材料参数，可根据轴承材料属性得到如图17所示的S-N曲线。另外，偏航轴承工作环境特殊，通常在小角度范围内运转。由于风速、风向和风力的影响，轴承滚道上承受交变应力，是造成疲劳损伤的主要原因。因此，滚道上的接触应力视为脉动循环应力，根据文献[18]中的载荷谱定义轴承的载荷信息，设置最大负载为1，最小负载为0，如图18所示。

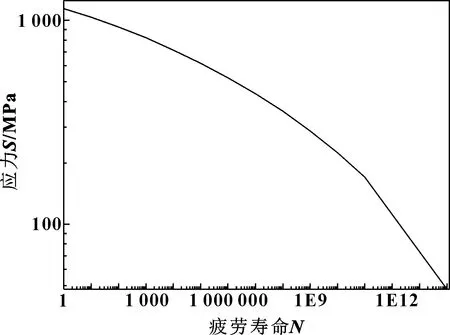
图17 42CrMo的材料属性

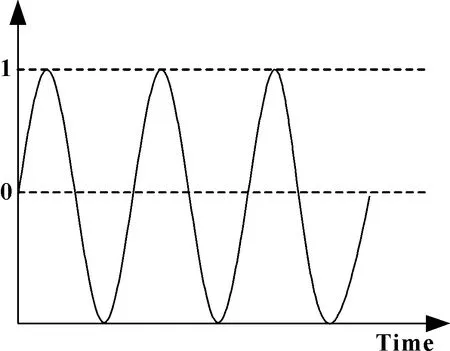
图18 载荷谱

疲劳寿命预估以轴承材料和应力为基础，并基于应力寿命理论进行疲劳损伤分析。根据应力寿命理论，疲劳寿命或应力循环次数N可通过以下方程[19]求得

(11)

式中：σ为等效疲劳应力;σ′f为疲劳强度系数;b为疲劳强度因子。

由于滚道上承受脉动循环的载荷，因此需要考虑平均应力的影响。基于Goodman平均应力修正原理，等效疲劳应力可表示为

(12)

式中：σa、σm是等效交变应力和平均应力;Rm是极限拉伸强度。

寿命分析结果如图19所示，可知接触角和滚道半径系数对轴承疲劳寿命产生了不同的影响。其中，疲劳寿命随接触角增大而提高，而滚道半径系数的增加会导致疲劳寿命的下降。

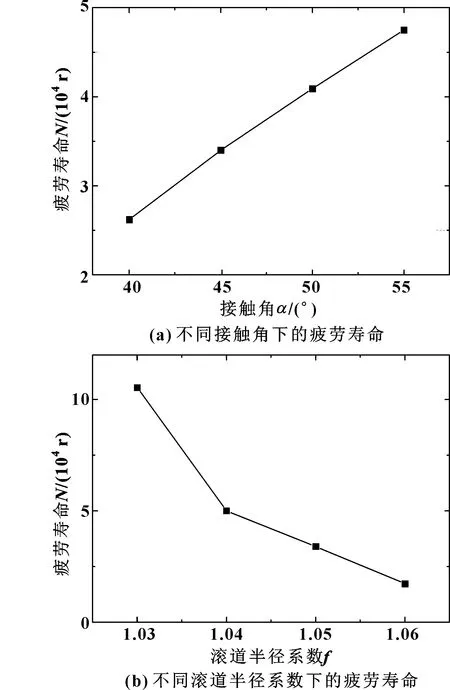
图19 不同参数下的轴承疲劳寿命

3 结论

基于有限元法获得了偏航轴承的接触力分布，通过静载实验验证了模型的正确性；构建钢球和滚道的等效接触模型，分析了接触角和滚道半径系数对接触应力场和疲劳寿命的影响。结论如下：

(1)采用等效有限元建模方法有效地降低了计算规模，提高了建模效率，适用于偏航轴承的接触力分布求解。

(2)不同的接触角和滚道半径系数下，滚道沿表层深度的应力分布基本一致，其中，滚道半径系数对应力分布的影响最显著。

(3)滚道最大Mises应力随接触角增大而减小，随着滚道半径系数的增大而增大，过高的滚道半径系数将降低轴承的承载能力。

(4)接触角和滚道半径系数对轴承疲劳寿命产生不同的影响，轴承疲劳寿命随接触角增大而提高，但随着滚道半径系数增大而下降，过大的半径系数对轴承疲劳寿命有负面影响。