径向动压气体轴承承载能力的CFD分析*

龚 霖 殷玉枫 张 锦，2 赵春江 柴晓峰 曾 光

(1.太原科技大学机械工程学院 山西太原 030024；2.山西交通职业技术学院 山西太原 030031)

随着高新技术的发展，对于旋转支撑轴承的要求越来越高，以润滑油为介质的滑动轴承和滚动轴承已经不能满足某些现代机械设备对于支撑轴承的需求，所以气体润滑轴承成为了最佳的选择[1]。其优点主要在于：具有摩擦损耗低，极高速度下几乎没有摩擦热、无磨损，极低运动速度下不会爬行，运动精度高，振动小，无污染以及在特殊工作条件下稳定运行的优点。与传统的轴承相比较，气体轴承使得转子速度提高了5～10倍，支撑精度提高了2个数量级，功率耗散情况降低了3个数量级，同时轴承的工作寿命增加了数十倍。因此，在精密工程、超精密工程、微细工程、空间技术、电子精密仪器、医疗器械及核子工程等范畴中，空气轴承有着十分广阔的应用前景[2]。

气体轴承按照是否需要外部气源分为静压气体轴承和动压气体轴承。其中静压气体轴承需要通过外接气源来使其形成静压气膜，支撑轴承悬浮于转子之上，其承载能力较大，同时精度也较高。但是外接气源使得轴承结构变得复杂，导致其制造与维护费用增大[3]。动压气体轴承也称为“自作用轴承”，它是不需要外部气体源并且仅在流体动力的作用下产生支撑作用的轴承[4]。动压气体轴承的特点是结构简单、精度较高、制造工艺复杂，适用于小型、轻载、高速精密支撑[5]。

目前国内气体动压轴承的设计与研究主要是采用MATLAB求解雷诺方程，其方法包括有限差分法、有限元法等。肖云峰等[6]研究了Sommerfeld数对气体动压轴承动力学特性参数的影响，包括对偏心率、最小气膜厚度、最大气膜压力、摩擦功耗、刚度和阻尼的影响。丁博等人[7]建立了一种具有特殊侧面结构混合式气体动压轴承的数学模型，分别推导出周向面和侧向面的雷诺方程，采用有限差分法对雷诺方程进行离散，通过MATLAB数值计算得出混合式气体动压轴承的稳态气膜厚度和气膜压力分布；采用复化辛普森积分法计算出量纲一承载力，分析偏心率、转速和压缩数对轴承量纲一承载力的影响规律。周秀文和孙长年[8]通过对圆柱轴承动压油膜流场雷诺方程的推导，在MATLAB软件中对雷诺方程采用有限差分法求解偏微分方程，获取动压油膜的相关动力学系数。

气体的压力场求解时，由于气体在轴承间隙的流动是一种相当复杂的三维流动，使用解析法求解承载能力的大小、分析压力分布情况极其困难，同时在计算的过程中需要作出一些假设，带来了计算误差[9]。又由于其计算需要进行编程，使得求解过程更加杂化。Fluent软件是一个用来模拟从不可压缩到高度可压缩范围内复杂流动的专用CFD软件，利用它可以准确地预测出气体流动实际的细节情况，如速度场、压力场、温度场、密度场的分布随时间变化的特性，并且还可以得到一些规律性的结论[9]。另外由于气体动压轴承的间隙属于微米级，对于试验来说动压气体轴承的加工精度要求和加工成本对其设计与制造有着极大的制约，而采用Fluent进行流体动力学分析，不需要进行编程计算，大大节约了设计时间，提高了工作效率，对于真实情况下的动压气体轴承的设计与制造具有指导意义[10]。

本文作者以径向气体动压轴承为对象，使用三维建模软件进行建模，并通过ANSYS自带网格划分软件ICEM进行网格划分建立有限元模型，利用CFD软件Fluent对径向气体动压轴承在稳态下的气膜压力进行分析，探讨偏心率和长径比对其承载力的影响。

1 径向动压气体轴承的结构

图1所示为径向动压气体轴承示意图，其轴承间隙为微米级。其中Ob为轴承的坐标中心，Or为轴颈的坐标中心，轴颈以角速度ω做逆时针运动，L为轴颈所受的外载荷，B为轴承的宽度，R为轴颈半径，φ为偏位角，h为轴颈外表面与轴承内表面之间的间隙，θ为极角[11]。若没有外载荷，轴颈中心Or与轴承中心Ob重合，一般情况下，轴颈总是承受一定的外载荷，因此两中心不会重合，其偏心距为e。

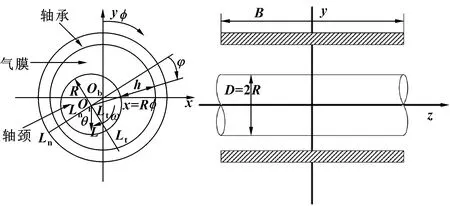
图1 径向动压气体轴承示意

2 雷诺方程的推导及求解

气体动压润滑分析的基本内容是以求解Reynolds方程来揭示气体润滑中压力的分布规律，轴承间隙内气体压力分布状况影响轴承的性能。在考虑润滑层内流动的边界层特性和流动的连续性，以及气体所满足的状态方程出发进行稳态情况下二维可压缩气体润滑Reynolds方程的推导[12]。

由于气体动压润滑具有特殊性，通常情况下分析气体动压润滑需要做以下假设：

(1) 与轴承的长度和宽度相比，气膜的厚度很微小，因此可以假设轴承表面为平面；

(2) 沿气膜厚度方向，其压力的变化可以忽略不计；

(3) 与黏性剪应力相比，流体的惯性力可以忽略不计；

(4) 气体流动状态为层流；

(5) 润滑表面上气体与壁面间没有相对滑动；

(6) 气体温度为常数[13]。

Navier—Stokes(N-S)方程作为气体润滑基本方程之一，在Descartes坐标系中的表达式为

(1)

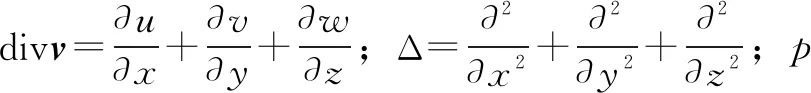
根据质量守恒原理(单位时间内由微元体流出的总质量与微元体内质量的变化率相等)可得，气体连续性方程的表达式为

(2)

气体状态方程为

(3)

式中：R为气体常数；T为气体绝对温度。

由于气体的黏性很小，气体在轴承间隙中流动的过程中由摩擦产生的热量可以忽略，因此在气体动压轴承工作的过程中，可以认为气体是等温的。因此，由气体状态方程可得：

(4)

式中:pa为大气压力；ρa为大气压力下的气体密度；C为常数。

结合上文给出的假设，可以将N-S方程简化为以下形式：

(5)

令边界条件为

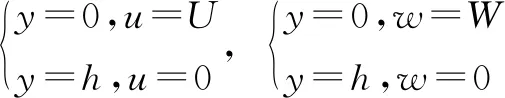
通过积分可以将N-S方程中沿x轴方向的速度和沿z轴的速度分别求解出来，即：

(6)

将由N-S方程式推出的运动方程、连续性方程和气体状态方程结合起来，经过一系列的推导过程得出

(7)

式中:μ为气体的黏度(Pa·s);h为动压气膜厚度；t为时间；U为轴颈与轴承外圈之间相对速度沿着x轴的速度分量；W为轴颈与轴承外圈之间相对速度沿着z轴的速度分量。

方程(7)即为二维可压缩流体的动压润滑方程——雷诺方程。

恒温稳定工况下，气体动压润滑Reynolds方程的量纲一化的形式为

(8)

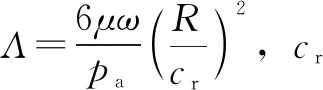
因为

(9)

(10)

(11)

因此，经上述变换，气体动压润滑量纲一化稳态雷诺方程(8)变为

(12)

在气膜求解区域中，使用有限差分法求解动压气体润滑轴承的压力分布时，根据步长Δφ、Δλ进行网格划分，从而在给定区域中存在(N+1)(M+1)个网格点。分别使用每个节点上的压力进行组合形成一阶和二阶的差商，近似地替代雷诺方程中的偏导数，将雷诺方程离散化为一组线性代数方程，该线性代数方程的解Pi,j就是气膜的压力值[14]。在气膜区域中对所求压力值进行相应地数值积分，以获得诸如承载能力、阻力和流量之类的性能值[15]。图2所示为气膜区域网格划分图。

图2 气膜区域网格划分

求解气膜区间中压力分布的具体方法如下：先将网格点按照所在的列和行顺序进行编号，沿φ方向的列用i编号，沿λ方向的行用j编号，每个节点的位置用(i,j)二维编号表示；设在φ方向均分为N格，i的编号从0到N，每格宽度(步长)为Δφ=(φ2-φ1)/N;在λ方向上均分为M格，j的编号从0到M，步长Δλ=(λ2-λ1)/M，节点(i,j)上的P值以Pi,j表示。

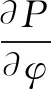
(13)

(14)

(15)

(16)

相对应的气膜厚度的一阶中差商可以近似地表述为

(17)

(18)

按照差分原理，将差分格式(13)—(18)代入式(12)，可以得到动压气体润滑稳态雷诺方程的量纲一化差分形式，然后求解关于Pi,j的线性方程(舍去负值)，进而整理得到关于网格点(i,j)对应的压力值[16]为

(19)

其中，

(20)

根据求得的压力分布值，采用复化Simposion积分法沿轴承面进行积分,可得轴承径向和切向量纲为一的气膜力为

(21)

因此得到量纲为一的气膜承载力为

(22)

3 气体动压轴承特性的CFD分析

3.1 物理模型的建立

分析轴承的静态性能，主要是分析轴承间隙中的压力分布情况、气膜承载能力的大小，因此将轴承与轴颈之间的流体作为研究对象，建立三维模型。由于轴承与轴颈中心不在同一个圆心，导致所需流体域并非一个规则的薄壁圆筒，而是上边厚下边薄的不规则薄壁圆筒，因此不能够直接进行建模。文中采用三维建模软件Solidworks对径向动压气体轴承进行物理建模[17]，如图3所示;然后通过ANSYS有限元分析软件自带的DM(Design Modeler)提取流体域，如图4所示。

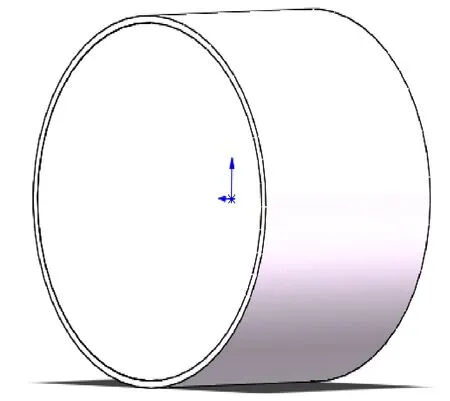
图3 径向动压气体轴承的物理模型

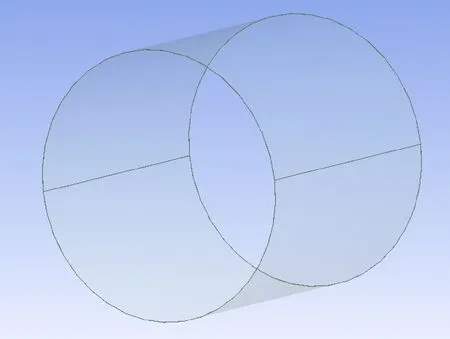
图4 径向动压气体轴承的计算流体域

3.2 网格划分及边界条件设置

有限元分析软件ANSYS中自带的网格划分软件Mesh和ICEM分布适用于划分非结构网格和结构网格，非结构网格其单元为正四面体和三角形，而结构网格其单元为正六面体和四边形。非结构网格划分简单，但是其网格质量一般不是很好，同时其计算时间长。结构网格的划分先需要分块，然后对各个点、线、面进行关联，因此其操作复杂，但是所生成的网格质量较高，网格数量和计算时间都优于非结构网格[18]。

由于所提取流体域的厚度与其他参数相比小得多，如果使用非结构化网格划分，其质量较低，网格数量庞大，计算时间过长。因此文中选用结构网格进行划分，运用ICEM来完成网格的划分。网格划分如图5所示。

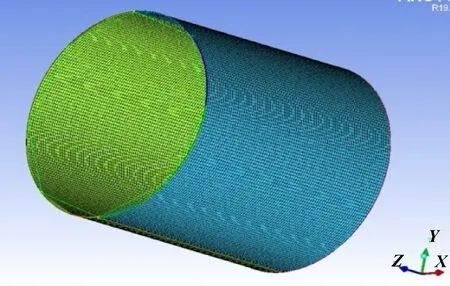
图5 网格划分

为了验证网格数量对于实验结果的影响，文中就不同的网格密度进行了仿真计算，结果如表1所示。可以看出，不同网格数量对于最大压力与承载力的影响很小，但是计算时间却是成倍增加，即网格数量越大，所需的计算时间越长。并且网格数量过大会导致轴承最小气膜厚度附近的网格出现畸形，从而导致网格质量下降，影响计算结果的准确性。因此文中选择网格的数量为175 961，既保证了计算结果的准确性又缩减了计算时间。

表1 网格数量对计算结果的影响

对于边界条件的设置同样可以在ICEM中完成，其中将外圈设置为固定壁面，内圈设置为移动壁面，其速度值为轴颈的旋转速度，而两侧设置为压力出口条件，其压力值为一个大气压。边界条件示意图如图6所示。

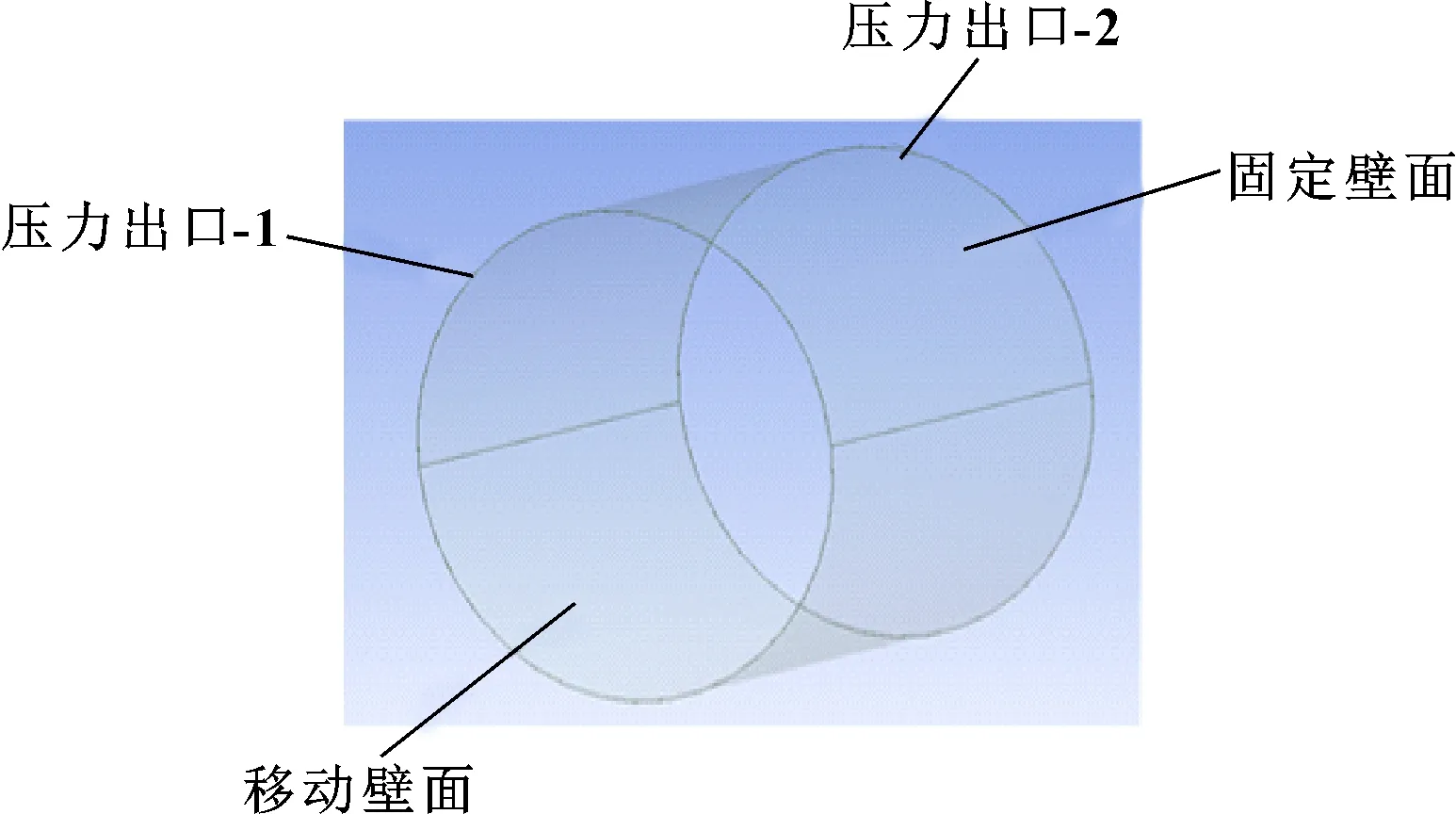
图6 边界条件示意

4 仿真结果及验证

轴承的承载力主要是由于轴承存在偏心，使得轴承内部的气膜厚度不同，又因为润滑介质为可压缩气体，因此气膜厚度最小处存在最大压力，而在气膜厚度最大处存在最小压力，形成压力差，从而使得气体动压轴承具备了承载能力。偏心率对于轴承内部的压力差大小具有显著的影响，偏心率越大，轴承内部压力差越大，轴承的承载力也越大。长径比主要是表示轴承承载面积的大小，长径比越大，轴承承载面积越大，承载能力相应地越大。对于轴承的承载力而言，偏心率和长径比是主要的影响因素，因此文中主要研究偏心率和长径比对轴承承载力的影响。

研究的径向动压气体轴承的模型参数如表2所示。

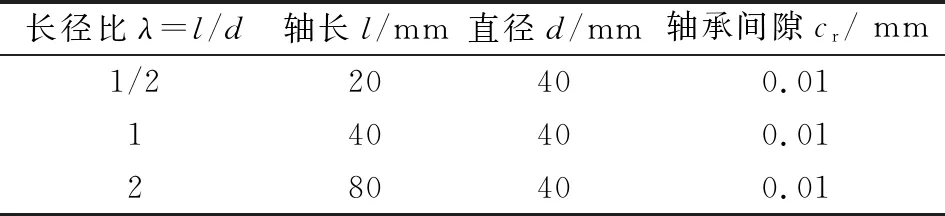
表2 模型参数

4.1 仿真结果及分析

在转速15 000 r/min下，按表2中参数计算不同长径比和偏心率情况下轴承的压力分布，分别如图7、8所示；计算不同长径比和偏心率情况下轴承的承载能力，分别如图9、10所示。

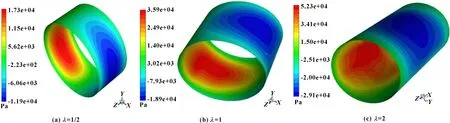
图7 偏心率为0.2、转速为15 000 r/min时不同长径比下气膜压力分布云图

图8 长径比为1/2、转速为15 000 r/min时不同偏心率下气膜压力分布云图

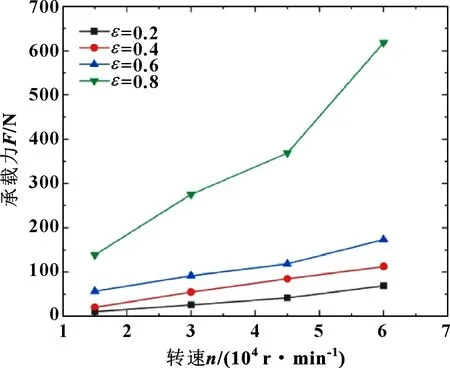
图9 长径比为1/2时不同偏心率下轴承承载力随转速的变化

从图7、8可以看出，轴承整体气膜的压力分布沿轴承轴向中线几何对称，由于轴承的偏心作用，在轴承最下端为气膜最薄的区域即收敛的楔形空间，气体流入的方向，正压力达到了最大，而在气体流出的方向上，负压达到了最大值，在气体动压轴承偏心的区域两端出现最大的压差，以平衡轴承外载荷的作用，从而使得气体动压轴承具备了一定的承载能力。而在轴承两端，其压力与环境压力大致相等。在不同的长径比、转速以及偏心下，其压力分布规律都大致相同。

由图 9可以看出，当长径比一定时，随着偏心率的增大，轴承的承载力也随着增大；当偏心率较小时，轴承的承载力随着转速的增大幅度较小，而当偏心率较大时，轴承的承载能力随着转速的提高有了一个较大的提升，且增长规律呈非线性。由于承载力等于轴承整个润滑膜上的压力差，且气体为可压缩流体，因而当偏心率增大时，气体间隙最小处的气体密度增大，压力增大，相反气膜间隙最大处的密度减小，气体压力也减小，则二者的压力差增大，使得轴承的承载力增大。

由图10可以看出，当偏心率一定时，随着长径比的增大，轴承的承载能力随着转速的变化呈现出非线性上升趋势；而且长径比越大，轴承的承载能力随转速变化趋势越明显。由于轴承长径比的增大，使得轴承的承载面积增大，因此在相同的压力差下，其承载力也明显增大。

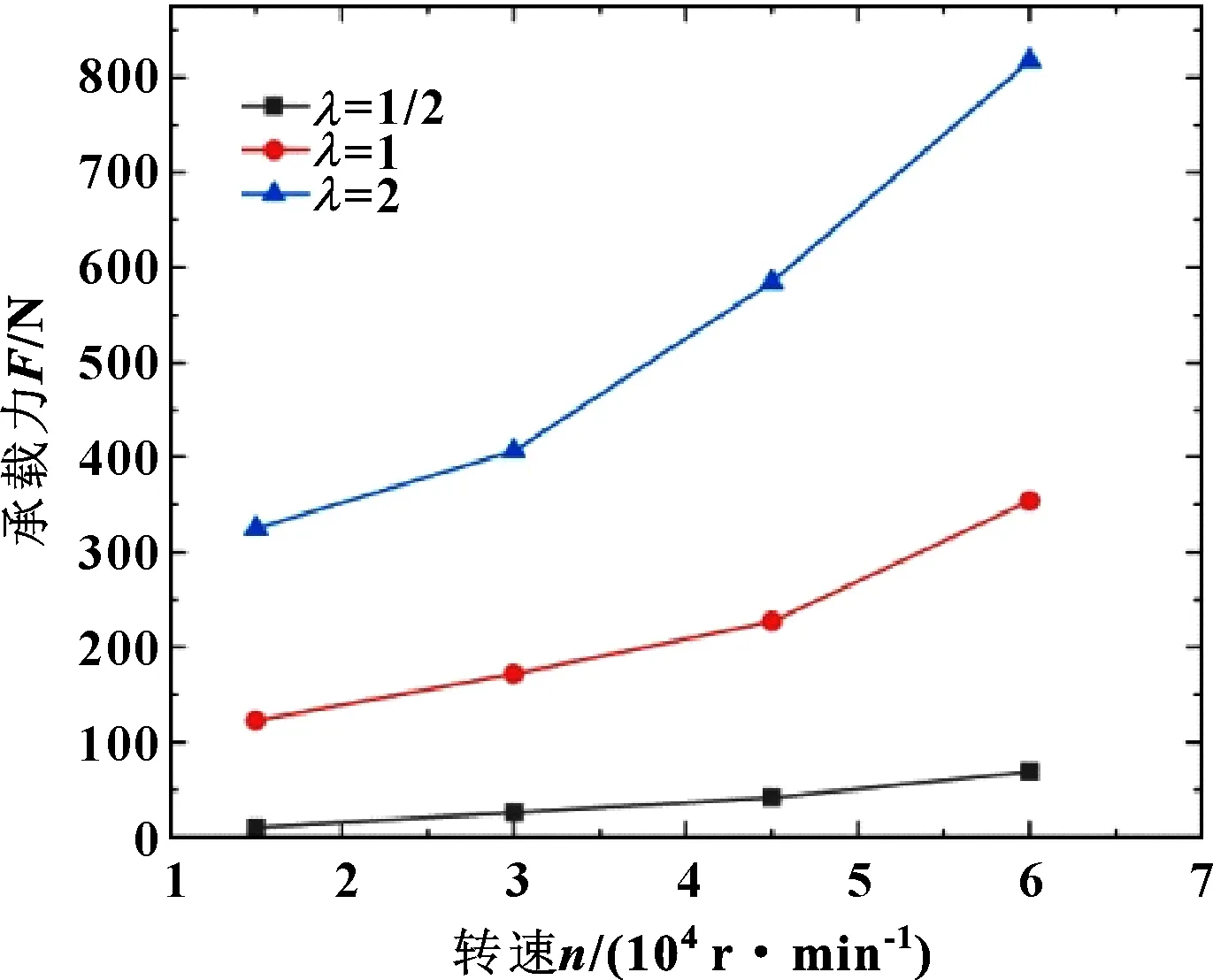
图10 偏心率为0.2时不同长径比下轴承承载力随转速的变化

4.2 验证

为了验证文中计算结果的正确性，图11给出了文献[1]中不同偏心率下长径比对承载力影响的计算结果，图12给出了文献[19]中不同偏心率下转速对轴承承载力影响的计算结果。通过对比文献[1]中的计算结果图11与文中的计算结果图10，可以明显看出，两者承载力曲线大致相同，因此验证了文中长径比对轴承承载力影响的计算结果的正确性。对文献[19]中的计算结果图12与文中的计算结果图9，验证了文中偏心率对轴承承载力影响的计算结果的正确性。

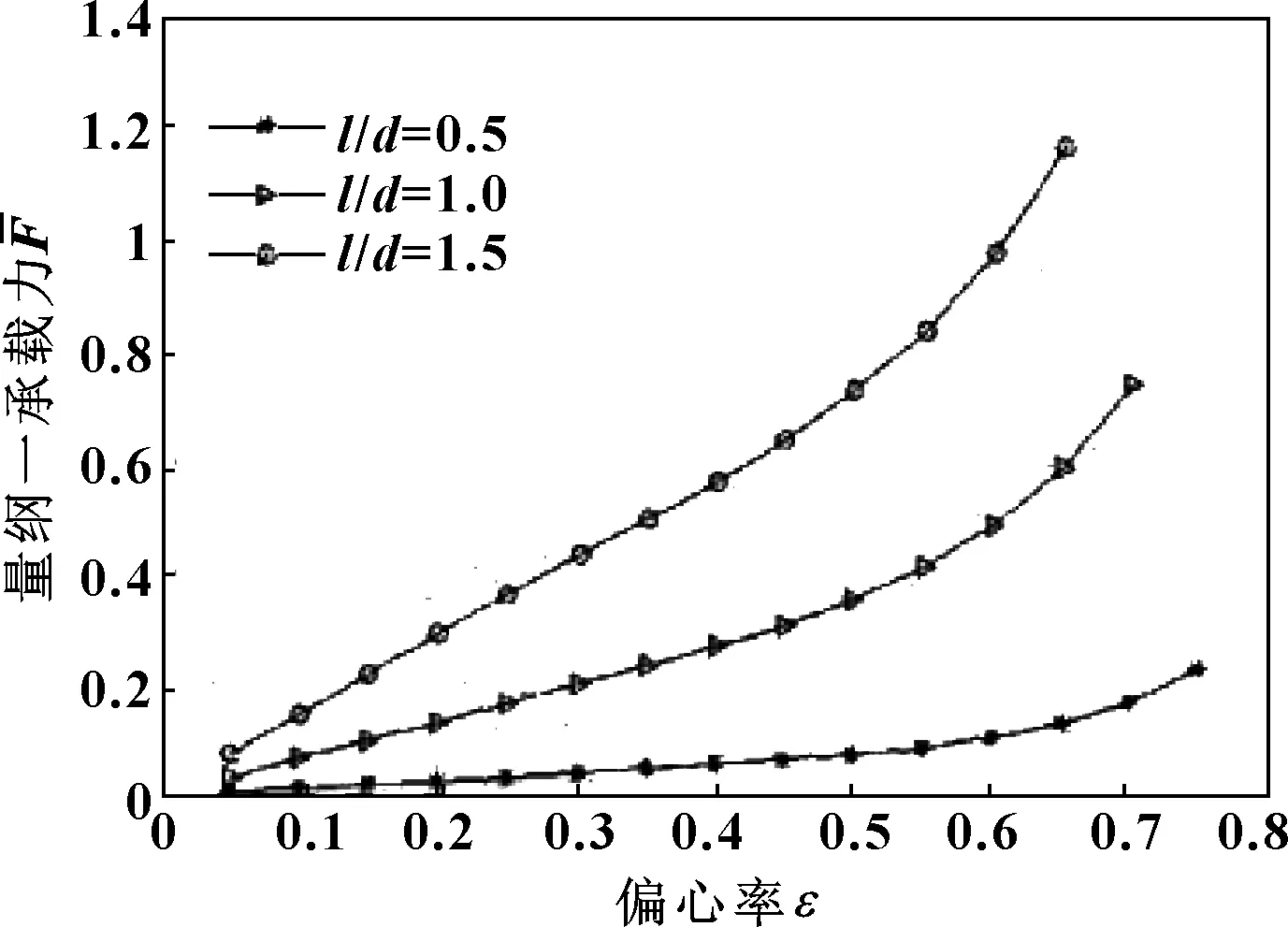
图11 文献[1]中不同长径比下偏心率对承载力的影响

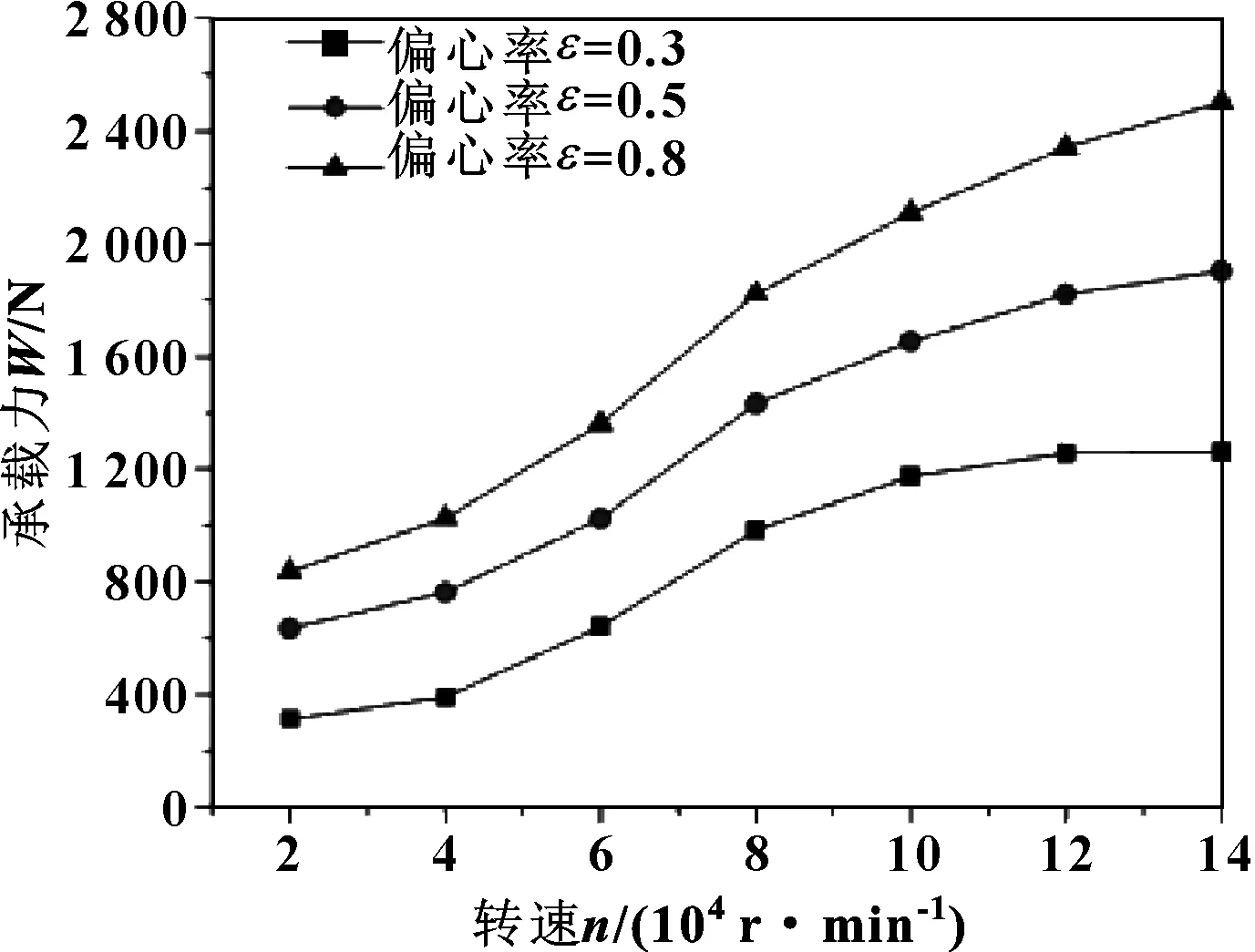
图12 文献[19]中不同偏心率下转速对轴承承载力的影响

5 结论

基于Fluent对空气动压轴承进行有限元仿真，得出其在运行过程中的气膜压力分布云图，分析了在不同偏心率和长径比下轴承的承载能力随着转速的变化规律。主要结论如下：

(1)轴承整体气膜的压力分布沿轴承轴向中线几何对称，由于轴承的偏心作用，在轴承最下端为气膜最薄的区域；气体流入方向存在正压最大区域，气体流出方向存在负压最大区域，由于气体的压差使得轴承具有了一定的承载能力。

(2)当轴承的长径比一定时，随着偏心率的增大，轴承的承载能力随转速增大的趋势越明显，其增长趋势呈非线性规律。

(3)当轴承的偏心率一定时，随着长径比的增大，轴承的承载能力随转速增长的趋势也越明显，其增长趋势也呈非线性变化规律。