基于流固耦合的橡胶O形圈密封泄漏计算方法*

吴 凡 郭 飞 高 燕 项 冲 黄 乐 贾晓红

(1.清华大学摩擦学国家重点实验室 北京 100084；2.广州机械科学研究院有限公司，国家橡塑密封工程技术研究中心 广东广州 510700)

橡胶O形圈具有良好的弹性和回弹性，且结构简单、尺寸紧凑，适用压力、温度范围广，是一种常用的静密封形式[1]。

从宏观角度看，只要提供足够的初始预紧力，保证密封面最大接触压力大于密封介质压力，密封面就不会发生泄漏。对于橡胶O形圈密封，介质压力越大，密封面的最大接触压力越大，可实现自紧密封。但从微观角度看，由于橡胶表面微观粗糙形貌的存在，接触压力大于介质压力时泄漏通道也是不可避免的，因此以泄漏率为参数更能有效地表征橡胶O形圈的密封性能。

目前，针对橡胶O形圈密封性能的理论研究多以有限元仿真为主，以最大接触压力表征密封性能。陈志等人[2]、关文锦等[3]、WEI等[4]对不同介质压力、不同预压缩率、不同硬度的橡胶O形圈密封的Mises应力、接触应力、接触宽度等进行了有限元仿真分析。陆婷婷等[5]以黏弹-超弹组合模型作为橡胶材料本构模型，分析了黏弹性导致的应力松弛对密封面接触压力的影响。张镇国等[6]基于有限元仿真研究了双道O形圈静密封的密封性能。AKULICHEV等[7]、ALBRECHT和ACHENBACH[8]在有限元仿真中考虑了温度的影响。周池楼[9]以热传导分析方法分析等效浓度场作用下的氢传输扩散过程，在有限元中考虑了橡胶O形圈在氢环境下的吸氢膨胀效应。

尽管目前已有用于计算静密封泄漏率的模型，如平行平板模型[10]、Roth模型[11-13]、平均流量模型[14]、多孔介质模型[15-16]、栅格渗漏模型[17]、单枢纽泄漏模型[18]等，但将泄漏模型用于橡胶O形圈密封泄漏率计算的研究较少。一个主要的原因在于，上述模型均假设通道截面高度沿泄漏方向不变。对于橡胶O形圈密封，由于接触压力的非均匀分布，通道截面高度沿泄漏方向是变化的。因此，有必要对现有的泄漏模型进行改进，以适用于橡胶O形圈密封的泄漏率计算。

本文作者提出了一种基于流固耦合的橡胶O形圈静密封泄漏计算方法。对平行平板泄漏模型进行了改进，使其适用于通道截面高度可变的泄漏率、介质压力计算；采用有限元仿真方法进行固体力学分析，求解宏观接触压力；采用Greenwood-Williamson(GW)模型进行接触力学分析，求解泄漏通道平均高度。基于上述数值方法研究了介质压力、环境温度、表面形貌参数对橡胶O形圈密封性能的影响规律。

1 泄漏求解思路

图1为橡胶O形圈密封的泄漏求解示意图。对于橡胶O形圈密封，根据结构的轴对称特性，认为泄漏通道截面高度沿泄漏方向变化，沿接触长度方向不变。沿泄漏方向将泄漏通道平均划分为n个微单元，当单元数量足够多时，认为每个单元对应的截面高度恒定。截面高度由单元宏观接触压力psc和粗糙峰接触压力pcon、流体压力pf的受力平衡确定[19]。泄漏通道截面高度确定后，可由平行平板模型求解泄漏率。

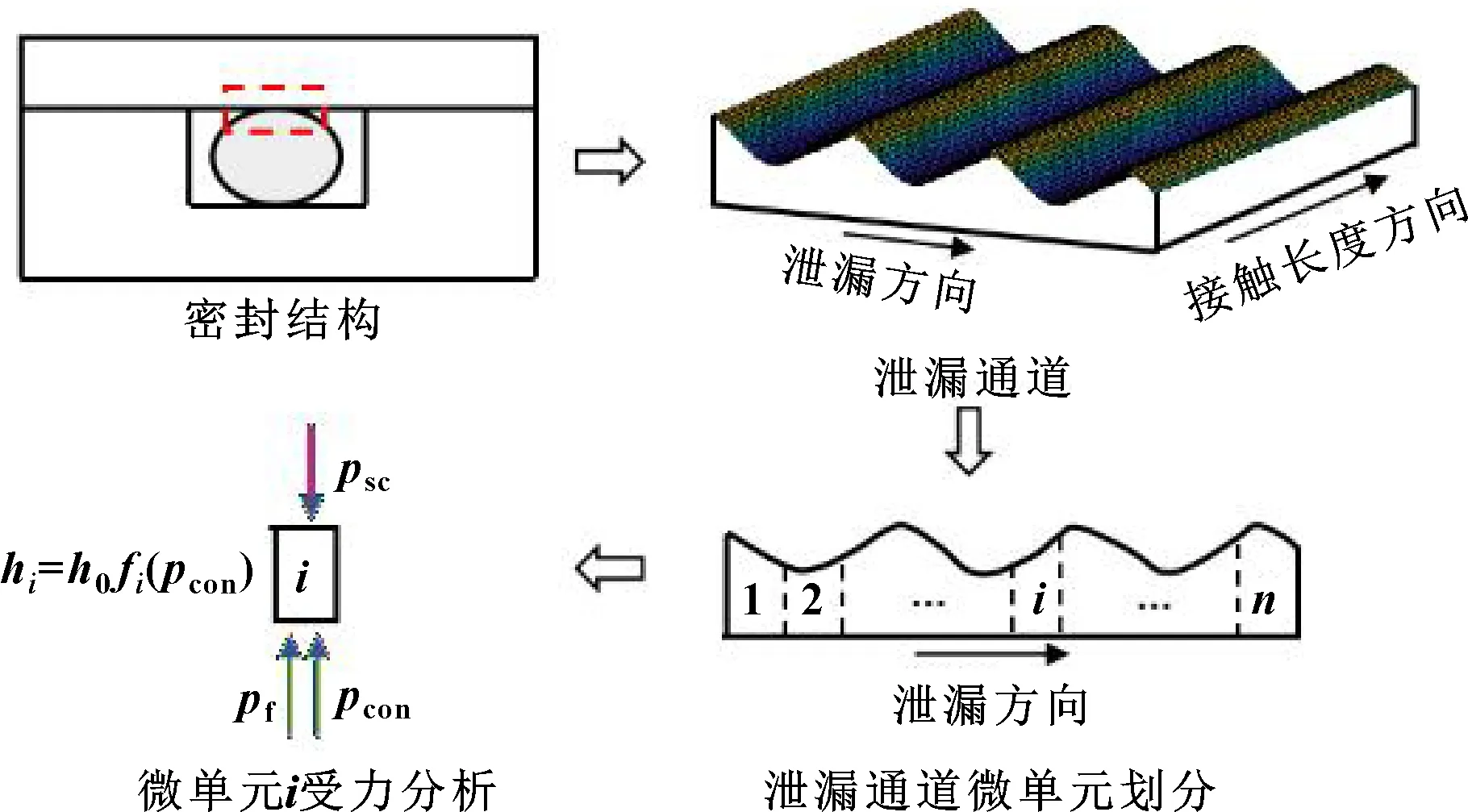
图1 泄漏求解示意

1.1 泄漏模型

对平行平板模型进行改进，使其适用于通道截面高度可变的泄漏率计算及流体压力分布pf的求解。

如图2所示，沿泄漏方向将泄漏通道平均划分为n个微单元，第i个微单元的截面高度为hi，单元两端介质压力为pi和pi+1。对于不可压缩黏性流体，流动遵循体积守恒，可由平行平板模型求解微单元体积泄漏率：

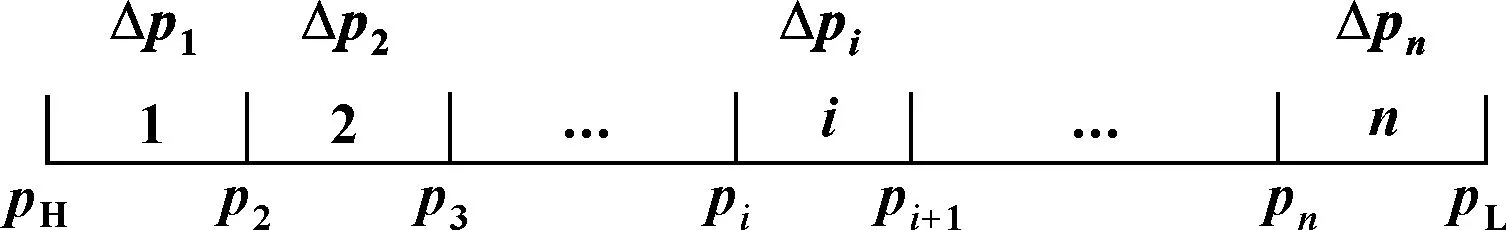
图2 流体压力分布

(1)

(2)

式中:h0为通道初始高度；fi为转化系数，其值为第i个截面高度hi与初始高度h0的比值；q为体积泄漏率;Δl为微单元通道长度;L为泄漏长度;b为通道宽度;d1为O形圈内径;μ为流体动力黏度。

由式(1)(2)知，每个微单元两端介质压差：

(3)

整个泄漏通道介质压差：

(4)

对应泄漏率表达式为

(5)

当n→∞时，式(5)可表示为

(6)

由式(5)或式(6)可看出，与原平行平板模型相比，改进后的模型泄漏率表达式中含有与通道截面高度分布相关的无量纲参数k。将泄漏率q代入式(3)可求解介质压力分布。

1.2 有限元模型

利用商用软件ABAQUS，建立O形圈密封有限元仿真模型，用于求解宏观接触压力psc。

建立图3所示的二维轴对称模型。装配体由O形圈、盖板、沟槽组成。其中，O形圈为橡胶材料，沟槽和盖板为钢结构。由于钢材料的弹性模量远大于橡胶材料，因此为减少计算量，将盖板和沟槽设为解析刚体。结构尺寸如表1所示。

图3 O形圈装配示意

表1 装配体结构尺寸

选择3阶Ogden模型作为橡胶材料本构模型，对橡胶材料的拉伸、压缩应力应变曲线进行拟合，拟合参数如表2所示。橡胶的拉伸断裂强度约为12.8 MPa。此外，根据橡胶的不可压缩性，设置泊松比为0.49。设置橡胶的热膨胀系数为1.15×10-4℃-1。

表2 3阶Ogden模型拟合参数

O形圈在压缩变形过程中会与沟槽、盖板接触，因此需分别设置接触相互作用，接触设置中摩擦因数设置为0.4，法向设置为“硬接触”。

整个仿真过程可分为4个过程。①O形圈扩张过程：根据初始状态，沟槽沿径向向外移动，以模拟O形圈装到沟槽上时的扩张过程；②预压缩过程：盖板向下移动模拟预压缩过程，根据移动距离控制预压缩率的大小，文中保持预压缩率为27.63%；③变温过程：施加相应的温度场，在变温过程中材料产生热胀冷缩；④施加介质压力过程：采用压力渗透法施加介质压力。

综合考虑橡胶的不可压缩性和接触问题，选取四节点线性轴对称杂交单元CAX4RH和三节点线性轴对称杂交单元CAX3H进行网格划分。网格划分的质量对计算结果的收敛性有很大影响。在仿真过程中，O形圈的外圈接触位置会发生较大变形，因此对O形圈进行分区，外圈网格适当加密以保证收敛。最终网格划分结果：外圈种子间距为0.02 mm，内圈种子间距为0.05 mm，网格数共8 232个。

1.3 粗糙峰接触模型

采用粗糙峰接触模型，根据粗糙峰接触压力pcon，求解泄漏通道平均高度。

GW模型[20]是一种常用的统计学模型。在GW模型中，假设各个微凸体的曲率半径都为R，z为微凸体高度，且服从高斯分布，d为微凸体平均高度与刚性平面间的分离距离，即泄漏通道平均高度。若忽略微凸体间的相互作用，则根据Hertz接触理论，平均接触压力pcon、量纲一接触面积A/An可表示为

(7)

(8)

(9)

式中：η为微凸体面密度；E为橡胶的弹性模量;ν为橡胶的泊松比;R为微凸体的曲率半径;Φ(z)dz为微凸体高度分布函数;σ为标准差即表面均方根偏差;A为实际接触面积;An为名义接触面积。

1.4 流固耦合

根据粗糙峰接触模型，粗糙峰接触压力分布会影响密封界面泄漏通道平均高度分布；根据静密封泄漏模型，泄漏通道平均高度分布会影响介质压力分布；根据受力平衡，介质压力分布会影响粗糙峰接触压力分布。综上，需进行流固耦合处理，得到整个密封界面泄漏通道平均高度及介质压力分布情况。

采用如图4所示的数值迭代方法进行流固耦合分析。根据有限元仿真模型求解宏观接触压力分布；初始情况设置介质压力为线性分布，令粗糙峰接触压力分布等于宏观接触压力与介质压力之差，根据粗糙峰接触模型求解泄漏通道平均高度分布；根据泄漏模型求解介质压力分布；更新粗糙峰接触压力为宏观接触压力与介质压力之差，再次进行接触力学分析和流体力学分析，直至介质压力及粗糙峰接触压力分布收敛。

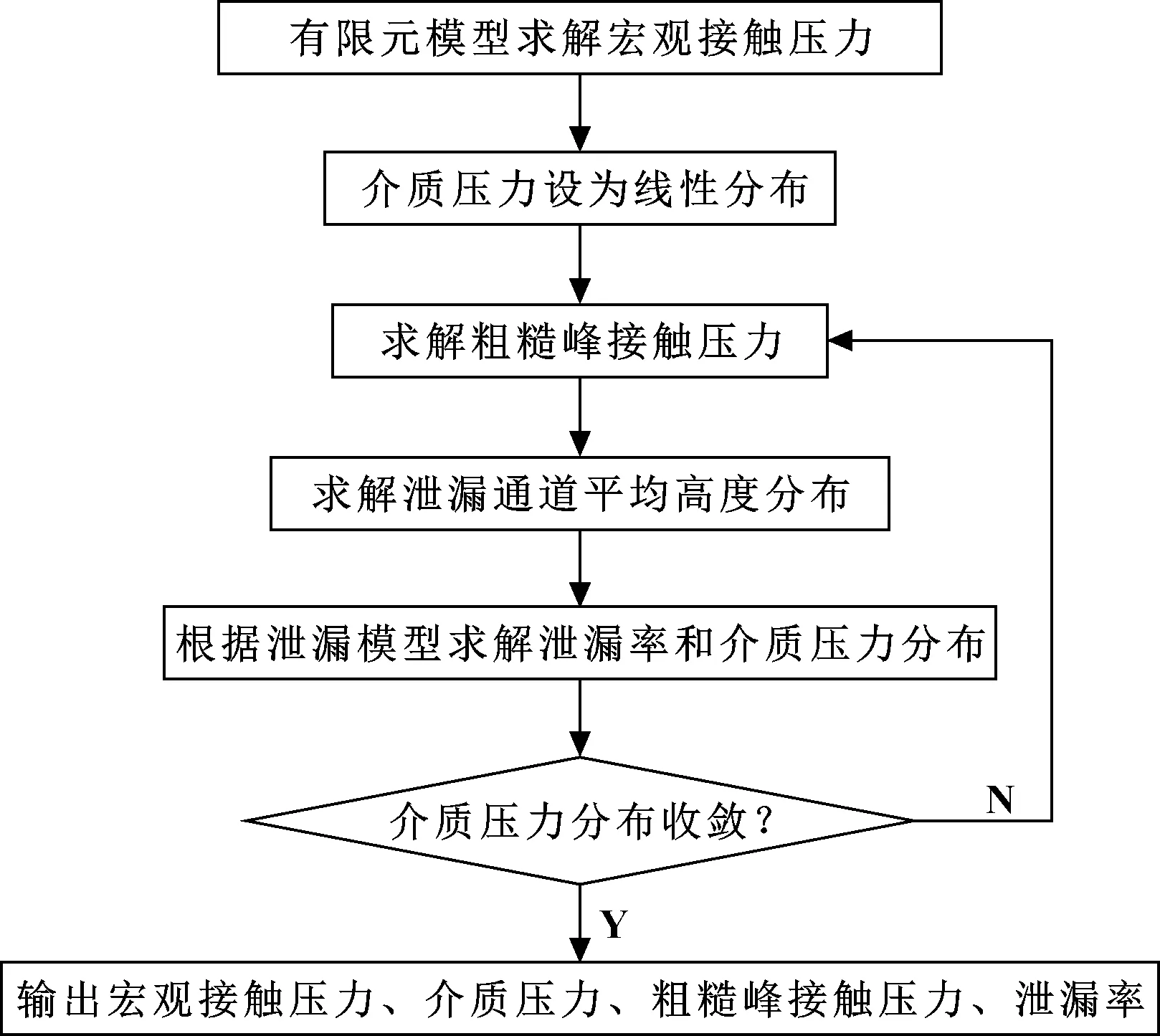
图4 数值迭代流程

1.5 方法验证

根据文献[21]的实验测试结果对文中的数值方法进行验证。光滑密封圈与粗糙的砂纸基底接触形成密封界面。其中密封圈为矩形截面，因此宏观接触压力psc沿泄漏方向为均匀分布。密封圈弹性模量为2.3 MPa，内圈直径为3 cm，外圈直径为4 cm，截面宽度为0.5 cm，截面高度为0.5 cm。砂纸基底的均方根粗糙度为44 μm，表面微凸体面密度为1.2×108m-2，微凸体曲率半径为45.7 μm。密封介质为水，水的常温动力黏度为8.9×10-4Pa·s。

根据文中的数值方法分别求解不同介质压差、不同宏观接触压力下的体积泄漏率，并与实验结果进行对比，结果如图5、6所示。可以看出，数值方法计算结果与实验测试结果接近：随着介质压差的增大，泄漏率近似线性增大；随着宏观接触压力的增大，泄漏率近似指数下降。因此，认为文中的数值方法具有一定的精确性。

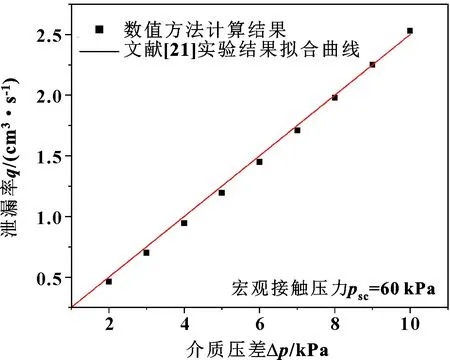
图5 泄漏率随介质压差变化规律

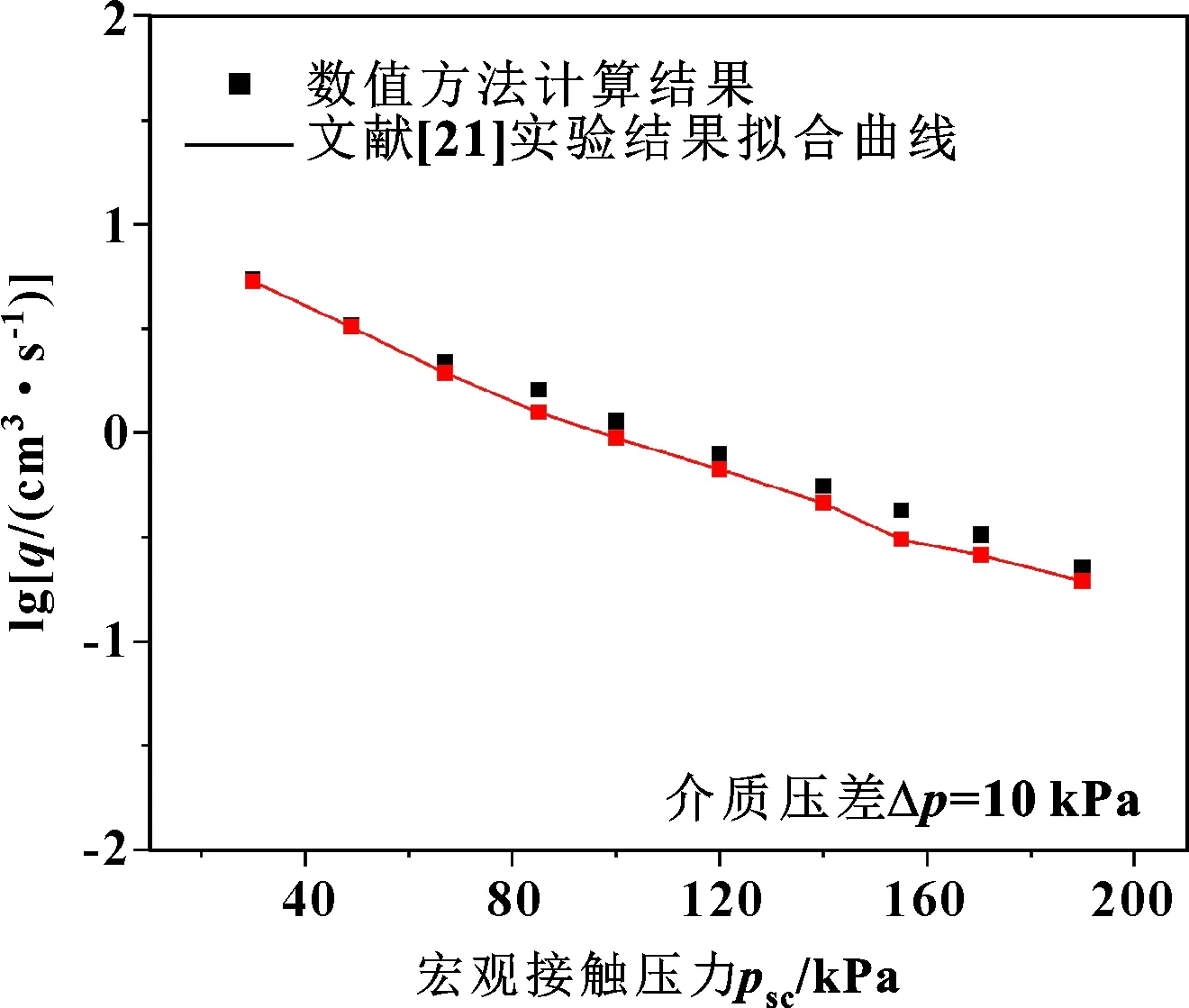
图6 泄漏率随接触压力变化规律

2 结果与分析

根据上述数值方法对橡胶O形圈密封进行分析，研究介质压力、温度及表面形貌参数对O形圈密封性能的影响规律。

2.1 介质压力的影响

在有限元仿真分析中，保持环境温度为25 ℃，设置高压侧介质压力分别为0.2、0.4、1、2、5 MPa，低压侧介质压力为大气压。研究最大Mises应力和最大接触压力、接触宽度随介质压力的变化规律，结果如表3所示。

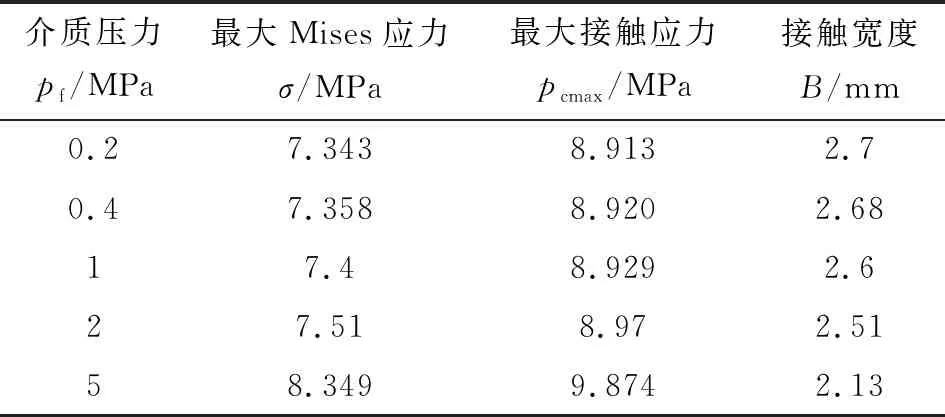
表3 不同介质压力下应力及接触宽度计算结果

可以看出，橡胶O形圈具有自紧密封作用，即随着介质压力的增大，主密封面的最大接触压力增大，且始终大于介质压力。因此宏观上讲，O形圈具有较好的密封性能。另一方面，随着介质压力的增大，最大Mises应力逐渐增大，但始终小于拉伸断裂强度12.8 MPa，因此不会出现断裂失效。

提取不同介质压力下的界面宏观接触压力分布，结果如图7所示。

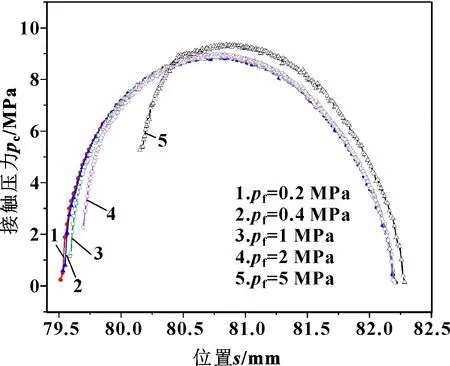
图7 不同介质压力下接触压力分布

橡胶力学参数、表面形貌参数及密封介质(油)参数分别如表4、表5所示。根据上述数值方法求解不同介质压力下的泄漏率，结果如图8所示。可以看出，随着介质压力的增大，体积泄漏率逐渐增大。以5 MPa下计算结果为例，如图9所示，介质压力由高压侧至低压侧逐渐减小，根据宏观接触压力与粗糙峰接触压力、介质压力的受力平衡，粗糙峰接触压力先增大后减小，对应泄漏通道平均高度先减小后增大，通道高度在0.8～2.7 μm范围内。

表4 橡胶参数

表5 不同温度下密封介质黏度

图8 体积泄漏率随介质压力变化规律

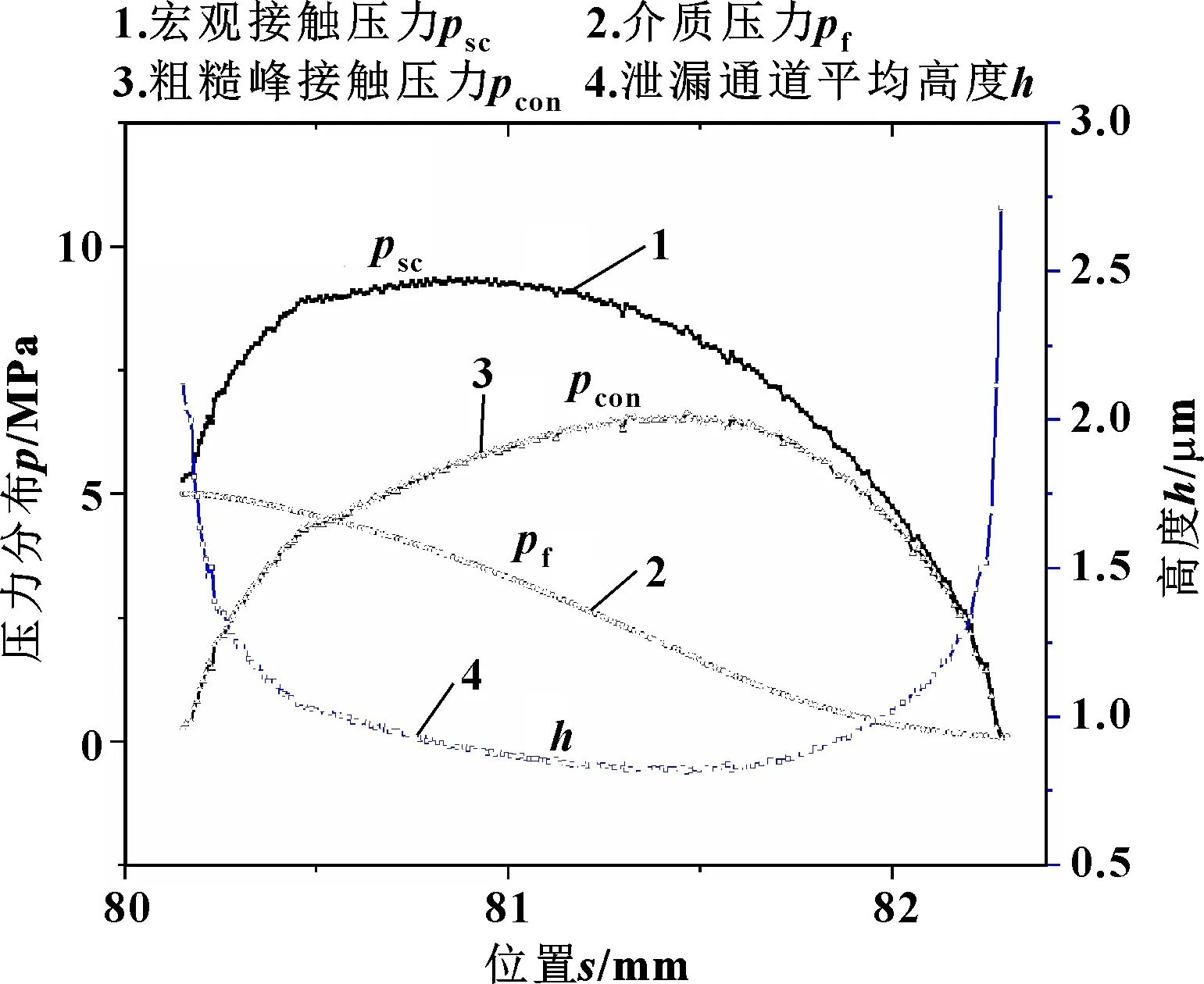
图9 介质压力5 MPa下压力、高度分布

2.2 温度的影响

在有限元仿真分析中，保持高压侧介质压力为0.4 MPa，设置环境温度分别为0、25、60、100、140 ℃，研究最大Mises应力和最大接触压力、接触宽度随环境温度的变化规律，结果如表6所示。

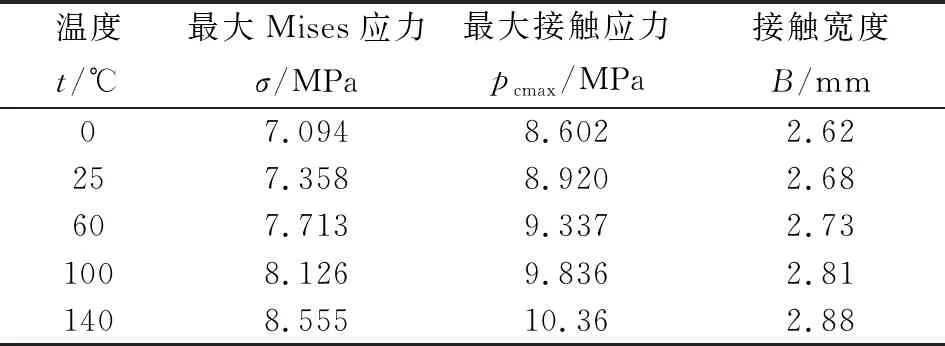
表6 不同环境温度下应力、接触宽度计算结果

橡胶和钢材均会发生热胀冷缩。对于钢材，热膨胀会导致钢材的沟槽深度的增大，等效于预压缩率的减小，因此导致最大接触压力减小；相反，收缩会导致钢材的最大接触压力的增大。对于O形圈，膨胀会增大O形圈与盖板间的接触，等效于预压缩率的增大，导致最大接触压力增大；相反，收缩会导致O形圈的最大接触压力减小。由于O形圈的热膨胀系数(1.15×10-4℃-1)远大于钢材的热膨胀系数(1.15×10-5℃-1)，因此O形圈的温度作用效果占主导地位，即随着温度的提高，最大接触压力逐渐增大。另一方面，最大Mises应力随温度逐渐增大，但始终小于拉伸断裂强度12.8 MPa，因此不会出现断裂失效。

提取不同环境温度下的界面宏观接触压力分布，结果如图10所示。

图10 不同环境温度下接触压力分布

根据表4、表5参数求解不同环境温度下的泄漏率，结果如图11所示。尽管最大接触压力随着温度的提高逐渐增大，但由于油的黏度大幅度下降，导致体积泄漏率随温度逐渐增大。以140 ℃下计算结果为例，如图12所示，宏观接触压力、粗糙峰接触压力、介质压力、泄漏通道平均高度分布形式与图9结果相似。由于宏观接触压力远大于介质压力(高压侧介质压力为0.4 MPa)，因此粗糙峰接触压力分布与宏观接触压力分布基本重合。

图11 体积泄漏率随环境温度变化规律

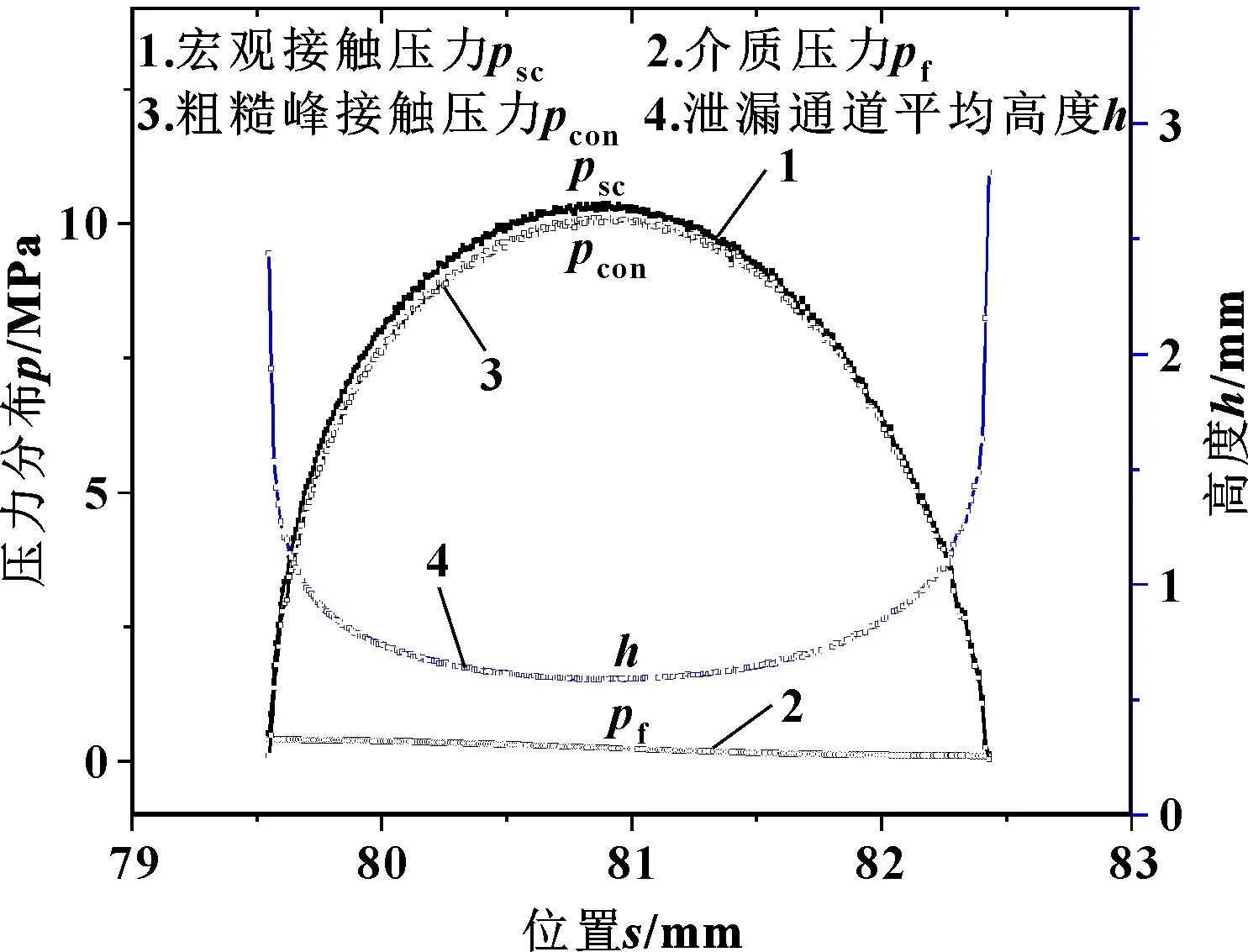
图12 140 ℃下压力、高度分布

2.3 形貌参数的影响

保持高压侧介质压力为0.4 MPa，保持环境温度为25 ℃，设置橡胶表面高度分布标准差分别为1、1.5、2、2.5、3 μm，研究泄漏率与粗糙表面形貌参数的关系，结果如图13、14所示。表面高度分布标准差越大，橡胶表面形貌越粗糙，在相同接触压力作用下，泄漏通道平均高度越大，对应泄漏率越大。

图13 体积泄漏率随表面高度标准差变化规律

图14 泄漏通道平均高度随表面高度标准差变化规律

3 结论

提出了一种基于流固耦合的橡胶O形圈静密封泄漏计算方法。对平行平板泄漏模型进行了改进，进行流体力学分析；采用有限元仿真方法进行固体力学分析；采用GW模型进行接触力学分析。基于上述数值方法，以泄漏率为指标，研究了介质压力、环境温度、表面形貌参数对橡胶O形圈密封性能的影响规律。具体结论如下：

(1)由于橡胶的自紧密封作用，随着介质压力的增大，主密封面的最大接触压力增大，但体积泄漏率逐渐增大；

(2)由于橡胶的热胀冷缩，随着温度的提高，最大接触压力逐渐增大。但由于油的黏度随温度大幅度下降，导致体积泄漏率随温度逐渐增大；

(3)表面高度分布标准差越大，橡胶表面形貌越粗糙，在相同接触压力作用下，泄漏通道平均高度越大，对应泄漏率越大。

与以最大接触压力表征密封性能相比，上述数值方法以泄漏率作为表征密封性能的参数，能综合考虑橡胶的物理、力学性能、表面形貌参数、密封介质参数以及温度、压力等工况对橡胶O形圈密封性能的影响，对橡胶O形圈的寿命预测和失效分析更具指导意义。