柯西积分高阶导数公式的一个注记

陈艳萍

(北京科技大学 数理学院，北京 100083)

1 引 言

众所周知，柯西积分高阶导数公式是复变函数论中的重要公式之一，是由柯西积分公式导出的.二者对深刻学习和研究解析函数都起到了至关重要的作用[1-2].

(1)

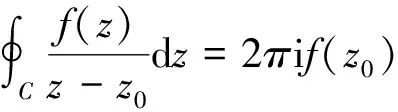
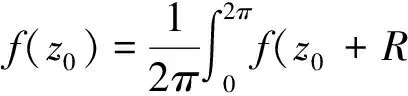
另一方面，在积分号下对z求导，可以推广柯西积分公式，得到柯西积分高阶导数公式的基本形式[3-7]：设函数f(z)在区域D内解析, 则f′(z)仍在区域D内解析, 即解析函数的导数仍为解析函数，且其n阶导数可表示为

其中，C是函数解析域内包含z的任意闭曲线，方向取逆时针方向.

柯西积分高阶导数公式作为研究复变函数论中解析函数的重要工具.它既说明了解析函数的一个重要特征——解析函数的任意阶导数在其解析域内都存在，又得到了解析函数的任意阶导数均可以写成沿区域边界曲线的积分形式.另外，柯西积分高阶导数公式的作用，不仅仅在于用积分表达导数，更体现在通过导数来计算积分.更多地，柯西积分高阶导数公式还可以用来证明刘维尔定理、莫雷拉定理以及柯西不等式等许多重要结果, 具体可参看文献[3-4].因此，关于柯西积分高阶导数公式的研究，无论是对解析函数的理论学习还是其相关应用都具有十分重要的意义.在笔者的研究工作中发现，柯西积分高阶导数公式在调和分析中也有着广泛的应用.该文将以柯西积分高阶导数公式为重要工具，研究调和分析领域中最基本的奇异积分算子——Hilbert变换相关的加权模不等式.

2 预备知识

为了得出主要结果，下面将介绍一些已知的定义和相关引理.

定义1[8](有界线性算子)令(X, ‖·‖X)，(Y, ‖·‖Y)是赋范空间，设T∶D(T)→Y的线性算子，其中D(T)⊂X.那么称算子T是有界的当且仅当存在一个正实数c使得对任意x∈D(T)，

‖Tx‖Y≤c‖x‖X.

定义2[9](L2空间) 设f(x)是上的可测函数，记

并用L2()表示使‖f‖2<∞的f全体，称其为L2空间.

定义3[9](A2函数) 设w(x)是上局部可积的非负函数.则w(x)∈A2，当且仅当对任意的区间Q

定义4[9](L2(w)空间)f(x)是上的可测函数，w(x)是上局部可积的非负函数，记

数据导入SPSS 19.0统计学软件进行统计学分析。所有计量资料均以均数±标准差表示；计数资料[n（%）]采用 χ2检验；两组间的计量资料（±s）采用 t检验，所有统计数据均行双侧检验；P＜0.05为差异有统计学意义。

用L2(w)表示使‖f‖L2(w)<∞的f全体，称其为L2(w)空间.

定义5[10](Hilbert变换) 对任意的f∈L2()，Hilbert变换定义如下：

2007年，Petermichl研究了Hilbert变换的L2(w)有界性[7]，得到下面的结果：

引理1[11]设w∈A2，以及H是Hilbert变换，则存在一个常数γ>0使得

‖H(f)‖L2(w)≤γ[w]A2‖f‖L2(w).

引理2在上，令w(x)=|x|a，则w∈A2当且仅当-1

证考虑Q=[-r,r]即可.那么

当且仅当-1

3 主要结果

定理1设b(x)=log|x|，w(x)=|x|1/2以及H是Hilbert变换，令

则

‖[b,H](f)‖L2(w)≤19γ‖f‖L2(w).

证令ψ(z)f(x)=ezb(x)H(e-zbf)(x)，对ψ(z)求导得

ψ′(z)f(x)=b(x)ezb(x)H(e-zbf)(x)+ezb(x)H(-be-zbf)(x).

根据柯西积分高阶导数公式，得到

令z=δeiθ，θ∈[0,2π]，则

那么利用Minkowski不等式，有

利用欧拉公式

eiθ=cosθ+isinθ，

得到

eδeiθb(x)=eδ(cosθ+isinθ)b(x)=eδcosθ b(x)ei δsinθ b(x).

利用上式，可以得到

令gθ(x)=e-δeiθb(x)f(x)，则

且

(2)

因此需要估计

利用引理1，得到

再利用(2)式得

‖[b,H]f‖L2(w)≤19γ‖f‖L2(w).

4 结 论

本文首先回顾了柯西积分公式和柯西积分高阶导数公式的基本形式，并且给出了它们在复变函数论中关于解析函数的作用.然后以柯西积分高阶导数公式为工具，证明了与Hilbert变换相关的加权模不等式，进一步说明了柯西积分高阶导数公式对于调和分析的理论研究所起到的重要作用.

致谢作者非常感谢审稿专家提出的宝贵意见和相关参考文献对本文的有益启示.