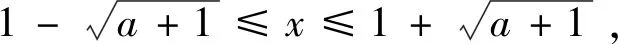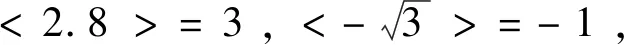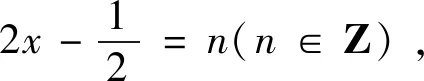基于逻辑推理素养培育的教学实践与思考
厦门大学附属实验中学 (363123) 郑元壮 孟 涛
在一些学生眼中,数学是“高冷”的.数学教学中如果一味机械式的刷题,只会令人感到疲倦、厌烦.其实,数学不仅有推演,更多的时候应该是让学生去品悟、发现,是有“温度”的学科,数学学习需要启迪、质疑和灵感,而这些都需要我们在教学中逐步培育学生的逻辑推理素养.《普通高中数学课程标准(2017)》提出了数学学科六大核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析,这就要求我们教师要转变培养数学思维的教学方式,体现出阅读与品悟比刷题强训更加简洁高效.本文以人教版《数学(必修 第一册)(2019)》函数教学的几个案例,分享笔者的教学实践与思考.
1.借助逻辑推理,促进思维严密性
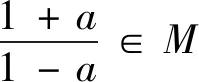
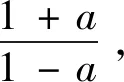
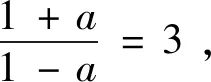
2.借助逻辑思维,揭示数学本质
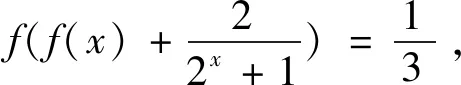
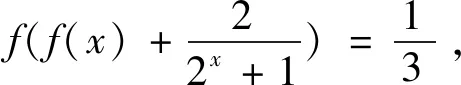
评注:本例初看是一个“抽象函数”的问题,学生一下会显得无所适从,如果学会推理转化,“品读”函数概念和单调性的定义的本质,就会识得“庐山真面目”,进而揭开问题的神秘面纱.可见具备“逻辑推理”素养、扎实的数学功底才是解决问题的“利器”.
3.借助逻辑推理,启发思维创新性
例3 (多项选择题)已知函数f(x)=ex+x-2,g(x)=lnx+x-2,且f(a)=g(b)=0,则下列结论正确的是( ).
A.a>bB.g(a)<0 C.g(a)>0>f(b) D.a+b=2 分析:注意到条件中函数解析式的形式,都含有“x-2”这一特点,而y=ex和y=lnx是比较熟悉的函数,所以思路上应该往函数图象与性质方向考虑.对于A,B,C三个选项都与不等式相关,所以应该从单调性的方向考虑.由于函数y=ex,y=lnx,y=x-2是(0,+∞)上的增函数,所以f(x)=ex+x-2,g(x)=lnx+x-2是(0,+∞)上的增函数.又因为f(0)=-1<0,f(1)=e-1>0,g(1)=-1<0,g(2)=ln2>0,由零点存在定理,所以0 评注:逻辑推理是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.在课堂教学中,教师应把困难的问题直观化、抽象的问题形象化,培养学生的直观想象,增强学生运用图形和空间想象思考问题的意识,引导学生感悟事物的本质,逐步形成创新思维. 例4 (多项选择题)关于x的一元二次不等式x2-2x-a≤0的解集中有且只有5个整数,则实数a的值可以是( ). A.2 B.4 C.6 D.8 评注:本例的难点不是求不等式的解集,而是对条件“解集中有且只有5个整数”感到无法下手,因而,需要把问题转化为解集的区间长度问题.数学思想是数学知识、数学技能、数学方法的本质体现,是形成数学能力的桥梁.提高分析问题和解决问题的能力并形成数学意识,离不开数学思想.本题以一元二次不等式的解为载体,渗透数形结合思想,化归与转化的数学思想. 评注:对于新定义的题型,在高考中屡见不鲜,它不仅考查学生的创新能力,还能检验学生的临场应变能力,要求学生对新信息识别、加工、转化、应用.本例中运用换元思想找到问题的突破口,整个题目就迎刃而解. 如何在教学中落实新课程改革数学核心素养之“逻辑推理”的培育是每一位数学教师都要面临的问题,“核心素养”更加明确了数学教学的目标,需要贯穿在我们的日常教学中,同时也为学生的学习明确了方向.因此在“核心素养”的指导下,课堂教学更要突出“阅读与品悟”的数学逻辑思维培养,这也是数学学科的魅力所在.4.借助逻辑推理,品悟数学思想