固体充填开采中的矸石粒径级配优化试验

肖 博，王宇轩，王梓旭，易 辉

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；2.中国矿业大学(北京) 能源与矿业学院，北京 100083)

固体充填开采是一种以固体混合材料作为充填承压结构的绿色矿山开采技术，其中的骨料多采用各种粒径复合的矸石。矸石属于散粒体材料，其力学性质很大程度上取决于级配特征和母岩性质。对于具体某一矿区而言，矸石母岩性质往往比较固定，此时，矸石的级配特征决定了充填体的压密程度和承压能力。原生矸石级配较差，孔隙率高，利用其进行固体充填时易产生较大的压缩量，导致充填率较低，因此对矸石粒径级配进行优化具有重要的工程指导意义[1-3]。

当矸石及其混合材料进入采空区成为充填体时，水平方向由于受到围岩和支护结构极强的约束作用，几乎不发生变形，垂直方向在上覆岩层的重力作用下，变形较为明显。因此，在侧限近似完全约束且仅有垂直应力作用下，矸石充填体的压实变形特性在固体充填采煤实践中受到更多关注[4-5]。本文将以材料压实变形量、破碎粒径变化程度及模拟试验中充填效果[6-7]作为评价指标，应用理论计算、实验室试验和数值模拟等研究方法对固体充填开采过程中的矸石粒径级配优化展开研究，旨在为固体充填材料配比提供更合理的骨料级配，在进一步提高充填率的同时，降低设计和施工成本。

1 基于泰波理论的试验方案及试验设备

1.1 泰波理论在散体颗粒级配优化方面的应用

由大量文献观察得知，泰波理论在散体颗粒级配优化方面应用较为广泛[8-9]。

式中，P为散体各粒径的通过百分率，%；d为散体中的各粒径，mm；D为散体的最大粒径，mm；n为级配系数。

在泰波理论中，最大粒径D相同时，不同级配系数n可得到不同的粒径配比。

1.2 试验方案

按最大粒径D=50，40，30，20 mm设置4个试验组，每个试验组内按级配系数n=0.3，0.4，0.5，0.6，0.7设置5个人工级配组，并取原始级配(粒径范围和粒径占比分别为50～40 mm，5%；40～30 mm，9%；30～20 mm，12%；20～15 mm，5.4%；15～10 mm，9.6%；10～5 mm，22%；5～0 mm，37%)和平均级配做对照组。粒径级配优化试验方案详见表1。

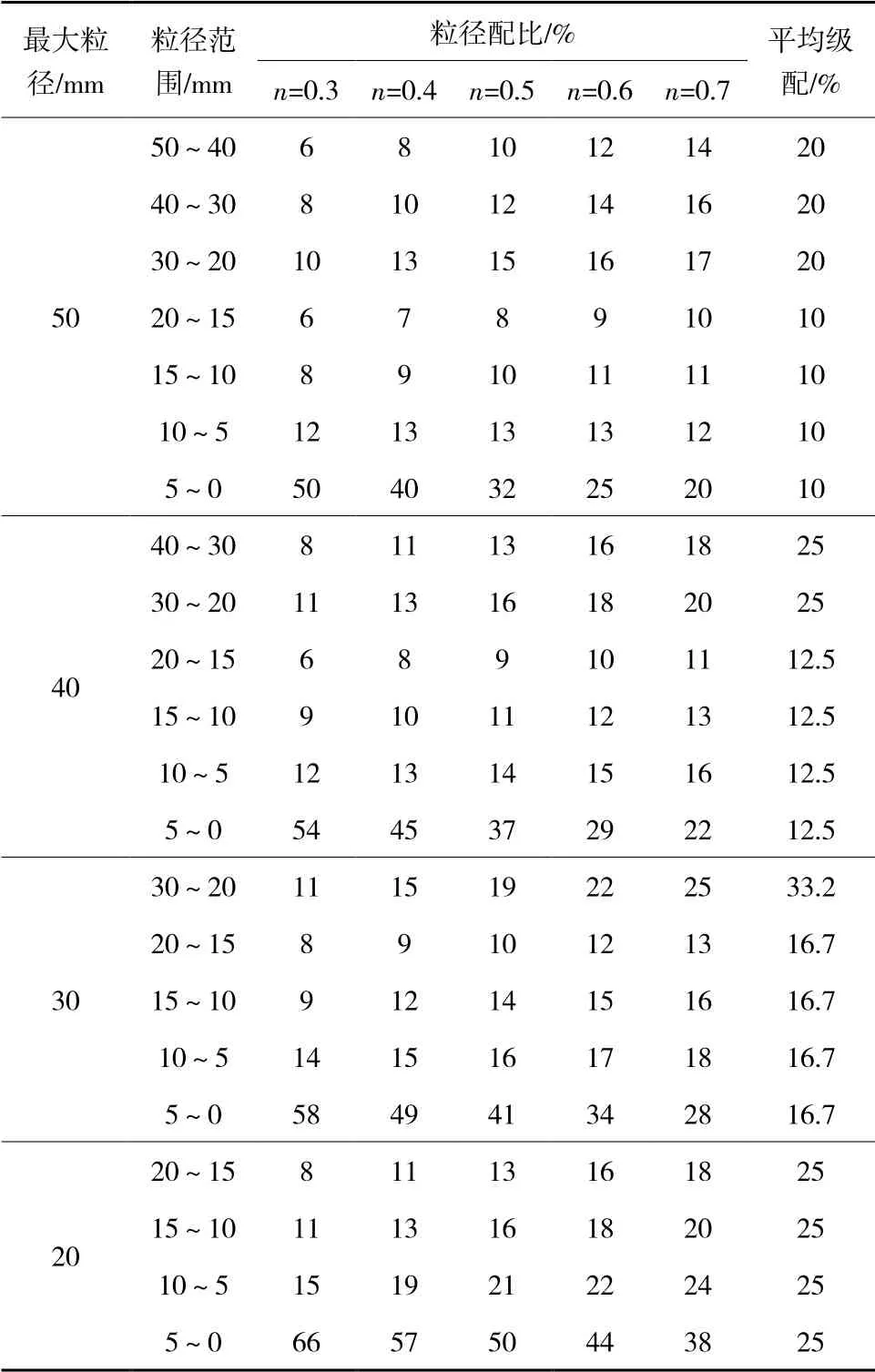
表1 矸石粒径级配优化试验方案Table 1 Optimum test scheme for grading of gangue particle size

考虑到固体充填采煤所配备的液压支架可为充填材料提供2 MPa夯实力，因此可取2 MPa时的压实应变ε作为其中1个指标，另外通过对比最大变形以及破碎前后的粒径分形情况来确定矸石粒径组在不同最大粒径D条件下的最佳级配[10-11]。按照上述方案对各粒径级配组矸石试样进行压实试验，结合实际工作面的埋深和上覆岩层的平均容重，确定最大轴向压应力为10 MPa，试验力加载速率为1 kN/s，每组测试时间3000 s，每4 s记录1次数据。根据压力机记录的数据，分析材料试样在压实过程中的应变和变形模量随应力的变化规律[12]。

1.3 试验设备及材料

拟通过压实试验获得不同级配矸石粒径组的压实变形数据。试验选用YAD-2000微机控制电液伺服压力机，最大载荷为2000 kN。压实钢筒由40号优质碳素结构钢制成，强度较高，不易变形。钢筒内径260 mm，最大装料高度300 mm。试验设备如图1所示。

图1 压力机及压实钢筒Fig.1 Press and compacted steel cylinder

试验材料为各种粒径的矸石，取自鄂尔多斯王家塔煤矿，使用国家标准分级筛挑出大于50 mm的矸石后，将50 mm之内的矸石通过40，30，20，15，10，5 mm等6个次级分级筛进行粒径分组，如图2所示。

图2 不同粒径范围的矸石Fig.2 Gangue with different particle sizes

2 矸石粒径级配优化试验数据分析

2.1 应变随级配系数变化的规律

随着应力的增大，应变呈现出从快速增大到平稳增大再到平缓增大的变化规律。应力在0～2 MPa时，各级配组应变都比较大，占总应变的50%以上。 这说明在此过程中各种级配均易发生变形，是变形的主要阶段；而压应力σ在2～10 MPa过程中，试样变形速度明显减小，变形模量逐渐增大。平均级配组由于大粒径含量多，相较于泰波级配组压实变形量较大，且0～2 MPa内压实变形量占比较小。

由图3可知，当最大粒径D=20 mm时，最大变形量小于原始级配的级配组合有n=0.3，n=0.4和n=0.5，其中n=0.4的变形量最小，在压实过程中最不易发生变形，且0～2 MPa内的压实变形量占总变形量的64.1%，压实变形速度最大。

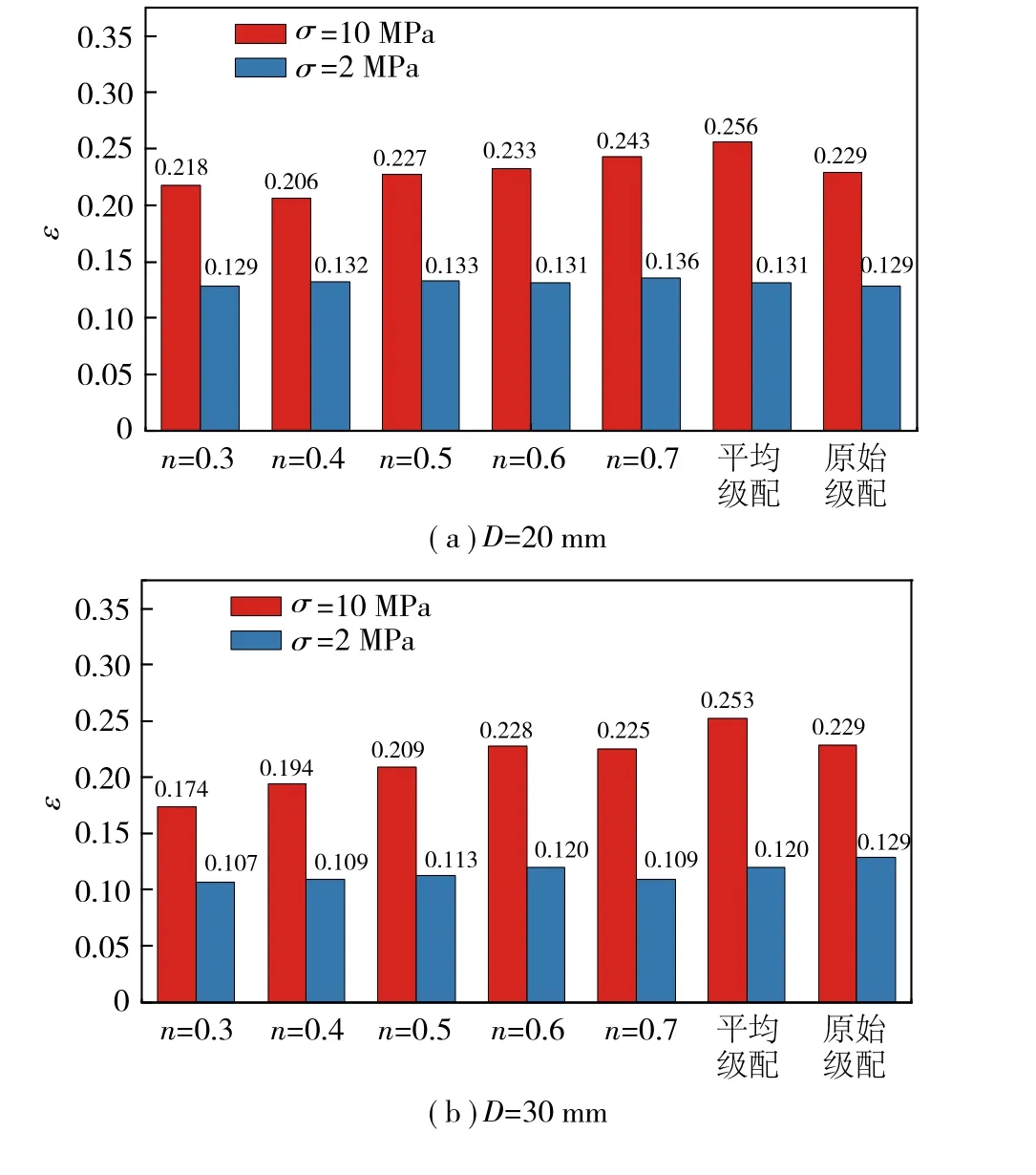
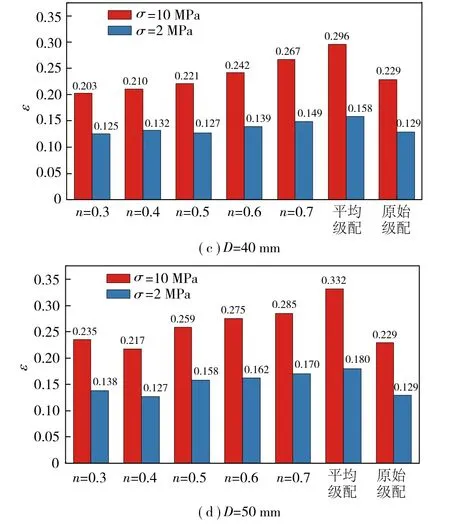
图3 各最大粒径组应变随级配系数变化的规律Fig.3 Variation of strain of each maximum particle size group with gradation coefficient

当D=30 mm时，级配组n=0.3的变形量最小，当σ=2 MPa时，ε=0.107；当σ=10 MPa时，ε=0.174，0～2 MPa内压实变形量占总变形量的61.5%。

当D=40 mm时，级配组n=0.3的变形量最小，σ=2 MPa时，ε=0.125；σ=10 MPa时，ε=0.203；级配组n=0.4在0～2 MPa内压实变形速度最大。

当D=50 mm时，仅n=0.4对应的级配组变形量小于原始级配，且0～2 MPa内压实变形速度最大；σ=2 MPa时，ε=0.127，应力达到最大时，最终应变为0.217。

2.2 压实破碎前后矸石粒径变化规律

在泰波级配中，随着级配系数n值的不断增大，0～5 mm内的粒径含量逐渐减小，5 mm～D范围 内的各级粒径含量逐渐增大，即n值越小，最大粒 径与最小粒径含量之间的差值越小，破碎程度越高。

将压实前后的矸石筛分，然后进行称量和计算，以试验筛孔径的对数大小为横坐标，过筛通过率为纵坐标，在半对数坐标中画出4种最小应变粒径组在压实前后的级配曲线，如图4所示。

4种级配曲线在压实后均较压实前向左上偏移，说明较细的矸石颗粒含量增加，大粒径矸石发生了破碎，且最大粒径越小，颗粒破碎程度越大。级配曲线的倾斜程度可以表征粒径级配优化情况，图4(b)中曲线(D=20 mm，n=0.4)和(D=30 mm，n=0.3) 增长较为平缓，颗粒破碎发展程度较高，更加接近密实状态[13]。

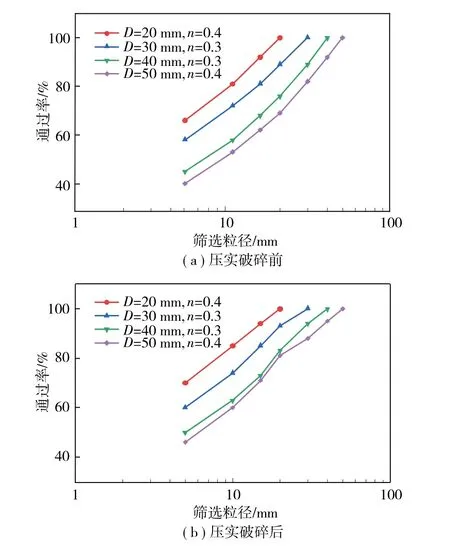
图4 压实破碎前后的级配曲线Fig.4 Grading curves before and after compaction crushing

2.3 变形模量-应力关系曲线

由图5可知，随着压应力σ的不断增大，各级配组压实变形模量E也逐渐增大，与压应力σ呈线性变化关系[4]。

图5 E-σ关系曲线Fig.5 E-σ relationship curves

在E-σ关系曲线中，当D=30 mm，n=0.3，σ= 10 MPa时，最大变形模量为E=57.47 MPa，明显大于其他几种级配，说明同种应力情况下，其压缩变形量最小。

3 基于试验数据的充填体参数优化

为验证优化后的矸石粒径级配在固体充填采煤中的充填效果，采用FLAC3D数值模拟软件对王家塔煤矿3108工作面在推进过程中的应力分布和覆岩移动进行模拟。

充填体变形模量E在压实过程中是变化的，为准确体现充填体的压实效果，需对体积模量K和剪切模量G进行动态赋参。先对图5中的E-σ关系曲 线进行拟合，关系式详见表2。

表2 E-σ拟合关系式Table 2 E-σ fitting relations

体积模量K、剪切模量G与变形模量E之间的关系为

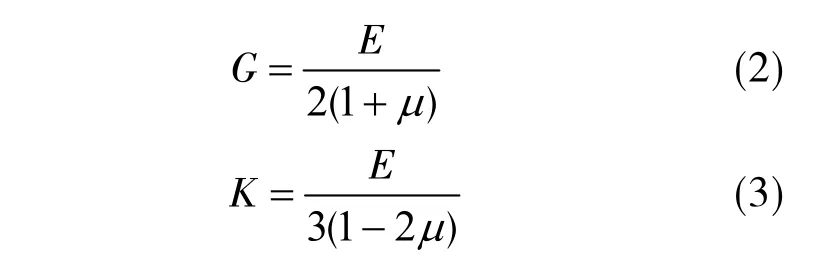
在计算过程中利用FISH程序语言对K与G进行更新：首先获取充填体顶部的垂向应力σ，根据表1中的E-σ拟合关系式计算出E，然后由式(2)和(3)得到G和K的值。计算中取μ=0.3，每计算20个时步重新获取一次σ，并更新各模量数值，依次循环，如此可模拟充填体压实硬化的效应[13-15]。

4 数值模拟下的充填效果分析

4.1 模型建立

对煤层的顶底板岩层进行编号，从下向上依次为直接底、3-1煤、直接顶(1号岩层)、基本顶(2号岩层)和3～6号岩层。

3108工作面煤岩层情况见表3。

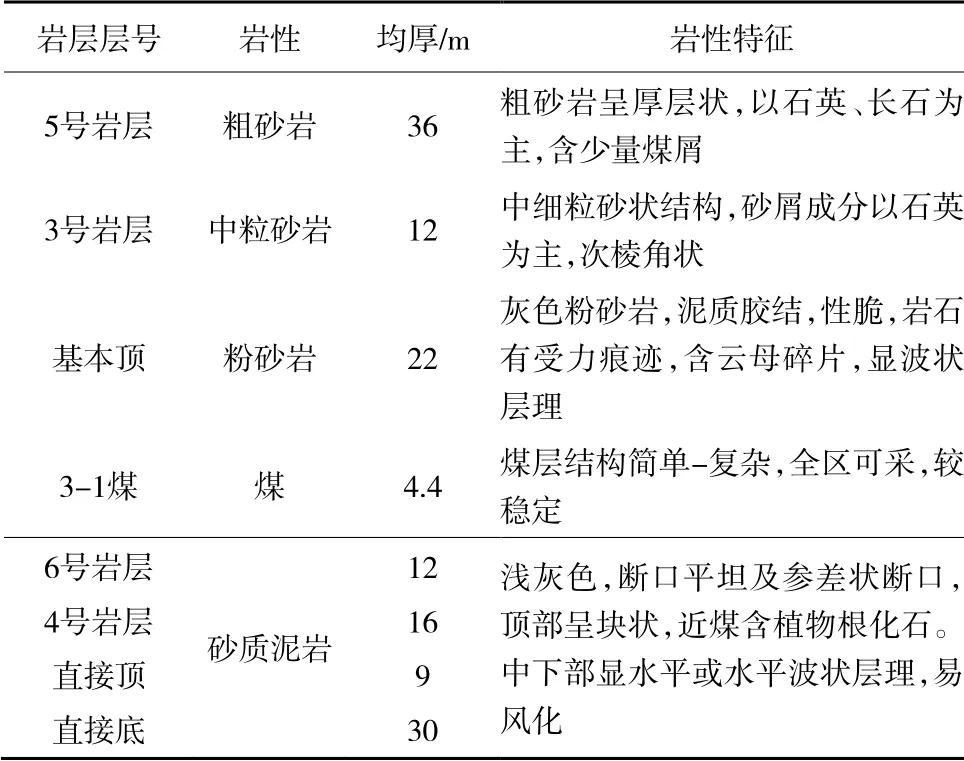
表3 3108工作面煤岩层情况Table 33108 working face coal formation situation

建立几何模型尺寸为：141.4 m×1 m×300 m，如图6所示，数值模拟煤岩层物理力学参数详见表 4。

图6 数值模拟模型Fig.6 Numerical simulation model

表4 煤岩层物理力学参数Table 4 Physical and mechanical parameters of coal strata

4.2 模拟过程

3108工作面采用走向长壁后退式采煤法、大采高综合机械化采煤工艺，可采用固体充填采煤的方法达到控制顶板下沉的目的。工作面主采3-1煤层，煤层倾角平均为2°。为实现采煤与充填并举，进而保证生产效率，工作面需边采边充，从而做到移架、充填工序协调配合。

模拟计算时采用Mohr-Coulomb准则，在x，y和z方向底部施加位移约束边界，上部施加等效于上覆岩层的均布载荷2.95 MPa，初始垂直应力为埋深与容重的乘积，x，y方向的侧压系数分别为1.3，0.8。长壁式固体充填开采模拟采用分步开挖、采一充一的方式，即每次推进10 m之后采用重新赋参的方法对采空区进行充填，然后继续向前开挖10 m，以此类推。充填体部分采用弹性本构模型，左右两侧各留50 m煤柱的前提下，对采空区高度4.18 m内的单元重新赋予矸石充填体动态参数，直接顶下方空余高度为0.22 m，以保证95%的充填率，进而实现充填过程的模拟[16]。

4.3 采场岩层应力分布特征

数值模拟各级配采场岩层应力分布情况如图7所示，在固体充填开采过程中，矸石充填体被逐渐压实，发挥支撑作用的同时能够传递顶底板之间的应力。

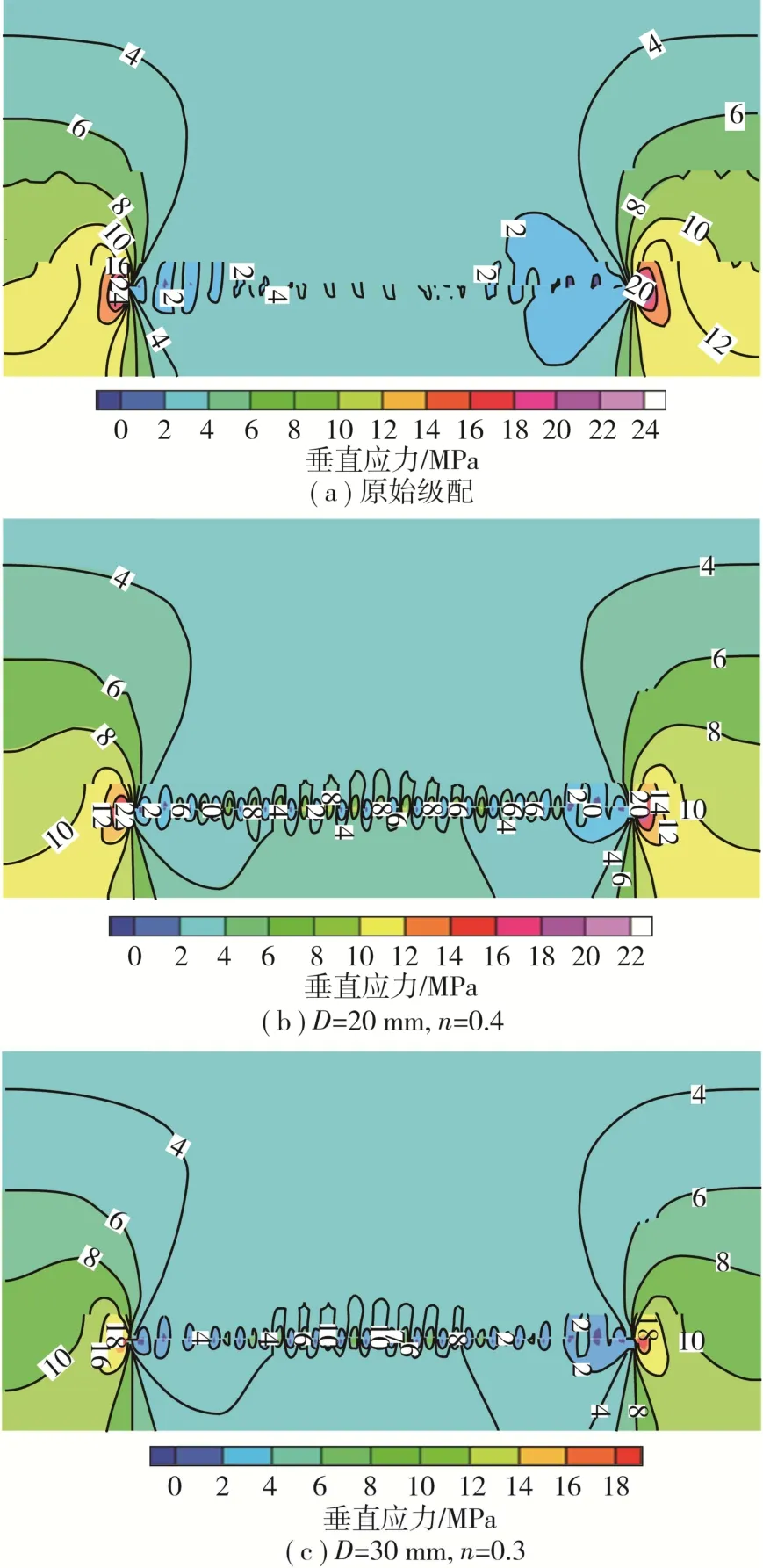
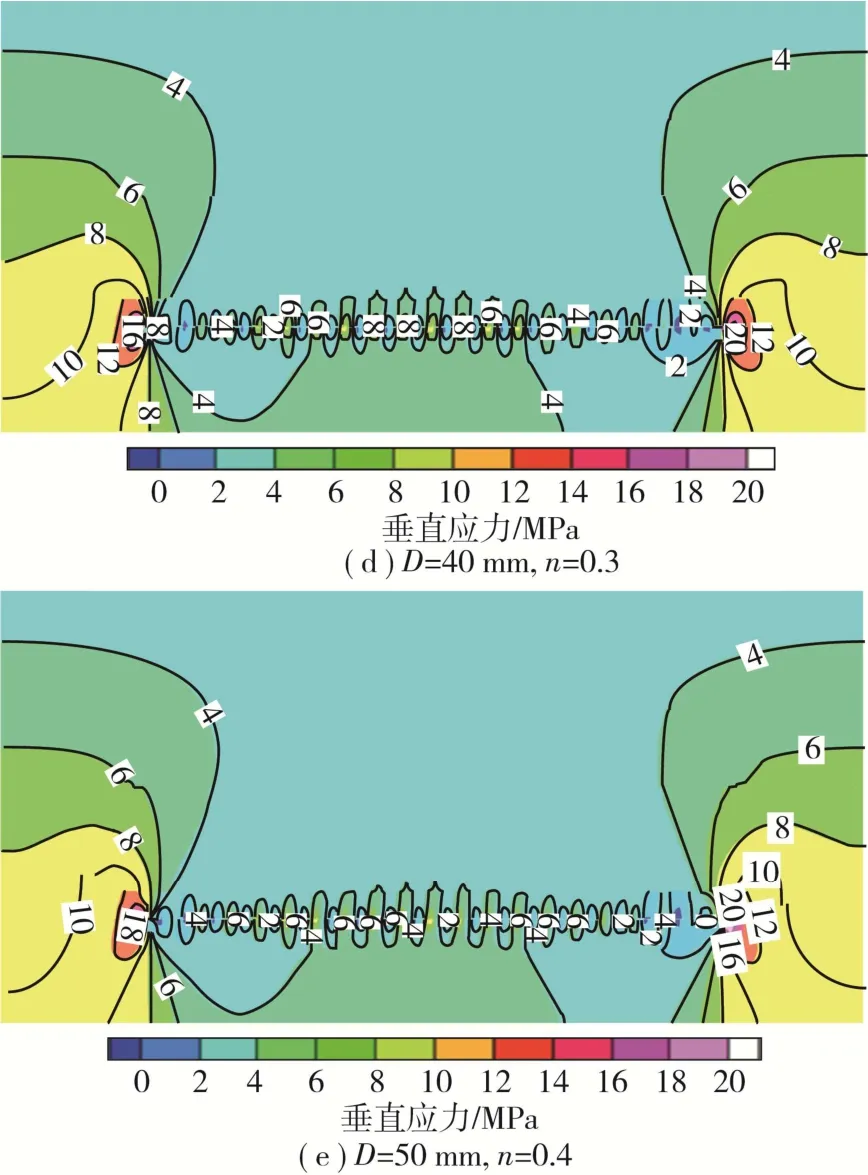
图7 各级配应力分布Fig.7 Distribution of stress at all levels

由图7(a)可知，以原始级配充填时，两侧煤壁应力程度较大，应力峰值为24 MPa，工作面推进过程中，出现大范围低应力区间，充填体承压效果较差，受力峰值仅为4 MPa。由图7(b)～(e)可知，4种优化级配的应力分布具有良好的周期性，两侧煤壁的应力集中程度较小，工作面推进区间内无大范围低应力区。其中，级配组(D=30 mm，n=0.3)对应的充填效果最佳，煤壁处应力峰值降至18 MPa，充填体承压值可达10 MPa，充填体上下应力分布情况一致，说明上覆岩层与底板之间的应力得到充分传递，可为固体充填开采提供更好的围岩应力场[17-18]。

4.4 采场岩层位移分布特征

在固体充填开采技术中，将矸石作为充填材料填入采空区，可以有效控制岩层移动。各采场上覆岩层的垂向变形均有所下沉，呈盆地状，且各处下沉趋势一致，采场中部变形最大，从中部到两头下沉量逐渐变小。由图8可知，4种优化级配的基本顶下沉量明显小于原始级配的基本顶下沉量。其中，D=50 mm，n=0.4级配组对应的下沉量较大，为162 mm；D=20 mm，n=0.4和D=40 mm，n=0.3的下沉量相差较小，接近150 mm，相较于原始级配的182 mm下降约18%；D=30 mm，n=0.3的基本顶下沉量最小，仅有136 mm，相较于原始级配下降25.3%，故能更加有效地控制顶板下沉，为固体充填开采提供更好的围岩位移场[19]。

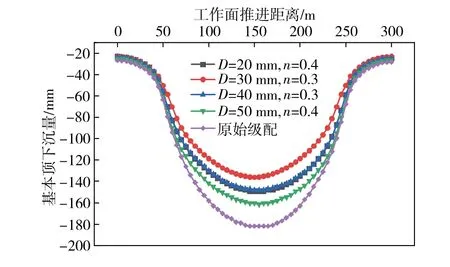
图8 各级配基本顶下沉量Fig.8 Basic top subsidence at all levels

5 矸石破碎成本优化试验

在矸石级配优化试验研究中，对细矸(0～5 mm)的需求量较大，占到矸石总量的50%以上，大幅度增加了矸石的破碎成本。如图9所示，河沙粒径大小与细矸较为接近，而且其含水率比细矸高，若采用河沙替代细矸，不但可以有效降低矸石的破碎成本，还可以提高混合材料的密实程度。

图9 细矸与河沙对比Fig.9 Comparison of fine gangue and river sand

选用变形最小的级配组合，即D=30 mm，n=0.3，将这一组合中的细矸替换成河沙，通过压实试验得到的变形规律如图10所示。

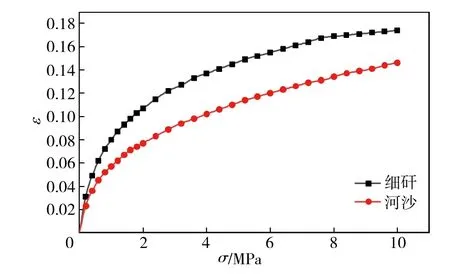
图10 矸石-河沙变形情况Fig.10 Deformation of gangue-river sand

由图10可知，河沙替代细矸情况下，混合材料的整体变形量更小，压密程度更大，在σ=10 MPa时其最终应变ε=0.146，下降16.1%。说明在矸石级配优化和固体充填材料配比过程中，采用河沙代替细矸，可有效降低矸石破碎带来的经济成本。

6 结论

(1) 以泰波理论为基础，按最大粒径D的不同取值设置4个试验组，按级配系数的不同取值在每个试验组内设置6个粒径级配组，并计算了粒径的通过率。

(2) 对矸石粒径级配优化试验数据进行分析，得出4个试验组内压实变形量最小的级配组合，分别为D=20 mm，n=0.4；D=30 mm，n=0.3；D=40 mm，n=0.3和D=50 mm，n=0.4。其中，D=20 mm，n=0.4和D=30 mm，n=0.3压实破碎程度较高，且后者变形模量较大，说明同种压力情况下，D=30 mm，n=0.3级配组的应变最小。

(3) 对E-σ关系曲线进行拟合，得到两者间的线性关系式，结合体积模量K和剪切模量G与变形模量E之间的关系式，得出K，G与σ的变化关系，并在数值模拟计算过程中通过编写FISH程序语言对K与G进行更新，实现了动态赋参。

(4) 分析采场岩层应力分布特征，优化级配的应力分布具有良好的周期性，相较于原始级配，应力集中程度更小，无大范围低应力区。其中，级配组(D=30 mm，n=0.3)对应的充填效果最佳，煤壁处应力峰值降至18 MPa，充填体承压值可达10 MPa。

(5) 分析采场岩层位移分布特征，在固体充填过程中，优化级配的顶板下沉量明显小于原始级配，其中，D=30 mm，n=0.3的基本顶下沉量最小，仅有136 mm，比原始级配下降25.3%。

(6) 在矸石级配优化和固体充填材料配比过程中，可采用河沙代替细矸，提高充填率的同时可有效降低矸石破碎成本。